Vector space
Encyclopedia
A vector space is a mathematical structure
formed by a collection of vectors
: objects that may be added together and multiplied
("scaled") by numbers, called scalars
in this context. Scalars are often taken to be real number
s, but one may also consider vector spaces with scalar multiplication by complex number
s, rational number
s, or even more general fields
instead. The operations of vector addition and scalar multiplication have to satisfy certain requirements, called axiom
s, listed below. An example of a vector space is that of Euclidean vectors which are often used to represent physical
quantities such as force
s: any two forces (of the same type) can be added to yield a third, and the multiplication of a force vector by a real factor is another force vector. In the same vein, but in more geometric
parlance, vectors representing displacements in the plane or in three-dimensional space
also form vector spaces.
Vector spaces are the subject of linear algebra
and are well understood from this point of view, since vector spaces are characterized by their dimension, which, roughly speaking, specifies the number of independent directions in the space. The theory is further enhanced by introducing on a vector space some additional structure, such as a norm
or inner product. Such spaces arise naturally in mathematical analysis
, mainly in the guise of infinite-dimensional function spaces whose vectors are functions
. Analytical problems call for the ability to decide if a sequence of vectors converges
to a given vector. This is accomplished by considering vector spaces with additional data, mostly spaces endowed with a suitable topology
, thus allowing the consideration of proximity and continuity
issues. These topological vector space
s, in particular Banach space
s and Hilbert space
s, have a richer theory.
Historically, the first ideas leading to vector spaces can be traced back as far as 17th century's analytic geometry
, matrices
, systems of linear equation
s, and Euclidean vectors. The modern, more abstract treatment, first formulated by Giuseppe Peano
in the late 19th century, encompasses more general objects than Euclidean space, but much of the theory can be seen as an extension of classical geometric ideas like line
s, planes and their higher-dimensional analogs.
Today, vector spaces are applied throughout mathematics, science
and engineering
. They are the appropriate linear-algebraic notion to deal with systems of linear equations; offer a framework for Fourier expansion
, which is employed in image compression
routines; or provide an environment that can be used for solution techniques for partial differential equation
s. Furthermore, vector spaces furnish an abstract, coordinate-free way of dealing with geometrical and physical objects such as tensor
s. This in turn allows the examination of local properties of manifolds by linearization techniques. Vector spaces may be generalized in several directions, leading to more advanced notions in geometry and abstract algebra
.
s in a fixed plane, starting at one fixed point. This is used in physics to describe force
s or velocities
. Given any two such arrows, v and w, the parallelogram
spanned by these two arrows contains one diagonal arrow that starts at the origin, too. This new arrow is called the sum of the two arrows and is denoted . Another operation that can be done with arrows is scaling: given any positive real number
a, the arrow that has the same direction as v, but is dilated or shrunk by multiplying its length by a, is called multiplication of v by a. It is denoted . When a is negative, is defined as the arrow pointing in the opposite direction, instead.
The following shows a few examples: if a = 2, the resulting vector has the same direction as w, but is stretched to the double length of w (right image below). Equivalently 2 · w is the sum . Moreover, (−1) · v = −v has the opposite direction and the same length as v (blue vector pointing down in the right image).
.) Such a pair is written as (x, y). The sum of two such pairs and multiplication of a pair with a number is defined as follows: + (x2, y2) = (x1 + x2, y1 + y2)
and
F is a set V together with two binary operators
that satisfy the eight axioms listed below. Elements of V are called vectors. Elements of F are called scalars. In this article, vectors are differentiated from scalars by boldface.It is also common, especially in physics, to denote vectors with an arrow on top: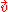
. In the two examples above, our set consists of the planar arrows with fixed starting point and of pairs of real numbers, respectively, while our field is the real numbers. The first operation, vector addition, takes any two vectors v and w and assigns to them a third vector which is commonly written as and called the sum of these two vectors. The second operation takes any scalar a and any vector v and gives another . In view of the first example, where the multiplication is done by rescaling the vector v by a scalar a, the multiplication is called scalar multiplication
of v by a.
To qualify as a vector space, the set V and the operations of addition and multiplication have to adhere to a number of requirements called axiom
s. In the list below, let u, v, w be arbitrary vectors in V, and a, b be scalars in F.
These axioms generalize properties of the vectors introduced in the above examples. Indeed, the result of addition of two ordered pairs (as in the second example above) does not depend on the order of the summands: + (xw, yw) = (xw, yw) + (xv, yv),
Likewise, in the geometric example of vectors as arrows, v + w = w + v, since the parallelogram defining the sum of the vectors is independent of the order of the vectors. All other axioms can be checked in a similar manner in both examples. Thus, by disregarding the concrete nature of the particular type of vectors, the definition incorporates these two and many more examples in one notion of vector space.
Subtraction of two vectors and division by a (non-zero) scalar can be performed via
The concept introduced above is called a real vector space. The word "real" refers to the fact that vectors can be multiplied by real number
s, as opposed to, say, complex number
s. When scalar multiplication is defined for complex numbers, the denomination complex vector space is used. These two cases are the ones used most often in engineering. The most general definition of a vector space allows scalars to be elements of a fixed field
F. Then, the notion is known as F-vector spaces or vector spaces over F. A field is, essentially, a set of numbers possessing addition
, subtraction
, multiplication
and division
operations.Some authors (such as ) restrict attention to the fields R or C, but most of the theory is unchanged over an arbitrary field. For example, rational number
s also form a field.
In contrast to the intuition stemming from vectors in the plane and higher-dimensional cases, there is, in general vector spaces, no notion of nearness, angle
s or distance
s. To deal with such matters, particular types of vector spaces are introduced; see below.
: that u + v and av are in V for all a in F, and u, v in V. Some older sources mention these properties as separate axioms.
In the parlance of abstract algebra
, the first four axioms can be subsumed by requiring the set of vectors to be an abelian group
under addition. The remaining axioms give this group an F-module
structure. In other words there is a ring homomorphism
ƒ from the field F into the endomorphism ring
of the group of vectors. Then scalar multiplication av is defined as (ƒ(a))(v).
There are a number of direct consequences of the vector space axioms. Some of them derive from elementary group theory, applied to the additive group of vectors: for example the zero vector 0 of V and the additive inverse −v of any vector v are unique. Other properties follow from the distributive law, for example av equals 0 if and only if a equals 0 or v equals 0.
, via the introduction of coordinates in the plane or three-dimensional space. Around 1636, Descartes
and Fermat
founded analytic geometry
by equating solutions to an equation of two variables with points on a plane curve
. To achieve geometric solutions without using coordinates, Bolzano introduced, in 1804, certain operations on points, lines and planes, which are predecessors of vectors. This work was made use of in the conception of barycentric coordinates
by Möbius
in 1827. The foundation of the definition of vectors was Bellavitis
' notion of the bipoint, an oriented segment one of whose ends is the origin and the other one a target. Vectors were reconsidered with the presentation of complex numbers by Argand
and Hamilton
and the inception of quaternion
s and biquaternions by the latter. They are elements in R2, R4, and R8; treating them using linear combination
s goes back to Laguerre in 1867, who also defined systems of linear equations.
In 1857, Cayley
introduced the matrix notation which allows for a harmonization and simplification of linear maps. Around the same time, Grassmann studied the barycentric calculus initiated by Möbius. He envisaged sets of abstract objects endowed with operations. In his work, the concepts of linear independence
and dimension
, as well as scalar products are present. Actually Grassmann's 1844 work exceeds the framework of vector spaces, since his considering multiplication, too, led him to what are today called algebra
s. Peano was the first to give the modern definition of vector spaces and linear maps in 1888.
An important development of vector spaces is due to the construction of function spaces by Lebesgue
. This was later formalized by Banach
and Hilbert
, around 1920. At that time, algebra
and the new field of functional analysis
began to interact, notably with key concepts such as spaces of p-integrable functions
and Hilbert space
s. Vector spaces, including infinite-dimensional ones, then became a firmly established notion, and many mathematical branches started making use of this concept.
whose elements are n-tuples
(sequences of length n):, where the ai are elements of F.
The case F = R and n = 2 was discussed in the introduction above. Infinite coordinate sequences, and more generally functions from any fixed set Ω to a field F also form vector spaces, by performing addition and scalar multiplication pointwise. That is, the sum of two functions ƒ and g is given by(w) = ƒ(w) + g(w)
and similarly for multiplication. Such function space
s occur in many geometric situations, when Ω is the real line
or an interval
, or other subset
s of Rn. Many notions in topology and analysis, such as continuity
, integrability
or differentiability are well-behaved with respect to linearity: sums and scalar multiples of functions possessing such a property still have that property. Therefore, the set of such functions are vector spaces. They are studied in greater detail using the methods of functional analysis
, see below. Algebraic constraints also yield vector spaces: the vector space F[x
] is given by polynomial functions:
are given by triples with arbitrary a, b = a/2, and c = −5a/2. They form a vector space: sums and scalar multiples of such triples still satisfy the same ratios of the three variables; thus they are solutions, too. Matrices
can be used to condense multiple linear equations as above into one vector equation, namely
where A =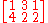
is the matrix containing the coefficients of the given equations, x is the vector Ax denotes the matrix product and 0 = (0, 0) is the zero vector. In a similar vein, the solutions of homogeneous linear differential equations form vector spaces. For example
yields ƒ(x) = a e−x + bx e−x, where a and b are arbitrary constants, and ex is the natural exponential function.
s F / E ("F over E") provide another class of examples of vector spaces, particularly in algebra and algebraic number theory
: a field F containing a smaller field E becomes an E-vector space, by the given multiplication and addition operations of F. For example the complex numbers are a vector space over R. A particularly interesting type of field extension in number theory
is Q(α), the extension of the rational numbers Q by a fixed complex number α. Q(α) is the smallest field containing the rationals and a fixed complex number α. Its dimension as a vector space over Q depends on the choice of α.
I that spans the whole space, and is minimal with this property. The former means that any vector v can be expressed as a finite sum (called linear combination
) of the basis elements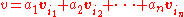
,
where the ak are scalars and vik (k = 1, ..., n) elements of the basis B. Minimality, on the other hand, is made formal by requiring B to be linearly independent. A set of vectors is said to be linearly independent if none of its elements can be expressed as a linear combination of the remaining ones. Equivalently, an equation
can only hold if all scalars a1, ..., an equal zero. Linear independence ensures that the representation of any vector in terms of basis vectors, the existence of which is guaranteed by the requirement that the basis span V, is unique. This is referred to as the coordinatized viewpoint of vector spaces, by viewing basis vectors as generalizations of coordinate vectors x, y, z in R3 and similarly in higher-dimensional cases.
The coordinate vector
s e1 = (1, 0, ..., 0), e2 = (0, 1, 0, ..., 0), to en = (0, 0, ..., 0, 1), form a basis of Fn, called the standard basis
, since any vector (x1, x2, ..., xn) can be uniquely expressed as a linear combination of these vectors: = x1(1, 0, ..., 0) + x2(0, 1, 0, ..., 0) + ... + xn(0, ..., 0, 1) = x1e1 + x2e2 + ... + xnen.
Every vector space has a basis. This follows from Zorn's lemma
, an equivalent formulation of the axiom of choice. Given the other axioms of Zermelo-Fraenkel set theory, the existence of bases is equivalent to the axiom of choice. The ultrafilter lemma, which is weaker than the axiom of choice, implies that all bases of a given vector space have the same number of elements, or cardinality. It is called the dimension of the vector space, denoted dim V. If the space is spanned by finitely many vectors, the above statements can be proven without such fundamental input from set theory.
The dimension of the coordinate space Fn is n, by the basis exhibited above. The dimension of the polynomial ring F[x] introduced above is countably infinite, a basis is given by 1, x, x2, ... A fortiori, the dimension of more general function spaces, such as the space of functions on some (bounded or unbounded) interval, is infinite.The indicator functions of intervals (of which there are infinitely many) are linearly independent, for example. Under suitable regularity assumptions on the coefficients involved, the dimension of the solution space of a homogeneous ordinary differential equation
equals the degree of the equation. For example, the solution space for the above equation is generated by e−x and xe−x. These two functions are linearly independent over R, so the dimension of this space is two, as is the degree of the equation.
The dimension (or degree) of the field extension Q(α) over Q depends on α. If α satisfies some polynomial equation
("α is algebraic
"), the dimension is finite. More precisely, it equals the degree of the minimal polynomial
having α as a root. For example, the complex numbers C are a two-dimensional real vector space, generated by 1 and the imaginary unit
i. The latter satisfies i2 + 1 = 0, an equation of degree two. Thus, C is a two-dimensional R-vector space (and, as any field, one-dimensional as a vector space over itself, C). If α is not algebraic, the dimension of Q(α) over Q is infinite. For instance, for α = π
there is no such equation, in other words π is transcendental
.
that reflect the vector space structure—i.e., they preserve sums and scalar multiplication:
An isomorphism
is a linear map such that there exists an inverse map , which is a map such that the two possible compositions
and are identity maps
. Equivalently, ƒ is both one-to-one (injective) and onto (surjective). If there exists an isomorphism between V and W, the two spaces are said to be isomorphic; they are then essentially identical as vector spaces, since all identities holding in V are, via ƒ, transported to similar ones in W, and vice versa via g.
For example, the vector spaces in the introduction are isomorphic: a planar arrow v departing at the origin
of some (fixed) coordinate system
can be expressed as an ordered pair by considering the x- and y-component of the arrow, as shown in the image at the right. Conversely, given a pair (x, y), the arrow going by x to the right (or to the left, if x is negative), and y up (down, if y is negative) turns back the arrow v.
Linear maps V → W between two fixed vector spaces form a vector space HomF(V, W), also denoted L(V, W). The space of linear maps from V to F is called the dual vector space, denoted V∗. Via the injective natural map V → V∗∗, any vector space can be embedded into its bidual; the map is an isomorphism if and only if the space is finite-dimensional.
Once a basis of V is chosen, linear maps are completely determined by specifying the images of the basis vectors, because any element of V is expressed uniquely as a linear combination of them. If dim V = dim W, a 1-to-1 correspondence
between fixed bases of V and W gives rise to a linear map that maps any basis element of V to the corresponding basis element of W. It is an isomorphism, by its very definition. Therefore, two vector spaces are isomorphic if their dimensions agree and vice versa. Another way to express this is that any vector space is completely classified (up to
isomorphism) by its dimension, a single number. In particular, any n-dimensional F-vector space V is isomorphic to Fn. There is, however, no "canonical" or preferred isomorphism; actually an isomorphism is equivalent to the choice of a basis of V, by mapping the standard basis of Fn to V, via φ. Appending an automorphism
, i.e. an isomorphism yields another isomorphism , the composition
of ψ and φ, and therefore a different basis of V. The freedom of choosing a convenient basis is particularly useful in the infinite-dimensional context, see below.
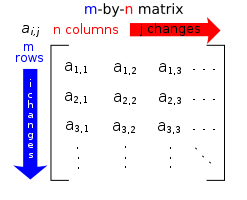Matrices are a useful notion to encode linear maps. They are written as a rectangular array of scalars as in the image at the right. Any m-by-n matrix A gives rise to a linear map from Fn to Fm, by the following
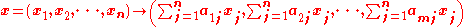, where 
denotes summation
,
or, using the matrix multiplication
of the matrix A with the coordinate vector x:
Moreover, after choosing bases of V and W, any linear map is uniquely represented by a matrix via this assignment.
The determinant
det (A) of a square matrix A is a scalar that tells whether the associated map is an isomorphism or not: to be so it is sufficient and necessary that the determinant is nonzero. The linear transformation of Rn corresponding to a real n-by-n matrix is orientation preserving
if and only if the determinant is positive.
s, linear maps , are particularly important since in this case vectors v can be compared with their image under ƒ, ƒ(v). Any nonzero vector v satisfying λv = ƒ(v), where λ is a scalar, is called an eigenvector of ƒ with eigenvalue λ.The nomenclature derives from German
"eigen", which means own or proper. Equivalently, v is an element of the kernel of the difference (where Id is the identity map
If V is finite-dimensional, this can be rephrased using determinants: ƒ having eigenvalue λ is equivalent to
By spelling out the definition of the determinant, the expression on the left hand side can be seen to be a polynomial function in λ, called the characteristic polynomial
of ƒ. If the field F is large enough to contain a zero of this polynomial (which automatically happens for F algebraically closed
, such as F = C) any linear map has at least one eigenvector. The vector space V may or may not possess an eigenbasis, a basis consisting of eigenvectors. This phenomenon is governed by the Jordan canonical form of the map.. See also Jordan–Chevalley decomposition. The set of all eigenvectors corresponding to a particular eigenvalue of ƒ forms a vector space known as the eigenspace corresponding to the eigenvalue (and ƒ) in question. To achieve the spectral theorem
, the corresponding statement in the infinite-dimensional case, the machinery of functional analysis is needed, see below.
, which determine an object X by specifying the linear maps from X to any other vector space.
W of a vector space V that is closed under addition and scalar multiplication (and therefore contains the 0-vector of V) is called a subspace of V. Subspaces of V are vector spaces (over the same field) in their own right. The intersection of all subspaces containing a given set S of vectors is called its span
, and is the smallest subspace of V containing the set S. Expressed in terms of elements, the span is the subspace consisting of all the linear combination
s of elements of S.
The counterpart to subspaces are quotient vector spaces. Given any subspace W ⊂ V, the quotient space V/W ("V modulo
W") is defined as follows: as a set, it consists of v + W = {v + w, w ∈ W}, where v is an arbitrary vector in V. The sum of two such elements v1 + W and v2 + W is and scalar multiplication is given by a · (v + W) = (a · v) + W. The key point in this definition is that v1 + W = v2 + W if and only if
the difference of v1 and v2 lies in W.Some authors (such as ) choose to start with this equivalence relation
and derive the concrete shape of V/W from this. This way, the quotient space "forgets" information that is contained in the subspace W.
The kernel
ker(ƒ) of a linear map ƒ: V → W consists of vectors v that are mapped to 0 in W. Both kernel and image
im(ƒ) = {ƒ(v), v ∈ V} are subspaces of V and W, respectively. The existence of kernels and images is part of the statement that the category of vector spaces
(over a fixed field F) is an abelian category
, i.e. a corpus of mathematical objects and structure-preserving maps between them (a category
) that behaves much like the category of abelian groups
. Because of this, many statements such as the first isomorphism theorem (also called rank-nullity theorem
in matrix-related terms)
and the second and third isomorphism theorem can be formulated and proven in a way very similar to the corresponding statements for groups
.
An important example is the kernel of a linear map x ↦ Ax for some fixed matrix A, as above. The kernel of this map is the subspace of vectors x such that Ax = 0, which is precisely the set of solutions to the system of homogeneous linear equations belonging to A. This concept also extends to linear differential equations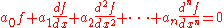
, where the coefficients ai are functions in x, too.
In the corresponding map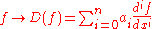
,
the derivative
s of the function ƒ appear linearly (as opposed to ƒ' = ƒ' + g ' and (c·ƒ)' = c·ƒ' for a constant c) this assignment is linear, called a linear differential operator. In particular, the solutions to the differential equation D(ƒ) = 0 form a vector space (over R or C).
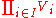of a family of vector spaces Vi consists of the set of all tuples (vi)i ∈ I, which specify for each index i in some index set
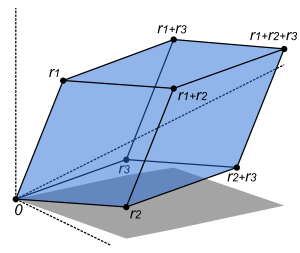
I an element vi of Vi. Addition and scalar multiplication is performed componentwise. A variant of this construction is the direct sum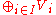
(also called coproduct
and denoted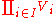
), where only tuples with finitely many nonzero vectors are allowed. If the index set I is finite, the two constructions agree, but differ otherwise.
which deals with extending notions such as linear maps to several variables. A map is called bilinear if g is linear in both variables v and w. That is to say, for fixed w the map is linear in the sense above and likewise for fixed v.
The tensor product is a particular vector space that is a universal recipient of bilinear maps g, as follows. It is defined as the vector space consisting of finite (formal) sums of symbols called tensor
s
subject to the rules
These rules ensure that the map ƒ from the V × W to V ⊗ W that maps a tuple
(v, w) to is bilinear. The universality states that given any vector space X and any bilinear map there exists a unique map u, shown in the diagram with a dotted arrow, whose composition
with ƒ equals g: u(v ⊗ w) = g(v, w). This is called the universal property
of the tensor product, an instance of the method—much used in advanced abstract algebra—to indirectly define objects by specifying maps from or to this object.
to another function. Likewise, linear algebra is not adapted to deal with infinite series, since the addition operation allows only finitely many terms to be added. Therefore, the needs of functional analysis
require considering additional structures. Much the same way the axiomatic treatment of vector spaces reveals their essential algebraic features, studying vector spaces with additional data abstractly turns out to be advantageous, too.
A first example of an additional datum is an order
≤, a token by which vectors can be compared. For example, n-dimensional real space Rn can be ordered by comparing its vectors componentwise. Ordered vector space
s, for example Riesz space
s, are fundamental to Lebesgue integration
, which relies on the ability to express a function as a difference of two positive functions
where ƒ+ denotes the positive part of ƒ and ƒ− the negative part.
, a datum which measures lengths of vectors, or by an inner product, which measures angles between vectors. Norms and inner products are denoted
and 
, respectively. The datum of an inner product entails that lengths of vectors can be defined too, by defining the associated norm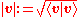 
. Vector spaces endowed with such data are known as normed vector spaces and inner product spaces, respectively.
Coordinate space Fn can be equipped with the standard dot product
:
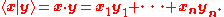
In R2, this reflects the common notion of the angle between two vectors x and y, by the law of cosines
:
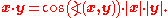
Because of this, two vectors satisfying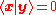
are called orthogonal. An important variant of the standard dot product is used in Minkowski space
: R4 endowed with the Lorentz product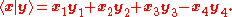
In contrast to the standard dot product, it is not positive definite: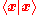
also takes negative values, for example for x = (0, 0, 0, 1). Singling out the fourth coordinate—corresponding to time, as opposed to three space-dimensions—makes it useful for the mathematical treatment of special relativity
.
, a structure that allows one to talk about elements being close to each other. Compatible here means that addition and scalar multiplication have to be continuous maps. Roughly, if x and y in V, and a in F vary by a bounded amount, then so do x + y and ax.This requirement implies that the topology gives rise to a uniform structure, To make sense of specifying the amount a scalar changes, the field F also has to carry a topology in this context; a common choice are the reals or the complex numbers.
In such topological vector spaces one can consider series
of vectors. The infinite sum
denotes the limit
of the corresponding finite partial sums of the sequence (ƒi)i∈N of elements of V. For example, the ƒi could be (real or complex) functions belonging to some function space
V, in which case the series is a function series
. The mode of convergence
of the series depends on the topology imposed on the function space. In such cases, pointwise convergence
and uniform convergence are two prominent examples.
A way to ensure the existence of limits of certain infinite series is to restrict attention to spaces where any Cauchy sequence
has a limit; such a vector space is called complete. Roughly, a vector space is complete provided that it contains all necessary limits. For example, the vector space of polynomials on the unit interval [0,1], equipped with the topology of uniform convergence is not complete because any continuous function on [0,1] can be uniformly approximated by a sequence of polynomials, by the Weierstrass approximation theorem. In contrast, the space of all continuous functions on [0,1] with the same topology is complete. A norm gives rise to a topology by defining that a sequence of vectors vn converges to v if and only if
Banach and Hilbert spaces are complete topological spaces whose topologies are given, respectively, by a norm and an inner product. Their study—a key piece of functional analysis
—focusses on infinite-dimensional vector spaces, since all norms on finite-dimensional topological vector spaces give rise to the same notion of convergence. The image at the right shows the equivalence of the 1-norm and ∞-norm on R2: as the unit "balls" enclose each other, a sequence converges to zero in one norm if and only if it so does in the other norm. In the infinite-dimensional case, however, there will generally be inequivalent topologies, which makes the study of topological vector spaces richer than that of vector spaces without additional data.
From a conceptual point of view, all notions related to topological vector spaces should match the topology. For example, instead of considering all linear maps (also called functional
s) V → W, maps between topological vector spaces are required to be continuous. In particular, the (topological) dual space V∗ consists of continuous functionals V → R (or C). The fundamental Hahn–Banach theorem
is concerned with separating subspaces of appropriate topological vector spaces by continuous functionals.
, are complete normed vector spaces. A first example is the vector space ℓ p
consisting of infinite vectors with real entries x = (x1, x2, ...) whose p-norm given by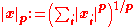
for p < ∞ and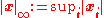 
is finite. The topologies on the infinite-dimensional space ℓ p are inequivalent for different p. E.g. the sequence of vectors xn = (2−n, 2−n, ..., 2−n, 0, 0, ...), i.e. the first 2n components are 2−n, the following ones are 0, converges to the zero vector for p = ∞, but does not for p = 1: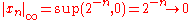
, but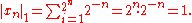 
More generally than sequences of real numbers, functions ƒ: Ω → R are endowed with a norm that replaces the above sum by the Lebesgue integral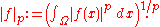
The space of integrable functions on a given domain
Ω (for example an interval) satisfying |ƒ|p < ∞, and equipped with this norm are called Lebesgue spaces
, denoted Lp(Ω).The triangle inequality for |−|p is provided by the Minkowski inequality
. For technical reasons, in the context of functions one has to identify functions that agree almost everywhere
to get a norm, and not only a seminorm. These spaces are complete. (If one uses the Riemann integral
instead, the space is not complete, which may be seen as a justification for Lebesgue's integration theory."Many functions in L2 of Lebesgue measure, being unbounded, cannot be integrated with the classical Riemann integral. So spaces of Riemann integrable functions would not be complete in the L2 norm, and the orthogonal decomposition would not apply to them. This shows one of the advantages of Lebesgue integration.", ) Concretely this means that for any sequence of Lebesgue-integrable functions with |ƒn|p < ∞, satisfying the condition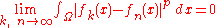
there exists a function ƒ(x) belonging to the vector space Lp(Ω) such that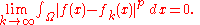
Imposing boundedness conditions not only on the function, but also on its derivative
s leads to Sobolev space
s.
.
The Hilbert space L2(Ω), with inner product given by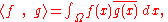
where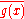
denotes the complex conjugate
of g(x).For p ≠2, Lp(Ω) is not a Hilbert space. is a key case.
By definition, in a Hilbert space any Cauchy sequences converges to a limit. Conversely, finding a sequence of functions ƒn with desirable properties that approximates a given limit function, is equally crucial. Early analysis, in the guise of the Taylor approximation, established an approximation of differentiable function
s ƒ by polynomials. By the Stone–Weierstrass theorem, every continuous function on can be approximated as closely as desired by a polynomial. A similar approximation technique by trigonometric function
s is commonly called Fourier expansion, and is much applied in engineering, see below. More generally, and more conceptually, the theorem yields a simple description of what "basic functions", or, in abstract Hilbert spaces, what basic vectors suffice to generate a Hilbert space H, in the sense that the closure
of their span (i.e., finite linear combinations and limits of those) is the whole space. Such a set of functions is called a basis of H, its cardinality is known as the Hilbert dimension.A basis of a Hilbert space is not the same thing as a basis in the sense of linear algebra above. For distinction, the latter is then called a Hamel basis. Not only does the theorem exhibit suitable basis functions as sufficient for approximation purposes, together with the Gram-Schmidt process it also allows to construct a basis of orthogonal vectors
. Such orthogonal bases are the Hilbert space generalization of the coordinate axes in finite-dimensional Euclidean space
.
The solutions to various differential equation
s can be interpreted in terms of Hilbert spaces. For example, a great many fields in physics and engineering lead to such equations and frequently solutions with particular physical properties are used as basis functions, often orthogonal. As an example from physics, the time-dependent Schrödinger equation
in quantum mechanics
describes the change of physical properties in time, by means of a partial differential equation
whose solutions are called wavefunction
s. Definite values for physical properties such as energy, or momentum, correspond to eigenvalues of a certain (linear) differential operator
and the associated wavefunctions are called eigenstates. The spectral theorem
decomposes a linear compact operator
acting on functions in terms of these eigenfunctions and their eigenvalues.
General vector spaces do not possess a multiplication between vectors. A vector space equipped with an additional bilinear operator
defining the multiplication of two vectors is an algebra over a field. Many algebras stem from functions on some geometrical object: since functions with values in a field can be multiplied, these entities form algebras. The Stone–Weierstrass theorem mentioned above, for example, relies on Banach algebra
s which are both Banach spaces and algebras.
Commutative algebra
makes great use of rings of polynomials
in one or several variables, introduced above. Their multiplication is both commutative and associative. These rings and their quotients
form the basis of algebraic geometry
, because they are rings of functions of algebraic geometric objects.
Another crucial example are Lie algebras, which are neither commutative nor associative, but the failure to be so is limited by the constraints ([x, y] denotes the product of x and y):
), and 0}} (Jacobi identity
).
Examples include the vector space of n-by-n matrices, with [x, y] = xy − yx, the commutator
of two matrices, and R3, endowed with the cross product
.
The tensor algebra
T(V) is a formal way of adding products to any vector space V to obtain an algebra. As a vector space, it is spanned by symbols, called simple tensor
s
The multiplication is given by concatenating such symbols, imposing the distributive law under addition, and requiring that scalar multiplication commute with the tensor product ⊗, much the same way as with the tensor product of two vector spaces introduced above. In general, there are no relations between and . Forcing two such elements to be equal leads to the symmetric algebra
, whereas forcing v1 ⊗ v2 = − v2 ⊗ v1 yields the exterior algebra
.
When a field, F is explicitly stated, a common term used is .
. The minimax theorem of game theory
stating the existence of a unique payoff when all players play optimally can be formulated and proven using vector spaces methods. Representation theory
fruitfully transfers the good understanding of linear algebra and vector spaces to other mathematical domains such as group theory
.
with compact support, in a continuous way: in the above terminology the space of distributions is the (continuous) dual of the test function space. The latter space is endowed with a topology that takes into account not only ƒ itself, but also all its higher derivatives. A standard example is the result of integrating a test function ƒ over some domain Ω: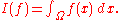
When Ω = {p}, the set consisting of a single point, this reduces to the Dirac distribution, denoted by δ, which associates to a test function ƒ its value at the p: δ(ƒ) = ƒ(p). Distributions are a powerful instrument to solve differential equations. Since all standard analytic notions such as derivatives are linear, they extend naturally to the space of distributions. Therefore the equation in question can be transferred to a distribution space, which is bigger than the underlying function space, so that more flexible methods are available for solving the equation. For example, Green's function
s and fundamental solution
s are usually distributions rather than proper functions, and can then be used to find solutions of the equation with prescribed boundary conditions. The found solution can then in some cases be proven to be actually a true function, and a solution to the original equation (e.g., using the Lax–Milgram theorem, a consequence of the Riesz representation theorem
).
Resolving a periodic function
into a sum of trigonometric function
s forms a Fourier series
, a technique much used in physics and engineering.Although the Fourier series is periodic, the technique can be applied to any L2 function on an interval by considering the function to be continued periodically outside the interval. See The underlying vector space is usually the Hilbert space
L2(0, 2π), for which the functions sin mx and cos mx (m an integer) form an orthogonal basis. The Fourier expansion of an L2 function f is
The coefficients am and bm are called Fourier coefficients of ƒ, and are calculated by the formulas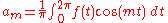
, 
In physical terms the function is represented as a superposition
of sine waves and the coefficients give information about the function's frequency spectrum
. A complex-number form of Fourier series is also commonly used. The concrete formulae above are consequences of a more general mathematical duality
called Pontryagin duality
. Applied to the group
R, it yields the classical Fourier transform; an application in physics are reciprocal lattice
s, where the underlying group is a finite-dimensional real vector space endowed with the additional datum of a lattice encoding positions of atom
s in crystal
s.
Fourier series are used to solve boundary value problem
s in partial differential equations. In 1822, Fourier
first used this technique to solve the heat equation
. A discrete version of the Fourier series can be used in sampling
applications where the function value is known only at a finite number of equally spaced points. In this case the Fourier series is finite and its value is equal to the sampled values at all points. The set of coefficients is known as the discrete Fourier transform
(DFT) of the given sample sequence. The DFT is one of the key tools of digital signal processing
, a field whose applications include radar
, speech encoding
, image compression
. The JPEG
image format is an application of the closely related discrete cosine transform
.
The fast Fourier transform
is an algorithm for rapidly computing the discrete Fourier transform. It is used not only for calculating the Fourier coefficients but, using the convolution theorem
, also for computing the convolution
of two finite sequences. They in turn are applied in digital filter
s and as a rapid multiplication algorithm
for polynomials and large integers (Schönhage-Strassen algorithm
).
, or linearization
, of a surface at a point.That is to say , the plane passing through the point of contact P such that the distance from a point P1 on the surface to the plane is infinitesimally small compared to the distance from P1 to P in the limit as P1 approaches P along the surface. Even in a three-dimensional Euclidean space, there is typically no natural way to prescribe a basis of the tangent plane, and so it is conceived of as an abstract vector space rather than a real coordinate space. The tangent space is the generalization to higher-dimensional differentiable manifold
s.
Riemannian manifold
s are manifolds whose tangent spaces are endowed with a suitable inner product. Derived therefrom, the Riemann curvature tensor
encodes all curvatures of a manifold in one object, which finds applications in general relativity
, for example, where the Einstein curvature tensor describes the matter and energy content of space-time. The tangent space of a Lie group can be given naturally the structure of a Lie algebra and can be used to classify compact Lie groups.
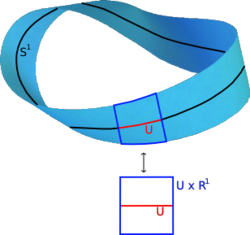A vector bundle is a family of vector spaces parametrized continuously by a topological space
X. More precisely, a vector bundle over X is a topological space E equipped with a continuous map
such that for every x in X, the fiber π−1(x) is a vector space. The case dim V = 1 is called a line bundle
. For any vector space V, the projection X × V → X makes the product X × V into a "trivial" vector bundle. Vector bundles over X are required to be locally a product of X and some (fixed) vector space V: for every x in X, there is a neighborhood U of x such that the restriction of π to π−1(U) is isomorphicThat is, there is a homeomorphism
from π−1(U) to V × U which restricts to linear isomorphisms between fibers. to the trivial bundle U × V → U. Despite their locally trivial character, vector bundles may (depending on the shape of the underlying space X) be "twisted" in the large, i.e., the bundle need not be (globally isomorphic to) the trivial bundle For example, the Möbius strip
can be seen as a line bundle over the circle S1 (by identifying open intervals with the real line). It is, however, different from the cylinder
S1 × R, because the latter is orientable whereas the former is not.
Properties of certain vector bundles provide information about the underlying topological space. For example, the tangent bundle
consists of the collection of tangent space
s parametrized by the points of a differentiable manifold. The tangent bundle of the circle S1 is globally isomorphic to S1 × R, since there is a global nonzero vector field
on S1.A line bundle, such as the tangent bundle of S1 is trivial if and only if there is a section
that vanishes nowhere, see . The sections of the tangent bundle are just vector field
s. In contrast, by the hairy ball theorem
, there is no (tangent) vector field on the 2-sphere S2 which is everywhere nonzero. K-theory
studies the isomorphism classes of all vector bundles over some topological space. In addition to deepening topological and geometrical insight, it has purely algebraic consequences, such as the classification of finite-dimensional real division algebra
s: R, C, the quaternion
s H and the octonion
s.
The cotangent bundle
of a differentiable manifold consists, at every point of the manifold, of the dual of the tangent space, the cotangent space
. Sections
of that bundle are known as differential one-form
s.
what vector spaces are to fields. The very same axioms, applied to a ring R instead of a field F yield modules. The theory of modules, compared to vector spaces, is complicated by the presence of ring elements that do not have multiplicative inverse
s. For example, modules need not have bases, as the Z-module (i.e., abelian group
) Z/2Z
shows; those modules that do (including all vector spaces) are known as free module
s.
To see why the requirement that for every scalar there exist multiplicative inverse makes a difference, consider this: the fact that every vector space has a basis amounts to saying that every vector space is a free module. The proof of this fact fails for general modules over any ring(at least for modules of finite type) in the step "in every list b of linearly dependent vectors, it is possible to remove one vector from b without changing span of b". This does not hold in a general module, but holds in any vector space. So when we have a linearly dependent finite list of vectors that spans the whole vector space at hand (which must exist in a finite-dimensional vector space), we can remove one vector from the list and the list will still span the whole vector space. We can repeat this process until we get a basis; we cannot do this in general in a module. As it turns out, requiring that a module be over a field instead of a ring is a sufficient condition for this to hold.
Nevertheless, a vector space can be compactly defined as a module
over a ring
which is a field
with the elements being called vectors. The algebro-geometric interpretation of commutative rings via their spectrum
allows the development of concepts such as locally free modules, the algebraic counterpart to vector bundles.
. In particular, a vector space is an affine space over itself, by the map
If W is a vector space, then an affine subspace is a subset of W obtained by translating a linear subspace V by a fixed vector ; this space is denoted by x + V (it is a coset
of V in W) and consists of all vectors of the form for An important example is the space of solutions of a system of inhomogeneous linear equations
generalizing the homogeneous case b = 0 above. The space of solutions is the affine subspace x + V where x is a particular solution of the equation, and V is the space of solutions of the homogeneous equation (the nullspace of A).
The set of one-dimensional subspaces of a fixed finite-dimensional vector space V is known as projective space; it may be used to formalize the idea of parallel
lines intersecting at infinity. Grassmannians and flag manifold
s generalize this by parametrizing linear subspaces of fixed dimension k and flags of subspaces, respectively.
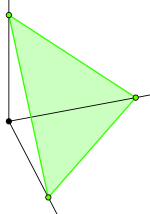Over an ordered field
, notably the real numbers, there are the added notions of convex analysis
, most basically a cone
, which allows only non-negative linear combinations, and a convex set
, which allows only non-negative linear combinations that sum to 1. A convex set can be seen as the combinations of the axioms for an affine space and a cone, which is reflected in the standard space for it, the n-simplex
, being the intersection of the affine hyperplane and orthant
. Such spaces are particularly used in linear programming
.
In the language of universal algebra
, a vector space is an algebra over the universal vector space K∞ of finite sequences of coefficients, corresponding to finite sums of vectors, while an affine space is an algebra over the universal affine hyperplane in here (of finite sequences summing to 1), a cone is an algebra over the universal orthant, and a convex set is an algebra over the universal simplex. This geometrizes the axioms in terms of "sums with (possible) restrictions on the coordinates".
Many concepts in linear algebra have analogs in convex analysis, including basic ones such as basis and span (such as in the form of convex hull
), and notably including duality (in the form of dual polyhedron
, dual cone, dual problem
). Unlike linear algebra, however, where every vector space or affine space is isomorphic to the standard spaces, not every convex set or cone is isomorphic to the simplex or orthant. Rather, there is always a map from the simplex onto a polytope, given by generalized barycentric coordinates, and a dual map from a polytope into the orthant (of dimension equal to the number of faces) given by slack variable
s, but these are rarely isomorphisms – most polytopes are not a simplex or an orthant.
Mathematical structure
In mathematics, a structure on a set, or more generally a type, consists of additional mathematical objects that in some manner attach to the set, making it easier to visualize or work with, or endowing the collection with meaning or significance....
formed by a collection of vectors
Vector (mathematics and physics)
In mathematics and physics, a vector is an element of a vector space. If n is a non negative integer and K is either the field of the real numbers or the field of the complex number, then K^n is naturally endowed with a structure of vector space, where K^n is the set of the ordered sequences of n...
: objects that may be added together and multiplied
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
("scaled") by numbers, called scalars
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
in this context. Scalars are often taken to be real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, but one may also consider vector spaces with scalar multiplication by complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, or even more general fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
instead. The operations of vector addition and scalar multiplication have to satisfy certain requirements, called axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s, listed below. An example of a vector space is that of Euclidean vectors which are often used to represent physical
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
quantities such as force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
s: any two forces (of the same type) can be added to yield a third, and the multiplication of a force vector by a real factor is another force vector. In the same vein, but in more geometric
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
parlance, vectors representing displacements in the plane or in three-dimensional space
Three-dimensional space
Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...
also form vector spaces.
Vector spaces are the subject of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
and are well understood from this point of view, since vector spaces are characterized by their dimension, which, roughly speaking, specifies the number of independent directions in the space. The theory is further enhanced by introducing on a vector space some additional structure, such as a norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
or inner product. Such spaces arise naturally in mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, mainly in the guise of infinite-dimensional function spaces whose vectors are functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
. Analytical problems call for the ability to decide if a sequence of vectors converges
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
to a given vector. This is accomplished by considering vector spaces with additional data, mostly spaces endowed with a suitable topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, thus allowing the consideration of proximity and continuity
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
issues. These topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s, in particular Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s and Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s, have a richer theory.
Historically, the first ideas leading to vector spaces can be traced back as far as 17th century's analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
, matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, systems of linear equation
Linear equation
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
s, and Euclidean vectors. The modern, more abstract treatment, first formulated by Giuseppe Peano
Giuseppe Peano
Giuseppe Peano was an Italian mathematician, whose work was of philosophical value. The author of over 200 books and papers, he was a founder of mathematical logic and set theory, to which he contributed much notation. The standard axiomatization of the natural numbers is named the Peano axioms in...
in the late 19th century, encompasses more general objects than Euclidean space, but much of the theory can be seen as an extension of classical geometric ideas like line
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
s, planes and their higher-dimensional analogs.
Today, vector spaces are applied throughout mathematics, science
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
. They are the appropriate linear-algebraic notion to deal with systems of linear equations; offer a framework for Fourier expansion
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
, which is employed in image compression
Image compression
The objective of image compression is to reduce irrelevance and redundancy of the image data in order to be able to store or transmit data in an efficient form.- Lossy and lossless compression :...
routines; or provide an environment that can be used for solution techniques for partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s. Furthermore, vector spaces furnish an abstract, coordinate-free way of dealing with geometrical and physical objects such as tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
s. This in turn allows the examination of local properties of manifolds by linearization techniques. Vector spaces may be generalized in several directions, leading to more advanced notions in geometry and abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
.
First example: arrows in the plane
The concept of vector space will first be explained by describing two particular examples. The first example of a vector space consists of arrowArrow
An arrow is a shafted projectile that is shot with a bow. It predates recorded history and is common to most cultures.An arrow usually consists of a shaft with an arrowhead attached to the front end, with fletchings and a nock at the other.- History:...
s in a fixed plane, starting at one fixed point. This is used in physics to describe force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
s or velocities
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
. Given any two such arrows, v and w, the parallelogram
Parallelogram
In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
spanned by these two arrows contains one diagonal arrow that starts at the origin, too. This new arrow is called the sum of the two arrows and is denoted . Another operation that can be done with arrows is scaling: given any positive real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
a, the arrow that has the same direction as v, but is dilated or shrunk by multiplying its length by a, is called multiplication of v by a. It is denoted . When a is negative, is defined as the arrow pointing in the opposite direction, instead.
The following shows a few examples: if a = 2, the resulting vector has the same direction as w, but is stretched to the double length of w (right image below). Equivalently 2 · w is the sum . Moreover, (−1) · v = −v has the opposite direction and the same length as v (blue vector pointing down in the right image).
Second example: ordered pairs of numbers
A second key example of a vector space is provided by pairs of real numbers x and y. (The order of the components x and y is significant, so such a pair is also called an ordered pairOrdered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
.) Such a pair is written as (x, y). The sum of two such pairs and multiplication of a pair with a number is defined as follows: + (x2, y2) = (x1 + x2, y1 + y2)
and
- a · (x, y) = (ax, ay).
Definition
A vector space over a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F is a set V together with two binary operators
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
that satisfy the eight axioms listed below. Elements of V are called vectors. Elements of F are called scalars. In this article, vectors are differentiated from scalars by boldface.It is also common, especially in physics, to denote vectors with an arrow on top:
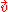. In the two examples above, our set consists of the planar arrows with fixed starting point and of pairs of real numbers, respectively, while our field is the real numbers. The first operation, vector addition, takes any two vectors v and w and assigns to them a third vector which is commonly written as and called the sum of these two vectors. The second operation takes any scalar a and any vector v and gives another . In view of the first example, where the multiplication is done by rescaling the vector v by a scalar a, the multiplication is called scalar multiplicationScalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
of v by a.
To qualify as a vector space, the set V and the operations of addition and multiplication have to adhere to a number of requirements called axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s. In the list below, let u, v, w be arbitrary vectors in V, and a, b be scalars in F.
| Axiom | Signification |
| Associativity Associativity In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not... of addition |
v1 + (v2 + v3) = (v1 + v2) + v3. |
| Commutativity Commutativity In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it... of addition |
v1 + v2 = v2 + v1. |
| Identity element Identity element In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them... of addition |
There exists an element 0 ∈ V, called the zero vector, such that v + 0 = v for all v ∈ V. |
| Inverse element Inverse element In abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element... s of addition |
For all v ∈ V, there exists an element -v ∈ V, called the additive inverse Additive inverse In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a.... of v, such that v + (-v) = 0. |
| Distributivity Distributivity In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:... of scalar multiplication with respect to vector addition |
s(v1 + v2) = sv1 + sv2. |
| Distributivity of scalar multiplication with respect to field addition | (n1 + n2)v = n1v + n2v. |
| Respect of scalar multiplication over field's multiplication | n1 (n2 s) = (n1 n2)s This axiom is not asserting the associativity of an operation, since there are two operations in question, scalar multiplication: n2s; and field multiplication: n1 n2. |
| Identity element of scalar multiplication | 1s = s, where 1 denotes the multiplicative identity in F. |
These axioms generalize properties of the vectors introduced in the above examples. Indeed, the result of addition of two ordered pairs (as in the second example above) does not depend on the order of the summands: + (xw, yw) = (xw, yw) + (xv, yv),
Likewise, in the geometric example of vectors as arrows, v + w = w + v, since the parallelogram defining the sum of the vectors is independent of the order of the vectors. All other axioms can be checked in a similar manner in both examples. Thus, by disregarding the concrete nature of the particular type of vectors, the definition incorporates these two and many more examples in one notion of vector space.
Subtraction of two vectors and division by a (non-zero) scalar can be performed via
- v − w = v + (−w),
- v / a = (1 / a) · v.
The concept introduced above is called a real vector space. The word "real" refers to the fact that vectors can be multiplied by real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, as opposed to, say, complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. When scalar multiplication is defined for complex numbers, the denomination complex vector space is used. These two cases are the ones used most often in engineering. The most general definition of a vector space allows scalars to be elements of a fixed field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F. Then, the notion is known as F-vector spaces or vector spaces over F. A field is, essentially, a set of numbers possessing addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
, multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
and division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
operations.Some authors (such as ) restrict attention to the fields R or C, but most of the theory is unchanged over an arbitrary field. For example, rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s also form a field.
In contrast to the intuition stemming from vectors in the plane and higher-dimensional cases, there is, in general vector spaces, no notion of nearness, angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s or distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
s. To deal with such matters, particular types of vector spaces are introduced; see below.
Alternative formulations and elementary consequences
The requirement that vector addition and scalar multiplication be binary operations includes (by definition of binary operations) a property called closureClosure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
: that u + v and av are in V for all a in F, and u, v in V. Some older sources mention these properties as separate axioms.
In the parlance of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the first four axioms can be subsumed by requiring the set of vectors to be an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
under addition. The remaining axioms give this group an F-module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
structure. In other words there is a ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
ƒ from the field F into the endomorphism ring
Endomorphism ring
In abstract algebra, one associates to certain objects a ring, the object's endomorphism ring, which encodes several internal properties of the object; this may be denoted End...
of the group of vectors. Then scalar multiplication av is defined as (ƒ(a))(v).
There are a number of direct consequences of the vector space axioms. Some of them derive from elementary group theory, applied to the additive group of vectors: for example the zero vector 0 of V and the additive inverse −v of any vector v are unique. Other properties follow from the distributive law, for example av equals 0 if and only if a equals 0 or v equals 0.
History
Vector spaces stem from affine geometryAffine geometry
In mathematics affine geometry is the study of geometric properties which remain unchanged by affine transformations, i.e. non-singular linear transformations and translations...
, via the introduction of coordinates in the plane or three-dimensional space. Around 1636, Descartes
René Descartes
René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
and Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
founded analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
by equating solutions to an equation of two variables with points on a plane curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
. To achieve geometric solutions without using coordinates, Bolzano introduced, in 1804, certain operations on points, lines and planes, which are predecessors of vectors. This work was made use of in the conception of barycentric coordinates
Barycentric coordinates (mathematics)
In geometry, the barycentric coordinate system is a coordinate system in which the location of a point is specified as the center of mass, or barycenter, of masses placed at the vertices of a simplex . Barycentric coordinates are a form of homogeneous coordinates...
by Möbius
August Ferdinand Möbius
August Ferdinand Möbius was a German mathematician and theoretical astronomer.He is best known for his discovery of the Möbius strip, a non-orientable two-dimensional surface with only one side when embedded in three-dimensional Euclidean space. It was independently discovered by Johann Benedict...
in 1827. The foundation of the definition of vectors was Bellavitis
Giusto Bellavitis
Giusto Bellavitis was an Italian mathematician. He is known for his contributions to algebraic geometry.-Awards:* Fellow of the Istituto Veneto in 1840* Fellow of the Società Italiana dei Quaranta in 1850...
' notion of the bipoint, an oriented segment one of whose ends is the origin and the other one a target. Vectors were reconsidered with the presentation of complex numbers by Argand
Jean-Robert Argand
Jean-Robert Argand was a gifted amateur mathematician. In 1806, while managing a bookstore in Paris, he published the idea of geometrical interpretation of complex numbers known as the Argand diagram.-Life:...
and Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
and the inception of quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s and biquaternions by the latter. They are elements in R2, R4, and R8; treating them using linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
s goes back to Laguerre in 1867, who also defined systems of linear equations.
In 1857, Cayley
Arthur Cayley
Arthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....
introduced the matrix notation which allows for a harmonization and simplification of linear maps. Around the same time, Grassmann studied the barycentric calculus initiated by Möbius. He envisaged sets of abstract objects endowed with operations. In his work, the concepts of linear independence
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
and dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
, as well as scalar products are present. Actually Grassmann's 1844 work exceeds the framework of vector spaces, since his considering multiplication, too, led him to what are today called algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
s. Peano was the first to give the modern definition of vector spaces and linear maps in 1888.
An important development of vector spaces is due to the construction of function spaces by Lebesgue
Henri Lebesgue
Henri Léon Lebesgue was a French mathematician most famous for his theory of integration, which was a generalization of the seventeenth century concept of integration—summing the area between an axis and the curve of a function defined for that axis...
. This was later formalized by Banach
Stefan Banach
Stefan Banach was a Polish mathematician who worked in interwar Poland and in Soviet Ukraine. He is generally considered to have been one of the 20th century's most important and influential mathematicians....
and Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
, around 1920. At that time, algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
and the new field of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
began to interact, notably with key concepts such as spaces of p-integrable functions
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
and Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s. Vector spaces, including infinite-dimensional ones, then became a firmly established notion, and many mathematical branches started making use of this concept.
Coordinate and function spaces
The first example of a vector space over a field F is the field itself, equipped with its standard addition and multiplication. This is the case n = 1 of a vector space usually denoted Fn, known as the coordinate spaceCoordinate space
In mathematics, specifically in linear algebra, the coordinate space, Fn, is the prototypical example of an n-dimensional vector space over a field F. It can be defined as the product space of F over a finite index set.-Definition:...
whose elements are n-tuples
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
(sequences of length n):, where the ai are elements of F.
The case F = R and n = 2 was discussed in the introduction above. Infinite coordinate sequences, and more generally functions from any fixed set Ω to a field F also form vector spaces, by performing addition and scalar multiplication pointwise. That is, the sum of two functions ƒ and g is given by(w) = ƒ(w) + g(w)
and similarly for multiplication. Such function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
s occur in many geometric situations, when Ω is the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
or an interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
, or other subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of Rn. Many notions in topology and analysis, such as continuity
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, integrability
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
or differentiability are well-behaved with respect to linearity: sums and scalar multiples of functions possessing such a property still have that property. Therefore, the set of such functions are vector spaces. They are studied in greater detail using the methods of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, see below. Algebraic constraints also yield vector spaces: the vector space F[x
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
] is given by polynomial functions:
- ƒ(x) = r0 + r1x + ... + rn−1xn−1 + rnxn, where the coefficientCoefficientIn mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s r0, ..., rn are in F.
Linear equations
Systems of homogeneous linear equations are closely tied to vector spaces. For example, the solutions of| a | + | 3b | + | c | = 0 |
| 4a | + | 2b | + | 2c | = 0 |
are given by triples with arbitrary a, b = a/2, and c = −5a/2. They form a vector space: sums and scalar multiples of such triples still satisfy the same ratios of the three variables; thus they are solutions, too. Matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
can be used to condense multiple linear equations as above into one vector equation, namely
- Ax = 0,
where A =
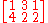is the matrix containing the coefficients of the given equations, x is the vector Ax denotes the matrix product and 0 = (0, 0) is the zero vector. In a similar vein, the solutions of homogeneous linear differential equations form vector spaces. For example
- ƒ
(x) + 2ƒ ' (x) + ƒ(x) = 0
yields ƒ(x) = a e−x + bx e−x, where a and b are arbitrary constants, and ex is the natural exponential function.
Field extensions
Field extensionField extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
s F / E ("F over E") provide another class of examples of vector spaces, particularly in algebra and algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
: a field F containing a smaller field E becomes an E-vector space, by the given multiplication and addition operations of F. For example the complex numbers are a vector space over R. A particularly interesting type of field extension in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
is Q(α), the extension of the rational numbers Q by a fixed complex number α. Q(α) is the smallest field containing the rationals and a fixed complex number α. Its dimension as a vector space over Q depends on the choice of α.
Bases and dimension
Bases reveal the structure of vector spaces in a concise way. A basis is defined as a (finite or infinite) set B = {vi}i ∈ I of vectors vi indexed by some index setIndex set
In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
I that spans the whole space, and is minimal with this property. The former means that any vector v can be expressed as a finite sum (called linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
) of the basis elements
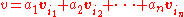,where the ak are scalars and vik (k = 1, ..., n) elements of the basis B. Minimality, on the other hand, is made formal by requiring B to be linearly independent. A set of vectors is said to be linearly independent if none of its elements can be expressed as a linear combination of the remaining ones. Equivalently, an equation
can only hold if all scalars a1, ..., an equal zero. Linear independence ensures that the representation of any vector in terms of basis vectors, the existence of which is guaranteed by the requirement that the basis span V, is unique. This is referred to as the coordinatized viewpoint of vector spaces, by viewing basis vectors as generalizations of coordinate vectors x, y, z in R3 and similarly in higher-dimensional cases.
The coordinate vector
Coordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
s e1 = (1, 0, ..., 0), e2 = (0, 1, 0, ..., 0), to en = (0, 0, ..., 0, 1), form a basis of Fn, called the standard basis
Standard basis
In mathematics, the standard basis for a Euclidean space consists of one unit vector pointing in the direction of each axis of the Cartesian coordinate system...
, since any vector (x1, x2, ..., xn) can be uniquely expressed as a linear combination of these vectors: = x1(1, 0, ..., 0) + x2(0, 1, 0, ..., 0) + ... + xn(0, ..., 0, 1) = x1e1 + x2e2 + ... + xnen.
Every vector space has a basis. This follows from Zorn's lemma
Zorn's lemma
Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
, an equivalent formulation of the axiom of choice. Given the other axioms of Zermelo-Fraenkel set theory, the existence of bases is equivalent to the axiom of choice. The ultrafilter lemma, which is weaker than the axiom of choice, implies that all bases of a given vector space have the same number of elements, or cardinality. It is called the dimension of the vector space, denoted dim V. If the space is spanned by finitely many vectors, the above statements can be proven without such fundamental input from set theory.
The dimension of the coordinate space Fn is n, by the basis exhibited above. The dimension of the polynomial ring F[x] introduced above is countably infinite, a basis is given by 1, x, x2, ... A fortiori, the dimension of more general function spaces, such as the space of functions on some (bounded or unbounded) interval, is infinite.The indicator functions of intervals (of which there are infinitely many) are linearly independent, for example. Under suitable regularity assumptions on the coefficients involved, the dimension of the solution space of a homogeneous ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
equals the degree of the equation. For example, the solution space for the above equation is generated by e−x and xe−x. These two functions are linearly independent over R, so the dimension of this space is two, as is the degree of the equation.
The dimension (or degree) of the field extension Q(α) over Q depends on α. If α satisfies some polynomial equation
("α is algebraic
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
"), the dimension is finite. More precisely, it equals the degree of the minimal polynomial
Minimal polynomial (field theory)
In field theory, given a field extension E / F and an element α of E that is an algebraic element over F, the minimal polynomial of α is the monic polynomial p, with coefficients in F, of least degree such that p = 0...
having α as a root. For example, the complex numbers C are a two-dimensional real vector space, generated by 1 and the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
i. The latter satisfies i2 + 1 = 0, an equation of degree two. Thus, C is a two-dimensional R-vector space (and, as any field, one-dimensional as a vector space over itself, C). If α is not algebraic, the dimension of Q(α) over Q is infinite. For instance, for α = π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
there is no such equation, in other words π is transcendental
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
.
Linear maps and matrices
The relation of two vector spaces can be expressed by linear map or linear transformation. They are functionsFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that reflect the vector space structure—i.e., they preserve sums and scalar multiplication:
An isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
is a linear map such that there exists an inverse map , which is a map such that the two possible compositions
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
and are identity maps
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
. Equivalently, ƒ is both one-to-one (injective) and onto (surjective). If there exists an isomorphism between V and W, the two spaces are said to be isomorphic; they are then essentially identical as vector spaces, since all identities holding in V are, via ƒ, transported to similar ones in W, and vice versa via g.
For example, the vector spaces in the introduction are isomorphic: a planar arrow v departing at the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
of some (fixed) coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
can be expressed as an ordered pair by considering the x- and y-component of the arrow, as shown in the image at the right. Conversely, given a pair (x, y), the arrow going by x to the right (or to the left, if x is negative), and y up (down, if y is negative) turns back the arrow v.
Linear maps V → W between two fixed vector spaces form a vector space HomF(V, W), also denoted L(V, W). The space of linear maps from V to F is called the dual vector space, denoted V∗. Via the injective natural map V → V∗∗, any vector space can be embedded into its bidual; the map is an isomorphism if and only if the space is finite-dimensional.
Once a basis of V is chosen, linear maps are completely determined by specifying the images of the basis vectors, because any element of V is expressed uniquely as a linear combination of them. If dim V = dim W, a 1-to-1 correspondence
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between fixed bases of V and W gives rise to a linear map that maps any basis element of V to the corresponding basis element of W. It is an isomorphism, by its very definition. Therefore, two vector spaces are isomorphic if their dimensions agree and vice versa. Another way to express this is that any vector space is completely classified (up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
isomorphism) by its dimension, a single number. In particular, any n-dimensional F-vector space V is isomorphic to Fn. There is, however, no "canonical" or preferred isomorphism; actually an isomorphism is equivalent to the choice of a basis of V, by mapping the standard basis of Fn to V, via φ. Appending an automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
, i.e. an isomorphism yields another isomorphism , the composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
of ψ and φ, and therefore a different basis of V. The freedom of choosing a convenient basis is particularly useful in the infinite-dimensional context, see below.
Matrices
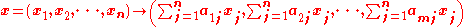, where denotes summationSummation
Summation is the operation of adding a sequence of numbers; the result is their sum or total. If numbers are added sequentially from left to right, any intermediate result is a partial sum, prefix sum, or running total of the summation. The numbers to be summed may be integers, rational numbers,...
,
or, using the matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
of the matrix A with the coordinate vector x:
- x ↦
Moreover, after choosing bases of V and W, any linear map is uniquely represented by a matrix via this assignment.
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
det (A) of a square matrix A is a scalar that tells whether the associated map is an isomorphism or not: to be so it is sufficient and necessary that the determinant is nonzero. The linear transformation of Rn corresponding to a real n-by-n matrix is orientation preserving
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
if and only if the determinant is positive.
Eigenvalues and eigenvectors
EndomorphismEndomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
s, linear maps , are particularly important since in this case vectors v can be compared with their image under ƒ, ƒ(v). Any nonzero vector v satisfying λv = ƒ(v), where λ is a scalar, is called an eigenvector of ƒ with eigenvalue λ.The nomenclature derives from German
German language
German is a West Germanic language, related to and classified alongside English and Dutch. With an estimated 90 – 98 million native speakers, German is one of the world's major languages and is the most widely-spoken first language in the European Union....
"eigen", which means own or proper. Equivalently, v is an element of the kernel of the difference (where Id is the identity map
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
If V is finite-dimensional, this can be rephrased using determinants: ƒ having eigenvalue λ is equivalent to
- det (
By spelling out the definition of the determinant, the expression on the left hand side can be seen to be a polynomial function in λ, called the characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of ƒ. If the field F is large enough to contain a zero of this polynomial (which automatically happens for F algebraically closed
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
, such as F = C) any linear map has at least one eigenvector. The vector space V may or may not possess an eigenbasis, a basis consisting of eigenvectors. This phenomenon is governed by the Jordan canonical form of the map.. See also Jordan–Chevalley decomposition. The set of all eigenvectors corresponding to a particular eigenvalue of ƒ forms a vector space known as the eigenspace corresponding to the eigenvalue (and ƒ) in question. To achieve the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
, the corresponding statement in the infinite-dimensional case, the machinery of functional analysis is needed, see below.
Basic constructions
In addition to the above concrete examples, there are a number of standard linear algebraic constructions that yield vector spaces related to given ones. In addition to the definitions given below, they are also characterized by universal propertiesUniversal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
, which determine an object X by specifying the linear maps from X to any other vector space.
Subspaces and quotient spaces
A nonempty subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
W of a vector space V that is closed under addition and scalar multiplication (and therefore contains the 0-vector of V) is called a subspace of V. Subspaces of V are vector spaces (over the same field) in their own right. The intersection of all subspaces containing a given set S of vectors is called its span
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
, and is the smallest subspace of V containing the set S. Expressed in terms of elements, the span is the subspace consisting of all the linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
s of elements of S.
The counterpart to subspaces are quotient vector spaces. Given any subspace W ⊂ V, the quotient space V/W ("V modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
W") is defined as follows: as a set, it consists of v + W = {v + w, w ∈ W}, where v is an arbitrary vector in V. The sum of two such elements v1 + W and v2 + W is and scalar multiplication is given by a · (v + W) = (a · v) + W. The key point in this definition is that v1 + W = v2 + W if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the difference of v1 and v2 lies in W.Some authors (such as ) choose to start with this equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
and derive the concrete shape of V/W from this. This way, the quotient space "forgets" information that is contained in the subspace W.
The kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
ker(ƒ) of a linear map ƒ: V → W consists of vectors v that are mapped to 0 in W. Both kernel and image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
im(ƒ) = {ƒ(v), v ∈ V} are subspaces of V and W, respectively. The existence of kernels and images is part of the statement that the category of vector spaces
Category of vector spaces
In mathematics, especially category theory, the category K-Vect has all vector spaces over a fixed field K as objects and K-linear transformations as morphisms...
(over a fixed field F) is an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
, i.e. a corpus of mathematical objects and structure-preserving maps between them (a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
) that behaves much like the category of abelian groups
Category of abelian groups
In mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category....
. Because of this, many statements such as the first isomorphism theorem (also called rank-nullity theorem
Rank-nullity theorem
In mathematics, the rank–nullity theorem of linear algebra, in its simplest form, states that the rank and the nullity of a matrix add up to the number of columns of the matrix. Specifically, if A is an m-by-n matrix over some field, thenThis applies to linear maps as well...
in matrix-related terms)
and the second and third isomorphism theorem can be formulated and proven in a way very similar to the corresponding statements for groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
.
An important example is the kernel of a linear map x ↦ Ax for some fixed matrix A, as above. The kernel of this map is the subspace of vectors x such that Ax = 0, which is precisely the set of solutions to the system of homogeneous linear equations belonging to A. This concept also extends to linear differential equations
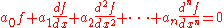, where the coefficients ai are functions in x, too.In the corresponding map
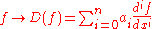,the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s of the function ƒ appear linearly (as opposed to ƒ
Direct product and direct sum
The direct product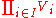 of a family of vector spaces Vi consists of the set of all tuples (vi)i ∈ I, which specify for each index i in some index setIndex set
In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
I an element vi of Vi. Addition and scalar multiplication is performed componentwise. A variant of this construction is the direct sum
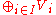(also called coproductCoproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
and denoted
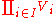), where only tuples with finitely many nonzero vectors are allowed. If the index set I is finite, the two constructions agree, but differ otherwise.Tensor product
The tensor product V ⊗F W, or simply V ⊗ W, of two vector spaces V and W is one of the central notions of multilinear algebraMultilinear algebra
In mathematics, multilinear algebra extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of p-vectors and multivectors with Grassmann algebra.-Origin:In a vector space...
which deals with extending notions such as linear maps to several variables. A map is called bilinear if g is linear in both variables v and w. That is to say, for fixed w the map is linear in the sense above and likewise for fixed v.
The tensor product is a particular vector space that is a universal recipient of bilinear maps g, as follows. It is defined as the vector space consisting of finite (formal) sums of symbols called tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
s
- v1 ⊗ w1 + v2 ⊗ w2 + ... + vn ⊗ wn,
subject to the rules
- a · (v ⊗ w) = (a · v) ⊗ w = v ⊗ (a · w), where a is a scalar, ⊗ w = v1 ⊗ w + v2 ⊗ w, and
- v ⊗ (w1 + w2) = v ⊗ w1 + v ⊗ w2.
These rules ensure that the map ƒ from the V × W to V ⊗ W that maps a tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
(v, w) to is bilinear. The universality states that given any vector space X and any bilinear map there exists a unique map u, shown in the diagram with a dotted arrow, whose composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
with ƒ equals g: u(v ⊗ w) = g(v, w). This is called the universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
of the tensor product, an instance of the method—much used in advanced abstract algebra—to indirectly define objects by specifying maps from or to this object.
Vector spaces with additional structure
From the point of view of linear algebra, vector spaces are completely understood insofar as any vector space is characterized, up to isomorphism, by its dimension. However, vector spaces ad hoc do not offer a framework to deal with the question—crucial to analysis—whether a sequence of functions convergesLimit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
to another function. Likewise, linear algebra is not adapted to deal with infinite series, since the addition operation allows only finitely many terms to be added. Therefore, the needs of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
require considering additional structures. Much the same way the axiomatic treatment of vector spaces reveals their essential algebraic features, studying vector spaces with additional data abstractly turns out to be advantageous, too.
A first example of an additional datum is an order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
≤, a token by which vectors can be compared. For example, n-dimensional real space Rn can be ordered by comparing its vectors componentwise. Ordered vector space
Ordered vector space
In mathematics an ordered vector space or partially ordered vector space is a vector space equipped with a partial order which is compatible with the vector space operations.- Definition:...
s, for example Riesz space
Riesz space
In mathematics a Riesz space, lattice-ordered vector space or vector lattice is an ordered vector space where the order structure is a lattice....
s, are fundamental to Lebesgue integration
Lebesgue integration
In mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
, which relies on the ability to express a function as a difference of two positive functions
- ƒ = ƒ+ − ƒ−,
where ƒ+ denotes the positive part of ƒ and ƒ− the negative part.
Normed vector spaces and inner product spaces
"Measuring" vectors is done by specifying a normNorm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
, a datum which measures lengths of vectors, or by an inner product, which measures angles between vectors. Norms and inner products are denoted
and , respectively. The datum of an inner product entails that lengths of vectors can be defined too, by defining the associated norm 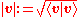. Vector spaces endowed with such data are known as normed vector spaces and inner product spaces, respectively.Coordinate space Fn can be equipped with the standard dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
:
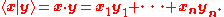
In R2, this reflects the common notion of the angle between two vectors x and y, by the law of cosines
Law of cosines
In trigonometry, the law of cosines relates the lengths of the sides of a plane triangle to the cosine of one of its angles. Using notation as in Fig...
:
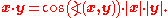
Because of this, two vectors satisfying
are called orthogonal. An important variant of the standard dot product is used in Minkowski spaceMinkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
: R4 endowed with the Lorentz product
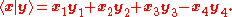
In contrast to the standard dot product, it is not positive definite:
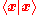also takes negative values, for example for x = (0, 0, 0, 1). Singling out the fourth coordinate—corresponding to time, as opposed to three space-dimensions—makes it useful for the mathematical treatment of special relativitySpecial relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
.
Topological vector spaces
Convergence questions are treated by considering vector spaces V carrying a compatible topologyTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, a structure that allows one to talk about elements being close to each other. Compatible here means that addition and scalar multiplication have to be continuous maps. Roughly, if x and y in V, and a in F vary by a bounded amount, then so do x + y and ax.This requirement implies that the topology gives rise to a uniform structure, To make sense of specifying the amount a scalar changes, the field F also has to carry a topology in this context; a common choice are the reals or the complex numbers.
In such topological vector spaces one can consider series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
of vectors. The infinite sum
denotes the limit
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
of the corresponding finite partial sums of the sequence (ƒi)i∈N of elements of V. For example, the ƒi could be (real or complex) functions belonging to some function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
V, in which case the series is a function series
Function series
In calculus, a function series is a series, where the summands are not just real or complex numbers but functions.Examples of function series include power series, Laurent series, Fourier series, etc....
. The mode of convergence
Modes of convergence
In mathematics, there are many senses in which a sequence or a series is said to be convergent. This article describes various modes of convergence in the settings where they are defined...
of the series depends on the topology imposed on the function space. In such cases, pointwise convergence
Pointwise convergence
In mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
and uniform convergence are two prominent examples.
A way to ensure the existence of limits of certain infinite series is to restrict attention to spaces where any Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
has a limit; such a vector space is called complete. Roughly, a vector space is complete provided that it contains all necessary limits. For example, the vector space of polynomials on the unit interval [0,1], equipped with the topology of uniform convergence is not complete because any continuous function on [0,1] can be uniformly approximated by a sequence of polynomials, by the Weierstrass approximation theorem. In contrast, the space of all continuous functions on [0,1] with the same topology is complete. A norm gives rise to a topology by defining that a sequence of vectors vn converges to v if and only if
Banach and Hilbert spaces are complete topological spaces whose topologies are given, respectively, by a norm and an inner product. Their study—a key piece of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
—focusses on infinite-dimensional vector spaces, since all norms on finite-dimensional topological vector spaces give rise to the same notion of convergence. The image at the right shows the equivalence of the 1-norm and ∞-norm on R2: as the unit "balls" enclose each other, a sequence converges to zero in one norm if and only if it so does in the other norm. In the infinite-dimensional case, however, there will generally be inequivalent topologies, which makes the study of topological vector spaces richer than that of vector spaces without additional data.
From a conceptual point of view, all notions related to topological vector spaces should match the topology. For example, instead of considering all linear maps (also called functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
s) V → W, maps between topological vector spaces are required to be continuous. In particular, the (topological) dual space V∗ consists of continuous functionals V → R (or C). The fundamental Hahn–Banach theorem
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
is concerned with separating subspaces of appropriate topological vector spaces by continuous functionals.
Banach spaces
Banach spaces, introduced by Stefan BanachStefan Banach
Stefan Banach was a Polish mathematician who worked in interwar Poland and in Soviet Ukraine. He is generally considered to have been one of the 20th century's most important and influential mathematicians....
, are complete normed vector spaces. A first example is the vector space ℓ p
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
consisting of infinite vectors with real entries x = (x1, x2, ...) whose p-norm given by
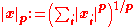for p < ∞ and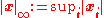 is finite. The topologies on the infinite-dimensional space ℓ p are inequivalent for different p. E.g. the sequence of vectors xn = (2−n, 2−n, ..., 2−n, 0, 0, ...), i.e. the first 2n components are 2−n, the following ones are 0, converges to the zero vector for p = ∞, but does not for p = 1:
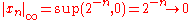, but 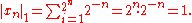More generally than sequences of real numbers, functions ƒ: Ω → R are endowed with a norm that replaces the above sum by the Lebesgue integral
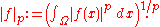
The space of integrable functions on a given domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
Ω (for example an interval) satisfying |ƒ|p < ∞, and equipped with this norm are called Lebesgue spaces
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
, denoted Lp(Ω).The triangle inequality for |−|p is provided by the Minkowski inequality
Minkowski inequality
In mathematical analysis, the Minkowski inequality establishes that the Lp spaces are normed vector spaces. Let S be a measure space, let 1 ≤ p ≤ ∞ and let f and g be elements of Lp...
. For technical reasons, in the context of functions one has to identify functions that agree almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
to get a norm, and not only a seminorm. These spaces are complete. (If one uses the Riemann integral
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
instead, the space is not complete, which may be seen as a justification for Lebesgue's integration theory."Many functions in L2 of Lebesgue measure, being unbounded, cannot be integrated with the classical Riemann integral. So spaces of Riemann integrable functions would not be complete in the L2 norm, and the orthogonal decomposition would not apply to them. This shows one of the advantages of Lebesgue integration.", ) Concretely this means that for any sequence of Lebesgue-integrable functions with |ƒn|p < ∞, satisfying the condition
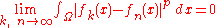
there exists a function ƒ(x) belonging to the vector space Lp(Ω) such that
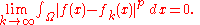
Imposing boundedness conditions not only on the function, but also on its derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s leads to Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s.
Hilbert spaces
Complete inner product spaces are known as Hilbert spaces, in honor of David HilbertDavid Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
.
The Hilbert space L2(Ω), with inner product given by
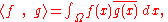
where
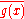denotes the complex conjugateComplex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
of g(x).For p ≠2, Lp(Ω) is not a Hilbert space. is a key case.
By definition, in a Hilbert space any Cauchy sequences converges to a limit. Conversely, finding a sequence of functions ƒn with desirable properties that approximates a given limit function, is equally crucial. Early analysis, in the guise of the Taylor approximation, established an approximation of differentiable function
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
s ƒ by polynomials. By the Stone–Weierstrass theorem, every continuous function on can be approximated as closely as desired by a polynomial. A similar approximation technique by trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s is commonly called Fourier expansion, and is much applied in engineering, see below. More generally, and more conceptually, the theorem yields a simple description of what "basic functions", or, in abstract Hilbert spaces, what basic vectors suffice to generate a Hilbert space H, in the sense that the closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of their span (i.e., finite linear combinations and limits of those) is the whole space. Such a set of functions is called a basis of H, its cardinality is known as the Hilbert dimension.A basis of a Hilbert space is not the same thing as a basis in the sense of linear algebra above. For distinction, the latter is then called a Hamel basis. Not only does the theorem exhibit suitable basis functions as sufficient for approximation purposes, together with the Gram-Schmidt process it also allows to construct a basis of orthogonal vectors
Orthogonal basis
In mathematics, particularly linear algebra, an orthogonal basis for an inner product space is a basis for whose vectors are mutually orthogonal...
. Such orthogonal bases are the Hilbert space generalization of the coordinate axes in finite-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
.
The solutions to various differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s can be interpreted in terms of Hilbert spaces. For example, a great many fields in physics and engineering lead to such equations and frequently solutions with particular physical properties are used as basis functions, often orthogonal. As an example from physics, the time-dependent Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
describes the change of physical properties in time, by means of a partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
whose solutions are called wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
s. Definite values for physical properties such as energy, or momentum, correspond to eigenvalues of a certain (linear) differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
and the associated wavefunctions are called eigenstates. The spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
decomposes a linear compact operator
Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
acting on functions in terms of these eigenfunctions and their eigenvalues.
Algebras over fields
Bilinear operator
In mathematics, a bilinear operator is a function combining elements of two vector spaces to yield an element of a third vector space that is linear in each of its arguments. Matrix multiplication is an example.-Definition:...
defining the multiplication of two vectors is an algebra over a field. Many algebras stem from functions on some geometrical object: since functions with values in a field can be multiplied, these entities form algebras. The Stone–Weierstrass theorem mentioned above, for example, relies on Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
s which are both Banach spaces and algebras.
Commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
makes great use of rings of polynomials
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
in one or several variables, introduced above. Their multiplication is both commutative and associative. These rings and their quotients
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
form the basis of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, because they are rings of functions of algebraic geometric objects.
Another crucial example are Lie algebras, which are neither commutative nor associative, but the failure to be so is limited by the constraints ([x, y] denotes the product of x and y):
- [
Anticommutativity
In mathematics, anticommutativity is the property of an operation that swapping the position of any two arguments negates the result. Anticommutative operations are widely used in algebra, geometry, mathematical analysis and, as a consequence, in physics: they are often called antisymmetric...
), and 0}} (Jacobi identity
Jacobi identity
In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
).
Examples include the vector space of n-by-n matrices, with [x, y] = xy − yx, the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
of two matrices, and R3, endowed with the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
.
The tensor algebra
Tensor algebra
In mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
T(V) is a formal way of adding products to any vector space V to obtain an algebra. As a vector space, it is spanned by symbols, called simple tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
s
- v1 ⊗ v2 ⊗ ... ⊗ v
The multiplication is given by concatenating such symbols, imposing the distributive law under addition, and requiring that scalar multiplication commute with the tensor product ⊗, much the same way as with the tensor product of two vector spaces introduced above. In general, there are no relations between and . Forcing two such elements to be equal leads to the symmetric algebra
Symmetric algebra
In mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
, whereas forcing v1 ⊗ v2 = − v2 ⊗ v1 yields the exterior algebra
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
.
When a field, F is explicitly stated, a common term used is .
Applications
Vector spaces have manifold applications as they occur in many circumstances, namely wherever functions with values in some field are involved. They provide a framework to deal with analytical and geometrical problems, or are used in the Fourier transform. This list is not exhaustive: many more applications exist, for example in optimizationOptimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
. The minimax theorem of game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
stating the existence of a unique payoff when all players play optimally can be formulated and proven using vector spaces methods. Representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
fruitfully transfers the good understanding of linear algebra and vector spaces to other mathematical domains such as group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
.
Distributions
A distribution (or generalized function) is a linear map assigning a number to each "test" function, typically a smooth functionSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
with compact support, in a continuous way: in the above terminology the space of distributions is the (continuous) dual of the test function space. The latter space is endowed with a topology that takes into account not only ƒ itself, but also all its higher derivatives. A standard example is the result of integrating a test function ƒ over some domain Ω:
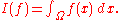
When Ω = {p}, the set consisting of a single point, this reduces to the Dirac distribution, denoted by δ, which associates to a test function ƒ its value at the p: δ(ƒ) = ƒ(p). Distributions are a powerful instrument to solve differential equations. Since all standard analytic notions such as derivatives are linear, they extend naturally to the space of distributions. Therefore the equation in question can be transferred to a distribution space, which is bigger than the underlying function space, so that more flexible methods are available for solving the equation. For example, Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
s and fundamental solution
Fundamental solution
In mathematics, a fundamental solution for a linear partial differential operator L is a formulation in the language of distribution theory of the older idea of a Green's function...
s are usually distributions rather than proper functions, and can then be used to find solutions of the equation with prescribed boundary conditions. The found solution can then in some cases be proven to be actually a true function, and a solution to the original equation (e.g., using the Lax–Milgram theorem, a consequence of the Riesz representation theorem
Riesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
).
Fourier analysis
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
into a sum of trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s forms a Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
, a technique much used in physics and engineering.Although the Fourier series is periodic, the technique can be applied to any L2 function on an interval by considering the function to be continued periodically outside the interval. See The underlying vector space is usually the Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
L2(0, 2π), for which the functions sin mx and cos mx (m an integer) form an orthogonal basis. The Fourier expansion of an L2 function f is
The coefficients am and bm are called Fourier coefficients of ƒ, and are calculated by the formulas
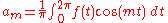, In physical terms the function is represented as a superposition
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
of sine waves and the coefficients give information about the function's frequency spectrum
Frequency spectrum
The frequency spectrum of a time-domain signal is a representation of that signal in the frequency domain. The frequency spectrum can be generated via a Fourier transform of the signal, and the resulting values are usually presented as amplitude and phase, both plotted versus frequency.Any signal...
. A complex-number form of Fourier series is also commonly used. The concrete formulae above are consequences of a more general mathematical duality
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
called Pontryagin duality
Pontryagin duality
In mathematics, specifically in harmonic analysis and the theory of topological groups, Pontryagin duality explains the general properties of the Fourier transform on locally compact groups, such as R, the circle or finite cyclic groups.-Introduction:...
. Applied to the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
R, it yields the classical Fourier transform; an application in physics are reciprocal lattice
Reciprocal lattice
In physics, the reciprocal lattice of a lattice is the lattice in which the Fourier transform of the spatial function of the original lattice is represented. This space is also known as momentum space or less commonly k-space, due to the relationship between the Pontryagin duals momentum and...
s, where the underlying group is a finite-dimensional real vector space endowed with the additional datum of a lattice encoding positions of atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
s in crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
s.
Fourier series are used to solve boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
s in partial differential equations. In 1822, Fourier
Joseph Fourier
Jean Baptiste Joseph Fourier was a French mathematician and physicist best known for initiating the investigation of Fourier series and their applications to problems of heat transfer and vibrations. The Fourier transform and Fourier's Law are also named in his honour...
first used this technique to solve the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
. A discrete version of the Fourier series can be used in sampling
Sampling (signal processing)
In signal processing, sampling is the reduction of a continuous signal to a discrete signal. A common example is the conversion of a sound wave to a sequence of samples ....
applications where the function value is known only at a finite number of equally spaced points. In this case the Fourier series is finite and its value is equal to the sampled values at all points. The set of coefficients is known as the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
(DFT) of the given sample sequence. The DFT is one of the key tools of digital signal processing
Digital signal processing
Digital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
, a field whose applications include radar
Radar
Radar is an object-detection system which uses radio waves to determine the range, altitude, direction, or speed of objects. It can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, weather formations, and terrain. The radar dish or antenna transmits pulses of radio...
, speech encoding
Speech encoding
Speech coding is the application of data compression of digital audio signals containing speech. Speech coding uses speech-specific parameter estimation using audio signal processing techniques to model the speech signal, combined with generic data compression algorithms to represent the resulting...
, image compression
Image compression
The objective of image compression is to reduce irrelevance and redundancy of the image data in order to be able to store or transmit data in an efficient form.- Lossy and lossless compression :...
. The JPEG
JPEG
In computing, JPEG . The degree of compression can be adjusted, allowing a selectable tradeoff between storage size and image quality. JPEG typically achieves 10:1 compression with little perceptible loss in image quality....
image format is an application of the closely related discrete cosine transform
Discrete cosine transform
A discrete cosine transform expresses a sequence of finitely many data points in terms of a sum of cosine functions oscillating at different frequencies. DCTs are important to numerous applications in science and engineering, from lossy compression of audio and images A discrete cosine transform...
.
The fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
is an algorithm for rapidly computing the discrete Fourier transform. It is used not only for calculating the Fourier coefficients but, using the convolution theorem
Convolution theorem
In mathematics, the convolution theorem states that under suitableconditions the Fourier transform of a convolution is the pointwise product of Fourier transforms. In other words, convolution in one domain equals point-wise multiplication in the other domain...
, also for computing the convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of two finite sequences. They in turn are applied in digital filter
Digital filter
In electronics, computer science and mathematics, a digital filter is a system that performs mathematical operations on a sampled, discrete-time signal to reduce or enhance certain aspects of that signal. This is in contrast to the other major type of electronic filter, the analog filter, which is...
s and as a rapid multiplication algorithm
Multiplication algorithm
A multiplication algorithm is an algorithm to multiply two numbers. Depending on the size of the numbers, different algorithms are in use...
for polynomials and large integers (Schönhage-Strassen algorithm
Schönhage-Strassen algorithm
The Schönhage–Strassen algorithm is an asymptotically fast multiplication algorithm for large integers. It was developed by Arnold Schönhage and Volker Strassen in 1971. The run-time bit complexity is, in Big O notation, O...
).
Differential geometry
The tangent plane to a surface at a point is naturally a vector space whose origin is identified with the point of contact. The tangent plane is the best linear approximationLinear approximation
In mathematics, a linear approximation is an approximation of a general function using a linear function . They are widely used in the method of finite differences to produce first order methods for solving or approximating solutions to equations.-Definition:Given a twice continuously...
, or linearization
Linearization
In mathematics and its applications, linearization refers to finding the linear approximation to a function at a given point. In the study of dynamical systems, linearization is a method for assessing the local stability of an equilibrium point of a system of nonlinear differential equations or...
, of a surface at a point.That is to say , the plane passing through the point of contact P such that the distance from a point P1 on the surface to the plane is infinitesimally small compared to the distance from P1 to P in the limit as P1 approaches P along the surface. Even in a three-dimensional Euclidean space, there is typically no natural way to prescribe a basis of the tangent plane, and so it is conceived of as an abstract vector space rather than a real coordinate space. The tangent space is the generalization to higher-dimensional differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
s.
Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s are manifolds whose tangent spaces are endowed with a suitable inner product. Derived therefrom, the Riemann curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
encodes all curvatures of a manifold in one object, which finds applications in general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, for example, where the Einstein curvature tensor describes the matter and energy content of space-time. The tangent space of a Lie group can be given naturally the structure of a Lie algebra and can be used to classify compact Lie groups.
Vector bundles
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X. More precisely, a vector bundle over X is a topological space E equipped with a continuous map
- π :
such that for every x in X, the fiber π−1(x) is a vector space. The case dim V = 1 is called a line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
. For any vector space V, the projection X × V → X makes the product X × V into a "trivial" vector bundle. Vector bundles over X are required to be locally a product of X and some (fixed) vector space V: for every x in X, there is a neighborhood U of x such that the restriction of π to π−1(U) is isomorphicThat is, there is a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
from π−1(U) to V × U which restricts to linear isomorphisms between fibers. to the trivial bundle U × V → U. Despite their locally trivial character, vector bundles may (depending on the shape of the underlying space X) be "twisted" in the large, i.e., the bundle need not be (globally isomorphic to) the trivial bundle For example, the Möbius strip
Möbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
can be seen as a line bundle over the circle S1 (by identifying open intervals with the real line). It is, however, different from the cylinder
Cylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
S1 × R, because the latter is orientable whereas the former is not.
Properties of certain vector bundles provide information about the underlying topological space. For example, the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
consists of the collection of tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
s parametrized by the points of a differentiable manifold. The tangent bundle of the circle S1 is globally isomorphic to S1 × R, since there is a global nonzero vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
on S1.A line bundle, such as the tangent bundle of S1 is trivial if and only if there is a section
Section (fiber bundle)
In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
that vanishes nowhere, see . The sections of the tangent bundle are just vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s. In contrast, by the hairy ball theorem
Hairy ball theorem
The hairy ball theorem of algebraic topology states that there is no nonvanishing continuous tangent vector field on an even-dimensional n-sphere. An ordinary sphere is a 2-sphere, so that this theorem will hold for an ordinary sphere...
, there is no (tangent) vector field on the 2-sphere S2 which is everywhere nonzero. K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
studies the isomorphism classes of all vector bundles over some topological space. In addition to deepening topological and geometrical insight, it has purely algebraic consequences, such as the classification of finite-dimensional real division algebra
Division algebra
In the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field, in which division is possible.- Definitions :...
s: R, C, the quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s H and the octonion
Octonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s.
The cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
of a differentiable manifold consists, at every point of the manifold, of the dual of the tangent space, the cotangent space
Cotangent space
In differential geometry, one can attach to every point x of a smooth manifold a vector space called the cotangent space at x. Typically, the cotangent space is defined as the dual space of the tangent space at x, although there are more direct definitions...
. Sections
Section (fiber bundle)
In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
of that bundle are known as differential one-form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s.
Modules
Modules are to ringsRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
what vector spaces are to fields. The very same axioms, applied to a ring R instead of a field F yield modules. The theory of modules, compared to vector spaces, is complicated by the presence of ring elements that do not have multiplicative inverse
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
s. For example, modules need not have bases, as the Z-module (i.e., abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
) Z/2Z
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
shows; those modules that do (including all vector spaces) are known as free module
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
s.
To see why the requirement that for every scalar there exist multiplicative inverse makes a difference, consider this: the fact that every vector space has a basis amounts to saying that every vector space is a free module. The proof of this fact fails for general modules over any ring(at least for modules of finite type) in the step "in every list b of linearly dependent vectors, it is possible to remove one vector from b without changing span of b". This does not hold in a general module, but holds in any vector space. So when we have a linearly dependent finite list of vectors that spans the whole vector space at hand (which must exist in a finite-dimensional vector space), we can remove one vector from the list and the list will still span the whole vector space. We can repeat this process until we get a basis; we cannot do this in general in a module. As it turns out, requiring that a module be over a field instead of a ring is a sufficient condition for this to hold.
Nevertheless, a vector space can be compactly defined as a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
which is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
with the elements being called vectors. The algebro-geometric interpretation of commutative rings via their spectrum
Spectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
allows the development of concepts such as locally free modules, the algebraic counterpart to vector bundles.
Affine and projective spaces
Roughly, affine spaces are vector spaces whose origin is not specified. More precisely, an affine space is a set with a free transitive vector space actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
. In particular, a vector space is an affine space over itself, by the map
If W is a vector space, then an affine subspace is a subset of W obtained by translating a linear subspace V by a fixed vector ; this space is denoted by x + V (it is a coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
of V in W) and consists of all vectors of the form for An important example is the space of solutions of a system of inhomogeneous linear equations
generalizing the homogeneous case b = 0 above. The space of solutions is the affine subspace x + V where x is a particular solution of the equation, and V is the space of solutions of the homogeneous equation (the nullspace of A).
The set of one-dimensional subspaces of a fixed finite-dimensional vector space V is known as projective space; it may be used to formalize the idea of parallel
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
lines intersecting at infinity. Grassmannians and flag manifold
Flag manifold
In mathematics, a generalized flag variety is a homogeneous space whose points are flags in a finite-dimensional vector space V over a field F. When F is the real or complex numbers, a generalized flag variety is a smooth or complex manifold, called a real or complex flag manifold...
s generalize this by parametrizing linear subspaces of fixed dimension k and flags of subspaces, respectively.
Convex analysis
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
, notably the real numbers, there are the added notions of convex analysis
Convex analysis
Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory....
, most basically a cone
Cone (linear algebra)
In linear algebra, a cone is a subset of a vector space that is closed under multiplication by positive scalars. In other words, a subset C of a real vector space V is a cone if and only if λx belongs to C for any x in C and any positive scalar λ of V .A cone is said...
, which allows only non-negative linear combinations, and a convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
, which allows only non-negative linear combinations that sum to 1. A convex set can be seen as the combinations of the axioms for an affine space and a cone, which is reflected in the standard space for it, the n-simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
, being the intersection of the affine hyperplane and orthant
Orthant
In geometry, an orthant or hyperoctant is the analogue in n-dimensional Euclidean space of a quadrant in the plane or an octant in three dimensions....
. Such spaces are particularly used in linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
.
In the language of universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
, a vector space is an algebra over the universal vector space K∞ of finite sequences of coefficients, corresponding to finite sums of vectors, while an affine space is an algebra over the universal affine hyperplane in here (of finite sequences summing to 1), a cone is an algebra over the universal orthant, and a convex set is an algebra over the universal simplex. This geometrizes the axioms in terms of "sums with (possible) restrictions on the coordinates".
Many concepts in linear algebra have analogs in convex analysis, including basic ones such as basis and span (such as in the form of convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
), and notably including duality (in the form of dual polyhedron
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
, dual cone, dual problem
Dual problem
In constrained optimization, it is often possible to convert the primal problem to a dual form, which is termed a dual problem. Usually dual problem refers to the Lagrangian dual problem but other dual problems are used, for example, the Wolfe dual problem and the Fenchel dual problem...
). Unlike linear algebra, however, where every vector space or affine space is isomorphic to the standard spaces, not every convex set or cone is isomorphic to the simplex or orthant. Rather, there is always a map from the simplex onto a polytope, given by generalized barycentric coordinates, and a dual map from a polytope into the orthant (of dimension equal to the number of faces) given by slack variable
Slack variable
In an optimization problem, a slack variable is a variable that is added to an inequality constraint to transform it to an equality. Introducing a slack variable replaces an inequality constraint with an equality constraint and a nonnegativity constraint....
s, but these are rarely isomorphisms – most polytopes are not a simplex or an orthant.
See also
- Cartesian coordinate systemCartesian coordinate systemA Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
- Euclidean vector, for vectors in physics
- Gyrovector spaceGyrovector spaceA gyrovector space is a mathematical concept for studying hyperbolic geometry in analogy to the way vector spaces are used in Euclidean geometry. This vector-based approach has been developed by Abraham Albert Ungar from the late 1980s onwards...
- Graded vector spaceGraded vector spaceIn mathematics, a graded vector space is a type of vector space that includes the extra structure of gradation, which is a decomposition of the vector space into a direct sum of vector subspaces.-N-graded vector spaces:...
- Metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
- P-vector
- Riesz–Fischer theoremRiesz–Fischer theoremIn mathematics, the Riesz–Fischer theorem in real analysis refers to a number of closely related results concerning the properties of the space L2 of square integrable functions...
- Vector spaces without fieldsVector spaces without fieldsIn mathematics, the conventional definition of the concept of vector space relies upon the algebraic concept of a field. This article treats an algebraic definition that does not require that concept. If vector spaces are redefined as algebras as below, no preliminary introduction of fields is...
- Space (mathematics)
Linear algebra
Historical references
, reprint:Further references
External links
- A lecture about fundamental concepts related to vector spaces (given at MIT)
- A graphical simulator for the concepts of span, linear dependency, base and dimension