
Interval (mathematics)
Encyclopedia
In mathematics
, a (real) interval is a set of real number
s with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them. Other examples of intervals are the set of all real numbers , the set of all negative real numbers, and the empty set
, the set of all negative real numbers, and the empty set
.
Real intervals play an important role in the theory of integration
, because they are the simplest sets whose "size" or "measure" or "length" is easy to define. The concept of measure can then be extended to more complicated sets of real numbers, leading to the Borel measure and eventually to the Lebesgue measure
.
Intervals are central to interval arithmetic
, a general numerical computing technique that automatically provides guaranteed enclosures for arbitrary formulas, even in the presence of uncertainties, mathematical approximations, and arithmetic roundoff.
 and
and  , including
, including  and
and  , is often denoted
, is often denoted 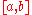 . The two numbers are called the endpoints of the interval. In countries where numbers are written with a decimal comma, a semicolon
. The two numbers are called the endpoints of the interval. In countries where numbers are written with a decimal comma, a semicolon
may be used as a separator, to avoid ambiguity.
ISO 31-11
. Thus, in set builder notation,
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a (real) interval is a set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them. Other examples of intervals are the set of all real numbers
 , the set of all negative real numbers, and the empty set
, the set of all negative real numbers, and the empty setEmpty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
.
Real intervals play an important role in the theory of integration
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
, because they are the simplest sets whose "size" or "measure" or "length" is easy to define. The concept of measure can then be extended to more complicated sets of real numbers, leading to the Borel measure and eventually to the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
.
Intervals are central to interval arithmetic
Interval arithmetic
Interval arithmetic, interval mathematics, interval analysis, or interval computation, is a method developed by mathematicians since the 1950s and 1960s as an approach to putting bounds on rounding errors and measurement errors in mathematical computation and thus developing numerical methods that...
, a general numerical computing technique that automatically provides guaranteed enclosures for arbitrary formulas, even in the presence of uncertainties, mathematical approximations, and arithmetic roundoff.
Notations for intervals
The interval of numbers between and
and  , including
, including  and
and  , is often denoted
, is often denoted 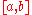 . The two numbers are called the endpoints of the interval. In countries where numbers are written with a decimal comma, a semicolon
. The two numbers are called the endpoints of the interval. In countries where numbers are written with a decimal comma, a semicolonSemicolon
The semicolon is a punctuation mark with several uses. The Italian printer Aldus Manutius the Elder established the practice of using the semicolon to separate words of opposed meaning and to indicate interdependent statements. "The first printed semicolon was the work of ... Aldus Manutius"...
may be used as a separator, to avoid ambiguity.
Excluding the endpoints
To indicate that one of the endpoints is to be excluded from the set, the corresponding square bracket can be either replaced with a parenthesis, or reversed. Both notations are described in International standardInternational standard
International standards are standards developed by international standards organizations. International standards are available for consideration and use, worldwide...
ISO 31-11
ISO 31-11
ISO 31-11 was the part of international standard ISO 31 that defines mathematical signs and symbols for use in physical sciences and technology...
. Thus, in set builder notation,
-

Note that ,
,  , and
, and  denote the empty set, whereas
denote the empty set, whereas  denotes the set
denotes the set  . When
. When  , all four notations are usually assumed to represent the empty set.
, all four notations are usually assumed to represent the empty set.
Both notations may overlap with other uses of parentheses and brackets in mathematics. For instance, the notation is often used to denote an ordered pairTupleIn mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
is often used to denote an ordered pairTupleIn mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
in set theory, the coordinates of a pointPoint (geometry)In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
or vector in analytic geometryAnalytic geometryAnalytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
and linear algebraLinear algebraLinear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, or (sometimes) a complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
in algebraAlgebraAlgebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
. The notation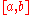 too is occasionally used for ordered pairs, especially in computer scienceComputer scienceComputer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
too is occasionally used for ordered pairs, especially in computer scienceComputer scienceComputer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
.
Some authors use to denote the complement of the interval
to denote the complement of the interval 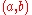 ; namely, the set of all real numbers that are either less than or equal to a, or greater than or equal to b.
; namely, the set of all real numbers that are either less than or equal to a, or greater than or equal to b.
Infinite endpoints
In both styles of notation, one may use an infinite endpoint to indicate that there is no bound in that direction. Specifically, one may use or
or  (or both). For example,
(or both). For example,  is the set of all positive real numbers, and
is the set of all positive real numbers, and  is the set of real numbers.
is the set of real numbers.
The notations ,
,  ,
,  , and
, and  are ambiguous. For authors who define intervals as subsets of the real numbers, those notations are either meaningless, or equivalent to the open variants. In the latter case, the interval comprising all real numbers is both open and closed,
are ambiguous. For authors who define intervals as subsets of the real numbers, those notations are either meaningless, or equivalent to the open variants. In the latter case, the interval comprising all real numbers is both open and closed,  .
.
On the extended real number lineExtended real number lineIn mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
the intervals are all different as this includes and elements. For example means the extended real numbers excluding only .
Integer intervals
The notation when and are integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, or , or just is sometimes used to indicate the interval of all integers between and , including both. This notation is used in some programming languageProgramming languageA programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s; in Pascal, for example, it is used to define the set of valid indicesIndex (mathematics)The word index is used in variety of senses in mathematics.- General :* In perhaps the most frequent sense, an index is a number or other symbol that indicates the location of a variable in a list or array of numbers or other mathematical objects. This type of index is usually written as a...
of a vectorArray data typeIn computer science, an array type is a data type that is meant to describe a collection of elements , each selected by one or more indices that can be computed at run time by the program. Such a collection is usually called an array variable, array value, or simply array...
.
An integer interval that has a finite lower or upper endpoint always includes that endpoint. Therefore, the exclusion of endpoints can be explicitly denoted by writing , , or . Alternate-bracket notations like or are rarely used for integer intervals.
Terminology
An open interval does not include its endpoints, and is indicated with parentheses. For example means greater than and less than . Conversely, a closed interval includes its endpoints, and is denoted with square brackets. For example means greater than or equal to and less than or equal to .
A degenerate interval is any set consisting of a single real number. Some authors include the empty set in this definition. An interval that is neither empty nor degenerate is said to be proper, and has infinitely many elements.
An interval is said to be left-bounded or right-bounded if there is some real number that is, respectively, smaller than or larger than all its elements. An interval is said to be bounded if it is both left- and right-bounded; and is said to be unbounded otherwise. Intervals that are bounded at only one end are said to be half-bounded. The empty set is bounded, and the set of all reals is the only interval that is unbounded at both ends. Bounded intervals are also commonly known as finite intervals.
Bounded intervals are bounded setBounded setIn mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
s, in the sense that their diameterDiameterIn geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
(which is equal to the absolute differenceAbsolute differenceThe absolute difference of two real numbers x, y is given by |x − y|, the absolute value of their difference. It describes the distance on the real line between the points corresponding to x and y...
between the endpoints) is finite. The diameter may be called the length, width, measure, or size of the interval. The size of unbounded intervals is usually defined as , and the size of the empty interval may be defined as or left undefined.
The centre of bounded interval with endpoints and is , and its radius is the half-length . These concepts are undefined for empty or unbounded intervals.
An interval is said to be left-open if and only if it has no minimum (an element that is smaller than all other elements); right-open if it has no maximum; and open if it has both properties. The interval , for example, is left-closed and right-open. The empty set and the set of all reals are open intervals, while the set of non-negative reals, for example, is a right-open but not left-open interval. The open intervals coincide with the open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s of the real line in its standard topology.
An interval is said to be left-closed if it has a minimum element, right-closed if it has a maximum, and simply closed if it has both. These definitions are usually extended to include the empty set and to the (left- or right-) unbounded intervals, so that the closed intervals coincide with closed setClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
s in that topology.
The interior of an interval is the largest open interval that is contained in ; it is also the set of points in which are not endpoints of . The closure of is the smallest closed interval that contains ; which is also the set augmented with its finite endpoints.
For any set of real numbers, the interval enclosure or interval span of is the unique interval that contains and does not properly contain any other interval that also contains .
Classification of intervals
The intervals of real numbers can be classified into eleven different types, listed below; where and
and  are real numbers, with
are real numbers, with  :
:
- empty:

- degenerate:

- proper and bounded:
- open:
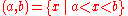
- closed:

- left-closed, right-open:

- left-open, right-closed:

- open:
- left-bounded and right-unbounded:
- left-open:

- left-closed:
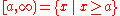
- left-open:
- left-unbounded and right-bounded:
- right-open:

- right-closed:

- right-open:
- unbounded at both ends:

Intervals of the extended real line
In some contexts, an interval may be defined as a subset of the extended real numbersExtended real number lineIn mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
, the set of all real numbers augmented with and
and  .
.
In this interpretation, the notations ,
,  ,
,  , and
, and  are all meaningful and distinct. In particular,
are all meaningful and distinct. In particular,  denotes the set of all ordinary real numbers, while
denotes the set of all ordinary real numbers, while  denotes the extended reals.
denotes the extended reals.
This choice affects some of the above definitions and terminology. For instance, the interval is closed in the realm of ordinary reals, but not in the realm of the extended reals.
is closed in the realm of ordinary reals, but not in the realm of the extended reals.
Properties of intervals
The intervals are precisely the connectedConnectednessIn mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...
subsets of . It follows that the image of an interval by any continuous function is also an interval. This is one formulation of the intermediate value theoremIntermediate value theoremIn mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
. It follows that the image of an interval by any continuous function is also an interval. This is one formulation of the intermediate value theoremIntermediate value theoremIn mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
.
The intervals are also the convex subsetConvex setIn Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
s of . The interval enclosure of a subset
. The interval enclosure of a subset  is also the convex hullConvex hullIn mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
is also the convex hullConvex hullIn mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of .
.
The intersection of any collection of intervals is always an interval. The union of two intervals is an interval if and only if they have a non-empty intersection or an open end-point of one interval is a closed end-point of the other (e.g.,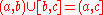 ).
).
If is viewed as a metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
is viewed as a metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, its open balls are the open bounded sets , and its closed balls are the closed bounded sets
, and its closed balls are the closed bounded sets  .
.
Any element of an interval
of an interval  defines a partition of
defines a partition of  into three disjoint intervals
into three disjoint intervals  : respectively, the elements of
: respectively, the elements of  that are less than
that are less than  , the singleton
, the singleton  , and the elements that are greater than
, and the elements that are greater than  . The parts
. The parts 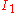 and
and  are both non-empty (and have non-empty interiors) if and only if
are both non-empty (and have non-empty interiors) if and only if  is in the interior of
is in the interior of  . This is an interval version of the trichotomy principle.
. This is an interval version of the trichotomy principle.
Dyadic intervals
A dyadic interval is a bounded real interval whose endpoints are and
and  , where
, where 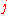 and
and  are integers. Depending on the context, either endpoint may or may not be included in the interval.
are integers. Depending on the context, either endpoint may or may not be included in the interval.
Dyadic intervals have some nice properties, such as the following:
- The length of a dyadic interval is always an integer power of two.
- Every dyadic interval is contained in exactly one "parent" dyadic interval of twice the length.
- Every dyadic interval is spanned by two "child" dyadic intervals of half the length.
- If two dyadic intervals overlap, then one of them must be a subset of the other.
The dyadic intervals thus have a structure very similar to an infinite binary treeBinary treeIn computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
.
Dyadic intervals are relevant to several areas of numerical analysis, including adaptive mesh refinementAdaptive mesh refinementIn numerical analysis, adaptive mesh refinement is a method of adaptive meshing. Central to any Eulerian method is the manner in which it discretizes the continuous domain of interest into a grid of many individual elements...
, multigrid methods, and
wavelet analysisWaveletA wavelet is a wave-like oscillation with an amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have...
.
Multi-dimensional intervals
In many contexts, an -dimensional interval is defined as a subset of
-dimensional interval is defined as a subset of  that is the Cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
that is the Cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of intervals,
intervals,  , one on each coordinate axis.
, one on each coordinate axis.
For , this generally defines a rectangleRectangleIn Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
, this generally defines a rectangleRectangleIn Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
whose sides are parallel to the coordinate axes; for , it defines an axis-aligned rectangular box.
, it defines an axis-aligned rectangular box.
A facet of such an interval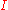 is the result of replacing any non-degenerate interval factor
is the result of replacing any non-degenerate interval factor 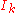 by a degenerate interval consisting of a finite endpoint of
by a degenerate interval consisting of a finite endpoint of  . The faces of
. The faces of 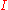 comprise
comprise 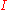 itself and all faces of its facets. The corners of
itself and all faces of its facets. The corners of 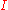 are the faces that consist of a single point of
are the faces that consist of a single point of  .
.
Complex intervals
Intervals of complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s can be defined as regions of the complex planeComplex planeIn mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, either rectangularRectangleIn Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
or circularDisk (mathematics)In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
.
See also
- Inequality
- Interval arithmeticInterval arithmeticInterval arithmetic, interval mathematics, interval analysis, or interval computation, is a method developed by mathematicians since the 1950s and 1960s as an approach to putting bounds on rounding errors and measurement errors in mathematical computation and thus developing numerical methods that...
- Interval graphInterval graphIn graph theory, an interval graph is the intersection graph of a multiset of intervals on the real line. It has one vertex for each interval in the set, and an edge between every pair of vertices corresponding to intervals that intersect.-Definition:...
- Interval finite elementInterval finite elementThe interval finite element method is a finite element method that uses interval parameters. Interval FEM can be applied in situations where it is not possible to get reliable probabilistic characteristics of the structure. This is important in concrete structures, wood structures, geomechanics,...
External links
- A Lucid Interval by Brian Hayes: An American Scientist article provides an introduction.
- Interval Notation Basics
- Interval computations website
- Interval computations research centers
- Interval Notation by George Beck, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
.
- empty:

