
Curve
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a curve (also called a curved line in older texts) is, generally speaking, an object similar to a line
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
but which is not required to be straight
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
. This entails that a line
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
is a special case of curve, namely a curve with null curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
.
Often curves in two-dimensional (plane curves) or three-dimensional (space curves) Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
are of interest.
Different disciplines within mathematics have given the term different meanings depending on the area of study, so the precise meaning depends on context. However many of these meanings are special instances of the definition which follows. A curve is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
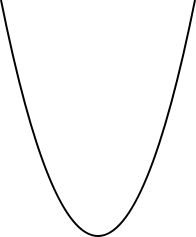
which is locally homeomorphic to a line. In every day language, this means that a curve is a set of points which, near each of its points, looks like a line, up to a deformation. A simple example of a curve is the parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
, shown to the right. A large number of other curves have been studied in multiple mathematical fields.
The term curve has several meanings in non-mathematical language as well. For example, it can be almost synonymous with mathematical function (as in learning curve
Learning curve
A learning curve is a graphical representation of the changing rate of learning for a given activity or tool. Typically, the increase in retention of information is sharpest after the initial attempts, and then gradually evens out, meaning that less and less new information is retained after each...
), or graph of a function
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
(as in Phillips curve
Phillips curve
In economics, the Phillips curve is a historical inverse relationship between the rate of unemployment and the rate of inflation in an economy. Stated simply, the lower the unemployment in an economy, the higher the rate of inflation...
).
An arc
Arc (geometry)
In geometry, an arc is a closed segment of a differentiable curve in the two-dimensional plane; for example, a circular arc is a segment of the circumference of a circle...
or segment of a curve is a part of a curve that is bounded by two distinct end points and contains every point on the curve between its end points. Depending on how the arc is defined, either of the two end points may or may not be part of it. When the arc is straight, it is typically called a line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
.
History

times. Curves, or at least their graphical representations, are simple to create, for example by a stick in the sand on a beach.
Historically, the term "line" was used in place of the more modern term "curve". Hence the phrases "straight line" and "right line" were used to distinguish what are today called lines from "curved lines". For example, in Book I of Euclid's Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
, a line is defined as a "breadthless length" (Def. 2), while a straight line is defined as "a line that lies evenly with the points on itself" (Def. 4). Euclid's idea of a line is perhaps clarified by the statement "The extremities of a line are points," (Def. 3). Later commentators further classified lines according to various schemes. For example:
- Composite lines (lines forming an angle)
- Incomposite lines
- Determinate (lines that do not extend indefinitely, such as the circle)
- Indeterminate (lines that extend indefinitely, such as the straight line and the parabola)
Compass and straightedge
Compass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass....
construction.
These curves include:
- The conic sectionConic sectionIn mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
s, deeply studied by Apollonius of PergaApollonius of PergaApollonius of Perga [Pergaeus] was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Isaac Newton, and René Descartes... - The cissoid of DioclesCissoid of DioclesIn geometry, the cissoid of Diocles is a cubic plane curve notable for the property that it can be used to construct two mean proportionals to a given ratio. In particular, it can be used to double a cube. It can be defined as the cissoid of a circle and a line tangent to it with respect to the...
, studied by DioclesDiocles (mathematician)Diocles was a Greek mathematician and geometer.- Life and work :Although little is known about the life of Diocles, it is known that he was a contemporary of Apollonius and that he flourished sometime around the end of the 3rd century BC and the beginning of the 2nd century BC.Diocles is thought...
and use a method to double the cubeDoubling the cubeDoubling the cube is one of the three most famous geometric problems unsolvable by compass and straightedge construction...
. - The conchoid of Nicomedes, studied by NicomedesNicomedes (mathematician)Nicomedes was an ancient Greek mathematician.- Life and work :Almost nothing is known about his life apart from references in his works. We know that he lived around the time of Eratosthenes or after, because he criticized Eratosthenes' method of doubling the cube...
as a method to both double the cube and to trisect an angleAngle trisectionAngle trisection is a classic problem of compass and straightedge constructions of ancient Greek mathematics. It concerns construction of an angle equal to one-third of a given arbitrary angle, using only two tools: an un-marked straightedge, and a compass....
. - The Archimedean spiralArchimedean spiralThe Archimedean spiral is a spiral named after the 3rd century BC Greek mathematician Archimedes. It is the locus of points corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line which rotates with constant angular velocity...
, studied by ArchimedesArchimedesArchimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
as a method to trisect an angle and square the circleSquaring the circleSquaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedge...
. - The spiric sectionSpiric sectionIn geometry, a spiric section, sometimes called a spiric of Perseus, is a quartic plane curve defined by equations of the form^2=dx^2+ey^2+f....
s, sections of toriTorusIn geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
studied by PerseusPerseus (geometer)Perseus was an ancient Greek geometer, who invented the concept of spiric sections, in analogy to the conic sections studied by Apollonius of Perga....
as sections of cones had been studied by Apollonius.
A fundamental advance in theory of curves was the advent of analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
in the seventeenth century. This enabled a curve to be described using an equation rather than an elaborate geometrical construction. This not only allowed new curves to be defined and studied, but it enabled a formal distinction to be made between curves that can be defined using algebraic equations, algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
s, and those that cannot, transcendental curve
Transcendental curve
In mathematics, a transcendental curve is a curve that is not an algebraic curve. Here for a curve C what matters is the point set underlying C, not a given parametrisation...
s. Previously, curves had been described as "geometrical" or "mechanical" according to how they were, or supposedly could be, generated.
Conic sections were applied in astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
by Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
.
Newton also worked on an early example in the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
. Solutions to variational problems, such as the brachistochrone and tautochrone questions, introduced properties of curves in new ways (in this case, the cycloid
Cycloid
A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
). The catenary
Catenary
In physics and geometry, the catenary is the curve that an idealised hanging chain or cable assumes when supported at its ends and acted on only by its own weight. The curve is the graph of the hyperbolic cosine function, and has a U-like shape, superficially similar in appearance to a parabola...
gets its name as the solution to the problem of a hanging chain, the sort of question that became routinely accessible by means of differential calculus
Differential calculus
In mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....
.
In the eighteenth century came the beginnings of the theory of plane algebraic curves, in general. Newton had studied the cubic curves, in the general description of the real points into 'ovals'. The statement of Bézout's theorem
Bézout's theorem
Bézout's theorem is a statement in algebraic geometry concerning the number of common points, or intersection points, of two plane algebraic curves. The theorem claims that the number of common points of two such curves X and Y is equal to the product of their degrees...
showed a number of aspects which were not directly accessible to the geometry of the time, to do with singular points and complex solutions.
From the nineteenth century there is not a separate curve theory, but rather the appearance of curves as the one-dimensional aspect of projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
, and differential geometry; and later topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, when for example the Jordan curve theorem
Jordan curve theorem
In topology, a Jordan curve is a non-self-intersecting continuous loop in the plane, and another name for a Jordan curve is a "simple closed curve"...
was understood to lie quite deep, as well as being required in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
. The era of the space-filling curve
Space-filling curve
In mathematical analysis, a space-filling curve is a curve whose range contains the entire 2-dimensional unit square...
s finally provoked the modern definitions of curve.
Topology
In topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a curve is defined as follows. Let
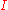 be an interval
be an intervalInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s (i.e. a non-empty connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of
 ). Then a curve
). Then a curve 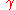 is a continuous mapping
is a continuous mappingMap (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
 , where
, where  is a topological space
is a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
.
- The curve
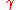 is said to be simple, or a Jordan arc, if it is injective, i.e. if for all
is said to be simple, or a Jordan arc, if it is injective, i.e. if for all  ,
, 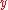 in
in 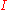 , we have
, we have 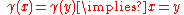 . If
. If 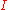 is a closed bounded interval
is a closed bounded interval 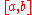 , we also allow the possibility
, we also allow the possibility 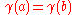 (this convention makes it possible to talk about "closed" simple curves, see below).
(this convention makes it possible to talk about "closed" simple curves, see below).
In other words this curve "does not cross itself and has no missing points".
- If
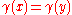 for some
for some 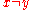 (other than the extremities of
(other than the extremities of 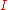 ), then
), then 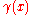 is called a double (or multiple) point of the curve.
is called a double (or multiple) point of the curve.
- A curve
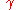 is said to be closed or a loop if
is said to be closed or a loop if  and if
and if 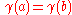 . A closed curve is thus a continuous mapping of the circle
. A closed curve is thus a continuous mapping of the circle 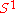 ; a simple closed curve is also called a Jordan curve. The Jordan curve theoremJordan curve theoremIn topology, a Jordan curve is a non-self-intersecting continuous loop in the plane, and another name for a Jordan curve is a "simple closed curve"...
; a simple closed curve is also called a Jordan curve. The Jordan curve theoremJordan curve theoremIn topology, a Jordan curve is a non-self-intersecting continuous loop in the plane, and another name for a Jordan curve is a "simple closed curve"...
states that such curves divide the plane into an "interior" and an "exterior".
A plane curvePlane curveIn mathematics, a plane curve is a curve in a Euclidean plane . The most frequently studied cases are smooth plane curves , and algebraic plane curves....
is a curve for which X is the Euclidean plane—these are the examples first encountered—or in some cases the projective planeProjective planeIn mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
. A space curve is a curve for which X is of three dimensions, usually Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
; a skew curve is a space curve which lies in no plane. These definitions also apply to algebraic curveAlgebraic curveIn algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
s (see below). However, in the case of algebraic curves it is very common not to restrict the curve to having points only defined over the real numbers.
This definition of curve captures our intuitive notion of a curve as a connected, continuous geometric figure that is "like" a line, without thickness and drawn without interruption, although it also includes figures that can hardly be called curves in common usage. For example, the image of a curve can cover a squareSquare (geometry)In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
in the plane (space-filling curveSpace-filling curveIn mathematical analysis, a space-filling curve is a curve whose range contains the entire 2-dimensional unit square...
). The image of simple plane curve can have Hausdorff dimensionHausdorff dimensionthumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
bigger than one (see Koch snowflakeKoch snowflakeThe Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described...
) and even positive Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
(the last example can be obtained by small variation of the Peano curve construction). The dragon curveDragon curveA dragon curve is any member of a family of self-similar fractal curves, which can be approximated by recursive methods such as Lindenmayer systems.-Heighway dragon:...
is another unusual example.
Conventions and terminology
The distinction between a curve and its imageImage (mathematics)In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
is important. Two distinct curves may have the same image. For example, a line segmentLine segmentIn geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
can be traced out at different speeds, or a circle can be traversed a different number of times. Many times, however, we are just interested in the image of the curve. It is important to pay attention to context and convention in reading.
Terminology is also not uniform. Often, topologists use the term "pathPath (topology)In mathematics, a path in a topological space X is a continuous map f from the unit interval I = [0,1] to XThe initial point of the path is f and the terminal point is f. One often speaks of a "path from x to y" where x and y are the initial and terminal points of the path...
" for what we are calling a curve, and "curve" for what we are calling the image of a curve. The term "curve" is more common in vector calculus and differential geometry.
Lengths of curves
If is a metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
is a metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
with metric , then we can define the length of a curve
, then we can define the length of a curve  by
by
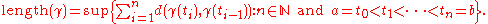
where the sup is over all and all partitions
and all partitions  of
of 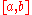 .
.
A is a curve with finite length.
A parametrizationParametric equationIn mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
of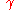 is called natural (or unit speed or parametrised by arc length) if for any
is called natural (or unit speed or parametrised by arc length) if for any 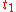 ,
,  in
in 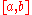 , we have
, we have
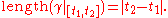
If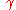 is a Lipschitz-continuousLipschitz continuityIn mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
is a Lipschitz-continuousLipschitz continuityIn mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
function, then it is automatically rectifiable. Moreover, in this case, one can define the speed (or metric derivativeMetric derivativeIn mathematics, the metric derivative is a notion of derivative appropriate to parametrized paths in metric spaces. It generalizes the notion of "speed" or "absolute velocity" to spaces which have a notion of distance but not direction .-Definition:Let be a metric space...
) of at
at 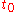 as
as

and then

In particular, if is an Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
is an Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
and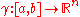 is differentiable then
is differentiable then

Differential geometry
While the first examples of curves that are met are mostly plane curves (that is, in everyday words, curved lines in two-dimensional space), there are obvious examples such as the helixHelixA helix is a type of smooth space curve, i.e. a curve in three-dimensional space. It has the property that the tangent line at any point makes a constant angle with a fixed line called the axis. Examples of helixes are coil springs and the handrails of spiral staircases. A "filled-in" helix – for...
which exist naturally in three dimensions. The needs of geometry, and also for example classical mechanicsClassical mechanicsIn physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
are to have a notion of curve in space of any number of dimensions. In general relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, a world lineWorld lineIn physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
is a curve in spacetimeSpacetimeIn physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
.
If is a differentiable manifoldDifferentiable manifoldA differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
is a differentiable manifoldDifferentiable manifoldA differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
, then we can define the notion of differentiable curve in . This general idea is enough to cover many of the applications of curves in mathematics. From a local point of view one can take
. This general idea is enough to cover many of the applications of curves in mathematics. From a local point of view one can take  to be Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
to be Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. On the other hand it is useful to be more general, in that (for example) it is possible to define the tangent vectorDifferential geometry of curvesDifferential geometry of curves is the branch of geometry that dealswith smooth curves in the plane and in the Euclidean space by methods of differential and integral calculus....
s to by means of this notion of curve.
by means of this notion of curve.
If is a smooth manifold, a smooth curve in
is a smooth manifold, a smooth curve in  is a smooth map
is a smooth map
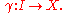
This is a basic notion. There are less and more restricted ideas, too. If is a
is a 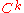 manifold (i.e., a manifold whose charts are
manifold (i.e., a manifold whose charts are 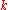 times continuously differentiable), then a
times continuously differentiable), then a  curve in
curve in  is such a curve which is only assumed to be
is such a curve which is only assumed to be  (i.e.
(i.e.  times continuously differentiable). If
times continuously differentiable). If  is an analytic manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
is an analytic manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
(i.e. infinitely differentiable and charts are expressible as power series), and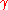 is an analytic map, then
is an analytic map, then 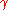 is said to be an analytic curve.
is said to be an analytic curve.
A differentiable curve is said to be regular if its derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
never vanishes. (In words, a regular curve never slows to a stop or backtracks on itself.) Two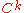 differentiable curves
differentiable curves
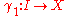 and
and
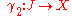
are said to be equivalent if there is a bijectiveBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
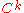 map
map
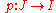
such that the inverse map
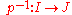
is also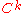 , and
, and
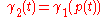
for all . The map
. The map 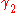 is called a reparametrisation of
is called a reparametrisation of 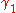 ; and this makes an equivalence relationEquivalence relationIn mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
; and this makes an equivalence relationEquivalence relationIn mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on the set of all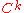 differentiable curves in
differentiable curves in  . A
. A 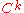 arc is an equivalence class of
arc is an equivalence class of 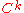 curves under the relation of reparametrisation.
curves under the relation of reparametrisation.
Algebraic curve
Algebraic curves are the curves considered in algebraic geometryAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. A plane algebraic curve is the locus of points f(x, y) = 0, where f(x, y) is a polynomial in two variables defined over some field F. Algebraic geometry normally looks at such curves in the context of algebraically closed fieldAlgebraically closed fieldIn mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
s. If K is the algebraic closureAlgebraic closureIn mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of F, and C is a curve defined by a polynomial f(x, y) defined over F, the points of the curve defined over F, consisting of pairs (a, b) with a and b in F, can be denoted C(F); the full curve itself being C(K).
Algebraic curves can also be space curves, or curves in even higher dimensions, obtained as the intersection (common solution set) of more than one polynomial equation in more than two variables. By eliminating variables by means of the resultant, these can be reduced to plane algebraic curves, which however may introduce singularities such as cuspCusp (singularity)In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....
s or double points. We may also consider these curves to have points defined in the projective planeProjective planeIn mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
; if
f(x, y) = 0 then if x = u/w and y = v/w, and n is the total degree of f, then by expanding out wnf(u/w, v/w) = 0 we obtain g(u, v, w) = 0, where g is homogeneousHomogeneous polynomialIn mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
of degree n. An example is the Fermat curveFermat curveIn mathematics, the Fermat curve is the algebraic curve in the complex projective plane defined in homogeneous coordinates by the Fermat equationX^n + Y^n = Z^n.\ Therefore in terms of the affine plane its equation is...
un + vn = wn, which has an affine form xn + yn = 1.
Important examples of algebraic curves are the conics, which are nonsingular curves of degree two and genusGenus (mathematics)In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
zero, and elliptic curveElliptic curveIn mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s, which are nonsingular curves of genus one studied in number theoryNumber theoryNumber theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
and which have important applications to cryptographyCryptographyCryptography is the practice and study of techniques for secure communication in the presence of third parties...
. Because algebraic curves in fields of characteristicCharacteristic (algebra)In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
zero are most often studied over the complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, algbebraic curves in algebraic geometry look like realReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
surfaces. Looking at them projectively, if we have a nonsingular curve in n dimensions, we obtain a picture in the complex projective space of dimension n, which corresponds to a real manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
of dimension 2n, in which the curve is an embedded smooth and compact surface with a certain number of holes in it, the genus. In fact, non-singular complex projective algebraic curves are compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Riemann surfaceRiemann surfaceIn mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s.
See also
- CurvatureCurvatureIn mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
- Curve orientationCurve orientationIn mathematics, a positively oriented curve is a planar simple closed curve such that when traveling on it one always has the curve interior to the left...
- Curves in differential geometry
- Curve sketchingCurve sketchingIn geometry, curve sketching includes techniques that can used to produce a rough idea of overall shape of a plane curve given its equation without computing the large numbers of points required for a detailed plot...
- Differential geometry of curvesDifferential geometry of curvesDifferential geometry of curves is the branch of geometry that dealswith smooth curves in the plane and in the Euclidean space by methods of differential and integral calculus....
- French curveFrench curveA French curve is a template made out of metal, wood or plastic composed of many different curves. It is used in manual drafting to draw smooth curves of varying radii....
- Gallery of curvesGallery of curves-Curves in art:-External links:*...
- List of curves
- List of curve topics
- Osculating circleOsculating circleIn differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point p on the curve has been traditionally defined as the circle passing through p and a pair of additional points on the curve infinitesimally close to p...
- Parametric surfaceParametric surfaceA parametric surface is a surface in the Euclidean space R3 which is defined by a parametric equation with two parameters. Parametric representation is the most general way to specify a surface. Surfaces that occur in two of the main theorems of vector calculus, Stokes' theorem and the divergence...
- Path (topology)Path (topology)In mathematics, a path in a topological space X is a continuous map f from the unit interval I = [0,1] to XThe initial point of the path is f and the terminal point is f. One often speaks of a "path from x to y" where x and y are the initial and terminal points of the path...
- Position vector
- Vector-valued functionVector-valued functionA vector-valued function also referred to as a vector function is a mathematical function of one or more variables whose range is a set of multidimensional vectors or infinite-dimensional vectors. The input of a vector-valued function could be a scalar or a vector...
External links
- Famous Curves Index, School of Mathematics and Statistics, University of St Andrews, Scotland
- Mathematical curves A collection of 874 two-dimensional mathematical curves
- http://faculty.evansville.edu/ck6/Gallery/Introduction.html Gallery of Space Curves Made from Circles, includes animations by Peter Moses
- http://faculty.evansville.edu/ck6/GalleryTwo/Introduction2.html Gallery of Bishop Curves and Other Sperical Curves, includes animations by Peter Moses
- YAN Kun. Research on adaptive connection equation in discontinuous area of data curve. DOI:10.3969/j.issn.1004-2903.2011.01.018
- Curvature

