Function composition
Encyclopedia
In mathematics
, function composition is the application of one function
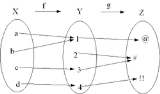
to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f(x) instead of x. Intuitively, if z is a function g of y and y is a function f of x, then z is a function of x.
Thus one obtains a composite function : defined by for all x in X. The notation is read as "g circle f", or "g composed with f", "g after f", "g following f", or just "g of f".
The composition of functions is always associative. That is, if f, g, and h are three functions with suitably chosen domain
s and codomain
s, then , where the parentheses serve to indicate that composition is to be performed first for the parenthesized functions. Since there is no distinction between the choices of placement of parentheses, they may be safely left off.
The functions g and f are said to commute with each other if . In general, composition of functions will not be commutative. Commutativity is a special property, attained only by particular functions, and often in special circumstances. For example,
only when 
.
Considering functions as special cases of relations
(namely functional relations), one can analogously define composition of relations
, which gives the formula for
in terms of 
and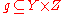 
.
Derivative
s of compositions involving differentiable functions can be found using the chain rule
. Higher derivatives of such functions are given by Faà di Bruno's formula
.
The structures given by composition are axiomatized and generalized in category theory
.
Then describes the oxygen concentration around the plane at time t.
then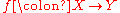
may compose with itself; this is sometimes denoted 
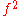. Thus:
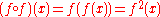
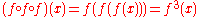
Repeated composition of a function with itself is called function iteration
.
The functional powers
for natural
follow immediately.
Note: If f takes its values in a ring
(in particular for real or complex-valued f ), there is a risk of confusion, as f n could also stand for the n-fold product of f, e.g. .
(For trigonometric functions, usually the latter is meant, at least for positive exponents. For example, in trigonometry, this superscript notation represents standard exponentiation
when used with trigonometric function
s:
.
However, for negative exponents (especially −1), it nevertheless usually refers to the inverse function, e.g., tan−1 = arctan (≠ 1/tan).
In some cases, an expression for f in can be derived from the rule for g given non-integer values of r. This is called fractional iteration. For instance, a half iterate
of a function f is a function g satisfying Another example would be that where f is the successor function, This idea can be generalized so that the iteration count becomes a continuous parameter; in this case, such a system is called a flow
.
Iterated functions and flows occur naturally in the study of fractals and dynamical systems.
of a monoid
, called transformation monoid or composition monoid. In general, composition monoids can have remarkably complicated structure. One particular notable example is the de Rham curve
. The set of all functions is called the full transformation semigroup on X.
If the functions are bijective, then the set of all possible combinations of these functions forms a transformation group; and one says that the group is generated by these functions.
The set of all bijective functions form a group with respect to the composition operator. This is the symmetric group
, also sometimes called the composition group.
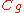is defined as that operator which maps functions to functions as
Composition operators are studied in the field of operator theory
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, function composition is the application of one function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f(x) instead of x. Intuitively, if z is a function g of y and y is a function f of x, then z is a function of x.
Thus one obtains a composite function : defined by for all x in X. The notation is read as "g circle f", or "g composed with f", "g after f", "g following f", or just "g of f".
The composition of functions is always associative. That is, if f, g, and h are three functions with suitably chosen domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
s and codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
s, then , where the parentheses serve to indicate that composition is to be performed first for the parenthesized functions. Since there is no distinction between the choices of placement of parentheses, they may be safely left off.
The functions g and f are said to commute with each other if . In general, composition of functions will not be commutative. Commutativity is a special property, attained only by particular functions, and often in special circumstances. For example,
only when .Considering functions as special cases of relations
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
(namely functional relations), one can analogously define composition of relations
Composition of relations
In mathematics, the composition of binary relations is a concept of forming a new relation from two given relations R and S, having as its most well-known special case the composition of functions.- Definition :...
, which gives the formula for
in terms of and 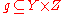.Derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s of compositions involving differentiable functions can be found using the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
. Higher derivatives of such functions are given by Faà di Bruno's formula
Faà di Bruno's formula
Faà di Bruno's formula is an identity in mathematics generalizing the chain rule to higher derivatives, named after , though he was not the first to state or prove the formula...
.
The structures given by composition are axiomatized and generalized in category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
.
Example
As an example, suppose that an airplane's elevation at time t is given by the function h(t) and that the oxygen concentration at elevation x is given by the function c(x).Then describes the oxygen concentration around the plane at time t.
Functional powers
IfSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
then
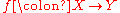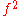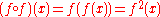
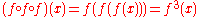
may compose with itself; this is sometimes denoted . Thus:Repeated composition of a function with itself is called function iteration
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
.
The functional powers
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
for natural
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
follow immediately.
- By convention,
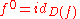
the identity map on the domain of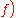 
. - If
admits an inverse functionInverse functionIn mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
, negative functional powers
are defined as the oppositeAdditive inverseIn mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
power of the inverse function,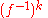
.
Note: If f takes its values in a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
(in particular for real or complex-valued f ), there is a risk of confusion, as f n could also stand for the n-fold product of f, e.g. .
(For trigonometric functions, usually the latter is meant, at least for positive exponents. For example, in trigonometry, this superscript notation represents standard exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
when used with trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s:
.
However, for negative exponents (especially −1), it nevertheless usually refers to the inverse function, e.g., tan−1 = arctan (≠ 1/tan).
In some cases, an expression for f in can be derived from the rule for g given non-integer values of r. This is called fractional iteration. For instance, a half iterate
Functional square root
In mathematics, a half iterate is a square root of a function with respect to the operation of function composition. In other words, a functional square root of a function g is a function f satisfying f = g for all x...
of a function f is a function g satisfying Another example would be that where f is the successor function, This idea can be generalized so that the iteration count becomes a continuous parameter; in this case, such a system is called a flow
Flow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
.
Iterated functions and flows occur naturally in the study of fractals and dynamical systems.
Composition monoids
Suppose one has two (or more) functions having the same domain and codomain. Then one can form long, potentially complicated chains of these functions composed together, such as . Such long chains have the algebraic structureAlgebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
of a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
, called transformation monoid or composition monoid. In general, composition monoids can have remarkably complicated structure. One particular notable example is the de Rham curve
De Rham curve
In mathematics, a de Rham curve is a certain type of fractal curve named in honor of Georges de Rham.The Cantor function, Césaro curve, Minkowski's question mark function, the Lévy C curve, the blancmange curve and the Koch curve are all special cases of the general de Rham...
. The set of all functions is called the full transformation semigroup on X.
If the functions are bijective, then the set of all possible combinations of these functions forms a transformation group; and one says that the group is generated by these functions.
The set of all bijective functions form a group with respect to the composition operator. This is the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
, also sometimes called the composition group.
Alternative notations
- Many mathematicians omit the composition symbol, writing gf for .
- In the mid-20th century, some mathematicians decided that writing to mean "first apply f, then apply g" was too confusing and decided to change notations. They write "xf" for "f(x)" and "(xf)g" for "g(f(x))". This can be more natural and seem simpler than writing functions on the left in some areas – in linear algebraLinear algebraLinear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, for instance, where x is a row vector and f and g denote matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
and the composition is by matrix multiplicationMatrix multiplicationIn mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
. This alternative notation is called postfix notation. The order is important because matrix multiplication is non-commutative. Successive transformations applying and composing to the right agrees with the left-to-right reading sequence.
- Mathematicians who use postfix notation may write "fg", meaning first do f then do g, in keeping with the order the symbols occur in postfix notation, thus making the notation "fg" ambiguous. Computer scientists may write "f;g" for this, thereby disambiguating the order of composition. To distinguish the left composition operator from a text semicolon, in the Z notationZ notationThe Z notation , named after Zermelo–Fraenkel set theory, is a formal specification language used for describing and modelling computing systems. It is targeted at the clear specification of computer programs and computer-based systems in general.-History:...
a fat semicolon ⨟ (U+2A1F) is used for left relation composition. Since all functions are binary relations, it is correct to use the fat semicolon for function composition as well (see the article on Composition of relationsComposition of relationsIn mathematics, the composition of binary relations is a concept of forming a new relation from two given relations R and S, having as its most well-known special case the composition of functions.- Definition :...
for further details on this notation).
Composition operator
Given a function g, the composition operator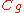 is defined as that operator which maps functions to functions asComposition operators are studied in the field of operator theory
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
.
See also
- Combinatory logicCombinatory logicCombinatory logic is a notation introduced by Moses Schönfinkel and Haskell Curry to eliminate the need for variables in mathematical logic. It has more recently been used in computer science as a theoretical model of computation and also as a basis for the design of functional programming...
- Composition of relationsComposition of relationsIn mathematics, the composition of binary relations is a concept of forming a new relation from two given relations R and S, having as its most well-known special case the composition of functions.- Definition :...
, the generalization to relationsRelation (mathematics)In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple... - Function composition (computer science)Function composition (computer science)In computer science, function composition is an act or mechanism to combine simple functions to build more complicated ones...
- Functional decompositionFunctional decompositionFunctional decomposition refers broadly to the process of resolving a functional relationship into its constituent parts in such a way that the original function can be reconstructed from those parts by function composition...
- Flow (mathematics)Flow (mathematics)In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
- Higher-order functionHigher-order functionIn mathematics and computer science, higher-order functions, functional forms, or functionals are functions which do at least one of the following:*take one or more functions as an input*output a function...
- Cobweb plotCobweb plotA cobweb plot, or Verhulst diagram is a visual tool used in the dynamical systems field of mathematics to investigate the qualitative behaviour of one dimensional iterated functions, such as the logistic map...
– a graphical technique for functional composition - Lambda calculusLambda calculusIn mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
- Functional square rootFunctional square rootIn mathematics, a half iterate is a square root of a function with respect to the operation of function composition. In other words, a functional square root of a function g is a function f satisfying f = g for all x...
External links
- "Composition of Functions" by Bruce Atwood, the Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
, 2007.