Biquaternion
Encyclopedia
In abstract algebra
, the biquaternions are the numbers
where w, x, y, and z are complex numbers and the elements of {1, i, j, k} multiply as in the quaternion group
. As there are three types of complex number, so there are three types of biquaternion:
The following article is about the ordinary biquaternions named by William Rowan Hamilton
in 1844 (see Proceedings of Royal Irish Academy 1844 & 1850 page 388 ). Some of the more prominent proponents of these biquaternions include Alexander Macfarlane
, Arthur W. Conway
, Ludwik Silberstein
, and Cornelius Lanczos
. As developed below, the unit quasi-sphere of the biquaternions provides a presentation of the Lorentz group
, which is the foundation of special relativity
.
The algebra of biquaternions can be considered as a tensor product
CH (taken over the reals) where C is the field
of complex numbers and H is the algebra of (real) quaternions. In other words, the biquaternions are just the complexification
of the (real) quaternions. Viewed as a complex algebra, the biquaternions are isomorphic to the algebra of 2×2 complex matrices M2(C).
In terms of Clifford algebra
they can be classified as Cℓ2(C) = Cℓ03(C). This is also isomorphic to the Pauli algebra Cℓ3,0(R), and the even part of the space-time algebra Cℓ01,3(R).
s, and let u, v, w, x be complex number
s, then
is a biquaternion.
To distinguish square roots of minus one in the biquaternions, Hamilton and Arthur W. Conway
used the convention of representing the square root of minus one in the scalar field C by h since there is an i in the quaternion group
. Then
Hamilton's primary exposition on biquaternions came in 1853 in his Lectures on Quaternions, now available in the Historical Mathematical Monographs of Cornell University. The two editions of Elements of Quaternions (1866 & 1899) reduced the biquaternion coverage in favor of the real quaternions. He introduced the terms bivector, biconjugate, bitensor, and biversor.
Considered with the operations of component-wise addition, and multiplication according to the quaternion group, this collection forms a 4-dimensional algebra
over the complex numbers. The algebra of biquaternions is associative, but not commutative. A biquaternion is either a unit
or a zero divisor
.
= 
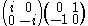where each of these three arrays has a square equal to the negative of the identity matrix
.
When this matrix product is interpreted as i j = k, then one obtains a subgroup
of the matrix group that is isomorphic
to the quaternion group
. Consequently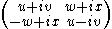
represents biquaternion q = = u 1 + v i + w j + x k.
Given any 2 × 2 complex matrix, there are complex values u, v, w, and x to put it in this form so that the matrix ring
is isomorphic to the biquaternion ring
.
{1, h, i, hi, j, hj, k, hk } forms a basis
so the algebra has eight real dimension
s.
Note the squares of the elements hi, hj, and hk are all plus one, for example,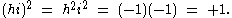
Then the subalgebra
given by
is ring isomorphic to the plane of split-complex number
s, which has an algebraic structure built upon the unit hyperbola
. The elements hj and hk also determine such subalgebras. Furthermore,
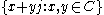is a subalgebra isomorphic to the tessarine
s.
A third subalgebra called coquaternion
s is generated by hj and hk. First note that
(hj)(hk) = (−1)i, and that the square of this element is −1. These elements generate the dihedral group
of the square. The linear subspace
with basis {1, i, hj, hk} thus is closed under multiplication, and forms the coquaternion algebra.
In the context of quantum mechanics
and spinor
algebra, the biquaternions hi, hj, and hk (or their negatives), viewed in the M(2,C) representation, are called Pauli matrices
.
where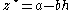
when 
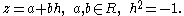
Note that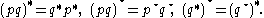
Clearly, if
then q is a zero divisor. Otherwise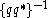 
is defined over the complex numbers. Further, 
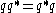is easily verified. This allows an inverse to be defined as follows:
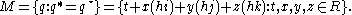
M is not a subalgebra since it is not closed under products
; for example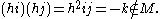
. Indeed, M cannot form an algebra if it is not even a magma
.
Proposition: If q is in M, then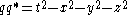
.
proof: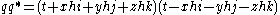
Definition: Let biquaternion g satisfy g g * = 1. Then the Lorentz transformation associated with g is given by
Proposition: If q is in M, then T(q) is also in M.
proof: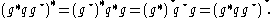
Proposition:
proof: Note first that g g * = 1 means that the sum of the squares of its four complex components is one. Then the sum of the squares of the complex conjugates of these components is also one. Therefore,
Now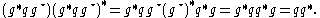
since the beginnings of mathematical physics
, there is an array of concepts that are illustrated or represented by biquaternion algebra. The transformation group
has two parts, 
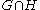and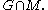 
The first part is characterized by 
; then the Lorentz transformation corresponding to g is given by 
since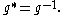 
Such a transformation is a rotation by quaternion multiplication
, and the collection of them is O(3)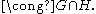
But this subgroup of G is not a normal subgroup
, so no quotient group
can be formed.
To view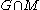
it is necessary to show some subalgebra structure in the biquaternions. Let r represent an element of the sphere of square roots of minus one in the real quaternion subalgebra H. Then (hr)2 = +1 and the plane of biquaternions given by 
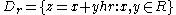is a commutative subalgebra isomorphic to the plane of split-complex number
s. Just as the ordinary complex plane has a unit circle,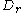
has a unit hyperbola
given by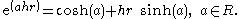
Just as the unit circle turns by multiplication through one of its elements, so the hyperbola turns because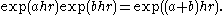
Hence these algebraic operators on the hyperbola are called hyperbolic versors. The unit circle in C and unit hyperbola in Dr are examples of one-parameter group
s. For every square root r of minus one in H, there is a one-parameter group in the biquaternions given by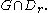
The space of biquaternions has a natural topology
through the Euclidean metric on 8-space. With respect to this topology, G is a topological group
. Moreover, it has analytic structure making it a six-parameter Lie group
. Consider the subspace of vector biquaternions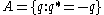
. Then the exponential map
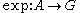takes the real vectors to 
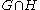and the h-vectors to 
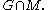When equipped with the commutator
, A forms the Lie algebra
of G. Thus this study of a six-dimensional space serves to introduce the general concepts of Lie theory
. When viewed in the matrix representation, G is called the special linear group
SL(2,C) in M(2,C).
Many of the concepts of special relativity
are illustrated through the biquaternion structures laid out. The subspace M corresponds to Minkowski space
, with the four coordinates giving the time and space locations of events in a resting frame of reference
. Any hyperbolic versor exp(ahr) corresponds to a velocity
in direction r of speed c tanh a where c is the velocity of light. The inertial frame of reference of this velocity can be made the resting frame by applying the Lorentz boost T given by g = exp(0.5ahr) since then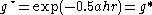
so that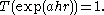 
Naturally the hyperboloid
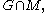which represents the range of velocities for sub-luminal motion, is of physical interest. There has been considerable work associating this "velocity space" with the hyperboloid model
of hyperbolic geometry
. In special relativity, the hyperbolic angle
parameter of a hyperbolic versor is called rapidity
. Thus we see the biquaternion group G provides a group representation
for the Lorentz group
.
After the introduction of spinor
theory, particularly in the hands of Wolfgang Pauli
and Élie Cartan
, the biquaternion representation of the Lorentz group was superseded. The new methods were founded on basis vectors
in the set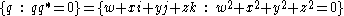
which is called the "complex light cone".
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the biquaternions are the numbers
where w, x, y, and z are complex numbers and the elements of {1, i, j, k} multiply as in the quaternion groupQuaternion group
In group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
. As there are three types of complex number, so there are three types of biquaternion:
- (Ordinary) biquaternions when the coefficients are (ordinary) complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s - split-biquaternions when w, x, y, and z are split-complex numberSplit-complex numberIn abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
s - Study biquaternionsEduard StudyEduard Study was a German mathematician known for work on invariant theory of ternary forms and for the study of spherical trigonometry. He is also known for contributions to space geometry, hypercomplex numbers, and criticism of early physical chemistry.Study was born in Coburg in the Duchy of...
or dual quaternionDual quaternionThe set of dual quaternions is an algebra that can be used to represent spatial rigid body displacements. A dual quaternion is an ordered pair of quaternions  = and therefore is constructed from eight real parameters. Because rigid body displacements are defined by six parameters, dual...
s when w, x, y, and z are dual numbers.
The following article is about the ordinary biquaternions named by William Rowan Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
in 1844 (see Proceedings of Royal Irish Academy 1844 & 1850 page 388 ). Some of the more prominent proponents of these biquaternions include Alexander Macfarlane
Alexander Macfarlane
Alexander Macfarlane was a Nova Scotia lawyer and political figure. He was a member of the Canadian Senate from 1870 to 1898. His surname also appears as McFarlane in some sources....
, Arthur W. Conway
Arthur W. Conway
Arthur William Conway FRS was President of University College Dublin between 1940 and 1947.Born in Wexford, he received his early education in St Peter’s College, Wexford and proceeded to enter old University College, Dublin in 1892. He received his BA Degree from the Royal University of Ireland...
, Ludwik Silberstein
Ludwik Silberstein
Ludwik Silberstein was a Polish-American physicist who helped make special relativity and general relativity staples of university coursework...
, and Cornelius Lanczos
Cornelius Lanczos
Cornelius Lanczos Löwy Kornél was a Hungarian-Jewish mathematician and physicist, who was born on February 2, 1893, and died on June 25, 1974....
. As developed below, the unit quasi-sphere of the biquaternions provides a presentation of the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
, which is the foundation of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
.
The algebra of biquaternions can be considered as a tensor product
Tensor product of algebras
In mathematics, the tensor product of two R-algebras is also an R-algebra. This gives us a tensor product of algebras. The special case R = Z gives us a tensor product of rings, since rings may be regarded as Z-algebras....
CH (taken over the reals) where C is the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of complex numbers and H is the algebra of (real) quaternions. In other words, the biquaternions are just the complexification
Complexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
of the (real) quaternions. Viewed as a complex algebra, the biquaternions are isomorphic to the algebra of 2×2 complex matrices M2(C).
In terms of Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
they can be classified as Cℓ2(C) = Cℓ03(C). This is also isomorphic to the Pauli algebra Cℓ3,0(R), and the even part of the space-time algebra Cℓ01,3(R).
Definition
Let {1, i, j, k} be the basis for the (real) quaternionQuaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s, and let u, v, w, x be complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, then
- q = u 1 + v i + w j + x k
is a biquaternion.
To distinguish square roots of minus one in the biquaternions, Hamilton and Arthur W. Conway
Arthur W. Conway
Arthur William Conway FRS was President of University College Dublin between 1940 and 1947.Born in Wexford, he received his early education in St Peter’s College, Wexford and proceeded to enter old University College, Dublin in 1892. He received his BA Degree from the Royal University of Ireland...
used the convention of representing the square root of minus one in the scalar field C by h since there is an i in the quaternion group
Quaternion group
In group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
. Then
- hi = ih, hj = jh, and hk = kh since h is a scalar.
Hamilton's primary exposition on biquaternions came in 1853 in his Lectures on Quaternions, now available in the Historical Mathematical Monographs of Cornell University. The two editions of Elements of Quaternions (1866 & 1899) reduced the biquaternion coverage in favor of the real quaternions. He introduced the terms bivector, biconjugate, bitensor, and biversor.
Considered with the operations of component-wise addition, and multiplication according to the quaternion group, this collection forms a 4-dimensional algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
over the complex numbers. The algebra of biquaternions is associative, but not commutative. A biquaternion is either a unit
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
or a zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
.
Linear representation
Note the matrix product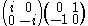 = where each of these three arrays has a square equal to the negative of the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
.
When this matrix product is interpreted as i j = k, then one obtains a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of the matrix group that is isomorphic
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to the quaternion group
Quaternion group
In group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
. Consequently
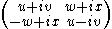represents biquaternion q = = u 1 + v i + w j + x k.Given any 2 × 2 complex matrix, there are complex values u, v, w, and x to put it in this form so that the matrix ring
Matrix ring
In abstract algebra, a matrix ring is any collection of matrices forming a ring under matrix addition and matrix multiplication. The set of n×n matrices with entries from another ring is a matrix ring, as well as some subsets of infinite matrices which form infinite matrix rings...
is isomorphic to the biquaternion ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
.
Subalgebras
Considering the biquaternion algebra over the scalar field of real numbers R, the set{1, h, i, hi, j, hj, k, hk } forms a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
so the algebra has eight real dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s.
Note the squares of the elements hi, hj, and hk are all plus one, for example,
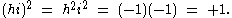
Then the subalgebra
Subalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
given by
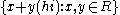is ring isomorphic to the plane of split-complex numberSplit-complex number
In abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
s, which has an algebraic structure built upon the unit hyperbola
Unit hyperbola
In geometry, the unit hyperbola is the set of points in the Cartesian plane that satisfies x^2 - y^2 = 1 . In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial lengthWhereas the unit circle surrounds its center, the unit hyperbola requires the...
. The elements hj and hk also determine such subalgebras. Furthermore,
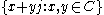is a subalgebra isomorphic to the tessarineTessarine
In mathematics, a tessarine is a hypercomplex number of the formt = w + x i + y j + z k, \quad w, x, y, z \in Rwhere i j = j i = k, \quad i^2 = -1, \quad j^2 = +1 .The tessarines are best known for their subalgebra of real tessarines t = w + y j \ ,...
s.
A third subalgebra called coquaternion
Coquaternion
In abstract algebra, the split-quaternions or coquaternions are elements of a 4-dimensional associative algebra introduced by James Cockle in 1849 under the latter name. Like the quaternions introduced by Hamilton in 1843, they form a four dimensional real vector space equipped with a...
s is generated by hj and hk. First note that
(hj)(hk) = (−1)i, and that the square of this element is −1. These elements generate the dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
of the square. The linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
with basis {1, i, hj, hk} thus is closed under multiplication, and forms the coquaternion algebra.
In the context of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
and spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
algebra, the biquaternions hi, hj, and hk (or their negatives), viewed in the M(2,C) representation, are called Pauli matrices
Pauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
.
Algebraic properties
The biquaternions have two conjugations:- the quaternion conjugation
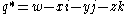, and - the complex conjugation of quaternion coefficients
where
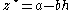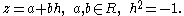
when Note that
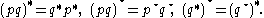
Clearly, if
then q is a zero divisor. Otherwise 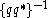is defined over the complex numbers. Further, 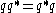is easily verified. This allows an inverse to be defined as follows:
-
, iff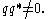 
Relation to Lorentz Transformations
Consider now the linear subspace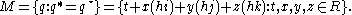M is not a subalgebra since it is not closed under products
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
; for example
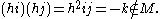. Indeed, M cannot form an algebra if it is not even a magmaMagma (algebra)
In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
.
Proposition: If q is in M, then
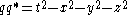.proof:
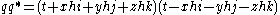
Definition: Let biquaternion g satisfy g g * = 1. Then the Lorentz transformation associated with g is given by
Proposition: If q is in M, then T(q) is also in M.
proof:
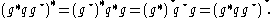
Proposition:
proof: Note first that g g * = 1 means that the sum of the squares of its four complex components is one. Then the sum of the squares of the complex conjugates of these components is also one. Therefore,
Now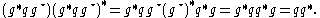Associated terminology
As the biquaternions have been a fixture of linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
since the beginnings of mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, there is an array of concepts that are illustrated or represented by biquaternion algebra. The transformation group
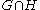has two parts, and 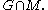The first part is characterized by ; then the Lorentz transformation corresponding to g is given by since 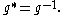Such a transformation is a rotation by quaternion multiplicationQuaternions and spatial rotation
Unit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
, and the collection of them is O(3)
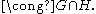But this subgroup of G is not a normal subgroupNormal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
, so no quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
can be formed.
To view
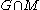it is necessary to show some subalgebra structure in the biquaternions. Let r represent an element of the sphere of square roots of minus one in the real quaternion subalgebra H. Then (hr)2 = +1 and the plane of biquaternions given by 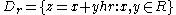is a commutative subalgebra isomorphic to the plane of split-complex numberSplit-complex number
In abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
s. Just as the ordinary complex plane has a unit circle,
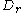has a unit hyperbolaUnit hyperbola
In geometry, the unit hyperbola is the set of points in the Cartesian plane that satisfies x^2 - y^2 = 1 . In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial lengthWhereas the unit circle surrounds its center, the unit hyperbola requires the...
given by
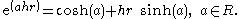
Just as the unit circle turns by multiplication through one of its elements, so the hyperbola turns because
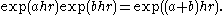Hence these algebraic operators on the hyperbola are called hyperbolic versors. The unit circle in C and unit hyperbola in Dr are examples of one-parameter groupOne-parameter group
In mathematics, a one-parameter group or one-parameter subgroup usually means a continuous group homomorphismfrom the real line R to some other topological group G...
s. For every square root r of minus one in H, there is a one-parameter group in the biquaternions given by
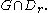
The space of biquaternions has a natural topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
through the Euclidean metric on 8-space. With respect to this topology, G is a topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
. Moreover, it has analytic structure making it a six-parameter Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
. Consider the subspace of vector biquaternions
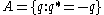. Then the exponential mapExponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
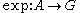takes the real vectors to 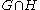and the h-vectors to 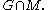When equipped with the commutatorCommutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
, A forms the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of G. Thus this study of a six-dimensional space serves to introduce the general concepts of Lie theory
Lie theory
Lie theory is an area of mathematics, developed initially by Sophus Lie.Early expressions of Lie theory are found in books composed by Lie with Friedrich Engel and Georg Scheffers from 1888 to 1896....
. When viewed in the matrix representation, G is called the special linear group
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
SL(2,C) in M(2,C).
Many of the concepts of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
are illustrated through the biquaternion structures laid out. The subspace M corresponds to Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
, with the four coordinates giving the time and space locations of events in a resting frame of reference
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
. Any hyperbolic versor exp(ahr) corresponds to a velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
in direction r of speed c tanh a where c is the velocity of light. The inertial frame of reference of this velocity can be made the resting frame by applying the Lorentz boost T given by g = exp(0.5ahr) since then
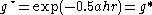so that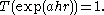 Naturally the hyperboloid
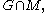which represents the range of velocities for sub-luminal motion, is of physical interest. There has been considerable work associating this "velocity space" with the hyperboloid modelHyperboloid model
In geometry, the hyperboloid model, also known as the Minkowski model or the Lorentz model , is a model of n-dimensional hyperbolic geometry in which points are represented by the points on the forward sheet S+ of a two-sheeted hyperboloid in -dimensional Minkowski space and m-planes are...
of hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
. In special relativity, the hyperbolic angle
Hyperbolic angle
In mathematics, a hyperbolic angle is a geometric figure that divides a hyperbola. The science of hyperbolic angle parallels the relation of an ordinary angle to a circle...
parameter of a hyperbolic versor is called rapidity
Rapidity
In relativity, rapidity is an alternative to speed as a framework for measuring motion. On parallel velocities rapidities are simply additive, unlike speeds at relativistic velocities. For low speeds, rapidity and speed are proportional, but for high speeds, rapidity takes a larger value. The...
. Thus we see the biquaternion group G provides a group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
for the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
.
After the introduction of spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
theory, particularly in the hands of Wolfgang Pauli
Wolfgang Pauli
Wolfgang Ernst Pauli was an Austrian theoretical physicist and one of the pioneers of quantum physics. In 1945, after being nominated by Albert Einstein, he received the Nobel Prize in Physics for his "decisive contribution through his discovery of a new law of Nature, the exclusion principle or...
and Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
, the biquaternion representation of the Lorentz group was superseded. The new methods were founded on basis vectors
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
in the set
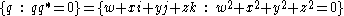
which is called the "complex light cone".
See also
- Conic octonions (isomorphism)
- MacFarlane's use
- Quotient ring
- Hypercomplex numberHypercomplex numberIn mathematics, a hypercomplex number is a traditional term for an element of an algebra over a field where the field is the real numbers or the complex numbers. In the nineteenth century number systems called quaternions, tessarines, coquaternions, biquaternions, and octonions became established...