.gif)
Domain (mathematics)
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the domain of definition or simply the domain of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
is the set of "input" or argument
Argument of a function
In mathematics, an argument of a function is a specific input in the function, also known as an independent variable. When it is clear from the context which argument is meant, the argument is often denoted by arg....
values for which the function is defined. That is, the function provides an "output" or value
Value (mathematics)
In mathematics, value commonly refers to the 'output' of a function. In the most basic case, that of unary, single-valued functions, there is one input and one output .The function f of the example is real-valued, since each and every possible function value is real...
for each member of the domain.
For instance, the domain of cosine is the set of all real numbers, while the domain of the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
consists only of numbers greater than or equal to 0 (ignoring complex numbers in both cases). For a function whose domain is a subset of the real numbers, when the function is represented in an xy Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
, the domain is represented on the x-axis.
Formal definition
Given a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
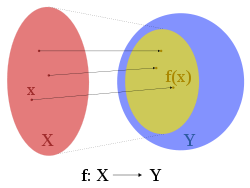
f:X→Y, the set X is the domain of f; the set Y is the codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
of f. In the expression f(x), x is the argument and f(x) is the value. One can think of an argument as an input to the function, and the value as the output.
The image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
(sometimes called the range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
) of f is the set of all values assumed by f for all possible x; this is the set
 . The image of f can be the same set as the codomain or it can be a proper subset of it. It is in general smaller than the codomain; it is the whole codomain if and only if f is a surjective function
. The image of f can be the same set as the codomain or it can be a proper subset of it. It is in general smaller than the codomain; it is the whole codomain if and only if f is a surjective functionSurjective function
In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
.
A well-defined function must carry every element of its domain to an element of its codomain. For example, the function f defined by
- f(x) = 1/x
has no value for f(0).
Thus, the set of all real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s,
 , cannot be its domain.
, cannot be its domain.In cases like this, the function is either defined on
 or the "gap is plugged" by explicitly defining f(0).
or the "gap is plugged" by explicitly defining f(0).If we extend the definition of f to
- f(x) = 1/x, for x ≠ 0,
- f(0) = 0,
then f is defined for all real numbers, and its domain is
 .
.Any function can be restricted to a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of its domain.
The restriction of g : A → B to S, where S ⊆ A, is written g |S : S → B.
Natural domain
The natural domain of a formula is the set of values for which it is defined, typically within the reals but sometimes among the integers or complex numbers. For instance the natural domain of square root is the non-negative reals when considered as a real number function. When considering a natural domain the set of possible values of the function is typically called its range.Domain of a partial function
There are two distinct meanings in current mathematical usage for the notion of the domain of a partial functionPartial function
In mathematics, a partial function from X to Y is a function ƒ: X' → Y, where X' is a subset of X. It generalizes the concept of a function by not forcing f to map every element of X to an element of Y . If X' = X, then ƒ is called a total function and is equivalent to a function...
from X to Y, i.e. a function from a subset X
Recursion theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
, use the term "domain of f" for the set X
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, consider the domain to be X, irrespective of whether f(x) exists for every x in X.
Category theory
In category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
one deals with morphisms instead of functions. Morphisms are arrows from one object to another. The domain of any morphism is the object from which an arrow starts. In this context, many set theoretic ideas about domains must be abandoned or at least formulated more abstractly. For example, the notion of restricting a morphism to a subset of its domain must be modified. See subobject
Subobject
In category theory, a branch of mathematics, a subobject is, roughly speaking, an object which sits inside another object in the same category. The notion is a generalization of the older concepts of subset from set theory and subgroup from group theory...
for more.
Real and complex analysis
In realCalculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
and complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a domain is an open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
subset of a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
vector space.
In partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s, a domain is an open connected subset of the euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn, where the problem is posed, i.e., where the unknown function(s) are defined.
More examples
- Function
 is defined for all
is defined for all  .
. - Function
 , where
, where  is the set of all complex numbers, is defined for all x.
is the set of all complex numbers, is defined for all x. - Function
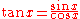 is defined for all
is defined for all 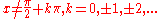
See also
- Range (mathematics)Range (mathematics)In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
- CodomainCodomainIn mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
- Surjective functionSurjective functionIn mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
- Injective functionInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
- BijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
- Domain decomposition
- Lipschitz domainLipschitz domainIn mathematics, a Lipschitz domain is a domain in Euclidean space whose boundary is "sufficiently regular" in the sense that it can be thought of as locally being the graph of a Lipschitz continuous function...
- Effective domain

