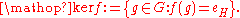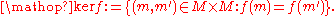Kernel (algebra)
Encyclopedia
In the various branches of mathematics
that fall under the heading of abstract algebra
, the kernel of a homomorphism
measures the degree to which the homomorphism fails to be injective
. An important special case is the kernel of a matrix, also called the null space.
The definition of kernel takes various forms in various contexts. But in all of them, the kernel of a homomorphism is trivial (in a sense relevant to that context) if and only if the homomorphism is injective
. The fundamental theorem on homomorphisms
(or first isomorphism theorem) is a theorem, again taking various forms, that applies to the quotient algebra
defined by the kernel.
In this article, we first survey kernels for some important types of algebraic structure
s; then we give general definitions from universal algebra
for generic algebraic structures.
s and let T be a linear transformation
from V to W. If 0W is the zero vector of W, then the kernel of T is the preimage of the singleton set {0W }; that is, the subset
of V consisting of all those elements of V that are mapped by T to the element 0W. The kernel is usually denoted as "ker T ", or some variation thereof:
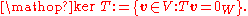
Since a linear transformation preserves zero vectors, the zero vector 0V of V must belong to the kernel. The transformation T is injective if and only if its kernel is only the singleton set {0V }.
It turns out that ker T is always a linear subspace
of V. Thus, it makes sense to speak of the quotient space
V /(ker T ). The first isomorphism theorem for vector spaces states that this quotient space is naturally isomorphic to the image of T (which is a subspace of W). As a consequence, the dimension of V equals the dimension of the kernel plus the dimension of the image.
If V and W are finite-dimensional and bases
have been chosen, then T can be described by a matrix
M, and the kernel can be computed by solving the homogeneous system of linear equations M v = 0. In this representation, the kernel corresponds to the null space of M. The dimension of the null space, called the nullity of M, is given by the number of columns of M minus the rank of M, as a consequence of the rank-nullity theorem
.
Solving homogeneous differential equation
s often amounts to computing the kernel of certain differential operator
s.
For instance, in order to find all twice-differentiable function
s f from the real line
to itself such that
let V be the space of all twice differentiable functions, let W be the space of all functions, and define a linear operator T from V to W by (x) + 3f '(x) - f (x)
for f in V and x an arbitrary real number
.
Then all solutions to the differential equation are in ker T.
One can define kernels for homomorphism
s between module
s over a ring
in an analogous manner.
This includes kernels for homomorphisms between abelian group
s as a special case.
This example captures the essence of kernels in general abelian categories; see Kernel (category theory)
.
s and let f be a group homomorphism
from G to H.
If eH is the identity element
of H, then the kernel of f is the preimage of the singleton set {eH }; that is, the subset of G consisting of all those elements of G that are mapped by f to the element eH .
The kernel is usually denoted "ker f " (or a variation).
In symbols:
Since a group homomorphism preserves identity elements, the identity element eG of G must belong to the kernel.
The homomorphism f is injective if and only if its kernel is only the singleton set {eG}.
It turns out that ker f is not only a subgroup
of G but in fact a normal subgroup
.
Thus, it makes sense to speak of the quotient group
G /(ker f ).
The first isomorphism theorem for groups states that this quotient group is naturally isomorphic to the image of f (which is a subgroup of H).
In the special case of abelian group
s, this works in exactly the same way as in the previous section.
s (assumed unital) and let f be a ring homomorphism
from R to S.
If 0S is the zero element
of S, then the kernel of f is the preimage of the singleton set {0S}; that is, the subset of R consisting of all those elements of R that are mapped by f to the element 0S.
The kernel is usually denoted "ker f" (or a variation).
In symbols:
Since a ring homomorphism preserves zero elements, the zero element 0R of R must belong to the kernel.
The homomorphism f is injective if and only if its kernel is only the singleton set {0R}.
It turns out that, although ker f is generally not a subring
of R since it may not contain the multiplicative identity, it is nevertheless a two-sided ideal
of R.
Thus, it makes sense to speak of the quotient ring
R/(ker f).
The first isomorphism theorem for rings states that this quotient ring is naturally isomorphic to the image of f (which is a subring of S).
To some extent, this can be thought of as a special case of the situation for modules, since these are all bimodule
s over a ring R:
However, the isomorphism theorem gives a stronger result, because ring isomorphisms preserve multiplication while module isomorphisms (even between rings) in general do not.
This example captures the essence of kernels in general Mal'cev algebras.
Then the kernel of f is the subset of the direct product
M × M consisting of all those ordered pair
s of elements of M whose components are both mapped by f to the same element in N.
The kernel is usually denoted "ker f" (or a variation).
In symbols:
Since f is a function
, the elements of the form (m,m) must belong to the kernel.
The homomorphism f is injective if and only if its kernel is only the diagonal set {(m,m) : m in M}.
It turns out that ker f is an equivalence relation
on M, and in fact a congruence relation
.
Thus, it makes sense to speak of the quotient monoid M/(ker f).
The first isomorphism theorem for monoids states that this quotient monoid is naturally isomorphic to the image of f (which is a submonoid of N).
This is very different in flavour from the above examples.
In particular, the preimage of the identity element of N is not enough to determine the kernel of f.
This is because monoids are not Mal'cev algebras.
s of a given type and let f be a homomorphism
of that type from A to B.
Then the kernel of f is the subset of the direct product
A × A consisting of all those ordered pair
s of elements of A whose components are both mapped by f to the same element in B.
The kernel is usually denoted "ker f" (or a variation).
In symbols:
Since f is a function
, the elements of the form (a,a) must belong to the kernel.
The homomorphism f is injective if and only if its kernel is only the diagonal set {(a,a) : a in A}.
It turns out that ker f is an equivalence relation
on A, and in fact a congruence relation
.
Thus, it makes sense to speak of the quotient algebra
A/(ker f).
The first isomorphism theorem in general universal algebra states that this quotient algebra is naturally isomorphic to the image of f (which is a subalgebra
of B).
Note that the definition of kernel here (as in the monoid example) doesn't depend on the algebraic structure; it is a purely set-theoretic concept.
For more on this general concept, outside of abstract algebra, see kernel of a function
.
s, the identity element
in the case of group
s, and the zero element
in the case of ring
s or module
s). The characteristic feature of a Mal'cev algebra is that we can recover the entire equivalence relation ker f from the equivalence class of the neutral element.
To be specific, let A and B be Mal'cev algebraic structures of a given type and let f be a homomorphism of that type from A to B. If eB is the neutral element of B, then the kernel of f is the preimage of the singleton set {eB}; that is, the subset
of A consisting of all those elements of A that are mapped by f to the element eB.
The kernel is usually denoted "ker f" (or a variation). In symbols:
Since a Mal'cev algebra homomorphism preserves neutral elements, the identity element eA of A must belong to the kernel. The homomorphism f is injective if and only if its kernel is only the singleton set {eA}.
The notion of ideal generalises to any Mal'cev algebra (as linear subspace
in the case of vector spaces, normal subgroup
in the case of groups, two-sided ring ideal in the case of rings, and submodule in the case of modules).
It turns out that although ker f may not be a subalgebra
of A, it is nevertheless an ideal.
Then it makes sense to speak of the quotient algebra
G/(ker f).
The first isomorphism theorem for Mal'cev algebras states that this quotient algebra is naturally isomorphic to the image of f (which is a subalgebra of B).
The connection between this and the congruence relation is for more general types of algebras is as follows.
First, the kernel-as-an-ideal is the equivalence class of the neutral element eA under the kernel-as-a-congruence. For the converse direction, we need the notion of quotient
in the Mal'cev algebra (which is division
on either side for groups and subtraction
for vector spaces, modules, and rings).
Using this, elements a and a of A are equivalent under the kernel-as-a-congruence if and only if their quotient a/a is an element of the kernel-as-an-ideal.
For example, one may consider topological group
s or topological vector space
s, with are equipped with a topology.
In this case, we would expect the homomorphism f to preserve this additional structure; in the topological examples, we would want f to be a continuous map.
The process may run into a snag with the quotient algebras, which may not be well-behaved.
In the topological examples, we can avoid problems by requiring that topological algebraic structures be Hausdorff
(as is usually done); then the kernel (however it is constructed) will be a closed set
and the quotient space will work fine (and also be Hausdorff).
is a generalisation of the kernels of abelian algebras; see Kernel (category theory)
.
The categorical generalisation of the kernel as a congruence relation is the kernel pair.
(There is also the notion of difference kernel, or binary equaliser
.)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
that fall under the heading of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the kernel of a homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
measures the degree to which the homomorphism fails to be injective
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
. An important special case is the kernel of a matrix, also called the null space.
The definition of kernel takes various forms in various contexts. But in all of them, the kernel of a homomorphism is trivial (in a sense relevant to that context) if and only if the homomorphism is injective
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
. The fundamental theorem on homomorphisms
Fundamental theorem on homomorphisms
In abstract algebra, the fundamental theorem on homomorphisms, also known as the fundamental homomorphism theorem, relates the structure of two objects between which a homomorphism is given, and of the kernel and image of the homomorphism....
(or first isomorphism theorem) is a theorem, again taking various forms, that applies to the quotient algebra
Quotient algebra
In mathematics, a quotient algebra, , also called a factor algebra is obtained by partitioning the elements of an algebra in equivalence classes given by a congruence, that is an equivalence relation that is additionally compatible with all the operations of the algebra, in the formal sense...
defined by the kernel.
In this article, we first survey kernels for some important types of algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s; then we give general definitions from universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
for generic algebraic structures.
Linear operators
Let V and W be vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s and let T be a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
from V to W. If 0W is the zero vector of W, then the kernel of T is the preimage of the singleton set {0W }; that is, the subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of V consisting of all those elements of V that are mapped by T to the element 0W. The kernel is usually denoted as "ker T ", or some variation thereof:
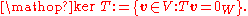
Since a linear transformation preserves zero vectors, the zero vector 0V of V must belong to the kernel. The transformation T is injective if and only if its kernel is only the singleton set {0V }.
It turns out that ker T is always a linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of V. Thus, it makes sense to speak of the quotient space
Quotient space (linear algebra)
In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
V /(ker T ). The first isomorphism theorem for vector spaces states that this quotient space is naturally isomorphic to the image of T (which is a subspace of W). As a consequence, the dimension of V equals the dimension of the kernel plus the dimension of the image.
If V and W are finite-dimensional and bases
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
have been chosen, then T can be described by a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
M, and the kernel can be computed by solving the homogeneous system of linear equations M v = 0. In this representation, the kernel corresponds to the null space of M. The dimension of the null space, called the nullity of M, is given by the number of columns of M minus the rank of M, as a consequence of the rank-nullity theorem
Rank-nullity theorem
In mathematics, the rank–nullity theorem of linear algebra, in its simplest form, states that the rank and the nullity of a matrix add up to the number of columns of the matrix. Specifically, if A is an m-by-n matrix over some field, thenThis applies to linear maps as well...
.
Solving homogeneous differential equation
Homogeneous differential equation
The term homogeneous differential equation has several distinct meanings.One meaning is that a first-order ordinary differential equation is homogeneous if it has the formwhere F is a homogeneous function of degree zero; that is to say, that F = F.In a related, but distinct, usage, the term linear...
s often amounts to computing the kernel of certain differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s.
For instance, in order to find all twice-differentiable function
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
s f from the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
to itself such that
- x f
let V be the space of all twice differentiable functions, let W be the space of all functions, and define a linear operator T from V to W by
- (
for f in V and x an arbitrary real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
.
Then all solutions to the differential equation are in ker T.
One can define kernels for homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s between module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
s over a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
in an analogous manner.
This includes kernels for homomorphisms between abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s as a special case.
This example captures the essence of kernels in general abelian categories; see Kernel (category theory)
Kernel (category theory)
In category theory and its applications to other branches of mathematics, kernels are a generalization of the kernels of group homomorphisms, the kernels of module homomorphisms and certain other kernels from algebra...
.
Group homomorphisms
Let G and H be groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s and let f be a group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
from G to H.
If eH is the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
of H, then the kernel of f is the preimage of the singleton set {eH }; that is, the subset of G consisting of all those elements of G that are mapped by f to the element eH .
The kernel is usually denoted "ker f " (or a variation).
In symbols:
Since a group homomorphism preserves identity elements, the identity element eG of G must belong to the kernel.
The homomorphism f is injective if and only if its kernel is only the singleton set {eG}.
It turns out that ker f is not only a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of G but in fact a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
.
Thus, it makes sense to speak of the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
G /(ker f ).
The first isomorphism theorem for groups states that this quotient group is naturally isomorphic to the image of f (which is a subgroup of H).
In the special case of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s, this works in exactly the same way as in the previous section.
Ring homomorphisms
Let R and S be ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
s (assumed unital) and let f be a ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
from R to S.
If 0S is the zero element
Zero element
In mathematics, a zero element is one of several generalizations of the number zero to other algebraic structures. These alternate meanings may or may not reduce to the same thing, depending on the context.-Additive identities:...
of S, then the kernel of f is the preimage of the singleton set {0S}; that is, the subset of R consisting of all those elements of R that are mapped by f to the element 0S.
The kernel is usually denoted "ker f" (or a variation).
In symbols:
Since a ring homomorphism preserves zero elements, the zero element 0R of R must belong to the kernel.
The homomorphism f is injective if and only if its kernel is only the singleton set {0R}.
It turns out that, although ker f is generally not a subring
Subring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
of R since it may not contain the multiplicative identity, it is nevertheless a two-sided ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of R.
Thus, it makes sense to speak of the quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
R/(ker f).
The first isomorphism theorem for rings states that this quotient ring is naturally isomorphic to the image of f (which is a subring of S).
To some extent, this can be thought of as a special case of the situation for modules, since these are all bimodule
Bimodule
In abstract algebra a bimodule is an abelian group that is both a left and a right module, such that the left and right multiplications are compatible...
s over a ring R:
- R itself;
- any two-sided ideal of R (such as ker f);
- any quotient ring of R (such as R/(ker f)); and
- the codomainCodomainIn mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
of any ring homomorphism whose domain is R (such as S, the codomain of f).
However, the isomorphism theorem gives a stronger result, because ring isomorphisms preserve multiplication while module isomorphisms (even between rings) in general do not.
This example captures the essence of kernels in general Mal'cev algebras.
Monoid homomorphisms
Let M and N be monoids and let f be a monoid homomorphism from M to N.Then the kernel of f is the subset of the direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
M × M consisting of all those ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
s of elements of M whose components are both mapped by f to the same element in N.
The kernel is usually denoted "ker f" (or a variation).
In symbols:
Since f is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, the elements of the form (m,m) must belong to the kernel.
The homomorphism f is injective if and only if its kernel is only the diagonal set {(m,m) : m in M}.
It turns out that ker f is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on M, and in fact a congruence relation
Congruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
.
Thus, it makes sense to speak of the quotient monoid M/(ker f).
The first isomorphism theorem for monoids states that this quotient monoid is naturally isomorphic to the image of f (which is a submonoid of N).
This is very different in flavour from the above examples.
In particular, the preimage of the identity element of N is not enough to determine the kernel of f.
This is because monoids are not Mal'cev algebras.
General case
Let A and B be algebraic structureAlgebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s of a given type and let f be a homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
of that type from A to B.
Then the kernel of f is the subset of the direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
A × A consisting of all those ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
s of elements of A whose components are both mapped by f to the same element in B.
The kernel is usually denoted "ker f" (or a variation).
In symbols:
Since f is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, the elements of the form (a,a) must belong to the kernel.
The homomorphism f is injective if and only if its kernel is only the diagonal set {(a,a) : a in A}.
It turns out that ker f is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on A, and in fact a congruence relation
Congruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
.
Thus, it makes sense to speak of the quotient algebra
Quotient algebra
In mathematics, a quotient algebra, , also called a factor algebra is obtained by partitioning the elements of an algebra in equivalence classes given by a congruence, that is an equivalence relation that is additionally compatible with all the operations of the algebra, in the formal sense...
A/(ker f).
The first isomorphism theorem in general universal algebra states that this quotient algebra is naturally isomorphic to the image of f (which is a subalgebra
Subalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
of B).
Note that the definition of kernel here (as in the monoid example) doesn't depend on the algebraic structure; it is a purely set-theoretic concept.
For more on this general concept, outside of abstract algebra, see kernel of a function
Kernel of a function
In set theory, the kernel of a function f may be taken to be either*the equivalence relation on the function's domain that roughly expresses the idea of "equivalent as far as the function f can tell", or*the corresponding partition of the domain....
.
Mal'cev algebras
In the case of Mal'cev algebras, this construction can be simplified. Every Mal'cev algebra has a special neutral element (the zero vector in the case of vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s, the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
in the case of group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s, and the zero element
Zero element
In mathematics, a zero element is one of several generalizations of the number zero to other algebraic structures. These alternate meanings may or may not reduce to the same thing, depending on the context.-Additive identities:...
in the case of ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
s or module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
s). The characteristic feature of a Mal'cev algebra is that we can recover the entire equivalence relation ker f from the equivalence class of the neutral element.
To be specific, let A and B be Mal'cev algebraic structures of a given type and let f be a homomorphism of that type from A to B. If eB is the neutral element of B, then the kernel of f is the preimage of the singleton set {eB}; that is, the subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of A consisting of all those elements of A that are mapped by f to the element eB.
The kernel is usually denoted "ker f" (or a variation). In symbols:
Since a Mal'cev algebra homomorphism preserves neutral elements, the identity element eA of A must belong to the kernel. The homomorphism f is injective if and only if its kernel is only the singleton set {eA}.
The notion of ideal generalises to any Mal'cev algebra (as linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
in the case of vector spaces, normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
in the case of groups, two-sided ring ideal in the case of rings, and submodule in the case of modules).
It turns out that although ker f may not be a subalgebra
Subalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
of A, it is nevertheless an ideal.
Then it makes sense to speak of the quotient algebra
Quotient algebra
In mathematics, a quotient algebra, , also called a factor algebra is obtained by partitioning the elements of an algebra in equivalence classes given by a congruence, that is an equivalence relation that is additionally compatible with all the operations of the algebra, in the formal sense...
G/(ker f).
The first isomorphism theorem for Mal'cev algebras states that this quotient algebra is naturally isomorphic to the image of f (which is a subalgebra of B).
The connection between this and the congruence relation is for more general types of algebras is as follows.
First, the kernel-as-an-ideal is the equivalence class of the neutral element eA under the kernel-as-a-congruence. For the converse direction, we need the notion of quotient
Quotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
in the Mal'cev algebra (which is division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
on either side for groups and subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
for vector spaces, modules, and rings).
Using this, elements a and a of A are equivalent under the kernel-as-a-congruence if and only if their quotient a/a is an element of the kernel-as-an-ideal.
Algebras with nonalgebraic structure
Sometimes algebras are equipped with a nonalgebraic structure in addition to their algebraic operations.For example, one may consider topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
s or topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s, with are equipped with a topology.
In this case, we would expect the homomorphism f to preserve this additional structure; in the topological examples, we would want f to be a continuous map.
The process may run into a snag with the quotient algebras, which may not be well-behaved.
In the topological examples, we can avoid problems by requiring that topological algebraic structures be Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
(as is usually done); then the kernel (however it is constructed) will be a closed set
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
and the quotient space will work fine (and also be Hausdorff).
Kernels in category theory
The notion of kernel in category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
is a generalisation of the kernels of abelian algebras; see Kernel (category theory)
Kernel (category theory)
In category theory and its applications to other branches of mathematics, kernels are a generalization of the kernels of group homomorphisms, the kernels of module homomorphisms and certain other kernels from algebra...
.
The categorical generalisation of the kernel as a congruence relation is the kernel pair.
(There is also the notion of difference kernel, or binary equaliser
Equaliser
In mathematics, an equaliser, or equalizer, is a set of arguments where two or more functions have equal values.An equaliser is the solution set of an equation.In certain contexts, a difference kernel is the equaliser of exactly two functions....
.)