Modular arithmetic
Encyclopedia
In mathematics
, modular arithmetic (sometimes called clock arithmetic) is a system of arithmetic
for integer
s, where numbers "wrap around" after they reach a certain value—the modulus.
The Swiss mathematician Leonhard Euler pioneered the modern approach to congruence in about 1750, when he explicitly introduced the idea of congruence modulo
a number N.
Modular arithmetic was further advanced by Carl Friedrich Gauss
in his book Disquisitiones Arithmeticae
, published in 1801.
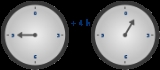
 A familiar use of modular arithmetic is in the 12-hour clock
A familiar use of modular arithmetic is in the 12-hour clock
, in which the day is divided into two 12-hour periods. If the time is 7:00 now, then 8 hours later it will be 3:00. Usual addition would suggest that the later time should be 7 + 8 = 15, but this is not the answer because clock time "wraps around" every 12 hours; in 12-hour time, there is no "15 o'clock". Likewise, if the clock starts at 12:00 (noon) and 21 hours elapse, then the time will be 9:00 the next day, rather than 33:00. Since the hour number starts over after it reaches 12, this is arithmetic modulo 12. 12 is congruent not only to 12 itself, but also to 0, so the time called "12:00" could also be called "0:00", since 0 ≡ 12 mod 12.
on the integer
s that is compatible with the operations of the ring
of integers: addition
, subtraction
, and multiplication
. For a positive integer n, two integers a and b are said to be congruent modulo n, written:

if their difference a − b is an integer multiple
of n. The number n is called the modulus of the congruence.
For example,

because 38 − 2 = 36, which is a multiple of 12.
The same rule holds for negative values:



When and
and  are either both positive or both negative, then
are either both positive or both negative, then  can also be thought of as asserting that both
can also be thought of as asserting that both  and
and  have the same remainder
have the same remainder
. For instance:

because both and
and  have the same remainder,
have the same remainder,  . It is also the case that
. It is also the case that  is an integer multiple of
is an integer multiple of  , which agrees with the prior definition of the congruence relation.
, which agrees with the prior definition of the congruence relation.
A remark on the notation: Because it is common to consider several congruence relations for different moduli at the same time, the modulus is incorporated in the notation. In spite of the ternary notation, the congruence relation for a given modulus is binary
. This would have been clearer if the notation a n b had been used, instead of the common traditional notation.
The properties that make this relation a congruence relation (respecting addition, subtraction, and multiplication) are the following.
If

and

then:
It should be noted that the above two properties would still hold if the theory were expanded to include all real numbers, that is if were not necessarily all integers. The next property, however, would fail if these variables were not all integers:
were not necessarily all integers. The next property, however, would fail if these variables were not all integers:
, and the equivalence class of the integer a, denoted by , is the set
, is the set  . This set, consisting of the integers congruent to a modulo n, is called the congruence class or residue class or simply residue of the integer a, modulo n. When the modulus n is known from the context, that residue may also be denoted
. This set, consisting of the integers congruent to a modulo n, is called the congruence class or residue class or simply residue of the integer a, modulo n. When the modulus n is known from the context, that residue may also be denoted  .
.
The set of all congruence classes modulo n is denoted or
or  (the alternate notation
(the alternate notation  is not recommended because of the possible confusion with the set of n-adic integers). It is defined by:
is not recommended because of the possible confusion with the set of n-adic integers). It is defined by:

When n ≠ 0, has n elements, and can be written as:
has n elements, and can be written as:

When n = 0, does not have zero elements; rather, it is isomorphic
does not have zero elements; rather, it is isomorphic
to , since
, since  .
.
We can define addition, subtraction, and multiplication on by the following rules:
by the following rules:
The verification that this is a proper definition uses the properties given before.
In this way, becomes a commutative ring
becomes a commutative ring
. For example, in the ring , we have
, we have
as in the arithmetic for the 24-hour clock.
The notation is used, because it is the factor ring of
is used, because it is the factor ring of  by the ideal
by the ideal  containing all integers divisible by n, where
containing all integers divisible by n, where  is the singleton set
is the singleton set  . Thus
. Thus  is a field
is a field
when is a maximal ideal
is a maximal ideal
, that is, when is prime.
is prime.
In terms of groups, the residue class is the coset
is the coset
of a in the quotient group
 , a cyclic group
, a cyclic group
.
The set has a number of important mathematical properties that are foundational to various branches of mathematics.
has a number of important mathematical properties that are foundational to various branches of mathematics.
Rather than excluding the special case n = 0, it is more useful to include (which, as mentioned before, is isomorphic to the ring
(which, as mentioned before, is isomorphic to the ring  of integers), for example when discussing the characteristic
of integers), for example when discussing the characteristic
of a ring
.
in division
. The operation of finding the remainder is sometimes referred to as the modulo operation
and we may see . The difference is in the use of congruency, indicated by "≡", and equality indicated by "=". Equality implies specifically the "common residue", the least non-negative member of an equivalence class. When working with modular arithmetic, each equivalence class is usually represented by its common residue, for example which can be found using long division
. It follows that, while it is correct to say , and , it is incorrect to say (with "=" rather than "≡").
The difference is clearest when dividing a negative number, since in that case remainders are negative. Hence to express the remainder we would have to write , rather than , since equivalence can only be said of common residues with the same sign.
In computer science
, it is the remainder operator that is usually indicated by either "%" (e.g. in C
, Java
, Javascript
, Perl
and Python
) or "mod" (e.g. in Pascal
, BASIC
, SQL
, Haskell
), with exceptions (e.g. Excel). These operators are commonly pronounced as "mod", but it is specifically a remainder that is computed (since in C++ negative number will be returned if the first argument is negative, and in Python a negative number will be returned if the second argument is negative). The function modulo instead of mod, like 38 ≡ 14 (modulo 12) is sometimes used to indicate the common residue rather than a remainder (e.g. in Ruby
).
Parentheses are sometimes dropped from the expression, e.g. or , or placed around the divisor e.g. . Notation such as has also been observed, but is ambiguous without contextual clarification.
. If b ≡ a (mod n), where n > 0, then if the remainder b is calculated
where is the largest integer less than or equal to
is the largest integer less than or equal to  , then
, then
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, modular arithmetic (sometimes called clock arithmetic) is a system of arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
for integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, where numbers "wrap around" after they reach a certain value—the modulus.
The Swiss mathematician Leonhard Euler pioneered the modern approach to congruence in about 1750, when he explicitly introduced the idea of congruence modulo
Modulo
In the mathematical community, the word modulo is often used informally. Generally, to say "A is the same as B modulo C" means, more-or-less, "A and B are the same except for differences accounted for or explained by C"....
a number N.
Modular arithmetic was further advanced by Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
in his book Disquisitiones Arithmeticae
Disquisitiones Arithmeticae
The Disquisitiones Arithmeticae is a textbook of number theory written in Latin by Carl Friedrich Gauss in 1798 when Gauss was 21 and first published in 1801 when he was 24...
, published in 1801.

12-hour clock
The 12-hour clock is a time conversion convention in which the 24 hours of the day are divided into two periods called ante meridiem and post meridiem...
, in which the day is divided into two 12-hour periods. If the time is 7:00 now, then 8 hours later it will be 3:00. Usual addition would suggest that the later time should be 7 + 8 = 15, but this is not the answer because clock time "wraps around" every 12 hours; in 12-hour time, there is no "15 o'clock". Likewise, if the clock starts at 12:00 (noon) and 21 hours elapse, then the time will be 9:00 the next day, rather than 33:00. Since the hour number starts over after it reaches 12, this is arithmetic modulo 12. 12 is congruent not only to 12 itself, but also to 0, so the time called "12:00" could also be called "0:00", since 0 ≡ 12 mod 12.
Congruence relation
Modular arithmetic can be handled mathematically by introducing a congruence relationCongruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
on the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s that is compatible with the operations of the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of integers: addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
, and multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
. For a positive integer n, two integers a and b are said to be congruent modulo n, written:

if their difference a − b is an integer multiple
Multiple (mathematics)
In mathematics, a multiple is the product of any quantity and an integer. In other words, for the quantities a and b, we say that b is a multiple of a if b = na for some integer n , which is called the multiplier or coefficient. If a is not zero, this is equivalent to saying that b/a is an integer...
of n. The number n is called the modulus of the congruence.
For example,

because 38 − 2 = 36, which is a multiple of 12.
The same rule holds for negative values:



When
 and
and  are either both positive or both negative, then
are either both positive or both negative, then  can also be thought of as asserting that both
can also be thought of as asserting that both  and
and  have the same remainder
have the same remainderRemainder
In arithmetic, the remainder is the amount "left over" after the division of two integers which cannot be expressed with an integer quotient....
. For instance:

because both
 and
and  have the same remainder,
have the same remainder,  . It is also the case that
. It is also the case that  is an integer multiple of
is an integer multiple of  , which agrees with the prior definition of the congruence relation.
, which agrees with the prior definition of the congruence relation.A remark on the notation: Because it is common to consider several congruence relations for different moduli at the same time, the modulus is incorporated in the notation. In spite of the ternary notation, the congruence relation for a given modulus is binary
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
. This would have been clearer if the notation a n b had been used, instead of the common traditional notation.
The properties that make this relation a congruence relation (respecting addition, subtraction, and multiplication) are the following.
If

and

then:
It should be noted that the above two properties would still hold if the theory were expanded to include all real numbers, that is if
 were not necessarily all integers. The next property, however, would fail if these variables were not all integers:
were not necessarily all integers. The next property, however, would fail if these variables were not all integers:Ring of congruence classes
Like any congruence relation, congruence modulo n is an equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
, and the equivalence class of the integer a, denoted by
 , is the set
, is the set  . This set, consisting of the integers congruent to a modulo n, is called the congruence class or residue class or simply residue of the integer a, modulo n. When the modulus n is known from the context, that residue may also be denoted
. This set, consisting of the integers congruent to a modulo n, is called the congruence class or residue class or simply residue of the integer a, modulo n. When the modulus n is known from the context, that residue may also be denoted  .
.The set of all congruence classes modulo n is denoted
 or
or  (the alternate notation
(the alternate notation  is not recommended because of the possible confusion with the set of n-adic integers). It is defined by:
is not recommended because of the possible confusion with the set of n-adic integers). It is defined by:
When n ≠ 0,
 has n elements, and can be written as:
has n elements, and can be written as:
When n = 0,
 does not have zero elements; rather, it is isomorphic
does not have zero elements; rather, it is isomorphicIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to
 , since
, since  .
.We can define addition, subtraction, and multiplication on
 by the following rules:
by the following rules:The verification that this is a proper definition uses the properties given before.
In this way,
 becomes a commutative ring
becomes a commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
. For example, in the ring
 , we have
, we have
as in the arithmetic for the 24-hour clock.
The notation
 is used, because it is the factor ring of
is used, because it is the factor ring of  by the ideal
by the ideal  containing all integers divisible by n, where
containing all integers divisible by n, where  is the singleton set
is the singleton set  . Thus
. Thus  is a field
is a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
when
 is a maximal ideal
is a maximal idealMaximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
, that is, when
 is prime.
is prime.In terms of groups, the residue class
 is the coset
is the cosetCoset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
of a in the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
 , a cyclic group
, a cyclic groupCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
.
The set
 has a number of important mathematical properties that are foundational to various branches of mathematics.
has a number of important mathematical properties that are foundational to various branches of mathematics.Rather than excluding the special case n = 0, it is more useful to include
 (which, as mentioned before, is isomorphic to the ring
(which, as mentioned before, is isomorphic to the ring  of integers), for example when discussing the characteristic
of integers), for example when discussing the characteristicCharacteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
of a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
.
Remainders
The notion of modular arithmetic is related to that of the remainderRemainder
In arithmetic, the remainder is the amount "left over" after the division of two integers which cannot be expressed with an integer quotient....
in division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
. The operation of finding the remainder is sometimes referred to as the modulo operation
Modulo operation
In computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n...
and we may see . The difference is in the use of congruency, indicated by "≡", and equality indicated by "=". Equality implies specifically the "common residue", the least non-negative member of an equivalence class. When working with modular arithmetic, each equivalence class is usually represented by its common residue, for example which can be found using long division
Long division
In arithmetic, long division is a standard procedure suitable for dividing simple or complex multidigit numbers. It breaks down a division problem into a series of easier steps. As in all division problems, one number, called the dividend, is divided by another, called the divisor, producing a...
. It follows that, while it is correct to say , and , it is incorrect to say (with "=" rather than "≡").
The difference is clearest when dividing a negative number, since in that case remainders are negative. Hence to express the remainder we would have to write , rather than , since equivalence can only be said of common residues with the same sign.
In computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, it is the remainder operator that is usually indicated by either "%" (e.g. in C
C (programming language)
C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
, Java
Java (programming language)
Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
, Javascript
JavaScript
JavaScript is a prototype-based scripting language that is dynamic, weakly typed and has first-class functions. It is a multi-paradigm language, supporting object-oriented, imperative, and functional programming styles....
, Perl
Perl
Perl is a high-level, general-purpose, interpreted, dynamic programming language. Perl was originally developed by Larry Wall in 1987 as a general-purpose Unix scripting language to make report processing easier. Since then, it has undergone many changes and revisions and become widely popular...
and Python
Python (programming language)
Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
) or "mod" (e.g. in Pascal
Pascal (programming language)
Pascal is an influential imperative and procedural programming language, designed in 1968/9 and published in 1970 by Niklaus Wirth as a small and efficient language intended to encourage good programming practices using structured programming and data structuring.A derivative known as Object Pascal...
, BASIC
BASIC
BASIC is a family of general-purpose, high-level programming languages whose design philosophy emphasizes ease of use - the name is an acronym from Beginner's All-purpose Symbolic Instruction Code....
, SQL
SQL
SQL is a programming language designed for managing data in relational database management systems ....
, Haskell
Haskell (programming language)
Haskell is a standardized, general-purpose purely functional programming language, with non-strict semantics and strong static typing. It is named after logician Haskell Curry. In Haskell, "a function is a first-class citizen" of the programming language. As a functional programming language, the...
), with exceptions (e.g. Excel). These operators are commonly pronounced as "mod", but it is specifically a remainder that is computed (since in C++ negative number will be returned if the first argument is negative, and in Python a negative number will be returned if the second argument is negative). The function modulo instead of mod, like 38 ≡ 14 (modulo 12) is sometimes used to indicate the common residue rather than a remainder (e.g. in Ruby
Ruby (programming language)
Ruby is a dynamic, reflective, general-purpose object-oriented programming language that combines syntax inspired by Perl with Smalltalk-like features. Ruby originated in Japan during the mid-1990s and was first developed and designed by Yukihiro "Matz" Matsumoto...
).
Parentheses are sometimes dropped from the expression, e.g. or , or placed around the divisor e.g. . Notation such as has also been observed, but is ambiguous without contextual clarification.
Functional representation of the remainder operation
The remainder operation can be represented using the floor functionFloor function
In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
. If b ≡ a (mod n), where n > 0, then if the remainder b is calculated

where
 is the largest integer less than or equal to
is the largest integer less than or equal to  , then
, then
-

If instead a remainder b in the range −n ≤ b < 0 is required, then
Residue systems
Each residue class modulo n may be represented by any one of its members, although we usually represent each residue class by the smallest nonnegative integer which belongs to that class (since this is the proper remainder which results from division). Note that any two members of different residue classes modulo n are incongruent modulo n. Furthermore, every integer belongs to one and only one residue class modulo n.
The set of integers {0, 1, 2, ..., n - 1} is called the least residue system modulo n. Any set of n integers, no two of which are congruent modulo n, is called a complete residue system modulo n.
It is clear that the least residue system is a complete residue system, and that a complete residue system is simply a set containing precisely one representative of each residue class modulo n. The least residue system modulo 4 is {0, 1, 2, 3}. Some other complete residue systems modulo 4 are:
- {1,2,3,4}
- {13,14,15,16}
- {-2,-1,0,1}
- {-13,4,17,18}
- {-5,0,6,21}
- {27,32,37,42}
Some sets which are not complete residue systems modulo 4 are:
- {-5,0,6,22} since 6 is congruent to 22 modulo 4.
- {5,15} since a complete residue system modulo 4 must have exactly 4 incongruent residue classes.
Reduced residue systems
Any set of φ(n) integers that are relatively prime to n and that are mutually incongruent modulo n, where φ(n) denotes Euler's totient functionEuler's totient functionIn number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
, is called a reduced residue system modulo n. The example above, {5,15} is an example of a reduced residue system modulo 4.
Applications
Modular arithmetic is referenced in number theoryNumber theoryNumber theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, group theoryGroup theoryIn mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, ring theoryRing theoryIn abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, knot theoryKnot theoryIn topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, abstract algebraAbstract algebraAbstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, cryptographyCryptographyCryptography is the practice and study of techniques for secure communication in the presence of third parties...
, computer scienceComputer scienceComputer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, chemistryChemistryChemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
and the visualVisual artsThe visual arts are art forms that create works which are primarily visual in nature, such as ceramics, drawing, painting, sculpture, printmaking, design, crafts, and often modern visual arts and architecture...
and musicMusicMusic is an art form whose medium is sound and silence. Its common elements are pitch , rhythm , dynamics, and the sonic qualities of timbre and texture...
al arts.
It is one of the foundations of number theory, touching on almost every aspect of its study, and provides key examples for group theory, ring theory and abstract algebra.
Modular arithmetic is often used to calculate checksums that are used within identifiers - International Bank Account NumberInternational Bank Account NumberThe International Bank Account Number is an international standard for identifying bank accounts across national borders with a minimal risk of propagating transcription errors. It was originally adopted by the European Committee for Banking Standards , and was later adopted as an international...
s (IBANs) for example make use of modulo 97 arithmetic to trap user input errors in bank account numbers.
In cryptography, modular arithmetic directly underpins public keyPublic-key cryptographyPublic-key cryptography refers to a cryptographic system requiring two separate keys, one to lock or encrypt the plaintext, and one to unlock or decrypt the cyphertext. Neither key will do both functions. One of these keys is published or public and the other is kept private...
systems such as RSA and Diffie-HellmanDiffie-Hellman key exchangeDiffie–Hellman key exchange Synonyms of Diffie–Hellman key exchange include:*Diffie–Hellman key agreement*Diffie–Hellman key establishment*Diffie–Hellman key negotiation...
, as well as providing finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s which underlie elliptic curveElliptic curveIn mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s, and is used in a variety of symmetric key algorithms including AESAdvanced Encryption StandardAdvanced Encryption Standard is a specification for the encryption of electronic data. It has been adopted by the U.S. government and is now used worldwide. It supersedes DES...
, IDEAInternational Data Encryption AlgorithmIn cryptography, the International Data Encryption Algorithm is a block cipher designed by James Massey of ETH Zurich and Xuejia Lai and was first described in 1991. As a block cipher, it is also symmetric. The algorithm was intended as a replacement for the Data Encryption Standard[DES]...
, and RC4RC4In cryptography, RC4 is the most widely used software stream cipher and is used in popular protocols such as Secure Sockets Layer and WEP...
.
In computer science, modular arithmetic is often applied in bitwise operationBitwise operationA bitwise operation operates on one or more bit patterns or binary numerals at the level of their individual bits. This is used directly at the digital hardware level as well as in microcode, machine code and certain kinds of high level languages...
s and other operations involving fixed-width, cyclic data structureData structureIn computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
s. The modulo operationModulo operationIn computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n...
, as implemented in many programming languageProgramming languageA programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s and calculatorCalculatorAn electronic calculator is a small, portable, usually inexpensive electronic device used to perform the basic operations of arithmetic. Modern calculators are more portable than most computers, though most PDAs are comparable in size to handheld calculators.The first solid-state electronic...
s, is an application of modular arithmetic that is often used in this context. XOR is the sum of 2 bits, modulo 2.
In chemistry, the last digit of the CAS registry numberCAS registry numberCAS Registry Numbersare unique numerical identifiers assigned by the "Chemical Abstracts Service" toevery chemical described in the...
(a number which is unique for each chemical compound) is a check digitCheck digitA check digit is a form of redundancy check used for error detection, the decimal equivalent of a binary checksum. It consists of a single digit computed from the other digits in the message....
, which is calculated by taking the last digit of the first two parts of the CAS registry numberCAS registry numberCAS Registry Numbersare unique numerical identifiers assigned by the "Chemical Abstracts Service" toevery chemical described in the...
times 1, the next digit times 2, the next digit times 3 etc., adding all these up and computing the sum modulo 10.
In music, arithmetic modulo 12 is used in the consideration of the system of twelve-tone equal temperament, where octaveOctaveIn music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...
and enharmonicEnharmonicIn modern musical notation and tuning, an enharmonic equivalent is a note , interval , or key signature which is equivalent to some other note, interval, or key signature, but "spelled", or named, differently...
equivalency occurs (that is, pitches in a 1∶2 or 2∶1 ratio are equivalent, and C-sharpSharp (music)In music, sharp, dièse , or diesis means higher in pitch and the sharp symbol raises a note by a half tone. Intonation may be flat, sharp, or both, successively or simultaneously...
is considered the same as D-flat).
The method of casting out ninesCasting out ninesCasting out nines is a sanity check to ensure that hand computations of sums, differences, products, and quotients of integers are correct. By looking at the digital roots of the inputs and outputs, the casting-out-nines method can help one check arithmetic calculations...
offers a quick check of decimal arithmetic computations performed by hand. It is based on modular arithmetic modulo 9, and specifically on the crucial property that 10 ≡ 1 (mod 9).
Arithmetic modulo 7 is especially important in determining the day of the week in the Gregorian calendarGregorian calendarThe Gregorian calendar, also known as the Western calendar, or Christian calendar, is the internationally accepted civil calendar. It was introduced by Pope Gregory XIII, after whom the calendar was named, by a decree signed on 24 February 1582, a papal bull known by its opening words Inter...
. In particular, Zeller's congruenceZeller's congruenceZeller's congruence is an algorithm devised by Christian Zeller to calculate the day of the week for any Julian or Gregorian calendar date.- Formula :For the Gregorian calendar, Zeller's congruence is...
and the doomsday algorithm make heavy use of modulo-7 arithmetic.
More generally, modular arithmetic also has application in disciplines such as lawLawLaw is a system of rules and guidelines which are enforced through social institutions to govern behavior, wherever possible. It shapes politics, economics and society in numerous ways and serves as a social mediator of relations between people. Contract law regulates everything from buying a bus...
(see e.g., apportionmentApportionmentThe legal term apportionment means distribution or allotment in proper shares.It is a term used in law in a variety of senses...
), economicsEconomicsEconomics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, (see e.g., game theoryGame theoryGame theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
) and other areas of the social sciencesSocial sciencesSocial science is the field of study concerned with society. "Social science" is commonly used as an umbrella term to refer to a plurality of fields outside of the natural sciences usually exclusive of the administrative or managerial sciences...
, where proportionalProportional (fair division)Proportional division or simple fair division is the original and simplest problem in fair division. Fair division problems are also called cake-cutting problems. A proportional division of a cake between N people would ensure each of them got at least 1/N of the cake by their own valuation...
division and allocation of resources plays a central part of the analysis.
Computational complexity
Since modular arithmetic has such a wide range of applications, it is important to know how hard it is to solve a system of congruences. A linear system of congruences can be solved in polynomial time with a form of Gaussian eliminationGaussian eliminationIn linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
, for details see linear congruence theorem. Algorithms, such as Montgomery reductionMontgomery reductionIn arithmetic computation, Montgomery reduction is an algorithm introduced in 1985 by Peter Montgomery that allows modular arithmetic to be performed efficiently when the modulus is large ....
, also exist to allow simple arithmetic operations, such as multiplication and exponentiation modulo nModular exponentiationModular exponentiation is a type of exponentiation performed over a modulus. It is particularly useful in computer science, especially in the field of cryptography....
, to be performed efficiently on large numbers.
Solving a system of non-linear modular arithmetic equations is NP-completeNP-completeIn computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
.
See also
- Boolean ringBoolean ringIn mathematics, a Boolean ring R is a ring for which x2 = x for all x in R; that is, R consists only of idempotent elements....
- Circular bufferCircular bufferA circular buffer, cyclic buffer or ring buffer is a data structure that uses a single, fixed-size buffer as if it were connected end-to-end.This structure lends itself easily to buffering data streams.-Uses:...
circular math memory addressing - Congruence relationCongruence relationIn abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
- DivisionDivision (mathematics)right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
- Finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
- Legendre symbolLegendre symbolIn number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
- Modular exponentiationModular exponentiationModular exponentiation is a type of exponentiation performed over a modulus. It is particularly useful in computer science, especially in the field of cryptography....
- Modular multiplicative inverse
- Modulo operationModulo operationIn computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n...
- Pisano periodPisano periodIn number theory, the nth Pisano period, written π, is the period with which the sequence of Fibonacci numbers, modulo n repeats. For example, the Fibonacci numbers modulo 3 are , 1, 1, 2, 0, 2, 2, 1, 0, 1, 1, etc., with the first eight numbers repeating, so π = 8.Pisano periods are named after...
(Fibonacci sequences modulo n) - Primitive rootPrimitive root modulo nIn modular arithmetic, a branch of number theory, a primitive root modulo n is any number g with the property that any number coprime to n is congruent to a power of g modulo n. In other words, g is a generator of the multiplicative group of integers modulo n...
- Quadratic reciprocityQuadratic reciprocityIn number theory, the law of quadratic reciprocity is a theorem about modular arithmetic which gives conditions for the solvability of quadratic equations modulo prime numbers...
- Quadratic residue
- Number theoryNumber theoryNumber theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
- Reduced residue systemReduced residue systemAny subset R of the set of integers is called a reduced residue system modulo n if#gcd = 1 for each r contained in R;#R contains φ elements;#no two elements of R are congruent modulo n....
- Two-element Boolean algebra
- Serial number arithmetic (a special case of modular arithmetic)
- Topics relating to the group theory behind modular arithmetic:
- Cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
- Multiplicative group of integers modulo nMultiplicative group of integers modulo nIn modular arithmetic the set of congruence classes relatively prime to the modulus n form a group under multiplication called the multiplicative group of integers modulo n. It is also called the group of primitive residue classes modulo n. In the theory of rings, a branch of abstract algebra, it...
- Cyclic group
- Other important theorems relating to modular arithmetic:
- Carmichael's theorem
- Chinese remainder theoremChinese remainder theoremThe Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
- Euler's theorem
- Fermat's little theoremFermat's little theoremFermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
(a special case of Euler's theorem) - Lagrange's theoremLagrange's theorem (group theory)Lagrange's theorem, in the mathematics of group theory, states that for any finite group G, the order of every subgroup H of G divides the order of G. The theorem is named after Joseph Lagrange....
External links
- In this modular art article, one can learn more about applications of modular arithmetic in art.
- An article on modular arithmetic on the GIMPS wiki
- Modular Arithmetic and patterns in addition and multiplication tables
- Whitney Music Box—an audio/video demonstration of integer modular math
- Automated modular arithmetic theorem provers:







