
Multiplication
Encyclopedia
Multiplication (often denoted by the cross symbol
"") is the mathematical operation
of scaling one number by another. It is one of the four basic operations in elementary arithmetic
(the others being addition
, subtraction
and division
).
Because the result of scaling by whole numbers
can be thought of as consisting of some number of copies of the original, whole-number products greater than 1 can be computed by repeated addition; for example, 3 multiplied by 4 (often said as "3 times 4") can be calculated by adding 4 copies of 3 together:

Here 3 and 4 are the "factors" and 12 is the "product".
There are differences amongst educationalists as to which number should normally be considered as the number of copies and whether multiplication should even be introduced as repeated addition. For example 3 multiplied by 4 can also be calculated by adding 3 copies of 4 together:

Multiplication of rational number
s (fractions) and real number
s is defined by systematic generalization of this basic idea.
Multiplication can also be visualized as counting objects arranged in a rectangle
(for whole numbers) or as finding the area
of a rectangle whose sides have given length
s (for numbers generally). The area of a rectangle does not depend on which side is measured first which illustrates that the order in which numbers are multiplied together does not matter.
In general the result of multiplying two measurements gives a result of a new type depending on the measurements. For instance:


The inverse operation of multiplication is division. For example, 4 multiplied by 3 equals 12. Then 12 divided by 3 equals 4. Multiplication by 3, followed by division by 3, yields the original number.
Multiplication is also defined for other types of numbers (such as complex number
s), and for more abstract constructs such as matrices
. For these more abstract constructs, the order in which the operands are multiplied sometimes does matter.
 Multiplication is often written using the multiplication sign "×" between the terms; that is, in infix notation
Multiplication is often written using the multiplication sign "×" between the terms; that is, in infix notation
. The result is expressed with an equals sign
. For example,
 (verbally, "two times three equals six")
(verbally, "two times three equals six")



There are several other common notations for multiplication. Many of these are intended to reduce confusion between the multiplication sign × and the commonly used variable x:

The numbers to be multiplied are generally called the "factors
" or "multiplicands". When thinking of multiplication as repeated addition, the number to be multiplied is called the "multiplicand", while the number of multiples is called the "multiplier". In algebra, a number that is the multiplier of a variable or expression (e.g. the 3 in 3xy2) is called a coefficient
.
The result of a multiplication is called a product
, and is a multiple
of each factor if the other factor is an integer. For example, 15 is the product of 3 and 5, and is both a multiple of 3 and a multiple of 5.
of memorized or consulted products of small numbers (typically any two numbers from 0 to 9), however one method, the peasant multiplication
algorithm, does not.
Multiplying numbers to more than a couple of decimal places by hand is tedious and error prone. Common logarithm
s were invented to simplify such calculations. The slide rule
allowed numbers to be quickly multiplied to about three places of accuracy. Beginning in the early twentieth century, mechanical calculator
s, such as the Marchant
, automated multiplication of up to 10 digit numbers. Modern electronic computer
s and calculators have greatly reduced the need for multiplication by hand.
, Greek
, Indian
and Chinese civilizations.
The Ishango bone
, dated to about 18,000 to 20,000 BC, hints at a knowledge of multiplication in the Upper Paleolithic
era in Central Africa
.
s. These tables consisted of a list of the first twenty multiples of a certain principal number n: n, 2n, ..., 20n; followed by the multiples of 10n: 30n 40n, and 50n. Then to compute any sexagesimal product, say 53n, one only needed to add 50n and 3n computed from the table.
involving place value addition, subtraction, multiplication and division. These place value decimal arithmetic algorithms were introduced by Al Khwarizmi to Arab countries in the early 9th century.
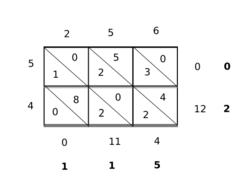 The modern method of multiplication based on the Hindu–Arabic numeral system
The modern method of multiplication based on the Hindu–Arabic numeral system
was first described by Brahmagupta
. Brahmagupta gave rules for addition, subtraction, multiplication and division. Henry Burchard Fine
, then professor of Mathematics at Princeton University
, wrote the following:
s have been designed which reduce the computation time considerably when multiplying large numbers. In particular for very large numbers methods based on the Discrete Fourier Transform can reduce the number of simple multiplications to the order of n log2(n).
. This analysis is routinely applied in physics but has also found applications in finance. One can only meaningfully add or subtract quantities of the same type but can multiply or divide quantities of different types.
A common example is multiplying speed by time gives distance, so
. Unicode position U+220F (∏) contains a glyph for denoting such a product, distinct from U+03A0 (Π), the letter. The meaning of this notation is given by:
The subscript gives the symbol for a dummy variable
(i in this case), called the "index of multiplication" together with its lower bound (m), whereas the superscript (here n) gives its upper bound. The lower and upper bound are expressions denoting integers. The factors of the product are obtained by taking the expression following the product operator, with successive integer values substituted for the index of multiplication, starting from the lower bound and incremented by 1 up to and including the upper bound. So, for example:
In case m = n, the value of the product is the same as that of the single factor xm. If m > n, the product is the empty product
, with the value 1.
∞. The product of such a series is defined as the limit
of the product of the first n terms, as n grows without bound. That is, by definition,
One can similarly replace m with negative infinity, and define:

provided both limits exist.
Commutative property
Associative property
Distributive property
Identity element
Zero element
There are a number of further properties of multiplication not satisfied by all types of numbers.
Negation
Inverse element
Order preservation
Other mathematical systems that include a multiplication operation may not have all these properties. For example, multiplication is not, in general, commutative for matrices and quaternion
s.
proposed axioms for arithmetic based on his axioms for natural numbers. Peano arithmetic has two axioms for multiplication:


Here S(y) represents the successor
of y, or the natural number which follows y. The various properties like associativity can be proved from these and the other axioms of Peano arithmetic including induction
. For instance S(0). denoted by 1, is a multiplicative identity because

The axioms for integer
s typically define them as equivalence classes of ordered pairs of natural numbers. The model is based on treating (x,y) as equivalent to x−y when x and y are treated as integers. Thus both (0,1) and (1,2) are equivalent to −1. The multiplication axiom for integers defined this way is

The rule that −1 × −1 = 1 can then be deduced from

Multiplication is extended in a similar way to rational number
s and then to real number
s.
provides a way to arrive at a set-theoretic interpretation of multiplication of cardinal numbers. In the expression
if the n copies of a are to be combined in disjoint union then clearly they must be made disjoint; an obvious way to do this is to use either a or n as the indexing set for the other. Then, the members of are exactly those of the Cartesian product
are exactly those of the Cartesian product
 . The properties of the multiplicative operation as applying to natural numbers then follow trivially from the corresponding properties of the Cartesian product.
. The properties of the multiplicative operation as applying to natural numbers then follow trivially from the corresponding properties of the Cartesian product.
structure. These axioms are closure, associativity, and the inclusion of an identity element and inverses.
A simple example is the set of non-zero rational numbers. Here we have identity 1, as opposed to groups under addition where the identity is typically 0. Note that with the rationals, we must exclude zero because, under multiplication, it does not have an inverse: there is no rational number that can be multiplied by zero to result in 1. In this example we have an abelian group
, but that is not always the case.
To see this, look at the set of invertible square matrices of a given dimension, over a given field
. Now it is straightforward to verify closure, associativity, and inclusion of identity (the identity matrix
) and inverses. However, matrix multiplication is not commutative, therefore this group is nonabelian.
Another fact of note is that the integers under multiplication is not a group, even if we exclude zero. This is easily seen by the nonexistence of an inverse for all elements other than 1 and -1.
Multiplication in group theory is typically notated either by a dot, or by juxtaposition (the omission of an operation symbol between elements). So multiplying element a by element b could be notated a b or ab. When referring to a group via the indication of the set and operation, the dot is used, e.g. our first example could be indicated by
b or ab. When referring to a group via the indication of the set and operation, the dot is used, e.g. our first example could be indicated by 
) or do not look much like numbers (such as quaternion
s).
Integers is the sum of M copies of N when N and M are positive whole numbers. This gives the number of things in an array N wide and M high. Generalization to negative numbers can be done by
is the sum of M copies of N when N and M are positive whole numbers. This gives the number of things in an array N wide and M high. Generalization to negative numbers can be done by  and
and  . The same sign rules apply to rational and real numbers.
. The same sign rules apply to rational and real numbers.
Rational number
s
Real number
s is the limit of the products of the corresponding terms in certain sequences of rationals that converge to x and y, respectively, and is significant in calculus
is the limit of the products of the corresponding terms in certain sequences of rationals that converge to x and y, respectively, and is significant in calculus
. This gives the area of a rectangle x high and y wide. See Products of sequences, above.
Complex number
s
Further generalizations
Division

indicates that the base a to be multiplied by itself n times.
×
The multiplication sign is the symbol ×. The symbol is similar to the lowercase letter x but is a more symmetric saltire, and has different uses. It is also known as St...
"") is the mathematical operation
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
of scaling one number by another. It is one of the four basic operations in elementary arithmetic
Elementary arithmetic
Elementary arithmetic is the simplified portion of arithmetic which is considered necessary and appropriate during primary education. It includes the operations of addition, subtraction, multiplication, and division. It is taught in elementary school....
(the others being addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
and division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
).
Because the result of scaling by whole numbers
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
can be thought of as consisting of some number of copies of the original, whole-number products greater than 1 can be computed by repeated addition; for example, 3 multiplied by 4 (often said as "3 times 4") can be calculated by adding 4 copies of 3 together:

Here 3 and 4 are the "factors" and 12 is the "product".
There are differences amongst educationalists as to which number should normally be considered as the number of copies and whether multiplication should even be introduced as repeated addition. For example 3 multiplied by 4 can also be calculated by adding 3 copies of 4 together:

Multiplication of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s (fractions) and real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s is defined by systematic generalization of this basic idea.
Multiplication can also be visualized as counting objects arranged in a rectangle
Rectangle
In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
(for whole numbers) or as finding the area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
of a rectangle whose sides have given length
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
s (for numbers generally). The area of a rectangle does not depend on which side is measured first which illustrates that the order in which numbers are multiplied together does not matter.
In general the result of multiplying two measurements gives a result of a new type depending on the measurements. For instance:


The inverse operation of multiplication is division. For example, 4 multiplied by 3 equals 12. Then 12 divided by 3 equals 4. Multiplication by 3, followed by division by 3, yields the original number.
Multiplication is also defined for other types of numbers (such as complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s), and for more abstract constructs such as matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. For these more abstract constructs, the order in which the operands are multiplied sometimes does matter.
Notation and terminology

Infix notation
Infix notation is the common arithmetic and logical formula notation, in which operators are written infix-style between the operands they act on . It is not as simple to parse by computers as prefix notation or postfix notation Infix notation is the common arithmetic and logical formula notation,...
. The result is expressed with an equals sign
Equals sign
The equality sign, equals sign, or "=" is a mathematical symbol used to indicate equality. It was invented in 1557 by Robert Recorde. The equals sign is placed between the things stated to have the same value, as in an equation...
. For example,
 (verbally, "two times three equals six")
(verbally, "two times three equals six")


There are several other common notations for multiplication. Many of these are intended to reduce confusion between the multiplication sign × and the commonly used variable x:
- Multiplication is sometimes denoted by either a middle dot or a periodFull stopA full stop is the punctuation mark commonly placed at the end of sentences. In American English, the term used for this punctuation is period. In the 21st century, it is often also called a dot by young people...
:

- The middle dot is standard in the United StatesUnited StatesThe United States of America is a federal constitutional republic comprising fifty states and a federal district...
, the United KingdomUnited KingdomThe United Kingdom of Great Britain and Northern IrelandIn the United Kingdom and Dependencies, other languages have been officially recognised as legitimate autochthonous languages under the European Charter for Regional or Minority Languages...
, and other countries where the period is used as a decimal pointDecimal separatorDifferent symbols have been and are used for the decimal mark. The choice of symbol for the decimal mark affects the choice of symbol for the thousands separator used in digit grouping. Consequently the latter is treated in this article as well....
. In other countries that use a commaComma (punctuation)The comma is a punctuation mark. It has the same shape as an apostrophe or single closing quotation mark in many typefaces, but it differs from them in being placed on the baseline of the text. Some typefaces render it as a small line, slightly curved or straight but inclined from the vertical, or...
as a decimal point, either the period or a middle dot is used for multiplication.
- The asteriskAsteriskAn asterisk is a typographical symbol or glyph. It is so called because it resembles a conventional image of a star. Computer scientists and mathematicians often pronounce it as star...
(as in5*2) is often used in programming languageProgramming languageA programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s because it appears on every keyboard. This usage originated in the FORTRANFortranFortran is a general-purpose, procedural, imperative programming language that is especially suited to numeric computation and scientific computing...
programming language.
- In algebraAlgebraAlgebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, multiplication involving variablesVariable (mathematics)In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
is often written as a juxtaposition (e.g. xy for x times y or 5x for five times x). This notation can also be used for quantities that are surrounded by parentheses (e.g. 5(2) or (5)(2) for five times two).
- In matrix multiplicationMatrix multiplicationIn mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
, there is actually a distinction between the cross and the dot symbols. The cross symbol generally denotes a vector multiplication, while the dot denotes a scalar multiplication. A similar convention distinguishes between the cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
and the dot productDot productIn mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of two vectors.
The numbers to be multiplied are generally called the "factors
Factorization
In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...
" or "multiplicands". When thinking of multiplication as repeated addition, the number to be multiplied is called the "multiplicand", while the number of multiples is called the "multiplier". In algebra, a number that is the multiplier of a variable or expression (e.g. the 3 in 3xy2) is called a coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
.
The result of a multiplication is called a product
Product (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
, and is a multiple
Multiple (mathematics)
In mathematics, a multiple is the product of any quantity and an integer. In other words, for the quantities a and b, we say that b is a multiple of a if b = na for some integer n , which is called the multiplier or coefficient. If a is not zero, this is equivalent to saying that b/a is an integer...
of each factor if the other factor is an integer. For example, 15 is the product of 3 and 5, and is both a multiple of 3 and a multiple of 5.
Computation
The common methods for multiplying numbers using pencil and paper require a multiplication tableMultiplication table
In mathematics, a multiplication table is a mathematical table used to define a multiplication operation for an algebraic system....
of memorized or consulted products of small numbers (typically any two numbers from 0 to 9), however one method, the peasant multiplication
Ancient Egyptian multiplication
In mathematics, ancient Egyptian multiplication , one of two multiplication methods used by scribes, was a systematic method for multiplying two numbers that does not require the multiplication table, only the ability to multiply and divide by 2, and...
algorithm, does not.
Multiplying numbers to more than a couple of decimal places by hand is tedious and error prone. Common logarithm
Common logarithm
The common logarithm is the logarithm with base 10. It is also known as the decadic logarithm, named after its base. It is indicated by log10, or sometimes Log with a capital L...
s were invented to simplify such calculations. The slide rule
Slide rule
The slide rule, also known colloquially as a slipstick, is a mechanical analog computer. The slide rule is used primarily for multiplication and division, and also for functions such as roots, logarithms and trigonometry, but is not normally used for addition or subtraction.Slide rules come in a...
allowed numbers to be quickly multiplied to about three places of accuracy. Beginning in the early twentieth century, mechanical calculator
Calculator
An electronic calculator is a small, portable, usually inexpensive electronic device used to perform the basic operations of arithmetic. Modern calculators are more portable than most computers, though most PDAs are comparable in size to handheld calculators.The first solid-state electronic...
s, such as the Marchant
Marchant Calculator
The Marchant Calculating Machine Co. was founded in 1911 by Rodney and Alfred Marchant in Oakland, California.The company built mechanical, and then electromechanical calculators which had a reputation for reliability. First models were similar to the Odhner arithmometer. In 1918, employee Carl...
, automated multiplication of up to 10 digit numbers. Modern electronic computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
s and calculators have greatly reduced the need for multiplication by hand.
Historical algorithms
Methods of multiplication were documented in the EgyptianAncient Egypt
Ancient Egypt was an ancient civilization of Northeastern Africa, concentrated along the lower reaches of the Nile River in what is now the modern country of Egypt. Egyptian civilization coalesced around 3150 BC with the political unification of Upper and Lower Egypt under the first pharaoh...
, Greek
Ancient Greece
Ancient Greece is a civilization belonging to a period of Greek history that lasted from the Archaic period of the 8th to 6th centuries BC to the end of antiquity. Immediately following this period was the beginning of the Early Middle Ages and the Byzantine era. Included in Ancient Greece is the...
, Indian
Ancient India
Ancient India may refer to:* The ancient history of India, which generally includes the ancient history of the Asian Subcontinent, including:*Science and technology in ancient India**Indian mathematics**Astronomy**List of Indian inventions...
and Chinese civilizations.
The Ishango bone
Ishango bone
The Ishango bone is a bone tool, dated to the Upper Paleolithic era. It is a dark brown length of bone, the fibula of a baboon, with a sharp piece of quartz affixed to one end, perhaps for engraving...
, dated to about 18,000 to 20,000 BC, hints at a knowledge of multiplication in the Upper Paleolithic
Upper Paleolithic
The Upper Paleolithic is the third and last subdivision of the Paleolithic or Old Stone Age as it is understood in Europe, Africa and Asia. Very broadly it dates to between 40,000 and 10,000 years ago, roughly coinciding with the appearance of behavioral modernity and before the advent of...
era in Central Africa
Central Africa
Central Africa is a core region of the African continent which includes Burundi, the Central African Republic, Chad, the Democratic Republic of the Congo, and Rwanda....
.
Egyptians
The Egyptian method of multiplication of integers and fractions, documented in the Ahmes Papyrus, was by successive additions and doubling. For instance, to find the product of 13 and 21 one had to double 21 three times, obtaining 1 × 21 = 21, 2 × 21 = 42, 4 × 21 = 84, 8 × 21 = 168. The full product could then be found by adding the appropriate terms found in the doubling sequence:- 13 × 21 = (1 + 4 + 8) × 21 = (1 × 21) + (4 × 21) + (8 × 21) = 21 + 84 + 168 = 273.
Babylonians
The Babylonians used a sexagesimal positional number system, analogous to the modern day decimal system. Thus, Babylonian multiplication was very similar to modern decimal multiplication. Because of the relative difficulty of remembering 60 × 60 different products, Babylonian mathematicians employed multiplication tableMultiplication table
In mathematics, a multiplication table is a mathematical table used to define a multiplication operation for an algebraic system....
s. These tables consisted of a list of the first twenty multiples of a certain principal number n: n, 2n, ..., 20n; followed by the multiples of 10n: 30n 40n, and 50n. Then to compute any sexagesimal product, say 53n, one only needed to add 50n and 3n computed from the table.
Chinese
In the mathematical text Zhou Bi Suan Jing, dated prior to 300 BC, and the Nine Chapters on the Mathematical Art, multiplication calculations were written out in words, although the early Chinese mathematicians employed Rod calculusRod calculus
Rod calculus or rod calculation is the method of mathematical computation with counting rods in China from the Warring States to Ming dynasty before the counting rods were replaced by the more convenient and faster abacus.-Hardware:...
involving place value addition, subtraction, multiplication and division. These place value decimal arithmetic algorithms were introduced by Al Khwarizmi to Arab countries in the early 9th century.
Modern method

Hindu–Arabic numeral system
The Hindu–Arabic numeral system or Hindu numeral system is a positional decimal numeral system developed between the 1st and 5th centuries by Indian mathematicians, adopted by Persian and Arab mathematicians , and spread to the western world...
was first described by Brahmagupta
Brahmagupta
Brahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
. Brahmagupta gave rules for addition, subtraction, multiplication and division. Henry Burchard Fine
Henry Burchard Fine
Henry Burchard Fine was an American university dean and mathematician.Fine was born at Chambersburg, Pennsylvania, and was educated at Princeton and Leipzig universities...
, then professor of Mathematics at Princeton University
Princeton University
Princeton University is a private research university located in Princeton, New Jersey, United States. The school is one of the eight universities of the Ivy League, and is one of the nine Colonial Colleges founded before the American Revolution....
, wrote the following:
- The Indians are the inventors not only of the positional decimal system itself, but of most of the processes involved in elementary reckoning with the system. Addition and subtraction they performed quite as they are performed nowadays; multiplication they effected in many ways, ours among them, but division they did cumbrously.
Computer algorithms
The standard method of multiplying two n-digit numbers requires n2 simple multiplications. Multiplication algorithmMultiplication algorithm
A multiplication algorithm is an algorithm to multiply two numbers. Depending on the size of the numbers, different algorithms are in use...
s have been designed which reduce the computation time considerably when multiplying large numbers. In particular for very large numbers methods based on the Discrete Fourier Transform can reduce the number of simple multiplications to the order of n log2(n).
Products of measurements
When two measurements are multiplied together the product is of a type depending on the types of the measurements. The general theory is given by dimensional analysisDimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
. This analysis is routinely applied in physics but has also found applications in finance. One can only meaningfully add or subtract quantities of the same type but can multiply or divide quantities of different types.
A common example is multiplying speed by time gives distance, so
- 50 kilometers per hour × 3 hours = 150 kilometers.
Capital Pi notation
The product of a sequence of terms can be written with the product symbol, which derives from the capital letter Π (Pi) in the Greek alphabetGreek alphabet
The Greek alphabet is the script that has been used to write the Greek language since at least 730 BC . The alphabet in its classical and modern form consists of 24 letters ordered in sequence from alpha to omega...
. Unicode position U+220F (∏) contains a glyph for denoting such a product, distinct from U+03A0 (Π), the letter. The meaning of this notation is given by:
The subscript gives the symbol for a dummy variable
Free variables and bound variables
In mathematics, and in other disciplines involving formal languages, including mathematical logic and computer science, a free variable is a notation that specifies places in an expression where substitution may take place...
(i in this case), called the "index of multiplication" together with its lower bound (m), whereas the superscript (here n) gives its upper bound. The lower and upper bound are expressions denoting integers. The factors of the product are obtained by taking the expression following the product operator, with successive integer values substituted for the index of multiplication, starting from the lower bound and incremented by 1 up to and including the upper bound. So, for example:
In case m = n, the value of the product is the same as that of the single factor xm. If m > n, the product is the empty product
Empty product
In mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
, with the value 1.
Infinite products
One may also consider products of infinitely many terms; these are called infinite products. Notationally, we would replace n above by the lemniscateInfinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
∞. The product of such a series is defined as the limit
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
of the product of the first n terms, as n grows without bound. That is, by definition,
One can similarly replace m with negative infinity, and define:

provided both limits exist.
Properties
For the natural numbers, integers, fractions, and real and complex numbers, multiplication has certain properties:Commutative property
- The order in which two numbers are multiplied does not matter:
 .
.
Associative property
- Expressions solely involving multiplication are invariant with respect to order of operationsOrder of operationsIn mathematics and computer programming, the order of operations is a rule used to clarify unambiguously which procedures should be performed first in a given mathematical expression....
:
Distributive property
- Holds with respect to multiplication over addition. This identity is of prime importance in simplifying algebraic expressions:
Identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
- The multiplicative identity is 1; anything multiplied by one is itself. This is known as the identity property:
Zero element
Absorbing element
In mathematics, an absorbing element is a special type of element of a set with respect to a binary operation on that set. The result of combining an absorbing element with any element of the set is the absorbing element itself. In semigroup theory, the absorbing element is called a zero element...
- Any number multiplied by zero is zero. This is known as the zero property of multiplication:
- Zero is sometimes not included amongst the natural numbers.
There are a number of further properties of multiplication not satisfied by all types of numbers.
Negation
- Negative one times any number is equal to the opposite of that number.
- Negative one times negative one is positive one.
- The natural numbers do not include negative numbers.
Inverse element
Inverse element
In abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
- Every number x, except zero, has a multiplicative inverseMultiplicative inverseIn mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
, , such that
, such that  .
. - The natural numbers and integers do not have inverses.
Order preservation
- Multiplication by a positive number preserves orderOrder theoryOrder theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
: if a > 0, then if b > c then ab > ac. Multiplication by a negative number reverses order: if a < 0 and b > c then ab < ac. - The complex numbers do not have an order predicate.
Other mathematical systems that include a multiplication operation may not have all these properties. For example, multiplication is not, in general, commutative for matrices and quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s.
Axioms
In the book Arithmetices principia, nova methodo exposita, Giuseppe PeanoGiuseppe Peano
Giuseppe Peano was an Italian mathematician, whose work was of philosophical value. The author of over 200 books and papers, he was a founder of mathematical logic and set theory, to which he contributed much notation. The standard axiomatization of the natural numbers is named the Peano axioms in...
proposed axioms for arithmetic based on his axioms for natural numbers. Peano arithmetic has two axioms for multiplication:


Here S(y) represents the successor
Successor ordinal
In set theory, the successor of an ordinal number α is the smallest ordinal number greater than α. An ordinal number that is a successor is called a successor ordinal...
of y, or the natural number which follows y. The various properties like associativity can be proved from these and the other axioms of Peano arithmetic including induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
. For instance S(0). denoted by 1, is a multiplicative identity because

The axioms for integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s typically define them as equivalence classes of ordered pairs of natural numbers. The model is based on treating (x,y) as equivalent to x−y when x and y are treated as integers. Thus both (0,1) and (1,2) are equivalent to −1. The multiplication axiom for integers defined this way is

The rule that −1 × −1 = 1 can then be deduced from

Multiplication is extended in a similar way to rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s and then to real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s.
Multiplication with set theory
It is possible, though difficult, to create a recursive definition of multiplication with set theory. Such a system usually relies on the Peano definition of multiplication.Cartesian product
The definition of multiplication as repeated additionAddition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
provides a way to arrive at a set-theoretic interpretation of multiplication of cardinal numbers. In the expression
if the n copies of a are to be combined in disjoint union then clearly they must be made disjoint; an obvious way to do this is to use either a or n as the indexing set for the other. Then, the members of
 are exactly those of the Cartesian product
are exactly those of the Cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
 . The properties of the multiplicative operation as applying to natural numbers then follow trivially from the corresponding properties of the Cartesian product.
. The properties of the multiplicative operation as applying to natural numbers then follow trivially from the corresponding properties of the Cartesian product.Multiplication in group theory
There are many sets that, under the operation of multiplication, satisfy the axioms that define groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
structure. These axioms are closure, associativity, and the inclusion of an identity element and inverses.
A simple example is the set of non-zero rational numbers. Here we have identity 1, as opposed to groups under addition where the identity is typically 0. Note that with the rationals, we must exclude zero because, under multiplication, it does not have an inverse: there is no rational number that can be multiplied by zero to result in 1. In this example we have an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, but that is not always the case.
To see this, look at the set of invertible square matrices of a given dimension, over a given field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. Now it is straightforward to verify closure, associativity, and inclusion of identity (the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
) and inverses. However, matrix multiplication is not commutative, therefore this group is nonabelian.
Another fact of note is that the integers under multiplication is not a group, even if we exclude zero. This is easily seen by the nonexistence of an inverse for all elements other than 1 and -1.
Multiplication in group theory is typically notated either by a dot, or by juxtaposition (the omission of an operation symbol between elements). So multiplying element a by element b could be notated a
 b or ab. When referring to a group via the indication of the set and operation, the dot is used, e.g. our first example could be indicated by
b or ab. When referring to a group via the indication of the set and operation, the dot is used, e.g. our first example could be indicated by 
Multiplication of different kinds of numbers
Numbers can count (3 apples), order (the 3rd apple), or measure (3.5 feet high); as the history of mathematics has progressed from counting on our fingers to modelling quantum mechanics, multiplication has been generalized to more complicated and abstract types of numbers, and to things that are not numbers (such as matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
) or do not look much like numbers (such as quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s).
Integers
 is the sum of M copies of N when N and M are positive whole numbers. This gives the number of things in an array N wide and M high. Generalization to negative numbers can be done by
is the sum of M copies of N when N and M are positive whole numbers. This gives the number of things in an array N wide and M high. Generalization to negative numbers can be done by  and
and  . The same sign rules apply to rational and real numbers.
. The same sign rules apply to rational and real numbers.Rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s
- Generalization to fractions
 is by multiplying the numerators and denominators respectively:
is by multiplying the numerators and denominators respectively:  . This gives the area of a rectangle
. This gives the area of a rectangle  high and
high and  wide, and is the same as the number of things in an array when the rational numbers happen to be whole numbers.
wide, and is the same as the number of things in an array when the rational numbers happen to be whole numbers.
Real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s
 is the limit of the products of the corresponding terms in certain sequences of rationals that converge to x and y, respectively, and is significant in calculus
is the limit of the products of the corresponding terms in certain sequences of rationals that converge to x and y, respectively, and is significant in calculusCalculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
. This gives the area of a rectangle x high and y wide. See Products of sequences, above.
Complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s
- Considering complex numbers
 and
and  as ordered pairs of real numbers
as ordered pairs of real numbers  and
and  , the product
, the product  is
is  . This is the same as for reals,
. This is the same as for reals,  , when the imaginary parts
, when the imaginary parts  and
and  are zero.
are zero.
Further generalizations
- See Multiplication in group theory, above, and Multiplicative GroupMultiplicative groupIn mathematics and group theory the term multiplicative group refers to one of the following concepts, depending on the context*any group \scriptstyle\mathfrak \,\! whose binary operation is written in multiplicative notation ,*the underlying group under multiplication of the invertible elements of...
, which for example includes matrix multiplication. A very general, and abstract, concept of multiplication is as the "multiplicatively denoted" (second) binary operation in a ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
. An example of a ring which is not any of the above number systems is a polynomial ringPolynomial ringIn mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
(you can add and multiply polynomials, but polynomials are not numbers in any usual sense.)
Division
- Often division,
 , is the same as multiplication by an inverse,
, is the same as multiplication by an inverse,  . Multiplication for some types of "numbers" may have corresponding division, without inverses; in an integral domain x may have no inverse "
. Multiplication for some types of "numbers" may have corresponding division, without inverses; in an integral domain x may have no inverse " " but
" but  may be defined. In a division ringDivision ringIn abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
may be defined. In a division ringDivision ringIn abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
there are inverses but they are not commutative (since is not the same as
is not the same as  ,
,  may be ambiguous).
may be ambiguous).
Exponentiation
When multiplication is repeated, the resulting operation is known as exponentiation. For instance, the product of three factors of two (2×2×2) is "two raised to the third power", and is denoted by 23, a two with a superscript three. In this example, the number two is the base, and three is the exponent. In general, the exponent (or superscript) indicates how many times to multiply base by itself, so that the expression
indicates that the base a to be multiplied by itself n times.
See also
- Dimensional analysisDimensional analysisIn physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
- Multiplication algorithmMultiplication algorithmA multiplication algorithm is an algorithm to multiply two numbers. Depending on the size of the numbers, different algorithms are in use...
- Karatsuba algorithm, for large numbers
- Toom–Cook multiplication, for very large numbers
- Schönhage–Strassen algorithm, for huge numbers
- Multiplication tableMultiplication tableIn mathematics, a multiplication table is a mathematical table used to define a multiplication operation for an algebraic system....
- Multiplication ALU, how computers multiply
- Booth's multiplication algorithmBooth's multiplication algorithmBooth's multiplication algorithm is a multiplication algorithm that multiplies two signed binary numbers in two's complement notation. The algorithm was invented by Andrew Donald Booth in 1950 while doing research on crystallography at Birkbeck College in Bloomsbury, London...
- Floating pointFloating pointIn computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
- Fused multiply–add
- Multiply–accumulate
- Wallace treeWallace treeA Wallace tree is an efficient hardware implementation of a digital circuit that multiplies two integers, devised by an Australian Computer Scientist Chris Wallace in 1964.The Wallace tree has three steps:...
- Booth's multiplication algorithm
- Multiplicative inverseMultiplicative inverseIn mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
, reciprocal - FactorialFactorialIn mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
- Genaille–Lucas rulers
- Napier's bonesNapier's bonesNapier's bones is an abacus created by John Napier for calculation of products and quotients of numbers that was based on Arab mathematics and lattice multiplication used by Matrakci Nasuh in the Umdet-ul Hisab and Fibonacci writing in the Liber Abaci. Also called Rabdology...
- Peasant multiplication
- Product (mathematics)Product (mathematics)In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
, for generalizations - Slide ruleSlide ruleThe slide rule, also known colloquially as a slipstick, is a mechanical analog computer. The slide rule is used primarily for multiplication and division, and also for functions such as roots, logarithms and trigonometry, but is not normally used for addition or subtraction.Slide rules come in a...
External links
- Multiplication and Arithmetic Operations In Various Number Systems at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Modern Chinese Multiplication Techniques on an Abacus











