Real number - AbsoluteAstronomy.com

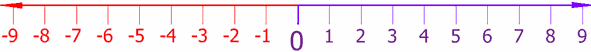
Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a real number is a value that represents a quantity along a continuum, such as -5 (an integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

), 4/3 (a rational number

Rational number

In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...

that is not an integer), 8.6 (a rational number given by a finite decimal representation), √2 (the square root of two, an algebraic number

Algebraic number

In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...

that is not rational) and π

' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...

(3.1415926535..., a transcendental number

Transcendental number

In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...

). Real numbers can be thought of as points on an infinitely long line

Line (geometry)

The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...

called the number line

Number line

In basic mathematics, a number line is a picture of a straight line on which every point is assumed to correspond to a real number and every real number to a point. Often the integers are shown as specially-marked points evenly spaced on the line...

or real line

Real line

In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...

, where the points corresponding to integers are equally spaced. Any real number can be determined by a possibly infinite decimal representation (such as that of π

above), where each consecutive digit a_r at rank r indicates the addition of a_r 10^-r to the decimal truncated at rank r-1. The real line

Real line

can be thought of as a part of the complex plane

Complex plane

In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...

, and correspondingly, complex number

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

s include real numbers as a special case.

These descriptions of the real numbers are not sufficiently rigorous by the modern standards of pure mathematics. The discovery of a suitably rigorous definition of the real numbers — indeed, the realization that a better definition was needed — was one of the most important developments of 19th century mathematics. The currently standard axiomatic definition is that real numbers form the unique complete

Complete space

In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....

totally ordered

Total order

In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...

field

Field (mathematics)

In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...

up to

Up to

In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...

isomorphism

Isomorphism

In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...

, whereas popular constructive definitions of real numbers include declaring them as equivalence classes of Cauchy sequence

Cauchy sequence

In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...

s of rational numbers, Dedekind cut

Dedekind cut

In mathematics, a Dedekind cut, named after Richard Dedekind, is a partition of the rationals into two non-empty parts A and B, such that all elements of A are less than all elements of B, and A contains no greatest element....

s, or certain infinite "decimal representations", together with precise interpretations for the arithmetic operations and the order relation. These definitions are equivalent in the realm of classical mathematics

Classical mathematics

In the foundations of mathematics, classical mathematics refers generally to the mainstream approach to mathematics, which is based on classical logic and ZFC set theory. It stands in contrast to other types of mathematics such as constructive mathematics or predicative mathematics; theories other...

Basic properties

A real number may be either rational

Rational number

or irrational

Irrational number

In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....

; either algebraic

Algebraic number

or transcendental

Transcendental number

; and either positive, negative, or zero

0 (number)

0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...

.
Real numbers are used to measure continuous

Continuous function

In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...

quantities. They may in theory be expressed by decimal representations that have an infinite sequence of digits to the right of the decimal point; these are often represented in the same form as 324.823122147… The ellipsis (three dots) indicate that there would still be more digits to come.

More formally, real numbers have the two basic properties of being an ordered field

Ordered field

In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...

, and having the least upper bound

Least upper bound axiom

The least upper bound axiom, also abbreviated as the LUB axiom, is an axiom of real analysis stating that the set R of real numbers has the least-upper-bound property. That is, if a nonempty set of real numbers has an upper bound, then it has a least upper bound...

property. The first says that real numbers comprise a field

Field (mathematics)

, with addition and multiplication as well as division by nonzero numbers, which can be totally ordered

Total order

In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...

on a number line in a way compatible with addition and multiplication. The second says that if a nonempty set of real numbers has an upper bound, then it has a least upper bound

Supremum

In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...

. The second condition distinguishes the real numbers from the rational numbers: for example, the set of rational numbers whose square is less than 2 is a set with an upper bound (e.g. 1.5) but no least upper bound: hence the rational numbers do not satisfy the least upper bound property.

In physics

In the physical sciences, most physical constants such as the universal gravitational constant, and physical variables, such as position, mass, speed, and electric charge, are modeled using real numbers. In fact, the fundamental physical theories such as classical mechanics

Classical mechanics

In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...

, electromagnetism

Electromagnetism

Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...

, quantum mechanics

Quantum mechanics

Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...

, general relativity

General relativity

General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...

and the standard model

Standard Model

The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...

are described using mathematical structures, typically smooth manifolds or Hilbert spaces, that are based on the real numbers although actual measurements of physical quantities are of finite accuracy and precision

Accuracy and precision

In the fields of science, engineering, industry and statistics, the accuracy of a measurement system is the degree of closeness of measurements of a quantity to that quantity's actual value. The precision of a measurement system, also called reproducibility or repeatability, is the degree to which...

.

In some recent developments of theoretical physics stemming from the holographic principle

Holographic principle

The holographic principle is a property of quantum gravity and string theories which states that the description of a volume of space can be thought of as encoded on a boundary to the region—preferably a light-like boundary like a gravitational horizon...

, the Universe is seen fundamentally as an information store, essentially zeroes and ones, organized in much less geometrical fashion and manifesting itself as space-time and particle fields only on a more superficial level. This approach removes the real number system from its foundational role in physics and even prohibits the existence of infinite precision real numbers in the physical universe by considerations based on the Bekenstein bound

Bekenstein bound

In physics, the Bekenstein bound is an upper limit on the entropy S, or information I, that can be contained within a given finite region of space which has a finite amount of energy—or conversely, the maximum amount of information required to perfectly describe a given physical system down to the...

In computation

Computer arithmetic cannot directly operate on real numbers, but only on a finite subset of rational numbers, limited by the number of bits used to store them, whether as floating-point numbers or arbitrary precision numbers. However, computer algebra system

Computer algebra system

A computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...

s can operate on irrational quantities

Irrational number

In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....

exactly by manipulating formulas for them (such as

, or

) rather than their rational or decimal approximation; however, it is not in general possible to determine whether two such expressions are equal (the Constant problem

Constant problem

In mathematics, the constant problem is the problem of deciding if a given expression is equal to zero.-The problem:This problem is also referred to as the identity problem or the method of zero estimates. It has no formal statement as such but refers to a general problem prevalent in...

).

A real number is said to be computable
Computable number
In mathematics, particularly theoretical computer science and mathematical logic, the computable numbers, also known as the recursive numbers or the computable reals, are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm...

if there exists an algorithm that yields its digits. Because there are only countably many algorithms, but an uncountable number of reals, almost all

Almost all

In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....

real numbers fail to be computable. Some constructivists

Constructivism (mathematics)

In the philosophy of mathematics, constructivism asserts that it is necessary to find a mathematical object to prove that it exists. When one assumes that an object does not exist and derives a contradiction from that assumption, one still has not found the object and therefore not proved its...

accept the existence of only those reals that are computable. The set of definable number

Definable number

A real number a is first-order definable in the language of set theory, without parameters, if there is a formula φ in the language of set theory, with one free variable, such that a is the unique real number such that φ holds in the standard model of set theory .For the purposes of this article,...

s is broader, but still only countable. If computers could use unlimited-precision real numbers (real computation

Real computation

In computability theory, the theory of real computation deals with hypothetical computing machines using infinite-precision real numbers. They are given this name because they operate on the set of real numbers...

), then one could solve NP-complete

NP-complete

In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...

problems, and even #P-complete problems in polynomial time, answering affirmatively the P = NP problem.

Notation

Mathematicians use the symbol R (or alternatively,

, the letter "R

R is the eighteenth letter of the basic modern Latin alphabet.-History:The original Semitic letter may have been inspired by an Egyptian hieroglyph for tp, "head". It was used for by Semites because in their language, the word for "head" was rêš . It developed into Greek Ρ and Latin R...

" in blackboard bold

Blackboard bold

Blackboard bold is a typeface style that is often used for certain symbols in mathematical texts, in which certain lines of the symbol are doubled. The symbols usually denote number sets...

, Unicode ℝ – U+211D) to represent the set of all real numbers (as this set is naturally endowed with a structure of field

Field (mathematics)

, the expression field of the real numbers is more frequently used than set of all real numbers). The notation Rⁿ refers to the Cartesian product

Cartesian product

In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...

of n copies of R, which is an n-dimension

Dimension

In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...

al vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

over the field of the real numbers; this vector space may be identified to the n-dimension

Dimension

al space of Euclidean geometry

Euclidean geometry

Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...

as soon as a coordinate system

Coordinate system

In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...

has been chosen in the latter. For example, a value from R³ consists of three real numbers and specifies the coordinates of a point

Point (geometry)

In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...

in 3-dimensional space.

In mathematics, real is used as an adjective, meaning that the underlying field is the field of the real numbers (or the real field). For example real matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

, real polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...

and real Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...

. As a substantive, the term is used almost strictly in reference to the real numbers themselves (e.g., The "set of all reals").

History

Vulgar fractions had been used by the Egyptians

History of Egypt

Egyptian history can be roughly divided into the following periods:*Prehistoric Egypt*Ancient Egypt**Early Dynastic Period of Egypt: 31st to 27th centuries BC**Old Kingdom of Egypt: 27th to 22nd centuries BC...

around 1000 BC; the Vedic "Sulba Sutras

Sulba Sutras

The Shulba Sutras or Śulbasūtras are sutra texts belonging to the Śrauta ritual and containing geometry related to fire-altar construction.- Purpose and origins :...

" ("The rules of chords") in, ca. 600 BC, include what may be the first 'use' of irrational number

Irrational number

In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....

s. The concept of irrationality was implicitly accepted by early Indian mathematicians

Indian mathematics

Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...

since Manava

Manava

Manava is an author of the Indian geometric text of Sulba Sutras.The Manava Sulbasutra is not the oldest , nor is it one of the most important, there being at least three Sulbasutras which are considered more important...

(c. 750–690 BC), who were aware that the square root

Square root

In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...

s of certain numbers such as 2 and 61 could not be exactly determined. Around 500 BC, the Greek mathematicians

Greek mathematics

Greek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...

led by Pythagoras

Pythagoras

Pythagoras of Samos was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him...

realized the need for irrational numbers, in particular the irrationality of the square root of 2

Square root of 2

The square root of 2, often known as root 2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.Geometrically the square root of 2 is the...

.

The Middle Ages

Middle Ages

The Middle Ages is a periodization of European history from the 5th century to the 15th century. The Middle Ages follows the fall of the Western Roman Empire in 476 and precedes the Early Modern Era. It is the middle period of a three-period division of Western history: Classic, Medieval and Modern...

saw the acceptance of zero, negative, integral

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

and fractional

Fraction (mathematics)

A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...

numbers, first by Indian and Chinese mathematicians

Chinese mathematics

Mathematics in China emerged independently by the 11th century BC. The Chinese independently developed very large and negative numbers, decimals, a place value decimal system, a binary system, algebra, geometry, and trigonometry....

, and then by Arabic mathematicians, who were also the first to treat irrational numbers as algebraic objects, which was made possible by the development of algebra

Algebra

Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...

. Arabic mathematicians merged the concepts of "number

Number

A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....

" and "magnitude

Magnitude (mathematics)

The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....

" into a more general idea of real numbers. The Egypt

Egypt

Egypt , officially the Arab Republic of Egypt, Arabic: , is a country mainly in North Africa, with the Sinai Peninsula forming a land bridge in Southwest Asia. Egypt is thus a transcontinental country, and a major power in Africa, the Mediterranean Basin, the Middle East and the Muslim world...

ian mathematician Abū Kāmil Shujā ibn Aslam (c. 850–930) was the first to accept irrational numbers as solutions to quadratic equation

Quadratic equation

In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...

s or as coefficient

Coefficient

In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...

s in an equation

Equation

An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...

, often in the form of square roots, cube roots and fourth roots

Nth root

In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...

.

In the 16th century, Simon Stevin

Simon Stevin

Simon Stevin was a Flemish mathematician and military engineer. He was active in a great many areas of science and engineering, both theoretical and practical...

created the basis for modern decimal

Decimal

The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....

notation, and insisted that there is no difference between rational and irrational numbers in this regard.

In the 17th century, Descartes introduced the term "real" to describe roots of a polynomial, distinguishing them from "imaginary" ones.

In the 18th and 19th centuries there was much work on irrational and transcendental number

Transcendental number

s. Johann Heinrich Lambert

Johann Heinrich Lambert

Johann Heinrich Lambert was a Swiss mathematician, physicist, philosopher and astronomer.Asteroid 187 Lamberta was named in his honour.-Biography:...

(1761) gave the first flawed proof that π cannot be rational; Adrien-Marie Legendre

Adrien-Marie Legendre

Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...

(1794) completed the proof, and showed that π is not the square root of a rational number. Paolo Ruffini

Paolo Ruffini

Paolo Ruffini was an Italian mathematician and philosopher.By 1788 he had earned university degrees in philosophy, medicine/surgery, and mathematics...

(1799) and Niels Henrik Abel

Niels Henrik Abel

Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...

(1842) both constructed proofs of Abel–Ruffini theorem

Abel–Ruffini theorem

In algebra, the Abel–Ruffini theorem states that there is no general algebraic solution—that is, solution in radicals— to polynomial equations of degree five or higher.- Interpretation :...

: that the general quintic

Quintic equation

In mathematics, a quintic function is a function of the formg=ax^5+bx^4+cx^3+dx^2+ex+f,\,where a, b, c, d, e and f are members of a field, typically the rational numbers, the real numbers or the complex numbers, and a is nonzero...

or higher equations cannot be solved by a general formula involving only arithmetical operations and roots.

Évariste Galois

Évariste Galois

Évariste Galois was a French mathematician born in Bourg-la-Reine. While still in his teens, he was able to determine a necessary and sufficient condition for a polynomial to be solvable by radicals, thereby solving a long-standing problem...

(1832) developed techniques for determining whether a given equation could be solved by radicals, which gave rise to the field of Galois theory

Galois theory

In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...

. Joseph Liouville

Joseph Liouville

- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...

(1840) showed that neither e nor e² can be a root of an integer quadratic equation

Quadratic equation

In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...

, and then established existence of transcendental numbers, the proof being subsequently displaced by Georg Cantor (1873). Charles Hermite

Charles Hermite

Charles Hermite was a French mathematician who did research on number theory, quadratic forms, invariant theory, orthogonal polynomials, elliptic functions, and algebra....

(1873) first proved that e

E (mathematical constant)

The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...

is transcendental, and Ferdinand von Lindemann

Ferdinand von Lindemann

Carl Louis Ferdinand von Lindemann was a German mathematician, noted for his proof, published in 1882, that π is a transcendental number, i.e., it is not a root of any polynomial with rational coefficients....

(1882), showed that π is transcendental. Lindemann's proof was much simplified by Weierstrass (1885), still further by David Hilbert

David Hilbert

David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...

(1893), and has finally been made elementary by Adolf Hurwitz

Adolf Hurwitz

Adolf Hurwitz was a German mathematician.-Early life:He was born to a Jewish family in Hildesheim, former Kingdom of Hannover, now Lower Saxony, Germany, and died in Zürich, in Switzerland. Family records indicate that he had siblings and cousins, but their names have yet to be confirmed...

and Paul Gordan.

The development of calculus

Calculus

Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...

in the 18th century used the entire set of real numbers without having defined them cleanly. The first rigorous definition was given by Georg Cantor

Georg Cantor

Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...

in 1871. In 1874 he showed that the set of all real numbers is uncountably infinite but the set of all algebraic number

Algebraic number

s is countably infinite. Contrary to widely held beliefs, his first method was not his famous diagonal argument

Cantor's diagonal argument

Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural...

, which he published in 1891. See Cantor's first uncountability proof

Cantor's first uncountability proof

Georg Cantor's first uncountability proof demonstrates that the set of all real numbers is uncountable. This proof differs from the more familiar proof that uses his diagonal argument...

Definition

The real number system

can be defined axiomatically

Axiomatic system

In mathematics, an axiomatic system is any set of axioms from which some or all axioms can be used in conjunction to logically derive theorems. A mathematical theory consists of an axiomatic system and all its derived theorems...

up to an isomorphism

Isomorphism

, which is described below. There are also many ways to construct "the" real number system, for example, starting from natural numbers, then defining rational numbers algebraically, and finally defining real numbers as equivalence classes of their Cauchy sequence

Cauchy sequence

In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...

s or as Dedekind cut

Dedekind cut

s, which are certain subsets of rational numbers. Another possibility is to start from some rigorous axiomatization of Euclidean geometry (Hilbert, Tarski etc.) and then define the real number system geometrically. From the structuralist

Structuralism (philosophy of mathematics)

Structuralism is a theory in the philosophy of mathematics that holds that mathematical theories describe structures, and that mathematical objects are exhaustively defined by their place in such structures, consequently having no intrinsic properties. For instance, it would maintain that all that...

point of view all these constructions are on equal footing.

Axiomatic approach

Let R denote the set of all real numbers. Then:

The set R is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...

, meaning that addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....

and multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....

are defined and have the usual properties.
The field R is ordered
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...

, meaning that there is a total order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...

≥ such that, for all real numbers x, y and z:
- if x ≥ y then x + z ≥ y + z;
- if x ≥ 0 and y ≥ 0 then xy ≥ 0.
The order is Dedekind-complete; that is, every non-empty
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...

subset S of R with an upper bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...

in R has a least upper bound
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...

(also called supremum) in R.

The last property is what differentiates the reals from the rationals

Rational number

. For example, the set of rationals with square less than 2 has a rational upper bound (e.g., 1.5) but no rational least upper bound, because the square root

Square root

In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...

of 2 is not rational.

The real numbers are uniquely specified by the above properties. More precisely, given any two Dedekind-complete ordered fields R₁ and R₂, there exists a unique field isomorphism

Isomorphism

from R₁ to R₂, allowing us to think of them as essentially the same mathematical object.

For another axiomatization of R, see Tarski's axiomatization of the reals

Tarski's axiomatization of the reals

In 1936, Alfred Tarski set out an axiomatization of the real numbers and their arithmetic, consisting of only the 8 axioms shown below and a mere four primitive notions: the set of reals denoted R, a binary total order over R, denoted by infix...

Construction from the rational numbers

The real numbers can be constructed as a completion of the rational numbers in such a way that a sequence defined by a decimal or binary expansion like {3, 3.1, 3.14, 3.141, 3.1415,...} converges

Limit of a sequence

The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...

to a unique real number. For details and other constructions of real numbers, see construction of the real numbers.

Completeness

A main reason for using real numbers is that the reals contain all limits

Limit (mathematics)

In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...

. More precisely, every sequence of real numbers having the property that consecutive terms of the sequence become arbitrarily close to each other necessarily has the property that after some term in the sequence the remaining terms are arbitrarily close to some specific real number. In mathematical terminology, this means that the reals are complete (in the sense of metric space

Metric space

In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...

s or uniform space

Uniform space

In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...

s, which is a different sense than the Dedekind completeness of the order in the previous section). This is formally defined in the following way:

A sequence

Sequence

In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...

(x_n) of real numbers is called a Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...

if for any ε > 0 there exists an integer N (possibly depending on ε) such that the distance

Distance

Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...

|x_n − x_m| is less than ε for all n and m that are both greater than N. In other words, a sequence is a Cauchy

Augustin Louis Cauchy

Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...

sequence if its elements x_n eventually come and remain arbitrarily close to each other.

A sequence (x_n) converges to the limit x if for any ε > 0 there exists an integer N (possibly depending on ε) such that the distance |x_n − x| is less than ε provided that n is greater than N. In other words, a sequence has limit x if its elements eventually come and remain arbitrarily close to x.

Notice that every convergent sequence is a Cauchy sequence. An important fact about the real numbers is that the converse is also true:

Every Cauchy sequence of real numbers is convergent to a real number.

That is, the reals are complete.

Note that the rationals are not complete. For example, the sequence (1, 1.4, 1.41, 1.414, 1.4142, 1.41421, ...), where each term adds a digit of the decimal expansion of the positive square root

Square root

In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...

of 2, is Cauchy but it does not converge to a rational number. (In the real numbers, in contrast, it converges to the positive square root

Square root

In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...

of 2.)

The existence of limits of Cauchy sequences is what makes calculus

Calculus

work and is of great practical use. The standard numerical test to determine if a sequence has a limit is to test if it is a Cauchy sequence, as the limit is typically not known in advance.

For example, the standard series of the exponential function

Exponential function

In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...

converges to a real number because for every x the sums

can be made arbitrarily small by choosing N sufficiently large. This proves that the sequence is Cauchy, so we know that the sequence converges even if the limit is not known in advance.

"The complete ordered field"

The real numbers are often described as "the complete ordered field", a phrase that can be interpreted in several ways.

First, an order can be lattice-complete

Complete lattice

In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...

. It is easy to see that no ordered field can be lattice-complete, because it can have no largest element (given any element z, z + 1 is larger), so this is not the sense that is meant.

Additionally, an order can be Dedekind-complete, as defined in the section Axioms. The uniqueness result at the end of that section justifies using the word "the" in the phrase "complete ordered field" when this is the sense of "complete" that is meant. This sense of completeness is most closely related to the construction of the reals from Dedekind cuts, since that construction starts from an ordered field (the rationals) and then forms the Dedekind-completion of it in a standard way.

These two notions of completeness ignore the field structure. However, an ordered group

Ordered group

In abstract algebra, a partially-ordered group is a group equipped with a partial order "≤" that is translation-invariant; in other words, "≤" has the property that, for all a, b, and g in G, if a ≤ b then a+g ≤ b+g and g+a ≤ g+b.An element x of G is called positive element if 0 ≤ x...

(in this case, the additive group of the field) defines a uniform

Uniform space

structure, and uniform structures have a notion of completeness (topology); the description in the section Completeness above is a special case. (We refer to the notion of completeness in uniform spaces rather than the related and better known notion for metric space

Metric space

s, since the definition of metric space relies on already having a characterisation of the real numbers.) It is not true that R is the only uniformly complete ordered field, but it is the only uniformly complete Archimedean field, and indeed one often hears the phrase "complete Archimedean field" instead of "complete ordered field". Since it can be proved that any uniformly complete Archimedean field must also be Dedekind-complete (and vice versa, of course), this justifies using "the" in the phrase "the complete Archimedean field". This sense of completeness is most closely related to the construction of the reals from Cauchy sequences (the construction carried out in full in this article), since it starts with an Archimedean field (the rationals) and forms the uniform completion of it in a standard way.

But the original use of the phrase "complete Archimedean field" was by David Hilbert

David Hilbert

, who meant still something else by it. He meant that the real numbers form the largest Archimedean field in the sense that every other Archimedean field is a subfield of R. Thus R is "complete" in the sense that nothing further can be added to it without making it no longer an Archimedean field. This sense of completeness is most closely related to the construction of the reals from surreal number

Surreal number

In mathematics, the surreal number system is an arithmetic continuum containing the real numbers as well as infinite and infinitesimal numbers, respectively larger or smaller in absolute value than any positive real number...

s, since that construction starts with a proper class that contains every ordered field (the surreals) and then selects from it the largest Archimedean subfield.

Advanced properties

The reals are uncountable; that is, there are strictly more real numbers than natural number

Natural number

In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...

s, even though both sets are infinite. In fact, the cardinality of the reals

Cardinality of the continuum

In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....

equals that of the set of subsets (i.e., the power set) of the natural numbers, and Cantor's diagonal argument

Cantor's diagonal argument

states that the latter set's cardinality is strictly bigger than the cardinality of N. Since only a countable set of real numbers can be algebraic

Algebraic number

, almost all

Almost all

In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....

real numbers are transcendental

Transcendental number

. The non-existence of a subset of the reals with cardinality strictly between that of the integers and the reals is known as the continuum hypothesis

Continuum hypothesis

In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...

. The continuum hypothesis can neither be proved nor be disproved; it is independent from the axioms of set theory.

The real numbers form a metric space

Metric space

: the distance between x and y is defined to be the absolute value

Absolute value

In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...

|x − y|. By virtue of being a totally ordered

Total order

In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...

set, they also carry an order topology

Order topology

In mathematics, an order topology is a certain topology that can be defined on any totally ordered set. It is a natural generalization of the topology of the real numbers to arbitrary totally ordered sets...

; the topology

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

arising from the metric and the one arising from the order are identical, but yield different presentations for the topology – in the order topology as intervals, in the metric topology as epsilon-balls. The Dedekind cuts construction uses the order topology presentation, while the Cauchy sequences construction uses the metric topology presentation. The reals are a contractible (hence connected

Connected space

In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...

and simply connected), separable metric space of dimension

Dimension

1, and are everywhere dense. The real numbers are locally compact but not compact

Compact space

In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...

. There are various properties that uniquely specify them; for instance, all unbounded, connected, and separable order topologies

Total order

In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...

are necessarily homeomorphic to the reals.

Every nonnegative real number has a square root

Square root

In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...

in R, although no negative number does. This shows that the order on R is determined by its algebraic structure. Also, every polynomial of odd degree admits at least one real root: these two properties make R the premier example of a real closed field

Real closed field

In mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...

. Proving this is the first half of one proof of the fundamental theorem of algebra

Fundamental theorem of algebra

The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...

.

The reals carry a canonical measure

Measure (mathematics)

In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...

, the Lebesgue measure

Lebesgue measure

In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...

, which is the Haar measure

Haar measure

In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....

on their structure as a topological group

Topological group

In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...

normalised such that the unit interval

Unit interval

In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...

[0,1] has measure 1.

The supremum axiom of the reals refers to subsets of the reals and is therefore a second-order logical statement. It is not possible to characterize the reals with first-order logic

First-order logic

First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...

alone: the Löwenheim–Skolem theorem implies that there exists a countable dense subset of the real numbers satisfying exactly the same sentences in first order logic as the real numbers themselves. The set of hyperreal number

Hyperreal number

The system of hyperreal numbers represents a rigorous method of treating the infinite and infinitesimal quantities. The hyperreals, or nonstandard reals, *R, are an extension of the real numbers R that contains numbers greater than anything of the form1 + 1 + \cdots + 1. \, Such a number is...

s satisfies the same first order sentences as R. Ordered fields that satisfy the same first-order sentences as R are called nonstandard models

Non-standard model

In model theory, a discipline within mathematical logic, a non-standard model is a model of a theory that is not isomorphic to the intended model . If the intended model is infinite and the language is first-order, then the Löwenheim-Skolem theorems guarantee the existence of non-standard models...

of R. This is what makes nonstandard analysis

Non-standard analysis

Non-standard analysis is a branch of mathematics that formulates analysis using a rigorous notion of an infinitesimal number.Non-standard analysis was introduced in the early 1960s by the mathematician Abraham Robinson. He wrote:...

work; by proving a first-order statement in some nonstandard model (which may be easier than proving it in R), we know that the same statement must also be true of R.

Generalizations and extensions

The real numbers can be generalized and extended in several different directions:

The complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

s contain solutions to all polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...

equations and hence are an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...

unlike the real numbers. However, the complex numbers are not an ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...

.
The affinely extended real number system adds two elements +∞ and −∞. It is a compact space
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...

. It is no longer a field, not even an additive group, but it still has a total order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...

; moreover, it is a complete lattice
Complete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...

.
The real projective line adds only one value ∞. It is also a compact space. Again, it is no longer a field, not even an additive group. However, it allows division of a non-zero element by zero. It is not ordered anymore.
The long real line
Long line (topology)
In topology, the long line is a topological space somewhat similar to the real line, but in a certain way "longer". It behaves locally just like the real line, but has different large-scale properties. Therefore it serves as one of the basic counterexamples of topology...

pastes together ℵ₁* + ℵ₁ copies of the real line plus a single point (here ℵ₁* denotes the reversed ordering of ℵ₁) to create an ordered set that is "locally" identical to the real numbers, but somehow longer; for instance, there is an order-preserving embedding of ℵ₁ in the long real line but not in the real numbers. The long real line is the largest ordered set that is complete and locally Archimedean. As with the previous two examples, this set is no longer a field or additive group.
Ordered fields extending the reals are the hyperreal number
Hyperreal number
The system of hyperreal numbers represents a rigorous method of treating the infinite and infinitesimal quantities. The hyperreals, or nonstandard reals, *R, are an extension of the real numbers R that contains numbers greater than anything of the form1 + 1 + \cdots + 1. \, Such a number is...

s and the surreal number
Surreal number
In mathematics, the surreal number system is an arithmetic continuum containing the real numbers as well as infinite and infinitesimal numbers, respectively larger or smaller in absolute value than any positive real number...

s; both of them contain infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...

and infinitely large numbers and thus are not Archimedean
Archimedean group
In abstract algebra, a branch of mathematics, an Archimedean group is an algebraic structure consisting of a set together with a binary operation and binary relation satisfying certain axioms detailed below. We can also say that an Archimedean group is a linearly ordered group for which the...

.
Self-adjoint operator
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...

s on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...

(for example, self-adjoint square complex matrices) generalize the reals in many respects: they can be ordered (though not totally ordered), they are complete, all their eigenvalues are real and they form a real associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...

. Positive-definite operators correspond to the positive reals and normal operator
Normal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....

s correspond to the complex numbers.

"Reals" in set theory

In set theory

Set theory

Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...

, specifically descriptive set theory

Descriptive set theory

In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...

, the Baire space

Baire space (set theory)

In set theory, the Baire space is the set of all infinite sequences of natural numbers with a certain topology. This space is commonly used in descriptive set theory, to the extent that its elements are often called “reals.” It is often denoted B, N'N, or ωω...

is used as a surrogate for the real numbers since the latter have some topological properties (connectedness) that are a technical inconvenience. Elements of Baire space are referred to as "reals".

Real numbers and logic

The real numbers are most often formalized using the Zermelo-Fraenkel axiomatization of set theory, but some mathematicians study the real numbers with other logical foundations of mathematics. In particular, the real numbers are also studied in reverse mathematics

Reverse mathematics

Reverse mathematics is a program in mathematical logic that seeks to determine which axioms are required to prove theorems of mathematics. Its defining method can briefly be described as "going backwards from the theorems to the axioms", in contrast to the ordinary mathematical practice of...

and in constructive mathematics

Constructivism (mathematics)

.

Abraham Robinson

Abraham Robinson

Abraham Robinson was a mathematician who is most widely known for development of non-standard analysis, a mathematically rigorous system whereby infinitesimal and infinite numbers were incorporated into mathematics....

's theory of nonstandard or hyperreal number

Hyperreal number

s extends the set of the real numbers by infinitesimal numbers, which allows to built infinitesimal calculus

Infinitesimal calculus

Infinitesimal calculus is the part of mathematics concerned with finding slope of curves, areas under curves, minima and maxima, and other geometric and analytic problems. It was independently developed by Gottfried Leibniz and Isaac Newton starting in the 1660s...

in a way which is closer to the usual intuition of the notion of limit

Limit (mathematics)

. Edward Nelson

Edward Nelson

Edward Nelson is a professor in the Mathematics Department at Princeton University. He is known for his work on mathematical physics and mathematical logic...

's internal set theory

Internal set theory

Internal set theory is a mathematical theory of sets developed by Edward Nelson that provides an axiomatic basis for a portion of the non-standard analysis introduced by Abraham Robinson. Instead of adding new elements to the real numbers, the axioms introduce a new term, "standard", which can be...

is a non Zermelo-Fraenkel set theory which allows to consider the non standard real numbers as elements of the set of the reals (and not of an extension of it as in Robinson's theory).

The continuum hypothesis

Continuum hypothesis

posits that the cardinality of the set of the real numbers is

, i.e. the smallest infinite cardinal number

Cardinal number

In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...

after

, the cardinality of the integers. Paul Cohen

Paul Cohen (mathematician)

Paul Joseph Cohen was an American mathematician best known for his proof of the independence of the continuum hypothesis and the axiom of choice from Zermelo–Fraenkel set theory, the most widely accepted axiomatization of set theory.-Early years:Cohen was born in Long Branch, New Jersey, into a...

has proved in 1963 that it is an axiom which is independent of the other axioms of set theory, that is one may choose either the continuum hypothesis or its negation as an axiom of set theory, without making it contradictory.

External links

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Basic properties

In physics

In computation

Notation

History

Definition

Axiomatic approach

Construction from the rational numbers

Completeness

"The complete ordered field"

Advanced properties

Generalizations and extensions

"Reals" in set theory

Real numbers and logic

See also

External links