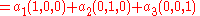Linear combination
Encyclopedia
In mathematics
, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results (e.g. a linear combination of x and y would be any expression of the form ax + by, where a and b are constants). The concept of linear combinations is central to linear algebra
and related fields of mathematics.
Most of this article deals with linear combinations in the context of a vector space
over a field
, with some generalizations given at the end of the article.
s and call elements of K scalars
.
If v1,...,vn are vectors and a1,...,an are scalars, then the linear combination of those vectors with those scalars as coefficients is
There is some ambiguity in the use of the term "linear combination" as to whether it refers to the expression or to its value. In most cases the value is emphasized, like in the assertion "the set of all linear combinations of v1,...,vn always forms a subspace"; however one could also say "two different linear combinations can have the same value" in which case the expression must have been meant. The subtle difference between these uses is the essence of the notion of linear dependence: a family F of vectors is linearly independent precisely if any linear combination of the vectors in F (as value) is uniquely so (as expression). In any case, even when viewed as expressions, all that matters about a linear combination is the coefficient of each vi; trivial modifications such as permuting the terms or adding terms with zero coefficient are not considered to give new linear combinations. Adding and subtracting isn't a real mathematical action.
In a given situation, K and V may be specified explicitly, or they may be obvious from context. In that case, we often speak of a linear combination of the vectors v1,...,vn, with the coefficients unspecified (except that they must belong to K). Or, if S is a subset
of V, we may speak of a linear combination of vectors in S, where both the coefficients and the vectors are unspecified, except that the vectors must belong to the set S (and the coefficients must belong to K). Finally, we may speak simply of a linear combination, where nothing is specified (except that the vectors must belong to V and the coefficients must belong to K); in this case one is probably referring to the expression, since every vector in V is certainly the value of some linear combination.
Note that by definition, a linear combination involves only finitely many vectors (except as described in Generalizations below).
However, the set S that the vectors are taken from (if one is mentioned) can still be infinite; each individual linear combination will only involve finitely many vectors.
Also, there is no reason that n cannot be zero
; in that case, we declare by convention that the result of the linear combination is the zero vector in V.
s, and let the vector space V be the Euclidean space
R3.
Consider the vectors e1 = (1,0,0), e2 = (0,1,0) and e3 = (0,0,1).
Then any vector in R3 is a linear combination of e1, e2 and e3.
To see that this is so, take an arbitrary vector (a1,a2,a3) in R3, and write:
Functions
Let K be the set C of all complex number
s, and let V be the set CC(R) of all continuous
function
s from the real line
R to the complex plane
C.
Consider the vectors (functions) f and g defined by f(t) := eit and g(t) := e−it.
(Here, e is the base of the natural logarithm
, about 2.71828..., and i is the imaginary unit
, a square root of −1.)
Some linear combinations of f and g are:
On the other hand, the constant function 3 is not a linear combination of f and g. To see this, suppose that 3 could be written as a linear combination of eit and e−it. This means that there would exist complex scalars a and b such that aeit + be−it = 3 for all real numbers t. Setting t = 0 and t = π gives the equations a + b = 3 and a + b = −3, and clearly this cannot happen. See Euler's identity.
s with coefficients taken from the field K.
Consider the vectors (polynomials) p1 := 1, p2 := x + 1, and p3 := x2 + x + 1.
Is the polynomial x2 − 1 a linear combination of p1, p2, and p3?
To find out, consider an arbitrary linear combination of these vectors and try to see when it equals the desired vector x2 − 1.
Picking arbitrary coefficients a1, a2, and a3, we want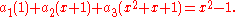
Multiplying the polynomials out, this means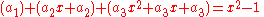
and collecting like powers of x, we get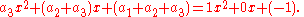
Two polynomials are equal if and only if
their corresponding coefficients are equal, so we can conclude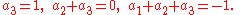
This system of linear equations can easily be solved.
First, the first equation simply says that a3 is 1.
Knowing that, we can solve the second equation for a2, which comes out to −1.
Finally, the last equation tells us that a1 is also −1.
Therefore, the only possible way to get a linear combination is with these coefficients.
Indeed,
so x2 − 1 is a linear combination of p1, p2, and p3.
On the other hand, what about the polynomial x3 − 1?
If we try to make this vector a linear combination of p1, p2, and p3, then following the same process as before, we’ll get the equation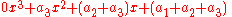

However, when we set corresponding coefficients equal in this case, the equation for x3 is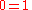
which is always false.
Therefore, there is no way for this to work, and x3 − 1 is not a linear combination of p1, p2, and p3.
Take an arbitrary field K, an arbitrary vector space V, and let v1,...,vn be vectors (in V).
It’s interesting to consider the set of all linear combinations of these vectors.
This set is called the linear span
(or just span) of the vectors, say S ={v1,...,vn}. We write the span of S as span(S) or sp(S):
a single vector can be written in two different ways as a linear combination of them:
Equivalently, by subtracting these (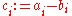 ) a non-trivial combination is zero:
) a non-trivial combination is zero:
If that is possible, then v1,...,vn are called linearly dependent; otherwise, they are linearly independent.
Similarly, we can speak of linear dependence or independence of an arbitrary set S of vectors.
If S is linearly independent and the span of S equals V, then S is a basis
for V.
, and convex combination
, and the associated notions of sets closed under these operations.
Because these are more restricted operations, more subsets will be closed under them, so affine subsets, convex cones, and convex sets are generalizations of vector subspaces: a vector subspace is also an affine subspace, a convex cone, and a convex set, but a convex set need not be a vector subspace, affine, or a convex cone.
These concepts often arise when one can take certain linear combinations of objects, but not any: for example, probability distribution
s are closed under convex combination (they form a convex set), but not conical or affine combinations (or linear), and positive measures are closed under conical combination but not affine or linear – hence one defines signed measure
s as the linear closure.
Linear and affine combinations can be defined over any field (or ring), but conical and convex combination require a notion of "positive", and hence can only be defined over an ordered field
(or ordered ring
), generally the real numbers.
If one allows only scalar multiplication, not addition, one obtains a (not necessarily convex) cone
; one often restricts the definition to only allowing multiplication by positive scalars.
All of these concepts are usually defined as subsets of an ambient vector space (except for affine spaces, which are also considered as "vector spaces forgetting the origin"), rather than being axiomatized independently.
, one can consider vector spaces to be algebras
over the operad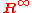 (the infinite direct sum
(the infinite direct sum
, so only finitely many terms are non-zero; this corresponds to only taking finite sums), which parametrizes linear combinations: the vector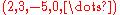 for instance corresponds to the linear combination
for instance corresponds to the linear combination 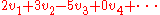 . Similarly, one can consider affine combinations, conical combinations, and convex combinations to correspond to the sub-operads where the terms sum to 1, the terms are all non-negative, or both, respectively. Graphically, these are the infinite affine hyperplane, the infinite hyper-octant, and the infinite simplex. This formalizes what is meant by
. Similarly, one can consider affine combinations, conical combinations, and convex combinations to correspond to the sub-operads where the terms sum to 1, the terms are all non-negative, or both, respectively. Graphically, these are the infinite affine hyperplane, the infinite hyper-octant, and the infinite simplex. This formalizes what is meant by  being or the standard simplex being model spaces, and such observations as that every bounded convex polytope
being or the standard simplex being model spaces, and such observations as that every bounded convex polytope
is the image of a simplex. Here suboperads correspond to more restricted operations and thus more general theories.
From this point of view, we can think of linear combinations as the most general sort of operation on a vector space – saying that a vector space is an algebra over the operad of linear combinations is precisely the statement that all possible algebraic operations in a vector space are linear combinations.
The basic operations of addition and scalar multiplication, together with the existence of an additive identity and additive inverses, cannot be combined in any more complicated way than the generic linear combination: the basic operations are a generating set
for the operad of all linear combinations.
Ultimately, this fact lies at the heart of the usefulness of linear combinations in the study of vector spaces.
, then there may be a way to make sense of certain infinite linear combinations, using the topology of V.
For example, we might be able to speak of a1v1 + a2v2 + a3v3 + ..., going on forever.
Such infinite linear combinations do not always make sense; we call them convergent when they do.
Allowing more linear combinations in this case can also lead to a different concept of span, linear independence, and basis.
The articles on the various flavours of topological vector spaces go into more detail about these.
If K is a commutative ring
instead of a field, then everything that has been said above about linear combinations generalizes to this case without change.
The only difference is that we call spaces like V modules
instead of vector spaces.
If K is a noncommutative ring, then the concept still generalizes, with one caveat:
Since modules over noncommutative rings come in left and right versions, our linear combinations may also come in either of these versions, whatever is appropriate for the given module.
This is simply a matter of doing scalar multiplication on the correct side.
A more complicated twist comes when V is a bimodule
over two rings, KL and KR.
In that case, the most general linear combination looks like
where a1,...,an belong to KL, b1,...,bn belong to KR, and v1,...,vn belong to V.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results (e.g. a linear combination of x and y would be any expression of the form ax + by, where a and b are constants). The concept of linear combinations is central to linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
and related fields of mathematics.
Most of this article deals with linear combinations in the context of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, with some generalizations given at the end of the article.
Definition
Suppose that K is a field (for example, the real numbers) and V is a vector space over K. As usual, we call elements of V vectorVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s and call elements of K scalars
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
.
If v1,...,vn are vectors and a1,...,an are scalars, then the linear combination of those vectors with those scalars as coefficients is

There is some ambiguity in the use of the term "linear combination" as to whether it refers to the expression or to its value. In most cases the value is emphasized, like in the assertion "the set of all linear combinations of v1,...,vn always forms a subspace"; however one could also say "two different linear combinations can have the same value" in which case the expression must have been meant. The subtle difference between these uses is the essence of the notion of linear dependence: a family F of vectors is linearly independent precisely if any linear combination of the vectors in F (as value) is uniquely so (as expression). In any case, even when viewed as expressions, all that matters about a linear combination is the coefficient of each vi; trivial modifications such as permuting the terms or adding terms with zero coefficient are not considered to give new linear combinations. Adding and subtracting isn't a real mathematical action.
In a given situation, K and V may be specified explicitly, or they may be obvious from context. In that case, we often speak of a linear combination of the vectors v1,...,vn, with the coefficients unspecified (except that they must belong to K). Or, if S is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of V, we may speak of a linear combination of vectors in S, where both the coefficients and the vectors are unspecified, except that the vectors must belong to the set S (and the coefficients must belong to K). Finally, we may speak simply of a linear combination, where nothing is specified (except that the vectors must belong to V and the coefficients must belong to K); in this case one is probably referring to the expression, since every vector in V is certainly the value of some linear combination.
Note that by definition, a linear combination involves only finitely many vectors (except as described in Generalizations below).
However, the set S that the vectors are taken from (if one is mentioned) can still be infinite; each individual linear combination will only involve finitely many vectors.
Also, there is no reason that n cannot be zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
; in that case, we declare by convention that the result of the linear combination is the zero vector in V.
Vectors
Let the field K be the set R of real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, and let the vector space V be the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
R3.
Consider the vectors e1 = (1,0,0), e2 = (0,1,0) and e3 = (0,0,1).
Then any vector in R3 is a linear combination of e1, e2 and e3.
To see that this is so, take an arbitrary vector (a1,a2,a3) in R3, and write:

FunctionsFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
Let K be the set C of all complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, and let V be the set CC(R) of all continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s from the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
R to the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
C.
Consider the vectors (functions) f and g defined by f(t) := eit and g(t) := e−it.
(Here, e is the base of the natural logarithm
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
, about 2.71828..., and i is the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
, a square root of −1.)
Some linear combinations of f and g are:
On the other hand, the constant function 3 is not a linear combination of f and g. To see this, suppose that 3 could be written as a linear combination of eit and e−it. This means that there would exist complex scalars a and b such that aeit + be−it = 3 for all real numbers t. Setting t = 0 and t = π gives the equations a + b = 3 and a + b = −3, and clearly this cannot happen. See Euler's identity.
Polynomials
Let K be R, C, or any field, and let V be the set P of all polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s with coefficients taken from the field K.
Consider the vectors (polynomials) p1 := 1, p2 := x + 1, and p3 := x2 + x + 1.
Is the polynomial x2 − 1 a linear combination of p1, p2, and p3?
To find out, consider an arbitrary linear combination of these vectors and try to see when it equals the desired vector x2 − 1.
Picking arbitrary coefficients a1, a2, and a3, we want
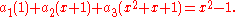
Multiplying the polynomials out, this means
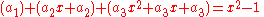
and collecting like powers of x, we get
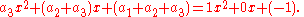
Two polynomials are equal if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
their corresponding coefficients are equal, so we can conclude
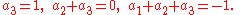
This system of linear equations can easily be solved.
First, the first equation simply says that a3 is 1.
Knowing that, we can solve the second equation for a2, which comes out to −1.
Finally, the last equation tells us that a1 is also −1.
Therefore, the only possible way to get a linear combination is with these coefficients.
Indeed,

so x2 − 1 is a linear combination of p1, p2, and p3.
On the other hand, what about the polynomial x3 − 1?
If we try to make this vector a linear combination of p1, p2, and p3, then following the same process as before, we’ll get the equation
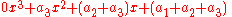

However, when we set corresponding coefficients equal in this case, the equation for x3 is
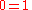
which is always false.
Therefore, there is no way for this to work, and x3 − 1 is not a linear combination of p1, p2, and p3.
The linear span
Main article: linear spanLinear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
Take an arbitrary field K, an arbitrary vector space V, and let v1,...,vn be vectors (in V).
It’s interesting to consider the set of all linear combinations of these vectors.
This set is called the linear span
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
(or just span) of the vectors, say S ={v1,...,vn}. We write the span of S as span(S) or sp(S):

Linear independence
For some sets of vectors v1,...,vn,a single vector can be written in two different ways as a linear combination of them:

Equivalently, by subtracting these (
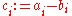 ) a non-trivial combination is zero:
) a non-trivial combination is zero:
If that is possible, then v1,...,vn are called linearly dependent; otherwise, they are linearly independent.
Similarly, we can speak of linear dependence or independence of an arbitrary set S of vectors.
If S is linearly independent and the span of S equals V, then S is a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for V.
Affine, conical, and convex combinations
By restricting the coefficients used in linear combinations, one can define the related concepts of affine combination, conical combinationConical combination
Given a finite number of vectors x_1, x_2, \dots, x_n\, in a real vector space, a conical combination or a conical sum of these vectors is a vector of the formwhere the real numbers \alpha_i\, satisfy \alpha_i\ge 0...
, and convex combination
Convex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
, and the associated notions of sets closed under these operations.
| Type of combination | Restrictions on coefficients | Name of set | Model space |
|---|---|---|---|
| Linear combination | no restrictions | Vector subspace |  |
| Affine combination | 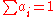 |
Affine subspace | Affine hyperplane Hyperplane A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1... |
| Conical combination Conical combination Given a finite number of vectors x_1, x_2, \dots, x_n\, in a real vector space, a conical combination or a conical sum of these vectors is a vector of the formwhere the real numbers \alpha_i\, satisfy \alpha_i\ge 0... |
 |
Convex cone Convex cone In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:... |
Quadrant Quadrant Quadrant may refer to:* A sector equal to one quarter of a circle, or half a semicircle, see Circular sector* The sectors of a two-dimensional cartesian coordinate system, see Cartesian coordinate system#Quadrants and octants... /Octant Octant An octant is one of eight divisions.-Octant in the plane :Traditionally wind direction is given as one of the 8 octants because that is more accurate than merely giving one of the 4 quadrants, and the wind vane typically does not have enough accuracy to bother with more precise indication.-Octant... |
| Convex combination Convex combination In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1.... |
 and and 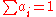 |
Convex set Convex set In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object... |
Simplex Simplex In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,... |
Because these are more restricted operations, more subsets will be closed under them, so affine subsets, convex cones, and convex sets are generalizations of vector subspaces: a vector subspace is also an affine subspace, a convex cone, and a convex set, but a convex set need not be a vector subspace, affine, or a convex cone.
These concepts often arise when one can take certain linear combinations of objects, but not any: for example, probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s are closed under convex combination (they form a convex set), but not conical or affine combinations (or linear), and positive measures are closed under conical combination but not affine or linear – hence one defines signed measure
Signed measure
In mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
s as the linear closure.
Linear and affine combinations can be defined over any field (or ring), but conical and convex combination require a notion of "positive", and hence can only be defined over an ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
(or ordered ring
Ordered ring
In abstract algebra, an ordered ring is a commutative ring R with a total order ≤ such that for all a, b, and c in R:* if a ≤ b then a + c ≤ b + c.* if 0 ≤ a and 0 ≤ b then 0 ≤ ab....
), generally the real numbers.
If one allows only scalar multiplication, not addition, one obtains a (not necessarily convex) cone
Cone (linear algebra)
In linear algebra, a cone is a subset of a vector space that is closed under multiplication by positive scalars. In other words, a subset C of a real vector space V is a cone if and only if λx belongs to C for any x in C and any positive scalar λ of V .A cone is said...
; one often restricts the definition to only allowing multiplication by positive scalars.
All of these concepts are usually defined as subsets of an ambient vector space (except for affine spaces, which are also considered as "vector spaces forgetting the origin"), rather than being axiomatized independently.
Operad theory
More abstractly, in the language of operad theoryOperad theory
Operad theory is a field of abstract algebra concerned with prototypical algebras that model properties such as commutativity or anticommutativity as well as various amounts of associativity. Operads generalize the various associativity properties already observed in algebras and coalgebras such as...
, one can consider vector spaces to be algebras
Algebra (ring theory)
In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
over the operad
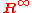 (the infinite direct sum
(the infinite direct sumDirect sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
, so only finitely many terms are non-zero; this corresponds to only taking finite sums), which parametrizes linear combinations: the vector
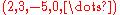 for instance corresponds to the linear combination
for instance corresponds to the linear combination 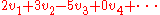 . Similarly, one can consider affine combinations, conical combinations, and convex combinations to correspond to the sub-operads where the terms sum to 1, the terms are all non-negative, or both, respectively. Graphically, these are the infinite affine hyperplane, the infinite hyper-octant, and the infinite simplex. This formalizes what is meant by
. Similarly, one can consider affine combinations, conical combinations, and convex combinations to correspond to the sub-operads where the terms sum to 1, the terms are all non-negative, or both, respectively. Graphically, these are the infinite affine hyperplane, the infinite hyper-octant, and the infinite simplex. This formalizes what is meant by  being or the standard simplex being model spaces, and such observations as that every bounded convex polytope
being or the standard simplex being model spaces, and such observations as that every bounded convex polytopeConvex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
is the image of a simplex. Here suboperads correspond to more restricted operations and thus more general theories.
From this point of view, we can think of linear combinations as the most general sort of operation on a vector space – saying that a vector space is an algebra over the operad of linear combinations is precisely the statement that all possible algebraic operations in a vector space are linear combinations.
The basic operations of addition and scalar multiplication, together with the existence of an additive identity and additive inverses, cannot be combined in any more complicated way than the generic linear combination: the basic operations are a generating set
Generating set
In mathematics, the expressions generator, generate, generated by and generating set can have several closely related technical meanings:...
for the operad of all linear combinations.
Ultimately, this fact lies at the heart of the usefulness of linear combinations in the study of vector spaces.
Generalizations
If V is a topological vector spaceTopological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
, then there may be a way to make sense of certain infinite linear combinations, using the topology of V.
For example, we might be able to speak of a1v1 + a2v2 + a3v3 + ..., going on forever.
Such infinite linear combinations do not always make sense; we call them convergent when they do.
Allowing more linear combinations in this case can also lead to a different concept of span, linear independence, and basis.
The articles on the various flavours of topological vector spaces go into more detail about these.
If K is a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
instead of a field, then everything that has been said above about linear combinations generalizes to this case without change.
The only difference is that we call spaces like V modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
instead of vector spaces.
If K is a noncommutative ring, then the concept still generalizes, with one caveat:
Since modules over noncommutative rings come in left and right versions, our linear combinations may also come in either of these versions, whatever is appropriate for the given module.
This is simply a matter of doing scalar multiplication on the correct side.
A more complicated twist comes when V is a bimodule
Bimodule
In abstract algebra a bimodule is an abelian group that is both a left and a right module, such that the left and right multiplications are compatible...
over two rings, KL and KR.
In that case, the most general linear combination looks like

where a1,...,an belong to KL, b1,...,bn belong to KR, and v1,...,vn belong to V.