Functional (mathematics)
Encyclopedia
In mathematics
, and particularly in functional analysis
, a functional is a map
from a vector space
into its underlying scalar field
. In other words, it is a function that takes a vector as its input argument, and returns a scalar. Commonly the vector space is a space of functions, thus the functional takes a function for its input-argument, then it is sometimes considered a function of a function. Its use originates in the calculus of variations
where one searches for a function that minimizes a certain functional. A particularly important application in physics
is searching for a state of a system that minimizes the energy functional
.
Transformations of functions is a rather more general concept, see Operator (mathematics).
is a function, here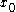
is an argument of a function 
.
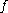At the same time, the mapping of a function to the value of the function at a point
is a functional, here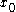
is a parameter.
Provided that f is a linear function from a linear vector space to the underlying scalar field, the above linear maps are dual
to each other, and in functional analysis both are called linear functional
s.
s such as
form a special class of functionals. They map a function f into a real number, provided that H is real-valued. Examples include
in a vector space 
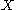, the scalar product with another vector 
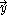, denoted 
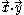or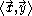 
, is a scalar. The set of vectors such that this product is zero is a vector subspace of 
, called the null space or kernel of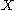 
.
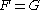between functionals can be read as an 'equation to solve', with solutions being themselves functions. In such equations there may be several sets of variable unknowns, like when it is said that an additive function 
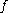is one satisfying the functional equation
.
s are used in Lagrangian mechanics
. They are derivatives of functionals: i.e. they carry information on how a functional changes, when the function changes by a small amount. See also calculus of variations
.
Richard Feynman
used functional integrals
as the central idea in his sum over the histories
formulation of quantum mechanics
. This usage implies an integral taken over some function space
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and particularly in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, a functional is a map
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
from a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
into its underlying scalar field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. In other words, it is a function that takes a vector as its input argument, and returns a scalar. Commonly the vector space is a space of functions, thus the functional takes a function for its input-argument, then it is sometimes considered a function of a function. Its use originates in the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
where one searches for a function that minimizes a certain functional. A particularly important application in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
is searching for a state of a system that minimizes the energy functional
Energy functional
Energy functional is total energy of a certain system, as a function of the system's state.In the energy methods of simulating the dynamics of complex structures, a state of the system is often described as an element of an appropriate function space. To be in this state, the system pays a certain...
.
Transformations of functions is a rather more general concept, see Operator (mathematics).
Duality
Observe that the mappingis a function, here
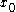is an argument of a function 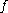.At the same time, the mapping of a function to the value of the function at a point
is a functional, here
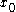is a parameter.Provided that f is a linear function from a linear vector space to the underlying scalar field, the above linear maps are dual
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
to each other, and in functional analysis both are called linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
s.
Integral
IntegralIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s such as
form a special class of functionals. They map a function f into a real number, provided that H is real-valued. Examples include
- the area underneath the graph of a positive function f
-
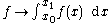
- Lp norm of functions
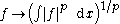
- the arclength of a curve in 2-dimensional Euclidean space
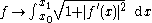
Vector scalar product
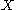Given any vector in a vector space , the scalar product with another vector 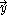, denoted 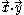or 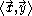, is a scalar. The set of vectors such that this product is zero is a vector subspace of , called the null space or kernel of 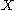.Functional equation
The traditional usage also applies when one talks about a functional equation, meaning an equation between functionals: an equation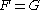 between functionals can be read as an 'equation to solve', with solutions being themselves functions. In such equations there may be several sets of variable unknowns, like when it is said that an additive function 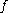is one satisfying the functional equation.Functional derivative and functional integration
Functional derivativeFunctional derivative
In mathematics and theoretical physics, the functional derivative is a generalization of the gradient. While the latter differentiates with respect to a vector with discrete components, the former differentiates with respect to a continuous function. Both of these can be viewed as extensions of...
s are used in Lagrangian mechanics
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
. They are derivatives of functionals: i.e. they carry information on how a functional changes, when the function changes by a small amount. See also calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
.
Richard Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
used functional integrals
Functional integration
Functional integration is a collection of results in mathematics and physics where the domain of an integral is no longer a region of space, but a space of functions...
as the central idea in his sum over the histories
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
formulation of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. This usage implies an integral taken over some function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
.