Algebraic number theory
Encyclopedia
Algebraic number theory is a major branch of number theory
which studies algebraic structure
s related to algebraic integer
s. This is generally accomplished by considering a ring
of algebraic integers O in an algebraic number field
K/Q, and studying their algebraic properties such as factorization
, the behaviour of ideals
, and field
extensions. In this setting, the familiar features of the integer
s—such as unique factorization—need not hold. The virtue of the primary machinery employed—Galois theory
, group cohomology
, group representation
s, and L-functions
—is that it allows one to deal with new phenomena and yet partially recover the behaviour of the usual integers.
O of an algebraic number field K is that of the unique factorization of integers into prime number
s. The prime numbers in Z are generalized to irreducible element
s in O, and though the unique factorization of elements of O into irreducible elements may hold in some cases (such as for the Gaussian integers Z[i]), it may also fail, as in the case of Z[√] where
The ideal class group
of O is a measure of how much unique factorization of elements fails; in particular, the ideal class group is trivial
if, and only if, O is a unique factorization domain
.
s (i.e. it is a Dedekind domain
). This makes the study of the prime ideals in O particularly important. This is another area where things change from Z to O: the prime numbers, which generate
prime ideals of Z (in fact, every single prime ideal of Z is of the form (p):=pZ for some prime number p,) may no longer generate prime ideals in O. For example, in the ring of Gaussian integers, the ideal 2Z[i] is no longer a prime ideal; in fact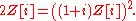
On the other hand, the ideal 3Z[i] is a prime ideal. The complete answer for the Gaussian integers is obtained by using a theorem of Fermat's, with the result being that for an odd prime number p
Generalizing this simple result to more general rings of integers is a basic problem in algebraic number theory. Class field theory
accomplishes this goal when K is an abelian extension
of Q (i.e. a Galois extension
with abelian
Galois group
).
function |·| : Q → R, there are absolute value
functions |·|p : Q → R defined for each prime number p in Z, called p-adic absolute values. Ostrowski's theorem
states that these are all possible absolute value functions on Q (up to equivalence). This suggests that the usual absolute value could be considered as another prime. More generally, a prime of an algebraic number field K (also called a place) is an equivalence class of absolute values on K. The primes in K are of two sorts:
-adic absolute values like |·|p, one for each prime ideal 
of O, and absolute values like |·| obtained by considering K as a subset of the complex number
s in various possible ways and using the absolute value |·| : C → R. A prime of the first kind is called a finite prime (or finite place) and one of the second kind is called an infinite prime (or infinite place). Thus, the set of primes of Q is generally denoted { 2, 3, 5, 7, ..., ∞ }, and the usual absolute value on Q is often denoted |·|∞ in this context.
The set of infinite primes of K can be described explicitly in terms of the embeddings K → C (i.e. the non-zero ring homomorphism
s from K to C). Specifically, the set of embeddings can be split up into two disjoint subsets, those whose image
is contained in R, and the rest. To each embedding σ : K → R, there corresponds a unique prime of K coming from the absolute value obtained by composing σ with the usual absolute value on R; a prime arising in this fashion is called a real prime (or real place). To an embedding τ : K → C whose image is not contained in R, one can construct a distinct embedding , called the conjugate embedding, by composing τ with the complex conjugation map C → C. Given such a pair of embeddings τ and , there corresponds a unique prime of K again obtained by composing τ with the usual absolute value (composing instead gives the same absolute value function since |z| = || for any complex number z, where denotes the complex conjugate of z). Such a prime is called a complex prime (or complex place). The description of the set of infinite primes is then as follows: each infinite prime corresponds either to a unique embedding σ : K → R, or a pair of conjugate embeddings τ, : K → C. The number of real (respectively, complex) primes is often denoted r1 (respectively, r2). Then, the total number of embeddings K → C is r1+2r2 (which, in fact, equals the degree of the extension K/Q).
describes the multiplicative structure of Z. It states that every non-zero integer can be written (essentially) uniquely as a product of prime power
s and ±1. The unique factorization of ideals in the ring O recovers part of this description, but fails to address the factor ±1. The integers 1 and -1 are the invertible elements (i.e. units
) of Z. More generally, the invertible elements in O form a group under multiplication called the unit group of O, denoted O×. This group can be much larger than the cyclic group
of order 2 formed by the units of Z. Dirichlet's unit theorem
describes the abstract structure of the unit group as an abelian group. A more precise statement giving the structure of O× ⊗Z Q as a Galois module
for the Galois group of K/Q is also possible. The size of the unit group, and its lattice structure give important numerical information about O, as can be seen in the class number formula
.
. If the valuation is archimedean, one gets R or C, if it is non-archimedean and lies over a prime p of the rationals, one gets a finite extension Kw / Qp: a complete, discrete valued field with finite residue field. This process simplifies the arithmetic of the field and allows the local study of problems. For example the Kronecker–Weber theorem
can be deduced easily from the analogous local statement. The philosophy behind the study of local fields is largely motivated by geometric methods. In algebraic geometry, it is common to study varieties locally at a point by localizing to a maximal ideal. Global information can then be recovered by gluing together local data. This spirit is adopted in algebraic number theory. Given a prime in the ring of algebraic integers in a number field, it is desirable to study the field locally at that prime. Therefore one localizes the ring of algebraic integers to that prime and then completes the fraction field much in the spirit of geometry.
of rank
r1 + r2 − 1 whose torsion consists of the roots of unity in O.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
which studies algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s related to algebraic integer
Algebraic integer
In number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...
s. This is generally accomplished by considering a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of algebraic integers O in an algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
K/Q, and studying their algebraic properties such as factorization
Factorization
In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...
, the behaviour of ideals
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
, and field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
extensions. In this setting, the familiar features of the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s—such as unique factorization—need not hold. The virtue of the primary machinery employed—Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
, group cohomology
Group cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
, group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
s, and L-functions
L-function
The theory of L-functions has become a very substantial, and still largely conjectural, part of contemporary analytic number theory. In it, broad generalisations of the Riemann zeta function and the L-series for a Dirichlet character are constructed, and their general properties, in most cases...
—is that it allows one to deal with new phenomena and yet partially recover the behaviour of the usual integers.
Unique factorization and the ideal class group
One of the first properties of Z that can fail in the ring of integersRing of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
O of an algebraic number field K is that of the unique factorization of integers into prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s. The prime numbers in Z are generalized to irreducible element
Irreducible element
In abstract algebra, a non-zero non-unit element in an integral domain is said to be irreducible if it is not a product of two non-units.Irreducible elements should not be confused with prime elements...
s in O, and though the unique factorization of elements of O into irreducible elements may hold in some cases (such as for the Gaussian integers Z[i]), it may also fail, as in the case of Z[√] where
The ideal class group
Ideal class group
In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
of O is a measure of how much unique factorization of elements fails; in particular, the ideal class group is trivial
Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
if, and only if, O is a unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
.
Factoring prime ideals in extensions
Unique factorization can be partially recovered for O in that it has the property of unique factorization of ideals into prime idealPrime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s (i.e. it is a Dedekind domain
Dedekind domain
In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
). This makes the study of the prime ideals in O particularly important. This is another area where things change from Z to O: the prime numbers, which generate
Principal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
prime ideals of Z (in fact, every single prime ideal of Z is of the form (p):=pZ for some prime number p,) may no longer generate prime ideals in O. For example, in the ring of Gaussian integers, the ideal 2Z[i] is no longer a prime ideal; in fact
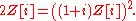
On the other hand, the ideal 3Z[i] is a prime ideal. The complete answer for the Gaussian integers is obtained by using a theorem of Fermat's, with the result being that for an odd prime number p
Generalizing this simple result to more general rings of integers is a basic problem in algebraic number theory. Class field theory
Class field theory
In mathematics, class field theory is a major branch of algebraic number theory that studies abelian extensions of number fields.Most of the central results in this area were proved in the period between 1900 and 1950...
accomplishes this goal when K is an abelian extension
Abelian extension
In abstract algebra, an abelian extension is a Galois extension whose Galois group is abelian. When the Galois group is a cyclic group, we have a cyclic extension. More generally, a Galois extension is called solvable if its Galois group is solvable....
of Q (i.e. a Galois extension
Galois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
with abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
).
Primes and places
An important generalization of the notion of prime ideal in O is obtained by passing from the so-called ideal-theoretic approach to the so-called valuation-theoretic approach. The relation between the two approaches arises as follows. In addition to the usual absolute valueAbsolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
function |·| : Q → R, there are absolute value
Absolute value (algebra)
In mathematics, an absolute value is a function which measures the "size" of elements in a field or integral domain. More precisely, if D is an integral domain, then an absolute value is any mapping | x | from D to the real numbers R satisfying:* | x | ≥ 0,*...
functions |·|p : Q → R defined for each prime number p in Z, called p-adic absolute values. Ostrowski's theorem
Ostrowski's theorem
Ostrowski's theorem, due to Alexander Ostrowski , states that any non-trivial absolute value on the rational numbers Q is equivalent to either the usual real absolute value or a p-adic absolute value.- Definitions :...
states that these are all possible absolute value functions on Q (up to equivalence). This suggests that the usual absolute value could be considered as another prime. More generally, a prime of an algebraic number field K (also called a place) is an equivalence class of absolute values on K. The primes in K are of two sorts:
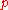-adic absolute values like |·|p, one for each prime ideal 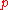of O, and absolute values like |·| obtained by considering K as a subset of the complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s in various possible ways and using the absolute value |·| : C → R. A prime of the first kind is called a finite prime (or finite place) and one of the second kind is called an infinite prime (or infinite place). Thus, the set of primes of Q is generally denoted { 2, 3, 5, 7, ..., ∞ }, and the usual absolute value on Q is often denoted |·|∞ in this context.
The set of infinite primes of K can be described explicitly in terms of the embeddings K → C (i.e. the non-zero ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
s from K to C). Specifically, the set of embeddings can be split up into two disjoint subsets, those whose image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
is contained in R, and the rest. To each embedding σ : K → R, there corresponds a unique prime of K coming from the absolute value obtained by composing σ with the usual absolute value on R; a prime arising in this fashion is called a real prime (or real place). To an embedding τ : K → C whose image is not contained in R, one can construct a distinct embedding , called the conjugate embedding, by composing τ with the complex conjugation map C → C. Given such a pair of embeddings τ and , there corresponds a unique prime of K again obtained by composing τ with the usual absolute value (composing instead gives the same absolute value function since |z| = || for any complex number z, where denotes the complex conjugate of z). Such a prime is called a complex prime (or complex place). The description of the set of infinite primes is then as follows: each infinite prime corresponds either to a unique embedding σ : K → R, or a pair of conjugate embeddings τ, : K → C. The number of real (respectively, complex) primes is often denoted r1 (respectively, r2). Then, the total number of embeddings K → C is r1+2r2 (which, in fact, equals the degree of the extension K/Q).
Units
The fundamental theorem of arithmeticFundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
describes the multiplicative structure of Z. It states that every non-zero integer can be written (essentially) uniquely as a product of prime power
Prime power
In mathematics, a prime power is a positive integer power of a prime number.For example: 5=51, 9=32 and 16=24 are prime powers, while6=2×3, 15=3×5 and 36=62=22×32 are not...
s and ±1. The unique factorization of ideals in the ring O recovers part of this description, but fails to address the factor ±1. The integers 1 and -1 are the invertible elements (i.e. units
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
) of Z. More generally, the invertible elements in O form a group under multiplication called the unit group of O, denoted O×. This group can be much larger than the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order 2 formed by the units of Z. Dirichlet's unit theorem
Dirichlet's unit theorem
In mathematics, Dirichlet's unit theorem is a basic result in algebraic number theory due to Gustav Lejeune Dirichlet. It determines the rank of the group of units in the ring OK of algebraic integers of a number field K...
describes the abstract structure of the unit group as an abelian group. A more precise statement giving the structure of O× ⊗Z Q as a Galois module
Galois module
In mathematics, a Galois module is a G-module where G is the Galois group of some extension of fields. The term Galois representation is frequently used when the G-module is a vector space over a field or a free module over a ring, but can also be used as a synonym for G-module...
for the Galois group of K/Q is also possible. The size of the unit group, and its lattice structure give important numerical information about O, as can be seen in the class number formula
Class number formula
In number theory, the class number formula relates many important invariants of a number field to a special value of its Dedekind zeta function-General statement of the class number formula:...
.
Local fields
Completing a number field K at a place w gives a complete fieldComplete field
In mathematics, a complete field is a field equipped with a metric and complete with respect to that metric. Basic examples include the real numbers, the complex numbers, and complete valued fields .- See also :...
. If the valuation is archimedean, one gets R or C, if it is non-archimedean and lies over a prime p of the rationals, one gets a finite extension Kw / Qp: a complete, discrete valued field with finite residue field. This process simplifies the arithmetic of the field and allows the local study of problems. For example the Kronecker–Weber theorem
Kronecker–Weber theorem
In algebraic number theory, the Kronecker–Weber theorem states that every finite abelian extension of the field of rational numbers Q, or in other words, every algebraic number field whose Galois group over Q is abelian, is a subfield of a cyclotomic field, i.e. a field obtained by adjoining a root...
can be deduced easily from the analogous local statement. The philosophy behind the study of local fields is largely motivated by geometric methods. In algebraic geometry, it is common to study varieties locally at a point by localizing to a maximal ideal. Global information can then be recovered by gluing together local data. This spirit is adopted in algebraic number theory. Given a prime in the ring of algebraic integers in a number field, it is desirable to study the field locally at that prime. Therefore one localizes the ring of algebraic integers to that prime and then completes the fraction field much in the spirit of geometry.
Finiteness of the class group
One of the classical results in algebraic number theory is that the ideal class group of an algebraic number field K is finite. The order of the class group is called the class number, and is often denoted by the letter h.Dirichlet's unit theorem
Dirichlet's unit theorem provides a description of the structure of the multiplicative group of units O× of the ring of integers O. Specifically, it states that O× is isomorphic to G × Zr, where G is the finite cyclic group consisting of all the roots of unity in O, and r = r1 + r2 − 1 (where r1 (respectively, r2) denotes the number of real embeddings (respectively, pairs of conjugate non-real embeddings) of K). In other words, O× is a finitely generated abelian groupFinitely generated abelian group
In abstract algebra, an abelian group is called finitely generated if there exist finitely many elements x1,...,xs in G such that every x in G can be written in the formwith integers n1,...,ns...
of rank
Rank of an abelian group
In mathematics, the rank, Prüfer rank, or torsion-free rank of an abelian group A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group contained in A. If A is torsion-free then it embeds into a vector space over the...
r1 + r2 − 1 whose torsion consists of the roots of unity in O.
Artin reciprocity
See also- Quadratic reciprocityQuadratic reciprocityIn number theory, the law of quadratic reciprocity is a theorem about modular arithmetic which gives conditions for the solvability of quadratic equations modulo prime numbers...
- Cubic reciprocityCubic reciprocityCubic reciprocity is a collection of theorems in elementary and algebraic number theory that state conditions under which the congruence x3 ≡ p is solvable; the word "reciprocity" comes from the form of the main theorem, which states that if p and q are primary numbers in the...
- Quartic reciprocityQuartic reciprocityQuartic or biquadratic reciprocity is a collection of theorems in elementary and algebraic number theory that state conditions under which the congruence x4 ≡ p is solvable; the word "reciprocity" comes from the form of some of these theorems, in that they relate the solvability of the...
Introductory texts
- Kenneth Ireland and Michael Rosen, "A Classical Introduction to Modern Number Theory, Second Edition", Springer-Verlag, 1990
- Ian StewartIan Stewart (mathematician)Ian Nicholas Stewart FRS is a professor of mathematics at the University of Warwick, England, and a widely known popular-science and science-fiction writer. He is the first recipient of the , awarded jointly by the LMS and the IMA for his work on promoting mathematics.-Biography:Stewart was born...
and David O. TallDavid O. TallDavid Orme Tall is a mathematics education theorist at the University of Warwick. One of his most influential works is the joint paper with Vinner Concept image and concept definition.... The "concept image" is a notion in cognitive theory. It consists of all the cognitive structure in the...
, "Algebraic Number Theory and Fermat's Last Theorem," A. K. Peters, 2002
See also
- Arithmétique modulaire A survey of number theory, with applications (in French Wikipedia)
- Langlands programLanglands programThe Langlands program is a web of far-reaching and influential conjectures that relate Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups over local fields and adeles. It was proposed by ....
- Adele ringAdele ringIn algebraic number theory and topological algebra, the adele ring is a topological ring which is built on the field of rational numbers . It involves all the completions of the field....
- Tamagawa number
- Iwasawa theoryIwasawa theoryIn number theory, Iwasawa theory is the study of objects of arithmetic interest over infinite towers of number fields. It began as a Galois module theory of ideal class groups, initiated by Kenkichi Iwasawa, in the 1950s, as part of the theory of cyclotomic fields. In the early 1970s, Barry Mazur...
- Arithmetic algebraic geometry