
Inverse element
Encyclopedia
In abstract algebra
, the idea of an inverse element generalises the concept of a negation
, in relation to addition
, and a reciprocal
, in relation to multiplication
. The intuition is of an element that can 'undo' the effect of combination with another given element. While the precise definition of an inverse element varies depending on the algebraic structure involved, these definitions coincide in a group
.
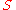 be a set with a binary operation
be a set with a binary operation
 (i.e., a magma
(i.e., a magma
). If is an identity element
is an identity element
of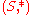 (i.e., S is an unital magma) and
(i.e., S is an unital magma) and  , then
, then  is called a left inverse of
is called a left inverse of  and
and  is called a right inverse of
is called a right inverse of  . If an element
. If an element  is both a left inverse and a right inverse of
is both a left inverse and a right inverse of 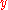 , then
, then  is called a two-sided inverse, or simply an inverse, of
is called a two-sided inverse, or simply an inverse, of 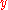 . An element with a two-sided inverse in
. An element with a two-sided inverse in 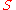 is called invertible in
is called invertible in 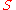 . An element with an inverse element only on one side is left invertible, resp. right invertible. If all elements in S are invertible, S is called a loop
. An element with an inverse element only on one side is left invertible, resp. right invertible. If all elements in S are invertible, S is called a loop
.
Just like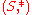 can have several left identities or several right identities, it is possible for an element to have several left inverses or several right inverses (but note that their definition above uses a two-sided identity
can have several left identities or several right identities, it is possible for an element to have several left inverses or several right inverses (but note that their definition above uses a two-sided identity  ). It can even have several left inverses and several right inverses.
). It can even have several left inverses and several right inverses.
If the operation is associative then if an element has both a left inverse and a right inverse, they are equal. In other words, in a monoid
is associative then if an element has both a left inverse and a right inverse, they are equal. In other words, in a monoid
every element has at most one inverse (as defined in this section). In a monoid, the set of (left and right) invertible elements is a group
, called the group of units of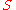 , and denoted by
, and denoted by 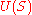 or H1.
or H1.
A left-invertible element is left-cancellative
, and analogously for right and two-sided.
.
In a semigroup an element x is called (von Neumann) regular if there exists some element z in S such that xzx = x; z is sometimes called a pseudoinverse. An element y is called (simply) an inverse of x if xyx = x and y = yxy. Every regular element has at least one inverse: if x = xzx then it is easy to verify that y = zxz is an inverse of x as defined in this section. Another easy to prove fact: if y is an inverse of x then e = xy and f = yx are idempotents, that is ee = e and ff = f. Thus, every pair of (mutually) inverse elements gives rise to two idempotents, and ex = xf = x, ye = fy = y, and e acts as a left identity on x, while f acts a right identity, and the left/right roles are reversed for y. This simple observation can be generalized using Green's relations
an element x is called (von Neumann) regular if there exists some element z in S such that xzx = x; z is sometimes called a pseudoinverse. An element y is called (simply) an inverse of x if xyx = x and y = yxy. Every regular element has at least one inverse: if x = xzx then it is easy to verify that y = zxz is an inverse of x as defined in this section. Another easy to prove fact: if y is an inverse of x then e = xy and f = yx are idempotents, that is ee = e and ff = f. Thus, every pair of (mutually) inverse elements gives rise to two idempotents, and ex = xf = x, ye = fy = y, and e acts as a left identity on x, while f acts a right identity, and the left/right roles are reversed for y. This simple observation can be generalized using Green's relations
: every idempotent e in an arbitrary semigroup is a left identity for Re and right identity for Le. An intuitive description of this is fact is that every pair of mutually inverse elements produces a local left identity, and respectively, a local right identity.
In a monoid, the notion of inverse as defined in the previous section is strictly narrower than the definition given in this section. Only elements in H1 have an inverse from the unital magma perspective, whereas for any idempotent e, the elements of He have an inverse as defined in this section. Under this more general definition, inverses need not be unique (or exist) in an arbitrary semigroup or monoid. If all elements are regular, then the semigroup (or monoid) is called regular, and every element has at least one inverse. If every element has exactly one inverse as defined in this section, then the semigroup is called an inverse semigroup
. Finally, an inverse semigroup with only one idempotent is a group. An inverse semigroup may have an absorbing element
0 because 000=0, whereas a group may not.
Outside semigroup theory, a unique inverse as defined in this section is sometimes called a quasi-inverse. This is generally justified because in most applications (e.g. all examples in this article) associativity holds, which makes this notion a generalization of the left/right inverse relative to an identity.
*-semigroups
, in which the interaction axiom is (ab)° = b°a°. Such an operation is called an involution, and typically denoted by a *.
Clearly a group is both an I-semigroup and a *-semigroup. Inverse semigroups are exactly those semigroups that are both I-semigroups and *-semigroups. A class of semigroups important in semigroup theory are completely regular semigroup
s; these are I-semigroups in which one additionally has aa° = a°a; in other words every element has commuting pseudoinverse a°. There are few concrete examples of such semigroups however; most are completely simple semigroups. In contrast, a class of *-semigroups, the *-regular semigroups, yield one of best known examples of a (unique) pseudoinverse, the Moore–Penrose inverse. In this case however the involution a* is not the pseudoinverse. Rather, the pseudoinverse of x is the unique element y such that xyx = x, yxy = y, (xy)* = xy, (yx)* = yx. Since *-regular semigroups generalize inverse semigroups, the unique element defined this way in a *-regular semigroup is called the generalized inverse or Penrose-Moore inverse. In a *-regular semigroup S one can identify a special subset of idempotents F(S) called a P-system; every element a of the semigroup has exactly one inverse a* such that aa* and a*a are in F(S). The P-systems of Yamada are based upon the notion of regular *-semigroup as defined by Nordahl and Scheiblich.
 has an additive inverse
has an additive inverse
(i.e. an inverse with respect to addition
) given by . Every nonzero real number
. Every nonzero real number  has a multiplicative inverse
has a multiplicative inverse
(i.e. an inverse with respect to multiplication
) given by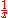 (or
(or 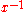 ). By contrast, zero
). By contrast, zero
has no multiplicative inverse, but it has a unique quasi-inverse, 0 itself.
 is the left (resp. right) inverse of a function
is the left (resp. right) inverse of a function
 (for function composition
(for function composition
), if and only if (resp.
(resp.  ) is the identity function
) is the identity function
on the domain
(resp. codomain
) of . The inverse of a function
. The inverse of a function  is often written
is often written 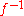 , but this notation is sometimes ambiguous. Only bijection
, but this notation is sometimes ambiguous. Only bijection
s have two-sided inverses, but any function has a quasi-inverse, i.e. the full transformation monoid is regular. The monoid of partial functions is also regular, whereas the monoid of injective partial transformations is the prototypical inverse semigroup.
, L and G are quasi-inverses of each other, i.e. LGL = L and GLG = G and one uniquely determines the other. They are not left or right inverses of each other however.
 with entries in a field
with entries in a field
 is invertible (in the set of all square matrices of the same size, under matrix multiplication
is invertible (in the set of all square matrices of the same size, under matrix multiplication
) if and only if its determinant
is different from zero. If the determinant of is zero, it is impossible for it to have a one-sided inverse; therefore a left inverse or right inverse implies the existence of the other one. See invertible matrix for more.
is zero, it is impossible for it to have a one-sided inverse; therefore a left inverse or right inverse implies the existence of the other one. See invertible matrix for more.
More generally, a square matrix over a commutative ring
 is invertible if and only if
is invertible if and only if
its determinant is invertible in .
.
Non-square matrices of full rank have one-sided inverses:
The right inverse can be used to determine the least norm solution of Ax = b.
No rank-deficient matrix has any (even one-sided) inverse. However, the Moore–Penrose pseudoinverse exists for all matrices, and coincides with the left or right (or true) inverse when it exists.
As an example of matrix inverses, consider:
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the idea of an inverse element generalises the concept of a negation
Additive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
, in relation to addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, and a reciprocal
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
, in relation to multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
. The intuition is of an element that can 'undo' the effect of combination with another given element. While the precise definition of an inverse element varies depending on the algebraic structure involved, these definitions coincide in a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
.
In an unital magma
Let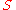 be a set with a binary operation
be a set with a binary operationBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
 (i.e., a magma
(i.e., a magmaMagma (algebra)
In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
). If
 is an identity element
is an identity elementIdentity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
of
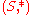 (i.e., S is an unital magma) and
(i.e., S is an unital magma) and  , then
, then  is called a left inverse of
is called a left inverse of  and
and  is called a right inverse of
is called a right inverse of  . If an element
. If an element  is both a left inverse and a right inverse of
is both a left inverse and a right inverse of 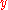 , then
, then  is called a two-sided inverse, or simply an inverse, of
is called a two-sided inverse, or simply an inverse, of 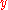 . An element with a two-sided inverse in
. An element with a two-sided inverse in 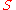 is called invertible in
is called invertible in 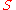 . An element with an inverse element only on one side is left invertible, resp. right invertible. If all elements in S are invertible, S is called a loop
. An element with an inverse element only on one side is left invertible, resp. right invertible. If all elements in S are invertible, S is called a loopQuasigroup
In mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...
.
Just like
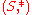 can have several left identities or several right identities, it is possible for an element to have several left inverses or several right inverses (but note that their definition above uses a two-sided identity
can have several left identities or several right identities, it is possible for an element to have several left inverses or several right inverses (but note that their definition above uses a two-sided identity  ). It can even have several left inverses and several right inverses.
). It can even have several left inverses and several right inverses.If the operation
 is associative then if an element has both a left inverse and a right inverse, they are equal. In other words, in a monoid
is associative then if an element has both a left inverse and a right inverse, they are equal. In other words, in a monoidMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
every element has at most one inverse (as defined in this section). In a monoid, the set of (left and right) invertible elements is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, called the group of units of
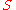 , and denoted by
, and denoted by 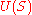 or H1.
or H1.A left-invertible element is left-cancellative
Cancellation property
In mathematics, the notion of cancellative is a generalization of the notion of invertible.An element a in a magma has the left cancellation property if for all b and c in M, a * b = a * c always implies b = c.An element a in a magma has the right cancellation...
, and analogously for right and two-sided.
In a semigroup
The definition in the previous section generalizes the notion of inverse in group relative to the notion of identity. It's also possible, albeit less obvious, to generalize the notion of an inverse by dropping the identity element but keeping associativity, i.e. in a semigroupSemigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
.
In a semigroup
 an element x is called (von Neumann) regular if there exists some element z in S such that xzx = x; z is sometimes called a pseudoinverse. An element y is called (simply) an inverse of x if xyx = x and y = yxy. Every regular element has at least one inverse: if x = xzx then it is easy to verify that y = zxz is an inverse of x as defined in this section. Another easy to prove fact: if y is an inverse of x then e = xy and f = yx are idempotents, that is ee = e and ff = f. Thus, every pair of (mutually) inverse elements gives rise to two idempotents, and ex = xf = x, ye = fy = y, and e acts as a left identity on x, while f acts a right identity, and the left/right roles are reversed for y. This simple observation can be generalized using Green's relations
an element x is called (von Neumann) regular if there exists some element z in S such that xzx = x; z is sometimes called a pseudoinverse. An element y is called (simply) an inverse of x if xyx = x and y = yxy. Every regular element has at least one inverse: if x = xzx then it is easy to verify that y = zxz is an inverse of x as defined in this section. Another easy to prove fact: if y is an inverse of x then e = xy and f = yx are idempotents, that is ee = e and ff = f. Thus, every pair of (mutually) inverse elements gives rise to two idempotents, and ex = xf = x, ye = fy = y, and e acts as a left identity on x, while f acts a right identity, and the left/right roles are reversed for y. This simple observation can be generalized using Green's relationsGreen's relations
In mathematics, Green's relations are five equivalence relations that characterise the elements of a semigroup in terms of the principal ideals they generate. The relations are named for James Alexander Green, who introduced them in a paper of 1951...
: every idempotent e in an arbitrary semigroup is a left identity for Re and right identity for Le. An intuitive description of this is fact is that every pair of mutually inverse elements produces a local left identity, and respectively, a local right identity.
In a monoid, the notion of inverse as defined in the previous section is strictly narrower than the definition given in this section. Only elements in H1 have an inverse from the unital magma perspective, whereas for any idempotent e, the elements of He have an inverse as defined in this section. Under this more general definition, inverses need not be unique (or exist) in an arbitrary semigroup or monoid. If all elements are regular, then the semigroup (or monoid) is called regular, and every element has at least one inverse. If every element has exactly one inverse as defined in this section, then the semigroup is called an inverse semigroup
Inverse semigroup
In mathematics, an inverse semigroup S is a semigroup in which every element x in S has a unique inversey in S in the sense that x = xyx and y = yxy...
. Finally, an inverse semigroup with only one idempotent is a group. An inverse semigroup may have an absorbing element
Absorbing element
In mathematics, an absorbing element is a special type of element of a set with respect to a binary operation on that set. The result of combining an absorbing element with any element of the set is the absorbing element itself. In semigroup theory, the absorbing element is called a zero element...
0 because 000=0, whereas a group may not.
Outside semigroup theory, a unique inverse as defined in this section is sometimes called a quasi-inverse. This is generally justified because in most applications (e.g. all examples in this article) associativity holds, which makes this notion a generalization of the left/right inverse relative to an identity.
U-semigroups
A natural generalization of the inverse semigroup is to define an (arbitrary) unary operation ° such that (a°)°=a for all a in S; this endows S with a type <2,1> algebra. A semigroup endowed with such an operation is called a U-semigroup. Although it may seem that a° will be the inverse of a, this is not necessarily the case. In order to obtain interesting notion(s), the unary operation must somehow interact with the semigroup operation. Two classes of U-semigroups have been studied:Semigroup with involution
In mathematics, in semigroup theory, an involution in a semigroup is a transformation of the semigroup which is its own inverse and which is an anti-automorphism of the semigroup. A semigroup in which an involution is defined is called a semigroup with involution...
, in which the interaction axiom is (ab)° = b°a°. Such an operation is called an involution, and typically denoted by a *.
Clearly a group is both an I-semigroup and a *-semigroup. Inverse semigroups are exactly those semigroups that are both I-semigroups and *-semigroups. A class of semigroups important in semigroup theory are completely regular semigroup
Completely regular semigroup
In mathematics, a completely regular semigroup is a semigroup in which every element is in some subgroup of the semigroup. The class of completely regular semigroups forms an important subclass of the class of regular semigroups, the class of inverse semigroups being another such subclass...
s; these are I-semigroups in which one additionally has aa° = a°a; in other words every element has commuting pseudoinverse a°. There are few concrete examples of such semigroups however; most are completely simple semigroups. In contrast, a class of *-semigroups, the *-regular semigroups, yield one of best known examples of a (unique) pseudoinverse, the Moore–Penrose inverse. In this case however the involution a* is not the pseudoinverse. Rather, the pseudoinverse of x is the unique element y such that xyx = x, yxy = y, (xy)* = xy, (yx)* = yx. Since *-regular semigroups generalize inverse semigroups, the unique element defined this way in a *-regular semigroup is called the generalized inverse or Penrose-Moore inverse. In a *-regular semigroup S one can identify a special subset of idempotents F(S) called a P-system; every element a of the semigroup has exactly one inverse a* such that aa* and a*a are in F(S). The P-systems of Yamada are based upon the notion of regular *-semigroup as defined by Nordahl and Scheiblich.
Examples
All examples in this section involve associative operators, thus we shall use the terms left/right inverse for the unital magma-based definition, and quasi-inverse for its more general version.Real numbers
Every real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
 has an additive inverse
has an additive inverseAdditive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
(i.e. an inverse with respect to addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
) given by
 . Every nonzero real number
. Every nonzero real number  has a multiplicative inverse
has a multiplicative inverseMultiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
(i.e. an inverse with respect to multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
) given by
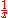 (or
(or 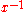 ). By contrast, zero
). By contrast, zero0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
has no multiplicative inverse, but it has a unique quasi-inverse, 0 itself.
Functions and partial functions
A function is the left (resp. right) inverse of a function
is the left (resp. right) inverse of a functionInverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
 (for function composition
(for function compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
), if and only if
 (resp.
(resp.  ) is the identity function
) is the identity functionIdentity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
(resp. codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
) of
 . The inverse of a function
. The inverse of a function  is often written
is often written 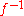 , but this notation is sometimes ambiguous. Only bijection
, but this notation is sometimes ambiguous. Only bijectionBijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
s have two-sided inverses, but any function has a quasi-inverse, i.e. the full transformation monoid is regular. The monoid of partial functions is also regular, whereas the monoid of injective partial transformations is the prototypical inverse semigroup.
Galois connections
The lower and upper adjoints in a (monotone) Galois connectionGalois connection
In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
, L and G are quasi-inverses of each other, i.e. LGL = L and GLG = G and one uniquely determines the other. They are not left or right inverses of each other however.
Matrices
A square matrix with entries in a field
with entries in a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
 is invertible (in the set of all square matrices of the same size, under matrix multiplication
is invertible (in the set of all square matrices of the same size, under matrix multiplicationMatrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
) if and only if its determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
is different from zero. If the determinant of
 is zero, it is impossible for it to have a one-sided inverse; therefore a left inverse or right inverse implies the existence of the other one. See invertible matrix for more.
is zero, it is impossible for it to have a one-sided inverse; therefore a left inverse or right inverse implies the existence of the other one. See invertible matrix for more.More generally, a square matrix over a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
 is invertible if and only if
is invertible if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
its determinant is invertible in
 .
.Non-square matrices of full rank have one-sided inverses:
- For
 we have a left inverse:
we have a left inverse: 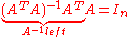
- For
 we have a right inverse:
we have a right inverse: 
The right inverse can be used to determine the least norm solution of Ax = b.
No rank-deficient matrix has any (even one-sided) inverse. However, the Moore–Penrose pseudoinverse exists for all matrices, and coincides with the left or right (or true) inverse when it exists.
As an example of matrix inverses, consider:
-
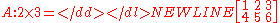
So, as m < n, we have a right inverse.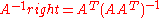
-

-

The left inverse doesn't exist, because
-

which is a singular matrix, and cannot be inverted.
-
-
-

