
Banach space
Encyclopedia
In mathematics
, Banach spaces is the name for complete normed vector space
s, one of the central objects of study in functional analysis
. A complete normed vector space is a vector space
V with a norm
||·|| such that every Cauchy sequence
(with respect to the metric
d(x, y) = ||x − y||) in V has a limit
in V (with respect to the topology
induced by that metric). As for general vector spaces, a Banach space over the real number
s is called a real Banach space, and a Banach space over the complex numbers is called a complex Banach space.
Many of the infinite-dimensional function space
s studied in analysis are Banach spaces, including spaces of continuous function
s (continuous functions on a compact Hausdorff space
), spaces of Lebesgue integrable functions known as Lp spaces
, and spaces of holomorphic function
s known as Hardy space
s. They are the most commonly used topological vector space
s, and their topology comes from a norm
.
They are named after the Polish mathematician Stefan Banach
, who introduced them in 1920–1922 along with Hans Hahn
and Eduard Helly
.
R or C.
The familiar Euclidean space
s Kn, where the Euclidean norm of x = (x1, …, xn) is given by ||x|| = (x12+…+ xn2)1/2, are Banach spaces. Hence every finite-dimensional K vector space becomes a Banach space being endowed with an arbitrary norm, since all norms are equivalent on a finite-dimensional K vector space.
Consider the space of all continuous function
s ƒ : [a, b] → K defined on a closed interval [a, b]. This space becomes a Banach space if an appropriate norm ||ƒ||, is defined in it. Such a norm may be defined as ||ƒ|| = sup { |ƒ(x)| : x ∈ [a, b] }, known as the supremum norm. This is indeed a well-defined norm, since continuous functions defined on a closed interval are bounded.
Since ƒ is a continuous function on a closed interval, then it is bounded and the supremum in the above definition is attained by the Weierstrass extreme value theorem
, so we can replace the supremum by the maximum. In this case, the norm is also called the maximum norm.
The space is complete under this norm, and the resulting Banach space is denoted by C[a, b]. This example can be generalized to the space C(X) of all continuous functions X → K, where X is a compact space
, or to the space of all bounded continuous functions X → K, where X is any topological space
, or indeed to the space B(X) of all bounded functions X → K, where X is any set. In all these examples, we can even multiply functions and stay in the same space: all these examples are in fact unital Banach algebra
s.
For any open set
Ω ⊆ C, the set A(Ω) of all bounded, analytic function
s u : Ω → C is a complex Banach space with respect to the supremum norm. The fact that uniform limits of analytic functions are analytic is an easy consequence of Morera's theorem
.
If p ≥ 0 is a real number, we can consider the space of all infinite sequence
s (x1, x2, x3, …) of elements in K such that the infinite series ∑i |xi|p is finite. The p-th root of this series' value is then defined to be the p-norm of the sequence. The space, together with this norm, is a Banach space; it is denoted by ℓ p.
The Banach space ℓ∞ consists of all bounded sequences of elements in K; the norm of such a sequence is defined to be the supremum of the absolute values of the sequence's members.
Again, if p ≥ 1 is a real number, we can consider all functions ƒ : [a, b] → K such that |ƒ|p is Lebesgue integrable
. The p-th root of this integral is then defined to be the norm of ƒ. By itself, this space is not a Banach space because there are non-zero functions whose norm is zero. We define an equivalence relation
as follows: ƒ and g are equivalent if and only if
the norm of ƒ−g is zero. The set of equivalence classes then forms a Banach space; it is denoted by Lp([a, b]). It is crucial to use the Lebesgue integral and not the Riemann integral here, because the Riemann integral would not yield a complete space. These examples can be generalized; see Lp spaces
for details.
If X and Y are two Banach spaces, then we can form their direct sum X ⊕ Y, which has a natural topological vector space structure but no canonical norm. However, it is again a Banach space for several equivalent norms, for example
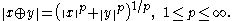
This construction can be generalized to define ℓp-direct sums of arbitrarily many Banach spaces. When there is an infinite number of non-zero summands, the space obtained in this way depends upon p.
If M is a closed linear subspace
of the Banach space X, then the quotient space
X / M is again a Banach space.
Every inner product gives rise to an associated norm. The inner product space is called a Hilbert space
if its associated norm is complete. Thus every Hilbert space is a Banach space by definition. The converse statement also holds under certain conditions; see below.
K-linear maps
A : V → W
is denoted by L(V, W). In infinite-dimensional spaces, not all linear maps are automatically continuous. In general, a linear mapping on a normed space is continuous if and only if it is bounded
on the closed unit ball. Thus the vector space L(V, W) can be given the operator norm
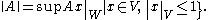
With respect to this norm, L(V,W) is a Banach space. This is also true under the less restrictive condition that V be a normed space.
When V = W, the space L(V) = L(V, V) forms a unital Banach algebra
; the multiplication operation is given by the composition of linear maps.
(either the real
or the complex
numbers), then K is itself a Banach space (using the absolute value
as norm) and we can define the dual space
V′ as V′ = L(V, K), the space of continuous linear maps into K. This is again a Banach space (with the operator norm
). It can be used to define a new topology
on V: the weak topology
.
Note that the requirement that the maps be continuous is essential; if V is infinite-dimensional, there exist linear maps which are not continuous, and therefore not bounded
, so the space V∗ of linear maps into K is not a Banach space. The space V∗ (which may be called the algebraic dual space to distinguish it from V' ) also induces a weak topology which is finer than that induced by the continuous dual since .
There is a natural map F from V to V′′ (the dual of the dual) defined by
for all x in V and ƒ in V′ . Because F(x) is a map from V′ to K, it is an element of V′′ . The map F: x → F(x) is thus a map V → V′′ . As a consequence of the Hahn–Banach theorem
, this map is injective, and isometric; if it is also surjective, then the Banach space V is called reflexive
. Reflexive spaces have many important geometric properties. A space is reflexive if and only if its dual is reflexive, which is the case if and only if its unit ball is compact
in the weak topology
.
For example, ℓp is reflexive for 1 < p < ∞ but ℓ1 and ℓ∞ are not reflexive. When p < ∞, the dual of ℓp is ℓq where p and q are related by the formula 1/p + 1/q = 1. See L p spaces
for details.
is a Banach space because, by definition, a Hilbert space is complete with respect to the norm associated with its inner product, where a norm and an inner product are said to be associated if ||v||² = (v,v) for all v.
The converse is not always true; not every Banach space is a Hilbert space. A necessary and sufficient condition for a Banach space V to be associated to an inner product (which will then necessarily make V into a Hilbert space) is the parallelogram identity:

for all u and v in V, and where ||*|| is the norm on V. So, for example, while Rn is a Banach space with respect to any norm defined on it, it is only a Hilbert space with respect to the Euclidean norm. Similarly, as an infinite-dimensional example, the Lebesgue space Lp is always a Banach space but is only a Hilbert space when p = 2.
If the norm of a Banach space satisfies this identity, the associated inner product which makes it into a Hilbert space is given by the polarization identity
. If V is a real Banach space, then the polarization identity is
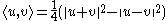
whereas if V is a complex Banach space, then the polarization identity is given by (assuming that scalar product is linear in first argument):
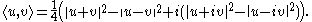
The necessity of this condition follows easily from the properties of an inner product. To see that it is sufficient—that the parallelogram law implies that the form defined by the polarization identity is indeed a complete inner product—one verifies algebraically that this form is additive, whence it follows by induction
that the form is linear over the integers and rationals. Then since every real is the limit of some Cauchy sequence of rationals, the completeness of the norm extends the linearity to the whole real line. In the complex case, one can check also that the bilinear form is linear over i in one argument, and conjugate linear in the other.
that a Hamel basis of an infinite-dimensional Banach space is uncountable.
and the Gâteaux derivative
.
on R, are complete but are not normed vector spaces and hence not Banach spaces. In Fréchet space
s one still has a complete metric
, while LF-space
s are complete uniform
vector spaces arising as limits of Fréchet spaces.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Banach spaces is the name for complete normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
s, one of the central objects of study in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
. A complete normed vector space is a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V with a norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
||·|| such that every Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
(with respect to the metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
d(x, y) = ||x − y||) in V has a limit
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
in V (with respect to the topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
induced by that metric). As for general vector spaces, a Banach space over the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s is called a real Banach space, and a Banach space over the complex numbers is called a complex Banach space.
Many of the infinite-dimensional function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
s studied in analysis are Banach spaces, including spaces of continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s (continuous functions on a compact Hausdorff space
Continuous functions on a compact Hausdorff space
In mathematical analysis, and especially functional analysis, a fundamental role is played by the space of continuous functions on a compact Hausdorff space with values in the real or complex numbers. This space, denoted by C, is a vector space with respect to the pointwise addition of functions...
), spaces of Lebesgue integrable functions known as Lp spaces
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
, and spaces of holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s known as Hardy space
Hardy space
In complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
s. They are the most commonly used topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s, and their topology comes from a norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
.
They are named after the Polish mathematician Stefan Banach
Stefan Banach
Stefan Banach was a Polish mathematician who worked in interwar Poland and in Soviet Ukraine. He is generally considered to have been one of the 20th century's most important and influential mathematicians....
, who introduced them in 1920–1922 along with Hans Hahn
Hans Hahn
Hans Hahn was an Austrian mathematician who made contributions to functional analysis, topology, set theory, the calculus of variations, real analysis, and order theory.-Biography:...
and Eduard Helly
Eduard Helly
Eduard Helly was a mathematician and the eponym of Helly's theorem, Helly families, Helly's selection theorem, Helly metric, and the Helly–Bray theorem. In 1912, Helly published a proof of Hahn–Banach theorem, 15 years before Hahn and Banach discovered it independently...
.
Examples
Throughout, let K stand for one of the fieldsField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
R or C.
The familiar Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s Kn, where the Euclidean norm of x = (x1, …, xn) is given by ||x|| = (x12+…+ xn2)1/2, are Banach spaces. Hence every finite-dimensional K vector space becomes a Banach space being endowed with an arbitrary norm, since all norms are equivalent on a finite-dimensional K vector space.
Consider the space of all continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s ƒ : [a, b] → K defined on a closed interval [a, b]. This space becomes a Banach space if an appropriate norm ||ƒ||, is defined in it. Such a norm may be defined as ||ƒ|| = sup { |ƒ(x)| : x ∈ [a, b] }, known as the supremum norm. This is indeed a well-defined norm, since continuous functions defined on a closed interval are bounded.
Since ƒ is a continuous function on a closed interval, then it is bounded and the supremum in the above definition is attained by the Weierstrass extreme value theorem
Extreme value theorem
In calculus, the extreme value theorem states that if a real-valued function f is continuous in the closed and bounded interval [a,b], then f must attain its maximum and minimum value, each at least once...
, so we can replace the supremum by the maximum. In this case, the norm is also called the maximum norm.
The space is complete under this norm, and the resulting Banach space is denoted by C[a, b]. This example can be generalized to the space C(X) of all continuous functions X → K, where X is a compact space
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, or to the space of all bounded continuous functions X → K, where X is any topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, or indeed to the space B(X) of all bounded functions X → K, where X is any set. In all these examples, we can even multiply functions and stay in the same space: all these examples are in fact unital Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
s.
For any open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
Ω ⊆ C, the set A(Ω) of all bounded, analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s u : Ω → C is a complex Banach space with respect to the supremum norm. The fact that uniform limits of analytic functions are analytic is an easy consequence of Morera's theorem
Morera's theorem
In complex analysis, a branch of mathematics, Morera's theorem, named after Giacinto Morera, gives an important criterion for proving that a function is holomorphic....
.
If p ≥ 0 is a real number, we can consider the space of all infinite sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s (x1, x2, x3, …) of elements in K such that the infinite series ∑i |xi|p is finite. The p-th root of this series' value is then defined to be the p-norm of the sequence. The space, together with this norm, is a Banach space; it is denoted by ℓ p.
The Banach space ℓ∞ consists of all bounded sequences of elements in K; the norm of such a sequence is defined to be the supremum of the absolute values of the sequence's members.
Again, if p ≥ 1 is a real number, we can consider all functions ƒ : [a, b] → K such that |ƒ|p is Lebesgue integrable
Lebesgue integration
In mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
. The p-th root of this integral is then defined to be the norm of ƒ. By itself, this space is not a Banach space because there are non-zero functions whose norm is zero. We define an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
as follows: ƒ and g are equivalent if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the norm of ƒ−g is zero. The set of equivalence classes then forms a Banach space; it is denoted by Lp([a, b]). It is crucial to use the Lebesgue integral and not the Riemann integral here, because the Riemann integral would not yield a complete space. These examples can be generalized; see Lp spaces
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
for details.
If X and Y are two Banach spaces, then we can form their direct sum X ⊕ Y, which has a natural topological vector space structure but no canonical norm. However, it is again a Banach space for several equivalent norms, for example
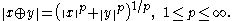
This construction can be generalized to define ℓp-direct sums of arbitrarily many Banach spaces. When there is an infinite number of non-zero summands, the space obtained in this way depends upon p.
If M is a closed linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of the Banach space X, then the quotient space
Quotient space (linear algebra)
In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
X / M is again a Banach space.
Every inner product gives rise to an associated norm. The inner product space is called a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
if its associated norm is complete. Thus every Hilbert space is a Banach space by definition. The converse statement also holds under certain conditions; see below.
Linear operators
If V and W are Banach spaces over the same ground field K, the set of all continuousK-linear maps
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
A : V → W
is denoted by L(V, W). In infinite-dimensional spaces, not all linear maps are automatically continuous. In general, a linear mapping on a normed space is continuous if and only if it is bounded
Bounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
on the closed unit ball. Thus the vector space L(V, W) can be given the operator norm
Operator norm
In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
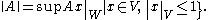
With respect to this norm, L(V,W) is a Banach space. This is also true under the less restrictive condition that V be a normed space.
When V = W, the space L(V) = L(V, V) forms a unital Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
; the multiplication operation is given by the composition of linear maps.
Dual space
If V is a Banach space and K is the underlying fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
(either the real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or the complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
numbers), then K is itself a Banach space (using the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
as norm) and we can define the dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
V
Operator norm
In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
). It can be used to define a new topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
on V: the weak topology
Weak topology
In mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
.
Note that the requirement that the maps be continuous is essential; if V is infinite-dimensional, there exist linear maps which are not continuous, and therefore not bounded
Bounded function
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
, so the space V∗ of linear maps into K is not a Banach space. The space V∗ (which may be called the algebraic dual space to distinguish it from V
There is a natural map F from V to V
- F(x)(ƒ) = ƒ(x)
for all x in V and ƒ in V
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
, this map is injective, and isometric; if it is also surjective, then the Banach space V is called reflexive
Reflexive space
In functional analysis, a Banach space is called reflexive if it coincides with the dual of its dual space in the topological and algebraic senses. Reflexive Banach spaces are often characterized by their geometric properties.- Normed spaces :Suppose X is a normed vector space over R or C...
. Reflexive spaces have many important geometric properties. A space is reflexive if and only if its dual is reflexive, which is the case if and only if its unit ball is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
in the weak topology
Weak topology
In mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
.
For example, ℓp is reflexive for 1 < p < ∞ but ℓ1 and ℓ∞ are not reflexive. When p < ∞, the dual of ℓp is ℓq where p and q are related by the formula 1/p + 1/q = 1. See L p spaces
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
for details.
Relationship to Hilbert spaces
As mentioned above, every Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
is a Banach space because, by definition, a Hilbert space is complete with respect to the norm associated with its inner product, where a norm and an inner product are said to be associated if ||v||² = (v,v) for all v.
The converse is not always true; not every Banach space is a Hilbert space. A necessary and sufficient condition for a Banach space V to be associated to an inner product (which will then necessarily make V into a Hilbert space) is the parallelogram identity:

for all u and v in V, and where ||*|| is the norm on V. So, for example, while Rn is a Banach space with respect to any norm defined on it, it is only a Hilbert space with respect to the Euclidean norm. Similarly, as an infinite-dimensional example, the Lebesgue space Lp is always a Banach space but is only a Hilbert space when p = 2.
If the norm of a Banach space satisfies this identity, the associated inner product which makes it into a Hilbert space is given by the polarization identity
Polarization identity
In mathematics, the polarization identity is any one of a family of formulas that express the inner product of two vectors in terms of the norm of a normed vector space. Let \|x\| \, denote the norm of vector x and \langle x, \ y \rangle \, the inner product of vectors x and y...
. If V is a real Banach space, then the polarization identity is
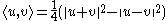
whereas if V is a complex Banach space, then the polarization identity is given by (assuming that scalar product is linear in first argument):
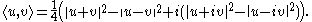
The necessity of this condition follows easily from the properties of an inner product. To see that it is sufficient—that the parallelogram law implies that the form defined by the polarization identity is indeed a complete inner product—one verifies algebraically that this form is additive, whence it follows by induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
that the form is linear over the integers and rationals. Then since every real is the limit of some Cauchy sequence of rationals, the completeness of the norm extends the linearity to the whole real line. In the complex case, one can check also that the bilinear form is linear over i in one argument, and conjugate linear in the other.
Hamel dimension
It follows from the completeness of Banach spaces and the Baire category theoremBaire category theorem
The Baire category theorem is an important tool in general topology and functional analysis. The theorem has two forms, each of which gives sufficient conditions for a topological space to be a Baire space....
that a Hamel basis of an infinite-dimensional Banach space is uncountable.
Derivatives
Several concepts of a derivative may be defined on a Banach space. See the articles on the Fréchet derivativeFréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
and the Gâteaux derivative
Gâteaux derivative
In mathematics, the Gâteaux differential or Gâteaux derivative is a generalization of the concept of directional derivative in differential calculus. Named after René Gâteaux, a French mathematician who died young in World War I, it is defined for functions between locally convex topological vector...
.
Generalizations
Several important spaces in functional analysis, for instance the space of all infinitely often differentiable functions R → R or the space of all distributionsDistribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
on R, are complete but are not normed vector spaces and hence not Banach spaces. In Fréchet space
Fréchet space
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
s one still has a complete metric
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, while LF-space
LF-space
In mathematics, an LF-space is a topological vector space V that is a countable strict inductive limit of Fréchet spaces. This means that for each n there is a subspace V_n such that-Properties:...
s are complete uniform
Uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
vector spaces arising as limits of Fréchet spaces.
See also
- List of Banach spaces
- Cantor–Bernstein–Schroeder theoremCantor–Bernstein–Schroeder theoremIn set theory, the Cantor–Bernstein–Schroeder theorem, named after Georg Cantor, Felix Bernstein, and Ernst Schröder, states that, if there exist injective functions and between the sets A and B, then there exists a bijective function...
- Space (mathematics)

