Distance
Encyclopedia
Distance is a numerical description of how far apart objects are. In physics
or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria (e.g. "two counties over"). In mathematics
, a distance function or metric
is a generalization of the concept of physical distance. A metric is a function that behaves according to a specific set of rules, and provides a concrete way of describing what it means for elements of some space to be "close to" or "far away from" each other.
In most cases, "distance from A to B" is interchangeable with "distance between B and A".
between them:

In analytic geometry
, the distance between two points of the xy-plane
can be found using the distance formula. The distance between (x1, y1) and (x2, y2) is given by:
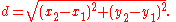
Similarly, given points (x1, y1, z1) and (x2, y2, z2) in three-space
, the distance between them is:

These formulae are easily derived by constructing a right triangle with a leg on the hypotenuse
of another (with the other leg orthogonal to the plane
that contains the 1st triangle) and applying the Pythagorean theorem
.
In the study of complicated geometries, we call this (most common) type of distance Euclidean distance
, as it is derived from the Pythagorean theorem
, which does not hold in Non-Euclidean geometries
. This distance formula
can also be expanded into the arc-length formula
.
Rn, the distance between two points is usually given by the Euclidean distance
(2-norm distance). Other distances, based on other norms
, are sometimes used instead.
For a point (x1, x2, ...,xn) and a point (y1, y2, ...,yn), the Minkowski distance
of order p (p-norm distance) is defined as:
p need not be an integer, but it cannot be less than 1, because otherwise the triangle inequality
does not hold.
The 2-norm distance is the Euclidean distance
, a generalization of the Pythagorean theorem
to more than two coordinates. It is what would be obtained if the distance between two points were measured with a ruler
: the "intuitive" idea of distance.
The 1-norm distance is more colourfully called the taxicab norm or Manhattan distance
, because it is the distance a car would drive in a city laid out in square blocks (if there are no one-way streets).
The infinity norm distance is also called Chebyshev distance
. In 2D, it is the minimum number of moves king
s require to travel between two squares on a chessboard
.
The p-norm is rarely used for values of p other than 1, 2, and infinity, but see super ellipse.
In physical space the Euclidean distance is in a way the most natural one, because in this case the length of a rigid body
does not change with rotation
.
 and
and  ) may be written in a variational
) may be written in a variational
form where the distance is the minimum value of an integral:
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria (e.g. "two counties over"). In mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a distance function or metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
is a generalization of the concept of physical distance. A metric is a function that behaves according to a specific set of rules, and provides a concrete way of describing what it means for elements of some space to be "close to" or "far away from" each other.
In most cases, "distance from A to B" is interchangeable with "distance between B and A".
Geometry
In neutral geometry, the distance between (x1) and (x2) is the length of the line segmentLine (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
between them:

In analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
, the distance between two points of the xy-plane
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
can be found using the distance formula. The distance between (x1, y1) and (x2, y2) is given by:
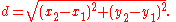
Similarly, given points (x1, y1, z1) and (x2, y2, z2) in three-space
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
, the distance between them is:

These formulae are easily derived by constructing a right triangle with a leg on the hypotenuse
Hypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...
of another (with the other leg orthogonal to the plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
that contains the 1st triangle) and applying the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
.
In the study of complicated geometries, we call this (most common) type of distance Euclidean distance
Euclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
, as it is derived from the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
, which does not hold in Non-Euclidean geometries
Non-Euclidean geometry
Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
. This distance formula
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
can also be expanded into the arc-length formula
Arc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
.
Distance in Euclidean space
In the Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn, the distance between two points is usually given by the Euclidean distance
Euclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
(2-norm distance). Other distances, based on other norms
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
, are sometimes used instead.
For a point (x1, x2, ...,xn) and a point (y1, y2, ...,yn), the Minkowski distance
Minkowski distance
The Minkowski distance is a metric on Euclidean space which can be considered as a generalization of both the Euclidean distance and the Manhattan distance.-Definition:The Minkowski distance of order p between two pointsis defined as:...
of order p (p-norm distance) is defined as:
| 1-norm distance | |
| 2-norm distance | |
| p-norm distance | |
| infinity norm distance | |
p need not be an integer, but it cannot be less than 1, because otherwise the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
does not hold.
The 2-norm distance is the Euclidean distance
Euclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
, a generalization of the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
to more than two coordinates. It is what would be obtained if the distance between two points were measured with a ruler
Ruler
A ruler, sometimes called a rule or line gauge, is an instrument used in geometry, technical drawing, printing and engineering/building to measure distances and/or to rule straight lines...
: the "intuitive" idea of distance.
The 1-norm distance is more colourfully called the taxicab norm or Manhattan distance
Taxicab geometry
Taxicab geometry, considered by Hermann Minkowski in the 19th century, is a form of geometry in which the usual distance function or metric of Euclidean geometry is replaced by a new metric in which the distance between two points is the sum of the absolute differences of their coordinates...
, because it is the distance a car would drive in a city laid out in square blocks (if there are no one-way streets).
The infinity norm distance is also called Chebyshev distance
Chebyshev distance
In mathematics, Chebyshev distance , Maximum metric, or L∞ metric is a metric defined on a vector space where the distance between two vectors is the greatest of their differences along any coordinate dimension...
. In 2D, it is the minimum number of moves king
King (chess)
In chess, the king is the most important piece. The object of the game is to trap the opponent's king so that its escape is not possible . If a player's king is threatened with capture, it is said to be in check, and the player must remove the threat of capture on the next move. If this cannot be...
s require to travel between two squares on a chessboard
Chessboard
A chessboard is the type of checkerboard used in the board game chess, and consists of 64 squares arranged in two alternating colors...
.
The p-norm is rarely used for values of p other than 1, 2, and infinity, but see super ellipse.
In physical space the Euclidean distance is in a way the most natural one, because in this case the length of a rigid body
Rigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
does not change with rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
.
Variational formulation of distance
The Euclidean distance between two points in space ( and
and 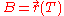 ) may be written in a variational
) may be written in a variationalCalculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
form where the distance is the minimum value of an integral:
-

Here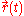 is the trajectory (path) between the two points. The value of the integral (D) represents the length of this trajectory. The distance is the minimal value of this integral and is obtained when
is the trajectory (path) between the two points. The value of the integral (D) represents the length of this trajectory. The distance is the minimal value of this integral and is obtained when  where
where  is the optimal trajectory. In the familiar Euclidean case (the above integral) this optimal trajectory is simply a straight line. It is well known that the shortest path between two points is a straight line. Straight lines can formally be obtained by solving the Euler-Lagrange equations for the above functionalFunctional (mathematics)In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
is the optimal trajectory. In the familiar Euclidean case (the above integral) this optimal trajectory is simply a straight line. It is well known that the shortest path between two points is a straight line. Straight lines can formally be obtained by solving the Euler-Lagrange equations for the above functionalFunctional (mathematics)In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
. In non-EuclideanNon-Euclidean geometryNon-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
manifolds (curved spaces) where the nature of the space is represented by a metricMetric (mathematics)In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
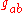 the integrand has be to modified to
the integrand has be to modified to 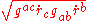 , where Einstein summation convention has been used.
, where Einstein summation convention has been used.
Generalization to higher-dimensional objects
The Euclidean distance between two objects may also be generalized to the case where the objects are no longer points but are higher-dimensional manifolds, such as space curves, so in addition to talking about distance between two points one can discuss concepts of distance between two strings. Since the new objects that are dealt with are extended objects (not points anymore) additional concepts such as non-extensibility, curvatureCurvatureIn mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
constraints, and non-local interactions that enforce non-crossing become central to the notion of distance. The distance between the two manifolds is the scalar quantity that results from minimizing the generalized distance functional, which represents a transformation between the two manifolds:
-

The above double integral is the generalized distance functional between two plymer conformation. is a spatial parameter and
is a spatial parameter and  is pseudo-time. This means that
is pseudo-time. This means that 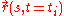 is the polymer/string conformation at time
is the polymer/string conformation at time 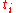 and is parameterized along the string length by
and is parameterized along the string length by  . Similarly
. Similarly 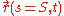 is the trajectory of an infinitesimal segment of the string during transformation of the entire string from conformation
is the trajectory of an infinitesimal segment of the string during transformation of the entire string from conformation 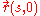 to conformation
to conformation 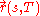 . The term with cofactor
. The term with cofactor 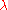 is a Lagrange multiplier and its role is to ensure that the length of the polymer remains the same during the transformation. If two discrete polymers are inextensible, then the minimal-distance transformation between them no longer involves purely straight-line motion, even on a Euclidean metric. There is a potential application of such generalized distance to the problem of protein foldingProtein foldingProtein folding is the process by which a protein structure assumes its functional shape or conformation. It is the physical process by which a polypeptide folds into its characteristic and functional three-dimensional structure from random coil....
is a Lagrange multiplier and its role is to ensure that the length of the polymer remains the same during the transformation. If two discrete polymers are inextensible, then the minimal-distance transformation between them no longer involves purely straight-line motion, even on a Euclidean metric. There is a potential application of such generalized distance to the problem of protein foldingProtein foldingProtein folding is the process by which a protein structure assumes its functional shape or conformation. It is the physical process by which a polypeptide folds into its characteristic and functional three-dimensional structure from random coil....
This generalized distance is analogous to the Nambu-Goto actionNambu-Goto actionThe Nambu–Goto action is the simplest invariant action in bosonic string theory, and is also used in other theories that investigate string-like objects . It is the starting point of the analysis of zero-thickness string behavior, using the principles of Lagrangian mechanics...
in string theoryString theoryString theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, however there is no exact correspondence because the Euclidean distance in 3-space is inequivalent to the space-time distance minimized for the classical relativistic string.
Algebraic distance
The algebraic distance is a metric often used in computer visionComputer visionComputer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
that can be minimized by least squaresLeast squaresThe method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
estimation. http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/FISHER/ALGDIST/alg.htmhttp://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/FISHER/CIRCLEFIT/fit2dcircle/node3.html For curves or surfaces given by the equation (such as a conic in homogeneous coordinates), the algebraic distance from the point
(such as a conic in homogeneous coordinates), the algebraic distance from the point 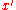 to the curve is simply
to the curve is simply  .
.
It may serve as an "initial guess" for geometric distance to refine estimations of the curve by more accurate methods, such as non-linear least squaresNon-linear least squaresNon-linear least squares is the form of least squares analysis which is used to fit a set of m observations with a model that is non-linear in n unknown parameters . It is used in some forms of non-linear regression. The basis of the method is to approximate the model by a linear one and to...
.
General case
In mathematicsMathematicsMathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in particular geometryGeometryGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a distance functionMetric (mathematics)In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
on a given set M is a functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
d: M×M → R, where R denotes the set of real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, that satisfies the following conditions:- d(x,y) ≥ 0, and d(x,y) = 0 if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
x = y. (Distance is positive between two different points, and is zero precisely from a point to itself.) - It is symmetricSymmetric relationIn mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
: d(x,y) = d(y,x). (The distance between x and y is the same in either direction.) - It satisfies the triangle inequalityTriangle inequalityIn mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
: d(x,z) ≤ d(x,y) + d(y,z). (The distance between two points is the shortest distance along any path).
Such a distance function is known as a metricMetric (mathematics)In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
. Together with the set, it makes up a metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
.
For example, the usual definition of distance between two real numbers x and y is: d(x,y) = |x − y|. This definition satisfies the three conditions above, and corresponds to the standard topologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
of the real lineReal lineIn mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
. But distance on a given set is a definitional choice. Another possible choice is to define: d(x,y) = 0 if x = y, and 1 otherwise. This also defines a metric, but gives a completely different topology, the "discrete topology"; with this definition numbers cannot be arbitrarily close.
Distances between sets and between a point and a set
Various distance definitions are possible between objects. For example, between celestial bodies one should not confuse the surface-to-surface distance and the center-to-center distance. If the former is much less than the latter, as for a LEOLow Earth orbitA low Earth orbit is generally defined as an orbit within the locus extending from the Earth’s surface up to an altitude of 2,000 km...
, the first tends to be quoted (altitude), otherwise, e.g. for the Earth-Moon distance, the latter.
There are two common definitions for the distance between two non-empty subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of a given set:- One version of distance between two non-empty sets is the infimumInfimumIn mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of the distances between any two of their respective points, which is the every-day meaning of the word. This is a symmetric premetric. On a collection of sets of which some touch or overlap each other, it is not "separating", because the distance between two different but touching or overlapping sets is zero. Also it is not hemimetric, i.e., the triangle inequalityTriangle inequalityIn mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
does not hold, except in special cases. Therefore only in special cases this distance makes a collection of sets a metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
. - The Hausdorff distanceHausdorff distanceIn mathematics, the Hausdorff distance, or Hausdorff metric, also called Pompeiu–Hausdorff distance, measures how far two subsets of a metric space are from each other. It turns the set of non-empty compact subsets of a metric space into a metric space in its own right...
is the larger of two values, one being the supremumSupremumIn mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
, for a point ranging over one set, of the infimum, for a second point ranging over the other set, of the distance between the points, and the other value being likewise defined but with the roles of the two sets swapped. This distance makes the set of non-empty compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
subsets of a metric space itself a metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
.
The distance between a point and a set is the infimum of the distances between the point and those in the set. This corresponds to the distance, according to the first-mentioned definition above of the distance between sets, from the set containing only this point to the other set.
In terms of this, the definition of the Hausdorff distance can be simplified: it is the larger of two values, one being the supremum, for a point ranging over one set, of the distance between the point and the set, and the other value being likewise defined but with the roles of the two sets swapped.
Graph theory
In graph theoryGraph theoryIn mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
the distance between two vertices is the length of the shortest pathPath (graph theory)In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...
between those vertices.
Distance versus directed distance and displacement
Distance cannot be negative and distance travelled never decreases. Distance is a scalar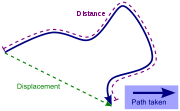 Scalar (physics)In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
Scalar (physics)In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
quantity or a magnitudeMagnitude (mathematics)The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....
, whereas displacementDisplacement (vector)A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
is a vector quantity with both magnitude and directionDirection (geometry, geography)Direction is the information contained in the relative position of one point with respect to another point without the distance information. Directions may be either relative to some indicated reference , or absolute according to some previously agreed upon frame of reference Direction is the...
.
The distance covered by a vehicle (for example as recorded by an odometerOdometerAn odometer or odograph is an instrument that indicates distance traveled by a vehicle, such as a bicycle or automobile. The device may be electronic, mechanical, or a combination of the two. The word derives from the Greek words hodós and métron...
), person, animal, or object along a curved path from a point A to a point B should be distinguished from the straight line distance from A to B. For example whatever the distance covered during a round trip from A to B and back to A, the displacement is zero as start and end points coincide. In general the straight line distance does not equal distance travelled, except for journeys in a straight line.
Directed distance
Directed distances are distances with a direction or sense. They can be determined along straight lines and along curved lines. A directed distance along a straight line from A to B is a vector joining any two points in a n-dimensional Euclidean vector space. A directed distance along a curved line is not a vector and is represented by a segment of that curved line defined by endpoints A and B, with some specific information indicating the sense (or direction) of an ideal or real motion from one endpoint of the segment to the other (see figure). For instance, just labelling the two endpoints as A and B can indicate the sense, if the ordered sequence (A, B) is assumed, which implies that A is the starting point.
A displacement (see above) is a special kind of directed distance defined in mechanicsMechanicsMechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
. A directed distance is called displacement when it is the distance along a straight line (minimum distance) from A and B, and when A and B are positions occupied by the same particle at two different instants of time. This implies motionMotion (physics)In physics, motion is a change in position of an object with respect to time. Change in action is the result of an unbalanced force. Motion is typically described in terms of velocity, acceleration, displacement and time . An object's velocity cannot change unless it is acted upon by a force, as...
of the particle. displace is a vector quantity.
Another kind of directed distance is that between two different particles or point masses at a given time. For instance, the distance from the center of gravityCenter of gravityIn physics, a center of gravity of a material body is a point that may be used for a summary description of gravitational interactions. In a uniform gravitational field, the center of mass serves as the center of gravity...
of the Earth A and the center of gravityCenter of gravityIn physics, a center of gravity of a material body is a point that may be used for a summary description of gravitational interactions. In a uniform gravitational field, the center of mass serves as the center of gravity...
of the Moon B (which does not strictly imply motion from A to B).Shortest path length may be equal to displacement or may not be equal to.Distance from starting point is always equal to magnitude of displacement.
For same particle distance travelled is always greater than or equal to magnitude of displacement. Shortest path length is not necessary always displacement.Diplacement may increase or decrease but distance travelled never decreases.
Other "distances"
- E-statistics, or energy statistics, are functions of distances between statistical observations.
- Mahalanobis distanceMahalanobis distanceIn statistics, Mahalanobis distance is a distance measure introduced by P. C. Mahalanobis in 1936. It is based on correlations between variables by which different patterns can be identified and analyzed. It gauges similarity of an unknown sample set to a known one. It differs from Euclidean...
is used in statisticsStatisticsStatistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
. - Hamming distanceHamming distanceIn information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
and Lee distance are used in coding theoryCoding theoryCoding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
. - Levenshtein distanceLevenshtein distanceIn information theory and computer science, the Levenshtein distance is a string metric for measuring the amount of difference between two sequences...
- Chebyshev distanceChebyshev distanceIn mathematics, Chebyshev distance , Maximum metric, or L∞ metric is a metric defined on a vector space where the distance between two vectors is the greatest of their differences along any coordinate dimension...
- Canberra distanceCanberra distanceThe Canberra distance is a numerical measure of the distance between pairs of points in a vector space, introduced in 1966and refined in 1967 by G. N. Lance and W. T. Williams. It is similar to the Manhattan distance...
Circular distance is the distance traveled by a wheel. The circumference of the wheel is 2π × radius, and assuming the radius to be 1, then each revolution of the wheel is equivalent of the distance 2π radians. In engineering ω = 2πƒ is often used, where ƒ is the frequency.
See also
- Taxicab geometryTaxicab geometryTaxicab geometry, considered by Hermann Minkowski in the 19th century, is a form of geometry in which the usual distance function or metric of Euclidean geometry is replaced by a new metric in which the distance between two points is the sum of the absolute differences of their coordinates...
- Astronomical units of lengthAstronomical units of lengthThe astronomical system of units, formally called the IAU System of Astronomical Constants, is a system of measurement developed for use in astronomy...
- Cosmic distance ladderCosmic distance ladderThe cosmic distance ladder is the succession of methods by which astronomers determine the distances to celestial objects. A real direct distance measurement of an astronomical object is possible only for those objects that are "close enough" to Earth...
- Distance measures (cosmology)Distance measures (cosmology)Distance measures are used in physical cosmology to give a natural notion of the distance between two objects or events in the universe. They are often used to tie some observable quantity to another quantity that is not directly...
- Comoving distanceComoving distanceIn standard cosmology, comoving distance and proper distance are two closely related distance measures used by cosmologists to define distances between objects...
- Distance geometryDistance geometryDistance geometry is the characterization and study of sets of points based only on given values of the distances between member pairs. Therefore distance geometry has immediate relevance where distance values are determined or considered, such as in surveying, cartography and...
- Distance (graph theory)Distance (graph theory)In the mathematical field of graph theory, the distance between two vertices in a graph is the number of edges in a shortest path connecting them. This is also known as the geodesic distance...
- Dijkstra's algorithmDijkstra's algorithmDijkstra's algorithm, conceived by Dutch computer scientist Edsger Dijkstra in 1956 and published in 1959, is a graph search algorithm that solves the single-source shortest path problem for a graph with nonnegative edge path costs, producing a shortest path tree...
- Distance-based road exit numbers
- Distance measuring equipmentDistance Measuring EquipmentDistance measuring equipment is a transponder-based radio navigation technology that measures distance by timing the propagation delay of VHF or UHF radio signals....
(DME) - Engineering tolerance
- Great-circle distanceGreat-circle distanceThe great-circle distance or orthodromic distance is the shortest distance between any two points on the surface of a sphere measured along a path on the surface of the sphere . Because spherical geometry is rather different from ordinary Euclidean geometry, the equations for distance take on a...
- LengthLengthIn geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
- MilestoneMilestoneA milestone is one of a series of numbered markers placed along a road or boundary at intervals of one mile or occasionally, parts of a mile. They are typically located at the side of the road or in a median. They are alternatively known as mile markers, mileposts or mile posts...
- Metric (mathematics)Metric (mathematics)In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
- Metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
- Orders of magnitude (length)
- Proper lengthProper lengthIn relativistic physics, proper length is an invariant measure of the distance between two spacelike-separated events, or of the length of a spacelike path within a spacetime....
- Distance matrixDistance matrixIn mathematics, computer science and graph theory, a distance matrix is a matrix containing the distances, taken pairwise, of a set of points...
- Hamming distanceHamming distanceIn information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
- Lee distance
- ProxemicsProxemicsProxemics is the study of measurable distances between people as they interact. The term was introduced by anthropologist Edward T. Hall in 1966...
– physical distance between people - Meridian arcMeridian arcIn geodesy, a meridian arc measurement is a highly accurate determination of the distance between two points with the same longitude. Two or more such determinations at different locations then specify the shape of the reference ellipsoid which best approximates the shape of the geoid. This...
- d(x,y) ≥ 0, and d(x,y) = 0 if and only if
-

