
Topological space
Encyclopedia

Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
, connectedness
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, and continuity. They appear in virtually every branch of modern mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and are a central unifying notion. The branch of mathematics that studies topological spaces in their own right is called topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
.
Definition
A topological space is a set X together with (a collection of subset
(a collection of subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of X) satisfying the following axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s:
- The empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
and X are in .
. -
 is closed underClosure (mathematics)In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
is closed underClosure (mathematics)In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
arbitrary unionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
. -
 is closed under finite intersectionIntersection (set theory)In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
is closed under finite intersectionIntersection (set theory)In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
.
The collection
 is called a topology on X. The elements of X are usually called points, though they can be any mathematical objects. A topological space in which the points are functions is called a function space
is called a topology on X. The elements of X are usually called points, though they can be any mathematical objects. A topological space in which the points are functions is called a function spaceFunction space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
. The sets in
 are called the open set
are called the open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s, and their complements
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
in X are called closed set
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
s. A subset of X may be neither closed nor open, either closed or open, or both. A set that is both closed and open is called a clopen set
Clopen set
In topology, a clopen set in a topological space is a set which is both open and closed. That this is possible for a set is not as counter-intuitive as it might seem if the terms open and closed were thought of as antonyms; in fact they are not...
.
Examples
- X = {1, 2, 3, 4} and collection
 = of only the two subsets of X required by the axioms form a topology, the trivial topologyTrivial topologyIn topology, a topological space with the trivial topology is one where the only open sets are the empty set and the entire space. Such a space is sometimes called an indiscrete space, and its topology sometimes called an indiscrete topology...
= of only the two subsets of X required by the axioms form a topology, the trivial topologyTrivial topologyIn topology, a topological space with the trivial topology is one where the only open sets are the empty set and the entire space. Such a space is sometimes called an indiscrete space, and its topology sometimes called an indiscrete topology...
(indiscrete topology). - X = {1, 2, 3, 4} and collection
 = of six subsets of X form another topology.
= of six subsets of X form another topology. - X = {1, 2, 3, 4} and collection
 = P(X) (the power set of X) form a third topology, the discrete topology.
= P(X) (the power set of X) form a third topology, the discrete topology. - X = Z, the set of integers, and collection
 equal to all finite subsets of the integers plus Z itself is not a topology, because (for example) the union of all finite sets not containing zero is infinite but is not all of Z, and so is not in
equal to all finite subsets of the integers plus Z itself is not a topology, because (for example) the union of all finite sets not containing zero is infinite but is not all of Z, and so is not in  .
.
Equivalent definitions
There are many other equivalent ways to define a topological space. (In other words, each of the following defines a categoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
equivalent to the category of topological spaces above.) For example, using de Morgan's laws, the axioms defining open sets above become axioms defining closed sets:
- The empty set and X are closed.
- The intersection of any collection of closed sets is also closed.
- The union of any pair of closed sets is also closed.
Using these axioms, another way to define a topological space is as a set X together with a collection
 of subsets of X satisfying the following axioms:
of subsets of X satisfying the following axioms:- The empty set and X are in
 .
. - The intersection of any collection of sets in
 is also in
is also in  .
. - The union of any pair of sets in
 is also in
is also in  .
.
Under this definition, the sets in the topology
 are the closed sets, and their complements in X are the open sets.
are the closed sets, and their complements in X are the open sets.Another way to define a topological space is by using the Kuratowski closure axioms
Kuratowski closure axioms
In topology and related branches of mathematics, the Kuratowski closure axioms are a set of axioms which can be used to define a topological structure on a set. They are equivalent to the more commonly used open set definition...
, which define the closed sets as the fixed points of an operator on the power set of X.
A neighbourhood of a point x is any set that has an open subset containing x. The neighbourhood system at x consists of all neighbourhoods of x. A topology can be determined by a set of axioms concerning all neighbourhood systems.
A net
Net (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
is a generalisation of the concept of sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
. A topology is completely determined if for every net in X the set of its accumulation point
Topology glossary
This is a glossary of some terms used in the branch of mathematics known as topology. Although there is no absolute distinction between different areas of topology, the focus here is on general topology...
s is specified.
Comparison of topologies
A variety of topologies can be placed on a set to form a topological space. When every set in a topology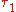 is also in a topology
is also in a topology  , we say that
, we say that 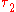 is finer than
is finer than 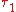 , and
, and 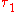 is coarser than
is coarser than 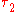 . A proof that relies only on the existence of certain open sets will also hold for any finer topology, and similarly a proof that relies only on certain sets not being open applies to any coarser topology. The terms larger and smaller are sometimes used in place of finer and coarser, respectively. The terms stronger and weaker are also used in the literature, but with little agreement on the meaning, so one should always be sure of an author's convention when reading.
. A proof that relies only on the existence of certain open sets will also hold for any finer topology, and similarly a proof that relies only on certain sets not being open applies to any coarser topology. The terms larger and smaller are sometimes used in place of finer and coarser, respectively. The terms stronger and weaker are also used in the literature, but with little agreement on the meaning, so one should always be sure of an author's convention when reading.The collection of all topologies on a given fixed set X forms a complete lattice
Complete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
: if F = {
 :
:  in A} is a collection of topologies on X, then the meet of F is the intersection of F, and the join of F is the meet of the collection of all topologies on X that contain every member of F.
in A} is a collection of topologies on X, then the meet of F is the intersection of F, and the join of F is the meet of the collection of all topologies on X that contain every member of F.Continuous functions
A functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
between topological spaces is called continuous if the inverse image of every open set is open. This is an attempt to capture the intuition that there are no "breaks" or "separations" in the function. A homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
is a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
that is continuous and whose inverse
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
is also continuous. Two spaces are called homeomorphic if there exists a homeomorphism between them. From the standpoint of topology, homeomorphic spaces are essentially identical.
In category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, Top, the category of topological spaces
Category of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
with topological spaces as objects and continuous functions as morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s is one of the fundamental categories
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
in mathematics. The attempt to classify the objects of this category (up to homeomorphism) by invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
s has motivated and generated entire areas of research, such as homotopy theory
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
, homology theory
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
, and K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
, to name just a few.
Examples of topological spaces
A given set may have many different topologies. If a set is given a different topology, it is viewed as a different topological space. Any set can be given the discrete topologyDiscrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
in which every subset is open. The only convergent sequences or nets in this topology are those that are eventually constant. Also, any set can be given the trivial topology
Trivial topology
In topology, a topological space with the trivial topology is one where the only open sets are the empty set and the entire space. Such a space is sometimes called an indiscrete space, and its topology sometimes called an indiscrete topology...
(also called the indiscrete topology), in which only the empty set and the whole space are open. Every sequence and net in this topology converges to every point of the space. This example shows that in general topological spaces, limits of sequences need not be unique. However, often topological spaces must be Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
s where limit points are unique.
There are many ways of defining a topology on R, the set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. The standard topology on R is generated by the open intervals. The set of all open intervals forms a base
Base (topology)
In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
or basis for the topology, meaning that every open set is a union of some collection of sets from the base. In particular, this means that a set is open if there exists an open interval of non zero radius about every point in the set. More generally, the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s Rn can be given a topology. In the usual topology on Rn the basic open sets are the open ball
Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
s. Similarly, C and Cn have a standard topology in which the basic open sets are open balls.
Every metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
can be given a metric topology, in which the basic open sets are open balls defined by the metric. This is the standard topology on any normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
. On a finite-dimensional vector space this topology is the same for all norms.
Many sets of linear operators in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
are endowed with topologies that are defined by specifying when a particular sequence of functions converges to the zero function.
Any local field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
has a topology native to it, and this can be extended to vector spaces over that field.
Every manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
has a natural topology since it is locally Euclidean. Similarly, every simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
and every simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
inherits a natural topology from Rn.
The Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
is defined algebraically on the spectrum of a ring
Spectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
or an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
. On Rn or Cn, the closed sets of the Zariski topology are the solution sets of systems of polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
equations.
A linear graph has a natural topology that generalises many of the geometric aspects of graph
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
s with vertices and edges.
The Sierpiński space
Sierpinski space
In mathematics, the Sierpiński space is a finite topological space with two points, only one of which is closed.It is the smallest example of a topological space which is neither trivial nor discrete...
is the simplest non-discrete topological space. It has important relations to the theory of computation and semantics.
There exist numerous topologies on any given finite set. Such spaces are called finite topological space
Finite topological space
In mathematics, a finite topological space is a topological space for which the underlying point set is finite. That is, it is a topological space for which there are only finitely many points....
s. Finite spaces are sometimes used to provide examples or counterexamples to conjectures about topological spaces in general.
Any set can be given the cofinite topology in which the open sets are the empty set and the sets whose complement is finite. This is the smallest T1
T1 space
In topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
topology on any infinite set.
Any set can be given the cocountable topology
Cocountable topology
The cocountable topology or countable complement topology on any set X consists of the empty set and all cocountable subsets of X, that is all sets whose complement in X is countable...
, in which a set is defined as open if it is either empty or its complement is countable. When the set is uncountable, this topology serves as a counterexample in many situations.
The real line can also be given the lower limit topology
Lower limit topology
In mathematics, the lower limit topology or right half-open interval topology is a topology defined on the set R of real numbers; it is different from the standard topology on R and has a number of interesting properties...
. Here, the basic open sets are the half open intervals
If Γ is an ordinal number
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
, then the set Γ = [0, Γ) may be endowed with the order topology
Order topology
In mathematics, an order topology is a certain topology that can be defined on any totally ordered set. It is a natural generalization of the topology of the real numbers to arbitrary totally ordered sets...
generated by the intervals (a, b), [0, b) and (a, Γ) where a and b are elements of Γ.
Topological constructions
Every subset of a topological space can be given the subspace topologySubspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
in which the open sets are the intersections of the open sets of the larger space with the subset. For any indexed family
Indexed family
In mathematics, an indexed family is a collection of values that are associated with indexes. For example, a family of real numbers, indexed by the integers is a collection of real numbers, where each integer is associated with one of the real numbers....
of topological spaces, the product can be given the product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
, which is generated by the inverse images of open sets of the factors under the projection
Projection (mathematics)
Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
mappings. For example, in finite products, a basis for the product topology consists of all products of open sets. For infinite products, there is the additional requirement that in a basic open set, all but finitely many of its projections are the entire space.
A quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
is defined as follows: if X is a topological space and Y is a set, and if f : X → Y is a surjective function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, then the quotient topology on Y is the collection of subsets of Y that have open inverse images under f. In other words, the quotient topology is the finest topology on Y for which f is continuous. A common example of a quotient topology is when an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
is defined on the topological space X. The map f is then the natural projection onto the set of equivalence classes.
The Vietoris topology on the set of all non-empty subsets of a topological space X, named for Leopold Vietoris
Leopold Vietoris
Leopold Vietoris was an Austrian mathematician and a World War I veteran who gained additional fame by becoming a supercentenarian...
, is generated by the following basis: for every n-tuple U1, ..., Un of open sets in X, we construct a basis set consisting of all subsets of the union of the Ui that have non-empty intersections with each Ui.
Classification of topological spaces
Topological spaces can be broadly classified, up toUp to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
homeomorphism, by their topological properties. A topological property is a property of spaces that is invariant under homeomorphisms. To prove that two spaces are not homeomorphic it is sufficient to find a topological property not shared by them. Examples of such properties include connectedness, compactness, and various separation axiom
Separation axiom
In topology and related fields of mathematics, there are several restrictions that one often makes on the kinds of topological spaces that one wishes to consider. Some of these restrictions are given by the separation axioms...
s.
See the article on topological properties for more details and examples.
Topological spaces with algebraic structure
For any algebraic objectsAlgebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
we can introduce the discrete topology, under which the algebraic operations are continuous functions. For any such structure that is not finite, we often have a natural topology compatible with the algebraic operations, in the sense that the algebraic operations are still continuous. This leads to concepts such as topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
s, topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s, topological ring
Topological ring
In mathematics, a topological ring is a ring R which is also a topological space such that both the addition and the multiplication are continuous as mapswhere R × R carries the product topology.- General comments :...
s and local field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
s.
Topological spaces with order structure
- Spectral. A space is spectralSpectral spaceIn mathematics, a spectral space is a topological space which is homeomorphic to the spectrum of a commutative ring.-Definition:Let X be a topological space and let K\circ be the set of allquasi-compact and open subsets of X...
if and only if it is the prime spectrum of a ringSpectrum of a ringIn abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
(HochsterMelvin HochsterMelvin Hochster is an eminent American mathematician, regarded as one of the leading commutative algebraists active today. He is currently the Jack E. McLaughlin Distinguished University Professor of Mathematics at the University of Michigan.Hochster attended Stuyvesant High School, where he was...
theorem).
- Specialization preorder. In a space the specialization (or canonical) preorder is defined by x ≤ y if and only if clKuratowski closure axiomsIn topology and related branches of mathematics, the Kuratowski closure axioms are a set of axioms which can be used to define a topological structure on a set. They are equivalent to the more commonly used open set definition...
{x} ⊆ clKuratowski closure axiomsIn topology and related branches of mathematics, the Kuratowski closure axioms are a set of axioms which can be used to define a topological structure on a set. They are equivalent to the more commonly used open set definition...
{y}.
Specializations and generalizations
The following spaces and algebras are either more specialized or more general than the topological spaces discussed above.- Proximity spaceProximity spaceIn topology, a proximity space is an axiomatization of notions of "nearness" that hold set-to-set, as opposed to the better known point-to-set notions that characterize topological spaces....
s provide a notion of closeness of two sets. - Metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s embody a metricMetric (mathematics)In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
, a precise notion of distance between points. - Uniform spaceUniform spaceIn the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
s axiomatize ordering the distance between distinct points. - Cauchy spaceCauchy spaceIn general topology and analysis, a Cauchy space is a generalization of metric spaces and uniform spaces for which the notion of Cauchy convergence still makes sense. Cauchy spaces were introduced by H. H. Keller in 1968, as an axiomatic tool derived from the idea of a Cauchy filter, in order to...
s axiomatize the ability to test whether a net is CauchyCauchy netIn mathematics, a Cauchy net generalizes the notion of Cauchy sequence to nets defined on uniform spaces.A net is a Cauchy net if for every entourage V there exists γ such that for all α, β ≥ γ, is a member of V. More generally, in a Cauchy space, a net is Cauchy if the filter generated by the...
. Cauchy spaces provide a general setting for studying completionComplete spaceIn mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
s. - Convergence spaces capture some of the features of convergence of filtersFilter (mathematics)In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
. - Grothendieck sites are categoriesCategory (mathematics)In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
with additional data axiomatizing whether a family of arrows covers an object. Sites are a general setting for defining sheavesSheaf (mathematics)In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
.
See also
- Kolmogorov spaceKolmogorov spaceIn topology and related branches of mathematics, a topological space X is a T0 space or Kolmogorov space if for every pair of distinct points of X, at least one of them has an open neighborhood not containing the other. This condition, called the T0 condition, is one of the separation axioms...
(T0) - accessible/Fréchet spaceT1 spaceIn topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
(T1) - Hausdorff spaceHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
(T2) - completely Hausdorff spaceCompletely Hausdorff spaceIn topology, an Urysohn space, or T2½ space, is a topological space in which any two distinct points can be separated by closed neighborhoods. A completely Hausdorff space, or functionally Hausdorff space, is a topological space in which any two distinct points can be separated by a continuous...
and Urysohn space (T2½) - regular spaceRegular spaceIn topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
and regular Hausdorff space (T3) - Tychonoff spaceTychonoff spaceIn topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
and completely regular space (T3½) - normal Hausdorff space (T4)
- completely normal Hausdorff space (T5)
- perfectly normal Hausdorff space (T6)
- Space (mathematics)
- Complete Heyting algebraComplete Heyting algebraIn mathematics, especially in order theory, a complete Heyting algebra is a Heyting algebra which is complete as a lattice. Complete Heyting algebras are the objects of three different categories; the category CHey, the category Loc of locales, and its opposite, the category Frm of frames...
– The system of all open sets of a given topological space ordered by inclusion is a complete Heyting algebra.

