
Cone (linear algebra)
Encyclopedia
In linear algebra
, a (linear) cone is a subset
of a vector space
that is closed under multiplication
by positive scalars
. In other words, a subset C of a real vector space V is a cone if and only if λx belongs to C for any x in C and any positive scalar λ of V (or, more succinctly, if and only if λC = C for any positive scalar λ).
A cone is said to be pointed if it includes the null vector (origin
) 0; otherwise it is said to be blunt. Some authors use "non-negative" instead of "positive" in this definition of "cone", which restricts the term to the pointed cones only.
The definition makes sense for any vector space V which allows the notion of "positive scalar" (i.e., where the ground field is an ordered field
), such as spaces over the rational
, real algebraic
, or (most commonly) real number
s.
The concept can also be extended for any vector space V whose scalar field is a superset of those fields (such as the complex number
s, quaternion
s, etc.), to the extent that such a space can be viewed as a real vector space of higher dimension.
With this definition, the cone of X is pointed or blunt depending on whether X contains the origin 0 or not. If "positive" is replaced by "non-negative" in this definition, then the cone of X will be pointed, for any X.
 (-C)
(-C) 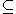 {0}.
{0}.
is a cone that is closed under convex combination
s, i.e. if and only if αx + βy belongs to C for any non-negative scalars α, β with α + β = 1.
then C is said to be an (affine) cone with vertex v. More commonly, in algebraic geometry
, the term affine cone over a projective variety X in PV is the affine variety in V given as the preimage of X under the quotient map
s (set intersection
, union, and complement). They are also closed under addition (if C and D are cones, so is C + D) and arbitrary linear maps. In particular, if C is a cone, so is its opposite cone -C.
for V, with the property that the norm of any vector is a scalar of V. Let S be the unit-norm sphere
of V, that is, the set
By definition, a nonzero vector x belongs to a cone C of V if and only if the unit-norm vector x/|x| belongs to C. Therefore, a blunt (or pointed) cone C is completely specified by its central projection onto S; that is, by the set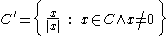
It follows that there is a one-to-one correspondence
between blunt (or pointed) cones and subsets of S.
Indeed, the central projection C' is simply the spherical section of C, the set C S of its unit-norm elements.
S of its unit-norm elements.
A cone C is closed with respect to the norm |·| if it is a closed set in the topology
induced by that norm. That is the case if and only if C is pointed and its spherical section is a closed subset of S.
Note that the cone C is salient if and only if its spherical section does not contain two opposite vectors; that is, C' (-C' ) = {}.
(-C' ) = {}.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a (linear) cone is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
that is closed under multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
by positive scalars
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
. In other words, a subset C of a real vector space V is a cone if and only if λx belongs to C for any x in C and any positive scalar λ of V (or, more succinctly, if and only if λC = C for any positive scalar λ).
A cone is said to be pointed if it includes the null vector (origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
) 0; otherwise it is said to be blunt. Some authors use "non-negative" instead of "positive" in this definition of "cone", which restricts the term to the pointed cones only.
The definition makes sense for any vector space V which allows the notion of "positive scalar" (i.e., where the ground field is an ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
), such as spaces over the rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
, real algebraic
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
, or (most commonly) real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s.
The concept can also be extended for any vector space V whose scalar field is a superset of those fields (such as the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s, etc.), to the extent that such a space can be viewed as a real vector space of higher dimension.
The cone of a set
The (linear) cone of an arbitrary subset X of V is the set X* of all vectors λx where x belongs to X and λ is a positive scalar.With this definition, the cone of X is pointed or blunt depending on whether X contains the origin 0 or not. If "positive" is replaced by "non-negative" in this definition, then the cone of X will be pointed, for any X.
Salient cone
A cone X is said to be salient if it does not contain any pair of opposite nonzero vectors; that is, if and only if C (-C)
(-C) 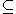 {0}.
{0}.Convex cone
A convex coneConvex cone
In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:...
is a cone that is closed under convex combination
Convex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
s, i.e. if and only if αx + βy belongs to C for any non-negative scalars α, β with α + β = 1.
Affine cone
If C - v is a cone for some v in V,then C is said to be an (affine) cone with vertex v. More commonly, in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, the term affine cone over a projective variety X in PV is the affine variety in V given as the preimage of X under the quotient map

Proper cone
The term proper cone is variously defined, depending on the context. It often means a salient and convex cone, or a cone that is contained in an open halfspace of V.Boolean, additive and linear closure
Linear cones are closed under Boolean operationBoolean operation
Boolean operation or Boolean operator may refer to one of the following related meanings.*Boolean function*an operation in a Boolean algebra; in particular:**operations over the algebra of sets: union , intersection , etc....
s (set intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
, union, and complement). They are also closed under addition (if C and D are cones, so is C + D) and arbitrary linear maps. In particular, if C is a cone, so is its opposite cone -C.
Spherical section and projection
Let |·| be any normNorm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
for V, with the property that the norm of any vector is a scalar of V. Let S be the unit-norm sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
of V, that is, the set

By definition, a nonzero vector x belongs to a cone C of V if and only if the unit-norm vector x/|x| belongs to C. Therefore, a blunt (or pointed) cone C is completely specified by its central projection onto S; that is, by the set
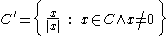
It follows that there is a one-to-one correspondence
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between blunt (or pointed) cones and subsets of S.
Indeed, the central projection C' is simply the spherical section of C, the set C
 S of its unit-norm elements.
S of its unit-norm elements.A cone C is closed with respect to the norm |·| if it is a closed set in the topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
induced by that norm. That is the case if and only if C is pointed and its spherical section is a closed subset of S.
Note that the cone C is salient if and only if its spherical section does not contain two opposite vectors; that is, C'
 (-C' ) = {}.
(-C' ) = {}.See also
- Cone (disambiguation)
- Cone (geometry)Cone (geometry)A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
- Cone (topology)Cone (topology)In topology, especially algebraic topology, the cone CX of a topological space X is the quotient space:CX = /\,of the product of X with the unit interval I = [0, 1]....
- Convex coneConvex coneIn linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:...
- Cone (geometry)
- Ordered groupOrdered groupIn abstract algebra, a partially-ordered group is a group equipped with a partial order "≤" that is translation-invariant; in other words, "≤" has the property that, for all a, b, and g in G, if a ≤ b then a+g ≤ b+g and g+a ≤ g+b.An element x of G is called positive element if 0 ≤ x...
with the concept of the "positive cone" - Ordered vector spaceOrdered vector spaceIn mathematics an ordered vector space or partially ordered vector space is a vector space equipped with a partial order which is compatible with the vector space operations.- Definition:...

