Transcendental number
Encyclopedia
In mathematics
, a transcendental number is a number (possibly a complex number
) that is not algebraic
—that is, it is not a root of a non-constant polynomial
equation with rational
coefficient
s. The most prominent examples of transcendental numbers are π
and e
. Though only a few classes of transcendental numbers are known (in part, because it can be extremely difficult to show that a given number is transcendental), transcendental numbers are not rare. Indeed, almost all
real
and complex numbers are transcendental, since the algebraic numbers are countable while the sets of real and complex numbers are uncountable. All real transcendental numbers are irrational
, since all rational numbers are algebraic. The converse is not true: not all irrational numbers are transcendental, e.g. the square root of 2
is irrational but is an algebraic number (therefore, not transcendental).
in his 1682 paper where he proved sin x is not an algebraic function
of x. Euler
was probably the first person to define transcendental numbers in the modern sense.
Joseph Liouville
first proved the existence of transcendental numbers in 1844, and in 1851 gave the first decimal examples such as the Liouville constant
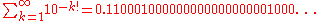
in which the nth digit after the decimal point is 1 if n is equal to k factorial (i.e., 1, 2, 6, 24, 120, 720, ...., etc.) and 0 otherwise. Liouville showed that this number is what we now call a Liouville number; this essentially means that it can be more closely approximated by rational number
s than can any algebraic number. Liouville showed that all Liouville numbers are transcendental.
Johann Heinrich Lambert
conjectured that e
and π
were both transcendental numbers in his 1761 paper proving the number π is irrational
. The first number to be proven transcendental without having been specifically constructed for the purpose was e, by Charles Hermite
in 1873.
In 1874, Georg Cantor
proved that the algebraic numbers are countable and the real numbers are uncountable. He also gave a new method
for constructing transcendental numbers. In 1878, Cantor published a construction that proves there are as many transcendental numbers as there are real numbers. Cantor's work established the ubiquity of transcendental numbers.
In 1882, Ferdinand von Lindemann
published a proof that the number π is transcendental. He first showed that e to any nonzero algebraic power is transcendental, and since eiπ = −1 is algebraic (see Euler's identity), iπ and therefore π must be transcendental. This approach was generalized by Karl Weierstrass
to the Lindemann–Weierstrass theorem
. The transcendence of π allowed the proof of the impossibility of several ancient geometric constructions involving compass and straightedge
, including the most famous one, squaring the circle
.
In 1900, David Hilbert
posed an influential question about transcendental numbers, Hilbert's seventh problem
: If a is an algebraic number, that is not zero or one, and b is an irrational algebraic number
, is ab necessarily transcendental? The affirmative answer was provided in 1934 by the Gelfond–Schneider theorem
. This work was extended by Alan Baker in the 1960s in his work on lower bounds for linear forms in any number of logarithms (of algebraic numbers).
s must also be countable. But Cantor's diagonal argument
proves that the real numbers (and therefore also the complex numbers) are uncountable; so the set of all transcendental numbers must also be uncountable.
No rational number
is transcendental and all real transcendental numbers are irrational.
A rational number can be written as p / q, where p and q are integers. Thus, p / q is the root of qx − p = 0.
However, some irrational number
s are not transcendental. For example, the square root of 2
is irrational and not transcendental (because it is a solution of the polynomial equation x2 − 2 = 0).
Any non-constant algebraic function
of a single variable yields a transcendental value when applied to a transcendental argument. For example, from knowing that π is transcendental, we can immediately deduce that numbers such as 5π, (π − 3)/√2, (√π − √3)8 and (π5 + 7)1/7 are transcendental as well.
However, an algebraic function of several variables may yield an algebraic number when applied to transcendental numbers if these numbers are not algebraically independent. For example, π and 1 − π are both transcendental, but π + (1 − π) = 1 is obviously not. It is unknown whether π + e, for example, is transcendental, though at least one of π + e and πe must be transcendental. More generally, for any two transcendental numbers a and b, at least one of a + b and ab must be transcendental. To see this, consider the polynomial (x − a) (x − b) = x2 − (a + b)x + ab. If (a + b) and ab were both algebraic, then this would be a polynomial with algebraic coefficients. Because algebraic numbers form an algebraically closed field
, this would imply that the roots of the polynomial, a and b, must be algebraic. But this is a contradiction, and thus it must be the case that at least one of the coefficients is transcendental.
The non-computable numbers
are a strict subset of the transcendental numbers.
All Liouville numbers are transcendental, but not vice versa. Any Liouville number must have unbounded partial quotients in its continued fraction
expansion. Using a counting argument one can show that there exist transcendental numbers which have bounded partial quotients and hence are not Liouville numbers.
Using the explicit continued fraction expansion of e, one can show that e is not a Liouville number (although the partial quotients in its continued fraction expansion are unbounded). Kurt Mahler
showed in 1953 that π is also not a Liouville number. It is conjectured that all infinite continued fractions with bounded terms that are not eventually periodic are transcendental (eventually periodic continued fractions correspond to quadratic irrationals).
A related class of numbers are closed-form numbers, which may be defined in various ways, including rational numbers (and in some definitions all algebraic numbers), but also allow exponentiation and logarithm.
Conjectures:
, is transcendental dates from 1873. We will now follow the strategy of David Hilbert
(1862–1943) who gave a simplification of the original proof of Charles Hermite
. The idea is the following:
Assume, for purpose of finding a contradiction, that e is algebraic. Then there exists a finite set of integer coefficients
satisfying the equation:
and such that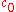
and 
are both non-zero.
Depending on the value of n, we specify a sufficiently large positive integer k (to meet our needs later), and multiply both sides of the above equation by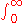
, where the notation 
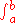will be used in this proof as shorthand for the integral:
We have arrived at the equation:
which can now be written in the form
where
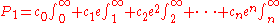
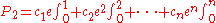
The plan now is to show that for k sufficiently large, the above relations are impossible to satisfy because
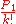is a non-zero integer and 
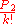is not.
The fact that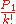
is a nonzero integer results from the relation
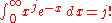
which is valid for any positive integer j by the definition of the Gamma function
.
It is non-zero because for every a satisfying
, the integrand in 
is 
times a sum of terms whose lowest power of x is k+1 after substituting x for 
in the integral. Then this becomes a sum of integrals of the form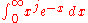 
with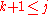 
, and (again, from the definition of the Gamma function) it is therefore a product of 
. Thus, after division by 
, we get zero modulo
(k+1) (i.e. a product of (k+1)). However, the integrand in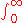
has a term of the form 
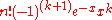and thus 
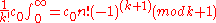. By choosing 
which is prime and larger than n and 
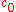, we get that 
is non-zero modulo (k+1) and is thus non-zero.
To show that
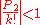for sufficiently large k
we construct an auxiliary function
, noting that it is the product of the functions 
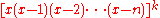and 
.
Using upper bounds for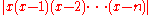
and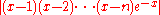 
on the interval
[0,n] and employing the fact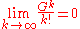
for every real number G
is then sufficient to finish the proof.
A similar strategy, different from Lindemann's original approach, can be used to show that the number π
is transcendental. Besides the gamma-function and some estimates as in the proof for e, facts about symmetric polynomial
s play a vital role in the proof.
For detailed information concerning the proofs of the transcendence of π and e see the references and external links.
in 1932 partitioned the transcendental numbers into 3 classes, called S, T, and U. Definition of these classes draws on an extension of the idea of a Liouville number (cited above).
Let m(x, 1, H) be the minimum non-zero absolute value these polynomials take.
Let ω(x, 1, H) = −log m(x, 1, H)/log H.
Let ω(x, 1) =
ω'(x, 1) is often called the measure of irrationality of a real number x. ω(x, 1) is 0 for rational numbers and is at least 1 for irrational real numbers. A Liouville number is defined to have infinite measure of irrationality.
Let m(x,n,H) be the minimum non-zero absolute value such polynomials take at x.
Let ω(x,n,H) = −log m(x,n,H)/n log H.
Let ω(x,n)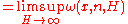
. Suppose this is infinite for some minimum positive integer n. A complex number x in this case is called a U number of degree n.
Now we can define ω(x)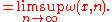
ω(x) is often called the measure of transcendence of x. If the ω(x,n) are bounded, then ω(x) is finite, and x is called an S number. If the ω(x,n) are finite but unbounded, x is called a T number. x is algebraic if and only if ω(x) = 0.
Clearly the Liouville numbers are a subset of the U numbers. William LeVeque in 1953 constructed U numbers of any desired degree. The Liouville numbers and hence the U numbers are uncountable sets. They are sets of measure 0.
T numbers also comprise a set of measure 0. It took about 35 years to show their existence. Wolfgang M. Schmidt
in 1968 showed that examples exist. It follows that almost all
complex numbers are S numbers. It has been shown that the exponential function sends all non-zero algebraic numbers to S numbers. Hence e is an S number. The most that is known about π is that it is not a U number. Many other transcendental numbers remain unclassified.
Two numbers x, y are called algebraically dependent if there is a non-zero polynomial P in 2 indeterminates with integer coefficients such that P(x, y) = 0. There is a powerful theorem that 2 complex numbers that are algebraically dependent belong to the same Mahler class. This allows construction of new transcendental numbers, such as the sum of a Liouville number with e or .
It is often speculated that S stood for the name of Mahler's teacher Carl Ludwig Siegel
and that T and U are just the next two letters.
Consider the approximation of a complex number x by algebraic numbers of degree ≤ n and height ≤ H. Let α be an algebraic number of this finite set such that |x - α| has the minimum positive value. Define ω*(x,H,n) by |x - α| = H-nω*(x,H,n) - 1. Let ω*(x,n)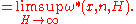
If for a smallest positive integer n, ω*(x,n) is infinite, x is called a U*-number of degree n.
If the ω*(x,n) are bounded and do not converge to 0, x is called an S*-number,
A number x is called an A*-number if the ω*(x,n) converge to 0.
If the ω*(x,n) are all finite but unbounded, x is called a T*-number,
Koksma's and Mahler's classifications are equivalent in that they divide the transcendental numbers into the same classes. The A*-numbers are the algebraic numbers.
of the sequence {ω(x, n)} is called the type. Almost all real numbers are S numbers of type 1, which is minimal for real S numbers. Almost all complex numbers are S numbers of type 1/2, which is also minimal. The claims of almost all numbers were conjectured by Mahler and in 1965 proved by Vladimir Sprindzhuk.
is transcendental (PDF)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a transcendental number is a number (possibly a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
) that is not algebraic
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
—that is, it is not a root of a non-constant polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
equation with rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s. The most prominent examples of transcendental numbers are π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
and e
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
. Though only a few classes of transcendental numbers are known (in part, because it can be extremely difficult to show that a given number is transcendental), transcendental numbers are not rare. Indeed, almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
and complex numbers are transcendental, since the algebraic numbers are countable while the sets of real and complex numbers are uncountable. All real transcendental numbers are irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
, since all rational numbers are algebraic. The converse is not true: not all irrational numbers are transcendental, e.g. the square root of 2
Square root of 2
The square root of 2, often known as root 2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.Geometrically the square root of 2 is the...
is irrational but is an algebraic number (therefore, not transcendental).
History
The name "transcendental" comes from LeibnizGottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
in his 1682 paper where he proved sin x is not an algebraic function
Algebraic function
In mathematics, an algebraic function is informally a function that satisfies a polynomial equation whose coefficients are themselves polynomials with rational coefficients. For example, an algebraic function in one variable x is a solution y for an equationwhere the coefficients ai are polynomial...
of x. Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
was probably the first person to define transcendental numbers in the modern sense.
Joseph Liouville
Joseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
first proved the existence of transcendental numbers in 1844, and in 1851 gave the first decimal examples such as the Liouville constant
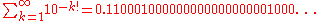
in which the nth digit after the decimal point is 1 if n is equal to k factorial (i.e., 1, 2, 6, 24, 120, 720, ...., etc.) and 0 otherwise. Liouville showed that this number is what we now call a Liouville number; this essentially means that it can be more closely approximated by rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s than can any algebraic number. Liouville showed that all Liouville numbers are transcendental.
Johann Heinrich Lambert
Johann Heinrich Lambert
Johann Heinrich Lambert was a Swiss mathematician, physicist, philosopher and astronomer.Asteroid 187 Lamberta was named in his honour.-Biography:...
conjectured that e
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
and π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
were both transcendental numbers in his 1761 paper proving the number π is irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
. The first number to be proven transcendental without having been specifically constructed for the purpose was e, by Charles Hermite
Charles Hermite
Charles Hermite was a French mathematician who did research on number theory, quadratic forms, invariant theory, orthogonal polynomials, elliptic functions, and algebra....
in 1873.
In 1874, Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
proved that the algebraic numbers are countable and the real numbers are uncountable. He also gave a new method
Cantor's first uncountability proof
Georg Cantor's first uncountability proof demonstrates that the set of all real numbers is uncountable. This proof differs from the more familiar proof that uses his diagonal argument...
for constructing transcendental numbers. In 1878, Cantor published a construction that proves there are as many transcendental numbers as there are real numbers. Cantor's work established the ubiquity of transcendental numbers.
In 1882, Ferdinand von Lindemann
Ferdinand von Lindemann
Carl Louis Ferdinand von Lindemann was a German mathematician, noted for his proof, published in 1882, that π is a transcendental number, i.e., it is not a root of any polynomial with rational coefficients....
published a proof that the number π is transcendental. He first showed that e to any nonzero algebraic power is transcendental, and since eiπ = −1 is algebraic (see Euler's identity), iπ and therefore π must be transcendental. This approach was generalized by Karl Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
to the Lindemann–Weierstrass theorem
Lindemann–Weierstrass theorem
In mathematics, the Lindemann–Weierstrass theorem is a result that is very useful in establishing the transcendence of numbers. It states that if 1, ..., are algebraic numbers which are linearly independent over the rational numbers ', then 1, ..., are algebraically...
. The transcendence of π allowed the proof of the impossibility of several ancient geometric constructions involving compass and straightedge
Compass and straightedge
Compass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass....
, including the most famous one, squaring the circle
Squaring the circle
Squaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedge...
.
In 1900, David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
posed an influential question about transcendental numbers, Hilbert's seventh problem
Hilbert's seventh problem
Hilbert's seventh problem is one of David Hilbert's list of open mathematical problems posed in 1900. It concerns the irrationality and transcendence of certain numbers...
: If a is an algebraic number, that is not zero or one, and b is an irrational algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
, is ab necessarily transcendental? The affirmative answer was provided in 1934 by the Gelfond–Schneider theorem
Gelfond–Schneider theorem
In mathematics, the Gelfond–Schneider theorem establishes the transcendence of a large class of numbers. It was originally proved independently in 1934 by Aleksandr Gelfond and Theodor Schneider...
. This work was extended by Alan Baker in the 1960s in his work on lower bounds for linear forms in any number of logarithms (of algebraic numbers).
Properties
The set of transcendental numbers is uncountably infinite. Since the polynomials with integer coefficients are countable, and since each such polynomial has a finite number of zeroes, the algebraic numberAlgebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s must also be countable. But Cantor's diagonal argument
Cantor's diagonal argument
Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural...
proves that the real numbers (and therefore also the complex numbers) are uncountable; so the set of all transcendental numbers must also be uncountable.
No rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
is transcendental and all real transcendental numbers are irrational.
A rational number can be written as p / q, where p and q are integers. Thus, p / q is the root of qx − p = 0.
However, some irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s are not transcendental. For example, the square root of 2
Square root of 2
The square root of 2, often known as root 2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.Geometrically the square root of 2 is the...
is irrational and not transcendental (because it is a solution of the polynomial equation x2 − 2 = 0).
Any non-constant algebraic function
Algebraic function
In mathematics, an algebraic function is informally a function that satisfies a polynomial equation whose coefficients are themselves polynomials with rational coefficients. For example, an algebraic function in one variable x is a solution y for an equationwhere the coefficients ai are polynomial...
of a single variable yields a transcendental value when applied to a transcendental argument. For example, from knowing that π is transcendental, we can immediately deduce that numbers such as 5π, (π − 3)/√2, (√π − √3)8 and (π5 + 7)1/7 are transcendental as well.
However, an algebraic function of several variables may yield an algebraic number when applied to transcendental numbers if these numbers are not algebraically independent. For example, π and 1 − π are both transcendental, but π + (1 − π) = 1 is obviously not. It is unknown whether π + e, for example, is transcendental, though at least one of π + e and πe must be transcendental. More generally, for any two transcendental numbers a and b, at least one of a + b and ab must be transcendental. To see this, consider the polynomial (x − a) (x − b) = x2 − (a + b)x + ab. If (a + b) and ab were both algebraic, then this would be a polynomial with algebraic coefficients. Because algebraic numbers form an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
, this would imply that the roots of the polynomial, a and b, must be algebraic. But this is a contradiction, and thus it must be the case that at least one of the coefficients is transcendental.
The non-computable numbers
Computable number
In mathematics, particularly theoretical computer science and mathematical logic, the computable numbers, also known as the recursive numbers or the computable reals, are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm...
are a strict subset of the transcendental numbers.
All Liouville numbers are transcendental, but not vice versa. Any Liouville number must have unbounded partial quotients in its continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
expansion. Using a counting argument one can show that there exist transcendental numbers which have bounded partial quotients and hence are not Liouville numbers.
Using the explicit continued fraction expansion of e, one can show that e is not a Liouville number (although the partial quotients in its continued fraction expansion are unbounded). Kurt Mahler
Kurt Mahler
Kurt Mahler was a mathematician and Fellow of the Royal Society.He was a student at the universities in Frankfurt and Göttingen, graduating with a Ph.D...
showed in 1953 that π is also not a Liouville number. It is conjectured that all infinite continued fractions with bounded terms that are not eventually periodic are transcendental (eventually periodic continued fractions correspond to quadratic irrationals).
A related class of numbers are closed-form numbers, which may be defined in various ways, including rational numbers (and in some definitions all algebraic numbers), but also allow exponentiation and logarithm.
Numbers proven to be transcendental
Numbers proven to be transcendental:- eE (mathematical constant)The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
a if a is algebraic and nonzero (by the Lindemann–Weierstrass theoremLindemann–Weierstrass theoremIn mathematics, the Lindemann–Weierstrass theorem is a result that is very useful in establishing the transcendence of numbers. It states that if 1, ..., are algebraic numbers which are linearly independent over the rational numbers ', then 1, ..., are algebraically...
), and in particular, e itself. - πPi' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
(by the Lindemann–Weierstrass theoremLindemann–Weierstrass theoremIn mathematics, the Lindemann–Weierstrass theorem is a result that is very useful in establishing the transcendence of numbers. It states that if 1, ..., are algebraic numbers which are linearly independent over the rational numbers ', then 1, ..., are algebraically...
). - eπ, Gelfond's constantGelfond's constantIn mathematics, Gelfond's constant, named after Aleksandr Gelfond, is eπ, that is, e to the power of π. Like both e and π, this constant is a transcendental number. This can be proven by the Gelfond–Schneider theorem and noting the fact that...
, as well as e-π/2=i i (by the Gelfond–Schneider theoremGelfond–Schneider theoremIn mathematics, the Gelfond–Schneider theorem establishes the transcendence of a large class of numbers. It was originally proved independently in 1934 by Aleksandr Gelfond and Theodor Schneider...
). - ab where a is algebraic but not 0 or 1, and b is irrational algebraic (by the Gelfond–Schneider theorem), in particular:
-
, the Gelfond–Schneider constant (Hilbert number).
-
- sinTrigonometric functionIn mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
(a), cos(a) and tan(a), and their multiplicative inverses csc(a), sec(a) and cot(a), for any nonzero algebraic number a (by the Lindemann–Weierstrass theorem). - lnNatural logarithmThe natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
(a) if a is algebraic and not equal to 0 or 1, for any branch of the logarithm function (by the Lindemann–Weierstrass theorem). - W(a) if a is algebraic and nonzero, for any branch of the Lambert W Function (by the Lindemann–Weierstrass theorem).
- ΓGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
(1/3), Γ(1/4), and Γ(1/6). - 0.12345678910111213141516..., the Champernowne constantChampernowne constantIn mathematics, the Champernowne constant C10 is a transcendental real constant whose decimal expansion has important properties. It is named after mathematician D. G...
. - Ω, Chaitin's constantChaitin's constantIn the computer science subfield of algorithmic information theory, a Chaitin constant or halting probability is a real number that informally represents the probability that a randomly constructed program will halt...
(since it is a non-computable number). - Prouhet–Thue–Morse constant
-
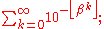where 
and 
is the floor functionFloor functionIn mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
.
Numbers which may or may not be transcendental
Numbers which have neither been proven algebraic nor proven transcendental:- Sums, products, powers, etc. of the number π and the number eE (mathematical constant)The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
, except for eπ, Gelfond's constantGelfond's constantIn mathematics, Gelfond's constant, named after Aleksandr Gelfond, is eπ, that is, e to the power of π. Like both e and π, this constant is a transcendental number. This can be proven by the Gelfond–Schneider theorem and noting the fact that...
, which is known to be transcendental: π + e, π − e, π·e, π/e, ππ, ee, πe. - The Euler–Mascheroni constantEuler–Mascheroni constantThe Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
γ (which has not even been proven to be irrational). - Catalan's constant, also not known to be irrational.
- Apéry's constantApéry's constantIn mathematics, Apéry's constant is a number that occurs in a variety of situations. It arises naturally in a number of physical problems, including in the second- and third-order terms of the electron's gyromagnetic ratio using quantum electrodynamics...
, ζ(3), and in fact, ζ(2n + 1) for any positive integer n (see Riemann zeta function). - The Feigenbaum constantsFeigenbaum constantsThe Feigenbaum constants are two mathematical constants named after the mathematician Mitchell Feigenbaum. Both express ratios in a bifurcation diagram.The first Feigenbaum constant ,...
,
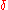and 
.
Conjectures:
- Schanuel's conjectureSchanuel's conjectureIn mathematics, specifically transcendence theory, Schanuel's conjecture is a conjecture made by Stephen Schanuel in the 1960s concerning the transcendence degree of certain field extensions of the rational numbers.-Statement:The conjecture is as follows:...
, - Four exponentials conjectureFour exponentials conjectureIn mathematics, specifically the field of transcendental number theory, the four exponentials conjecture is a conjecture which, given the right conditions on the exponents, would guarantee the transcendence of at least one of four exponentials...
.
Sketch of a proof that e is transcendental
The first proof that the base of the natural logarithms, eE (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
, is transcendental dates from 1873. We will now follow the strategy of David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
(1862–1943) who gave a simplification of the original proof of Charles Hermite
Charles Hermite
Charles Hermite was a French mathematician who did research on number theory, quadratic forms, invariant theory, orthogonal polynomials, elliptic functions, and algebra....
. The idea is the following:
Assume, for purpose of finding a contradiction, that e is algebraic. Then there exists a finite set of integer coefficients
satisfying the equation:and such that
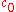and are both non-zero.Depending on the value of n, we specify a sufficiently large positive integer k (to meet our needs later), and multiply both sides of the above equation by
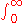, where the notation 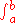will be used in this proof as shorthand for the integral:We have arrived at the equation:
which can now be written in the form
where
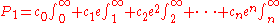
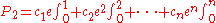
The plan now is to show that for k sufficiently large, the above relations are impossible to satisfy because
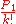is a non-zero integer and 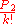is not.The fact that
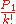is a nonzero integer results from the relation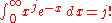which is valid for any positive integer j by the definition of the Gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
.
It is non-zero because for every a satisfying
, the integrand in is times a sum of terms whose lowest power of x is k+1 after substituting x for in the integral. Then this becomes a sum of integrals of the form 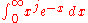with 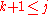, and (again, from the definition of the Gamma function) it is therefore a product of . Thus, after division by , we get zero moduloModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
(k+1) (i.e. a product of (k+1)). However, the integrand in
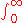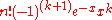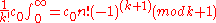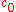has a term of the form and thus . By choosing which is prime and larger than n and , we get that is non-zero modulo (k+1) and is thus non-zero.To show that
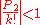for sufficiently large kwe construct an auxiliary function
Auxiliary function
In mathematics, auxiliary functions are an important construction in transcendental number theory. They are functions that appear in most proofs in this area of mathematics and that have specific, desirable properties, such as taking the value zero for many arguments, or having a zero of high...
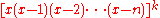, noting that it is the product of the functions and .Using upper bounds for
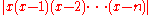and 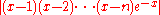on the intervalInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[0,n] and employing the fact
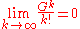for every real number Gis then sufficient to finish the proof.
A similar strategy, different from Lindemann's original approach, can be used to show that the number π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
is transcendental. Besides the gamma-function and some estimates as in the proof for e, facts about symmetric polynomial
Symmetric polynomial
In mathematics, a symmetric polynomial is a polynomial P in n variables, such that if any of the variables are interchanged, one obtains the same polynomial...
s play a vital role in the proof.
For detailed information concerning the proofs of the transcendence of π and e see the references and external links.
Mahler's classification
Kurt MahlerKurt Mahler
Kurt Mahler was a mathematician and Fellow of the Royal Society.He was a student at the universities in Frankfurt and Göttingen, graduating with a Ph.D...
in 1932 partitioned the transcendental numbers into 3 classes, called S, T, and U. Definition of these classes draws on an extension of the idea of a Liouville number (cited above).
Measure of irrationality of a real number
One way to define a Liouville number is to consider how small a given real number x makes linear polynomials |qx − p| without making them exactly 0. Here p, q are integers with |p|, |q| bounded by a positive integer H.Let m(x, 1, H) be the minimum non-zero absolute value these polynomials take.
Let ω(x, 1, H) = −log m(x, 1, H)/log H.
Let ω(x, 1) =
ω'(x, 1) is often called the measure of irrationality of a real number x. ω(x, 1) is 0 for rational numbers and is at least 1 for irrational real numbers. A Liouville number is defined to have infinite measure of irrationality.
Measure of transcendence of a complex number
Next consider the values of polynomials at a complex number x, when these polynomials have integer coefficients, degree at most n, and height at most H, with n, H being positive integers.Let m(x,n,H) be the minimum non-zero absolute value such polynomials take at x.
Let ω(x,n,H) = −log m(x,n,H)/n log H.
Let ω(x,n)
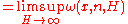. Suppose this is infinite for some minimum positive integer n. A complex number x in this case is called a U number of degree n.Now we can define ω(x)
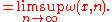ω(x) is often called the measure of transcendence of x. If the ω(x,n) are bounded, then ω(x) is finite, and x is called an S number. If the ω(x,n) are finite but unbounded, x is called a T number. x is algebraic if and only if ω(x) = 0.Clearly the Liouville numbers are a subset of the U numbers. William LeVeque in 1953 constructed U numbers of any desired degree. The Liouville numbers and hence the U numbers are uncountable sets. They are sets of measure 0.
T numbers also comprise a set of measure 0. It took about 35 years to show their existence. Wolfgang M. Schmidt
Wolfgang M. Schmidt
Wolfgang M. Schmidt is a mathematician born in 1933. He studied mathematics at the University of Vienna, where he received his PhD, which was supervised by Edmund Hlawka, in 1955...
in 1968 showed that examples exist. It follows that almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
complex numbers are S numbers. It has been shown that the exponential function sends all non-zero algebraic numbers to S numbers. Hence e is an S number. The most that is known about π is that it is not a U number. Many other transcendental numbers remain unclassified.
Two numbers x, y are called algebraically dependent if there is a non-zero polynomial P in 2 indeterminates with integer coefficients such that P(x, y) = 0. There is a powerful theorem that 2 complex numbers that are algebraically dependent belong to the same Mahler class. This allows construction of new transcendental numbers, such as the sum of a Liouville number with e or .
It is often speculated that S stood for the name of Mahler's teacher Carl Ludwig Siegel
Carl Ludwig Siegel
Carl Ludwig Siegel was a mathematician specialising in number theory and celestial mechanics. He was one of the most important mathematicians of the 20th century.-Biography:...
and that T and U are just the next two letters.
Koksma's equivalent classification
Jurjen Koksma in 1939 proposed another classification based on approximation by algebraic numbers.Consider the approximation of a complex number x by algebraic numbers of degree ≤ n and height ≤ H. Let α be an algebraic number of this finite set such that |x - α| has the minimum positive value. Define ω*(x,H,n) by |x - α| = H-nω*(x,H,n) - 1. Let ω*(x,n)
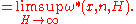
If for a smallest positive integer n, ω*(x,n) is infinite, x is called a U*-number of degree n.
If the ω*(x,n) are bounded and do not converge to 0, x is called an S*-number,
A number x is called an A*-number if the ω*(x,n) converge to 0.
If the ω*(x,n) are all finite but unbounded, x is called a T*-number,
Koksma's and Mahler's classifications are equivalent in that they divide the transcendental numbers into the same classes. The A*-numbers are the algebraic numbers.
Type
The supremumSupremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of the sequence {ω(x, n)} is called the type. Almost all real numbers are S numbers of type 1, which is minimal for real S numbers. Almost all complex numbers are S numbers of type 1/2, which is also minimal. The claims of almost all numbers were conjectured by Mahler and in 1965 proved by Vladimir Sprindzhuk.
External links
Proof that e is transcendental Proof that the Liouville Constant is transcendental Proof that e is transcendental (PDF) Proof that is transcendental (PDF)