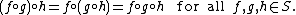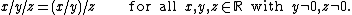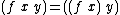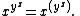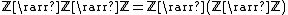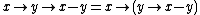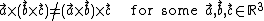
Associativity
Encyclopedia
In mathematics
, associativity is a property of some binary operation
s. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operand
s is not changed. That is, rearranging the parentheses in such an expression will not change its value. Consider, for instance, the following equations:
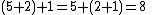
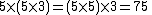
Consider the first equation. Even though the parentheses were rearranged (the left side requires adding 5 and 2 first, then adding 1 to the result, whereas the right side requires adding 2 and 1 first, then 5), the value of the expression was not altered. Since this holds true when performing addition on any real number
s, we say that "addition of real numbers is an associative operation."
Associativity is not to be confused with commutativity
. Commutativity justifies changing the order or sequence of the operands within an expression while associativity does not. For example,
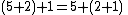
is an example of associativity because the parentheses were changed (and consequently the order of operations during evaluation) while the operands 5, 2, and 1 appeared in exactly the same order from left to right in the expression. In contrast,
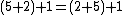
is an example of commutativity, not associativity, because the operand sequence changed when the 2 and 5 switched places.
Associative operations are abundant in mathematics; in fact, many algebraic structure
s (such as semigroups and categories
) explicitly require their binary operations to be associative.
However, many important and interesting operations are non-associative; one common example would be the vector cross product.
on a set S is called associative if it satisfies the associative law:
The evaluation order does not affect the value of such expressions, and it can be shown that the same holds for expressions containing any number of
operations. Thus, when 
is associative, the evaluation order can therefore be left unspecified without causing ambiguity, by omitting the parentheses and writing simply:
However, it is important to remember that changing the order of operations does not involve or permit moving the operands around within the expression; the sequence of operands is always unchanged.
A different perspective is obtained by rephrasing associativity using functional notation: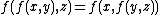
: when expressed in this form, associativity becomes less obvious.
Associativity can be generalized to n-ary operations
. Ternary associativity is (abc)de = a(bcd)e = ab(cde), i.e. the string abcde with any three adjacent elements bracketed. N-ary associativity is a string of length n+(n-1) with any n adjacent elements bracketed.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, associativity is a property of some binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operand
Operand
In mathematics, an operand is the object of a mathematical operation, a quantity on which an operation is performed.-Example :The following arithmetic expression shows an example of operators and operands:3 + 6 = 9\;...
s is not changed. That is, rearranging the parentheses in such an expression will not change its value. Consider, for instance, the following equations:
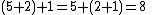
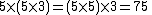
Consider the first equation. Even though the parentheses were rearranged (the left side requires adding 5 and 2 first, then adding 1 to the result, whereas the right side requires adding 2 and 1 first, then 5), the value of the expression was not altered. Since this holds true when performing addition on any real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, we say that "addition of real numbers is an associative operation."
Associativity is not to be confused with commutativity
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
. Commutativity justifies changing the order or sequence of the operands within an expression while associativity does not. For example,
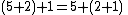
is an example of associativity because the parentheses were changed (and consequently the order of operations during evaluation) while the operands 5, 2, and 1 appeared in exactly the same order from left to right in the expression. In contrast,
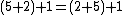
is an example of commutativity, not associativity, because the operand sequence changed when the 2 and 5 switched places.
Associative operations are abundant in mathematics; in fact, many algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s (such as semigroups and categories
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
) explicitly require their binary operations to be associative.
However, many important and interesting operations are non-associative; one common example would be the vector cross product.
Definition
Formally, a binary operation on a set S is called associative if it satisfies the associative law:-
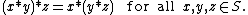
- Using * to denote a binary operationBinary operationIn mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
performed on a set
-
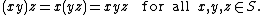
- An example of multiplicative associativity
The evaluation order does not affect the value of such expressions, and it can be shown that the same holds for expressions containing any number of
operations. Thus, when is associative, the evaluation order can therefore be left unspecified without causing ambiguity, by omitting the parentheses and writing simply:However, it is important to remember that changing the order of operations does not involve or permit moving the operands around within the expression; the sequence of operands is always unchanged.
A different perspective is obtained by rephrasing associativity using functional notation:
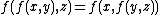: when expressed in this form, associativity becomes less obvious.Associativity can be generalized to n-ary operations
Arity
In logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
. Ternary associativity is (abc)de = a(bcd)e = ab(cde), i.e. the string abcde with any three adjacent elements bracketed. N-ary associativity is a string of length n+(n-1) with any n adjacent elements bracketed.
Examples
Some examples of associative operations include the following.- The prototypical example of an associative operation is string concatenation: the concatenation of
"hello",", ","world"can be computed by concatenating the first two strings (giving"hello, ") and appending the third string ("world"), or by joining the second and third string (giving", world") and concatenating the first string ("hello") with the result. String concatenation is not commutative.
- In arithmeticArithmeticArithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
, additionAdditionAddition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and multiplicationMultiplicationMultiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
of real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s are associative; i.e.,
-
-
- Addition and multiplication of complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s and quaternionQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s is associative. Addition of octonionOctonionIn mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s is also associative, but multiplication of octonions is non-associative.
- The greatest common divisorGreatest common divisorIn mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
and least common multipleLeast common multipleIn arithmetic and number theory, the least common multiple of two integers a and b, usually denoted by LCM, is the smallest positive integer that is a multiple of both a and b...
functions act associatively.
-
-
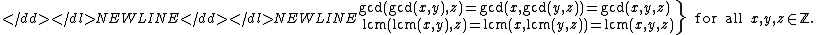
- Because linear transformationLinear transformationIn mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s are functions that can be represented by matrices with matrix multiplicationMatrix multiplicationIn mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
being the representation of functional composition, one can immediately conclude that matrix multiplication is associative.
- Taking the intersectionIntersection (set theory)In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
or the unionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of sets:
-
-
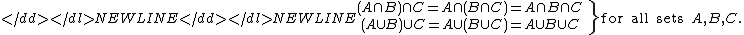
- If M is some set and S denotes the set of all functions from M to M, then the operation of functional composition on S is associative:
- Slightly more generally, given four sets M, N, P and Q, with h: M to N, g: N to P, and f: P to Q, then
- as before. In short, composition of maps is always associative.
- Consider a set with three elements, A, B, and C. The following operation:
+ × A B C A A A A B A B C C A A A
is associative. Thus, for example, A(BC)=(AB)C. This mapping is not commutative.
Non-associativity
A binary operation
on a set S that does not satisfy the associative law is called non-associative. Symbolically,
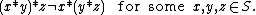
For such an operation the order of evaluation does matter. For example:
- SubtractionSubtractionIn arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
- DivisionDivision (mathematics)right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
- ExponentiationExponentiationExponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
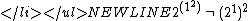
Also note that infinite sums are not generally associative, for example: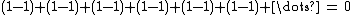
whereas
The study of non-associative structures arises from reasons somewhat different from the mainstream of classical algebra. One area within non-associative algebra that has grown very large is that of Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s. There the associative law is replaced by the Jacobi identityJacobi identityIn mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
. Lie algebras abstract the essential nature of infinitesimal transformationInfinitesimal transformationIn mathematics, an infinitesimal transformation is a limiting form of small transformation. For example one may talk about an infinitesimal rotation of a rigid body, in three-dimensional space. This is conventionally represented by a 3×3 skew-symmetric matrix A...
s, and have become ubiquitous in mathematics. They are an example of non-associative algebraNon-associative algebraA non-associative algebra over a field K is a K-vector space A equipped with a K-bilinear map A × A → A. There are left and right multiplication maps...
s.
There are other specific types of non-associative structures that have been studied in depth. They tend to come from some specific applications. Some of these arise in combinatorial mathematics. Other examples: QuasigroupQuasigroupIn mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...
, QuasifieldQuasifieldIn mathematics, a quasifield is an algebraic structure where + and \cdot are binary operations on Q, much like a division ring, but with some weaker conditions.-Definition:A quasifield is a structure, where + and...
, Nonassociative ringNonassociative ringIn abstract algebra, a nonassociative ring is a generalization of the concept of ring.A nonassociative ring is a set R with two operations, addition and multiplication, such that:# R is an abelian group under addition:## a+b = b+a...
.
Notation for non-associative operations
In general, parentheses must be used to indicate the order of evaluationOrder of operationsIn mathematics and computer programming, the order of operations is a rule used to clarify unambiguously which procedures should be performed first in a given mathematical expression....
if a non-associative operation appears more than once in an expression. However, mathematicianMathematicianA mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s agree on a particular order of evaluation for several common non-associative operations. This is simply a notational convention to avoid parentheses.
A left-associative operation is a non-associative operation that is conventionally evaluated from left to right, i.e.,
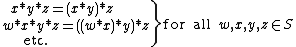
while a right-associative operation is conventionally evaluated from right to left:
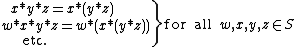
Both left-associative and right-associative operations occur. Left-associative operations include the following:
- Subtraction and division of real numbers:
- Function application:
-
- This notation can be motivated by the curryingCurryingIn mathematics and computer science, currying is the technique of transforming a function that takes multiple arguments in such a way that it can be called as a chain of functions each with a single argument...
isomorphism.
Right-associative operations include the following:
- ExponentiationExponentiationExponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
of real numbers:
- The reason exponentiation is right-associative is that a repeated left-associative exponentiation operation would be less useful. Multiple appearances could (and would) be rewritten with multiplication:
- Function definitionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
- Using right-associative notation for these operations can be motivated by the Curry-Howard correspondence and by the curryingCurryingIn mathematics and computer science, currying is the technique of transforming a function that takes multiple arguments in such a way that it can be called as a chain of functions each with a single argument...
isomorphism.
Non-associative operations for which no conventional evaluation order is defined include the following.
- Taking the Cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
of three vectors:
- Taking the pairwise averageAverageIn mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....
of real numbers:
-
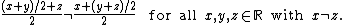
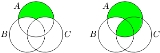
- Taking the relative complementComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of sets:
- Taking the relative complement
The green part in the left Venn diagramVenn diagramVenn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets . Venn diagrams were conceived around 1880 by John Venn...
represents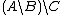
. The green part in the right Venn diagramVenn diagramVenn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets . Venn diagrams were conceived around 1880 by John Venn...
represents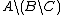
.
See also
- Light's associativity testLight's associativity testIn mathematics, Light's associativity test is a procedure invented by F W Light for testing whether a binary operation defined in a finite set by a Cayley multiplication table is associative. Direct verification of the associativity of a binary operation specified by a Cayley table is cumbersome...
- A semigroupSemigroupIn mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
is a set with a closed associative binary operation. - CommutativityCommutativityIn mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
and distributivityDistributivityIn mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
are two other frequently discussed properties of binary operations. - Power associativityPower associativityIn abstract algebra, power associativity is a property of a binary operation which is a weak form of associativity.An algebra is said to be power-associative if the subalgebra generated by any element is associative....
and alternativityAlternativityIn abstract algebra, alternativity is a property of a binary operation. A magma G is said to be left alternative if y = x for all x and y in G and right alternative if y = x for all x and y in G...
are weak forms of associativity.
- Exponentiation
- Division
-
- Because linear transformation
-
- Addition and multiplication of complex number
-
