
Representation theory
Encyclopedia
Representation theory is a branch of mathematics
that studies abstract
algebraic structure
s by representing their elements as linear transformation
s of vector space
s, and studies
modules
over these abstract algebraic structures. In essence, a representation makes an abstract algebraic object more concrete by describing its elements by matrices
and the algebraic operations in terms of matrix addition
and matrix multiplication
. The algebra
ic objects amenable to such a description include groups
, associative algebra
s and Lie algebra
s. The most prominent of these (and historically the first) is the representation theory of groups
, in which elements of a group are represented by invertible matrices in such a way that the group operation is matrix multiplication.
Representation theory is a powerful tool because it reduces problems in abstract algebra
to problems in linear algebra
, a subject which is well understood. Furthermore, the vector space on which a group (for example) is represented can be infinite dimensional, and by allowing it to be, for instance, a Hilbert space
, methods of analysis
can be applied to the theory of groups. Representation theory is also important in physics
because, for example, it describes how the symmetry group
of a physical system affects the solutions of equations describing that system.
A striking feature of representation theory is its pervasiveness in mathematics. There are two sides to this. First, the applications of representation theory are diverse: in addition to its impact on algebra, representation theory illuminates and vastly generalizes Fourier analysis via harmonic analysis
, is deeply connected to geometry
via invariant theory
and the Erlangen program
, and has a profound impact in number theory via automorphic form
s and the Langlands program
. The second aspect is the diversity of approaches to representation theory. The same objects can be studied using methods from algebraic geometry
, module theory, analytic number theory
, differential geometry, operator theory
and topology
.
The success of representation theory has led to numerous generalizations. One of the most general is a categorical one
. The algebraic objects to which representation theory applies can be viewed as particular kinds of categories, and the representations as functor
s from the object category to the category of vector spaces
. This description points to two obvious generalizations: first, the algebraic objects can be replaced by more general categories; second the target category of vector spaces can be replaced by other well-understood categories.
over a field
F. For instance, suppose V is Rn or Cn, the standard n-dimensional space of column vectors over the real
or complex number
s respectively. In this case, the idea of representation theory is to do abstract algebra
concretely by using n × n matrices
of real or complex numbers.
There are three main sorts of algebra
ic objects for which this can be done: groups
, associative algebra
s and Lie algebra
s.
This generalizes to any field F and any vector space V over F, with linear maps replacing matrices and composition
replacing matrix multiplication: there is a group GL(V,F) of automorphisms of V, an associative algebra EndF(V) of all endomorphisms of V, and a corresponding Lie algebra gl(V,F).
, generalizing the way that matrices act on column vectors by matrix multiplication. A representation of a group
G or (associative or Lie) algebra A on a vector space V is a map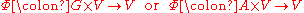
with two properties. First, for any g in G (or a in A), the map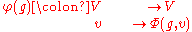
is linear (over F), and similarly in the algebra cases. Second, if we introduce the notation g · v for Φ (g, v), then for any g1, g2 in G and v in V: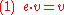
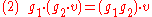
where e is the identity element
of G and g1g2 is product in G. The requirement for associative algebras is analogous, except that associative algebras do not always have an identity element, in which case equation (1) is ignored. Equation (2) is an abstract expression of the associativity of matrix multiplication. This doesn't hold for the matrix commutator and also there is no identity element for the commutator. Hence for Lie algebras, the only requirement is that for any x1, x2 in A and v in V:
where [x1, x2] is the Lie bracket
, which generalizes the matrix commutator MN − NM.
The second way to define a representation focuses on the map φ sending g in G to φ(g): V → V, which satisfies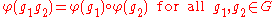
and similarly in the other cases. This approach is both more concise and more abstract.
When V is of finite dimension n, one can choose a basis
for V to identify V with Fn and hence recover a matrix representation with entries in the field F.
An effective or faithful representation
is a representation (V,φ) for which the homomorphism φ is injective.
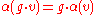
for all g in G and v in V. In terms of φ: G → GL(V) and ψ: G → GL(W), this means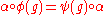
for all g in G.
Equivariant maps for representations of an associative or Lie algebra are defined similarly. If α is invertible, then it is said to be an isomorphism
, in which case V and W (or, more precisely, φ and ψ) are isomorphic representations.
Isomorphic representations are, for all practical purposes, "the same": they provide the same information about the group or algebra being represented. Representation theory therefore seeks to classify representations "up to isomorphism".
W/V can also be made into a representation of G.
If W has exactly two subrepresentations, namely the trivial subspace {0} and W itself, then the representation is said to be irreducible; if W has a proper nontrivial subrepresentation, the representation is said to be reducible.
The definition of an irreducible representation implies Schur's lemma
: an equivariant map α: V → W between irreducible representations is either the zero map or an isomorphism, since its kernel and image
are subrepresentations. In particular, when V = W, this shows that the equivariant endomorphism
s of V form an associative division algebra
over the underlying field F. If F is algebraically closed, the only equivariant endomorphisms of an irreducible representation are the scalar multiples of the identity.
Irreducible representations are the building blocks of representation theory: if a representation W is not irreducible then it is built from a subrepresentation and a quotient which are both "simpler" in some sense; for instance, if W is finite dimensional, then both the subrepresentation and the quotient have smaller dimension.
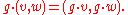
The direct sum of two representations carries no more information about the group G than the two representations do individually. If a representation is the direct sum of two proper nontrivial subrepresentations, it is said to be decomposable. Otherwise, it is said to be indecomposable.
In favourable circumstances, every representation is a direct sum of irreducible representations: such representations are said to be semisimple. In this case, it suffices to understand only the irreducible representations. In other cases, one must understand how indecomposable representations can be built from irreducible representations as extensions of a quotient by a subrepresentation.
Over a field of characteristic zero, the representation theory of a finite group G has a number of convenient properties. First, the representations of G are semisimple (completely reducible). This is a consequence of Maschke's theorem
, which states that any subrepresentation V of a G-representation W has a G-invariant complement. One proof is to choose any projection
π from W to V and replace it by its average
πG defined by
πG is equivariant, and its kernel is the required complement.
The finite dimensional G-representations can be understood using character theory
: the character of a representation φ: G → GL(V) is the class function χφ: G → F defined by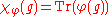
where is the trace. An irreducible representation of G is completely determined by its character.
is the trace. An irreducible representation of G is completely determined by its character.
Maschke's theorem holds more generally for fields of positive characteristic p, such as the finite field
s, as long as the prime p is coprime
to the order of G. When p and |G| have a common factor, there are G-representations which are not semisimple, which are studied in a subbranch called modular representation theory
.
Averaging techniques also show that if F is the real or complex numbers, then any G-representation preserves an inner product on V in the sense that
on V in the sense that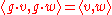
for all g in G and v, w in W. Hence any G-representation is unitary
.
Unitary representations are automatically semisimple, since Maschke's result can be proven by taking the orthogonal complement of a subrepresentation. When studying representations of groups which are not finite, the unitary representations provide a good generalization of the real and complex representations of a finite group.
Results such as Maschke's theorem and the unitary property which rely on averaging can be generalized to more general groups by replacing the average with an integral, provided that a suitable notion of integral can be defined. This can be done for compact group
s or locally compact group
s, using Haar measure
, and the resulting theory is known as abstract harmonic analysis.
Over arbitrary fields, another class of finite groups which have a good representation theory are the finite groups of Lie type. Important examples are linear algebraic group
s over finite fields. The representation theory of linear algebraic groups and Lie group
s extends these examples to infinite dimensional groups, the latter being intimately related to Lie algebra representations. The importance of character theory for finite groups has an analogue in the theory of weights
for representations of Lie groups and Lie algebras.
Representations of a finite group G are also linked directly to algebra representations via the group algebra
F[G], which is a vector space over F with the elements of G as a basis, equipped with the multiplication operation defined by the group operation, linearity, and the requirement that the group operation and scalar multiplication commute.
extended much of character theory to modular representations, and this theory played an important role in early progress towards the classification of finite simple groups
, especially for simple groups whose characterization was not amenable to purely group-theoretic methods because their Sylow 2-subgroups were "too small".
As well as having applications to group theory, modular representations arise naturally in other branches of mathematics
, such as algebraic geometry
, coding theory
, combinatorics
and number theory
.
V such that φ(g) is a unitary operator
for every g ∈ G. Such representations have been widely applied in quantum mechanics
since the 1920s, thanks in particular to the influence of Hermann Weyl
, and this has inspired the development of the theory, most notably through the analysis of representations of the Poincare group
by Eugene Wigner. One of the pioneers in constructing a general theory of unitary representations (for any group G rather than just for particular groups useful in applications) was George Mackey
, and an extensive theory was developed by Harish-Chandra
and others in the 1950s and 1960s.
A major goal is to describe the "unitary dual", the space of irreducible unitary representations of G. The theory is most well-developed in the case that G is a locally compact (Hausdorff) topological group
and the representations are strongly continuous. For G abelian, the unitary dual is just the space of characters
, while for G compact, the Peter-Weyl theorem shows that the irreducible unitary representations are finite dimensional and the unitary dual is discrete. For example, if G is the circle group S1, then the characters are given by integers, and the unitary dual is Z.
For non-compact G, the question of which representations are unitary is a subtle one. Although irreducible unitary representations must be "admissible" (as Harish-Chandra module
s) and it is easy to detect which admissible representations have a nondegenerate invariant sesquilinear form
, it is hard to determine when this form is positive definite. An effective description of the unitary dual, even for relatively well-behaved groups such as real reductive Lie group
s (discussed below), remains an important open problem in representation theory. It has been solved for many particular groups, such as SL(2,R)
and the Lorentz group.
, and the Fourier transform
similarly expresses the fact that the space of characters on a real vector space is the dual vector space. Thus unitary representation theory and harmonic analysis
are intimately related, and abstract harmonic analysis exploits this relationship, by developing the analysis
of functions on locally compact topological groups and related spaces.
A major goal is to provide a general form of the Fourier transform and the Plancherel theorem
. This is done by constructing a measure
on the unitary dual and an isomorphism between the regular representation of G on the space L2(G) of square integrable functions on G and its representation on the space of L2 functions on the unitary dual. Pontrjagin duality and the Peter-Weyl theorem achieve this for abelian and compact G respectively.
Another approach involves considering all unitary representations, not just the irreducible ones. These form a category
, and Tannaka-Krein duality
provides a way to recover a compact group from its category of unitary representations.
If the group is neither abelian nor compact, no general theory is known with an analogue of the Plancherel theorem or Fourier inversion, although Alexander Grothendieck
extended Tannaka-Krein duality to a relationship between linear algebraic group
s and tannakian categories
.
Harmonic analysis has also been extended from the analysis of functions on a group G to functions on homogeneous spaces for G. The theory is particularly well developed for symmetric space
s and provides a theory of automorphic form
s (discussed below).
is a group which is also a smooth manifold. Many classical groups of matrices over the real or complex numbers are Lie groups. Many of the groups important in physics and chemistry are Lie groups, and their representation theory is crucial to the application of group theory in those fields.
The representation theory of Lie groups can be developed first by considering the compact groups, to which results of compact representation theory apply. This theory can be extended to finite dimensional representations of semisimple Lie groups using Weyl's unitary trick: each semisimple real Lie group G has a complexification, which is a complex Lie group Gc, and this complex Lie group has a maximal compact subgroup K. The finite dimensional representations of G closely correspond to those of K.
A general Lie group is a semidirect product
of a solvable Lie group and a semisimple Lie group (the Levi decomposition
). The classification of representations of solvable Lie groups is intractable in general, but often easy in practical cases. Representations of semidirect products can then be analysed by means of general results called Mackey theory, which is a generalization of the methods used in Wigner's classification
of representations of the Poincaré group.
over a field F is a vector space over F equipped with a skew-symmetric bilinear operation called the Lie bracket
, which satisfies the Jacobi identity
. Lie algebras arise in particular as tangent space
s to Lie group
s at the identity element
, leading to their interpretation as "infinitesimal symmetries". An important approach to the representation theory of Lie groups is to study the corresponding representation theory of Lie algebras, but representations of Lie algebras also have an intrinsic interest.
Lie algebras, like Lie groups, have a Levi decomposition into semisimple and solvable parts, with the representation theory of solvable Lie algebras being intractable in general. In contrast, the finite dimensional representations of semisimple Lie algebras are completely understood, after work of Élie Cartan
. A representation of a semisimple Lie algebra g is analysed by choosing a Cartan subalgebra, which is essentially a generic maximal subalgebra h of g on which the Lie bracket is zero ("abelian"). The representation of g can be decomposed into weight spaces
which are eigenspaces for the action of h and the infinitesimal analogue of characters. The structure of semisimple Lie algebras then reduces the analysis of representations to easily understood combinatorics of the possible weights which can occur.
and Robert Moody
, who independently discovered them. These algebras form a generalization of finite-dimensional semisimple Lie algebras, and share many of their combinatorial properties. This means that they have a class of representations which can be understood in the same way as representations of semisimple Lie algebras.
Affine Lie algebras are a special case of Kac-Moody algebras which have particular importance in mathematics and theoretical physics
, especially conformal field theory
and the theory of exactly solvable models. Kac discovered an elegant proof of certain combinatorial identities, Macdonald identities
, which is based on the representation theory of affine Kac-Moody algebras.
s are generalizations of Lie algebras in which the underlying vector space has a Z2-grading, and skew-symmetry and Jacobi identity properties of the Lie bracket are modified by signs. Their representation theory is similar to the representation theory of Lie algebras.
s) are analogues in algebraic geometry of Lie group
s, but over more general fields than just R or C. In particular, over finite fields, they give rise to finite groups of Lie type. Although linear algebraic groups have a classification that is very similar to that of Lie groups, their representation theory is rather different (and much less well understood) and requires different techniques, since the Zariski topology
is relatively weak, and techniques from analysis are no longer available.
on algebraic varieties
from the point of view of their effect on functions, which form representations of the group. Classically, the theory dealt with the question of explicit description of polynomial functions that do not change, or are invariant, under the transformations from a given linear group. The modern approach analyses the decomposition of these representations into irreducibles.
Invariant theory of infinite group
s is inextricably linked with the development of linear algebra
, especially, the theories of quadratic form
s and determinant
s. Another subject with strong mutual influence is projective geometry
, where invariant theory can be used to organize the subject, and during the 1960s, new life was breathed into the subject by David Mumford
in the form of his geometric invariant theory
.
The representation theory of semisimple Lie groups has its roots in invariant theory and the strong links between representation theory and algebraic geometry have many parallels in differential geometry, beginning with Felix Klein
's Erlangen program
and Élie Cartan
's connections
, which place groups and symmetry at the heart of geometry. Modern developments link representation theory and invariant theory to areas as diverse as holonomy
, differential operator
s and the theory of several complex variables
.
s to more general analytic function
s, perhaps of several complex variables
, with similar transformation properties. The generalization involves replacing the modular group PSL2 (R) and a chosen congruence subgroup
by a semisimple Lie group G and a discrete subgroup Γ. Just as modular forms can be viewed as differential form
s on a quotient of the upper half space H = PSL2 (R)/SO(2), automorphic forms can be viewed as differential forms (or similar objects) on Γ\G/K, where K is (typically) a maximal compact subgroup
of G. Some care is required, however, as the quotient typically has singularities. The quotient of a semisimple Lie group by a compact subgroup is a symmetric space
and so the theory of automorphic forms is intimately related to harmonic analysis on symmetric spaces.
Before the development of the general theory, many important special cases were worked out in detail, including the Hilbert modular forms and Siegel modular form
s. Important results in the theory include the Selberg trace formula
and the realization by Robert Langlands
that the Riemann-Roch theorem could be applied to calculate the dimension of the space of automorphic forms. The subsequent notion of "automorphic representation" has proved of great technical value for dealing with the case that G is an algebraic group
, treated as an adelic algebraic group
. As a result an entire philosophy, the Langlands program
has developed around the relation between representation and number theoretic properties of automorphic forms.
representations generalize both representations of groups and Lie algebras. A representation of a group induces a representation of a corresponding group ring
or group algebra
, while representations of a Lie algebra correspond bijectively to representations of its universal enveloping algebra
. However, the representation theory of general associative algebras does not have all of the nice properties of the representation theory of groups and Lie algebras.
s provide a way to improve the representation theory of associative algebras, while retaining the representation theory of groups and Lie algebras as special cases. In particular, the tensor product of two representations is a representation, as is the dual vector space.
The Hopf algebras associated to groups have a commutative algebra structure, and so general Hopf algebras are known as quantum group
s, although this term is often restricted to certain Hopf algebras arising as deformations of groups or their universal enveloping algebras. The representation theory of quantum groups has added surprising insights to the representation theory of Lie groups and Lie algebras, for instance through the crystal basis of Kashiwara.
or permutation representation) of a group
G on a set X is given by a function
ρ from G to XX, the set of function
s from X to X, such that for all g1, g2 in G and all x in X:


This condition and the axioms for a group imply that ρ(g) is a bijection
(or permutation
) for all g in G. Thus we may equivalently define a permutation representation to be a group homomorphism
from G to the symmetric group
SX of X.
with a single object; morphism
s in this category are just the elements of G. Given an arbitrary category C, a representation of G in C is a functor
from G to C. Such a functor selects an object X in C and a group homomorphism from G to Aut(X), the automorphism group of X.
In the case where C is VectF, the category of vector spaces
over a field F, this definition is equivalent to a linear representation. Likewise, a set-theoretic representation is just a representation of G in the category of sets
.
For another example consider the category of topological spaces
, Top. Representations in Top are homomorphisms from G to the homeomorphism
group of a topological space X.
Two types of representations closely related to linear representations are:
s, which are categories with one object. Groups are monoids for which every morphism is invertible. General monoids have representations in any category. In the category of sets, these are monoid actions, but monoid representations on vector spaces and other objects can be studied.
More generally, one can relax the assumption that the category being represented has only one object. In full generality, this is simply the theory of functor
s between categories, and little can be said.
One special case has had a significant impact on representation theory, namely the representation theory of quivers. A quiver is simply a directed graph
(with loops and multiple arrows allowed), but it can be made into a category (and also an algebra) by considering paths in the graph. Representations of such categories/algebras have illuminated several aspects of representation theory, for instance by allowing non-semisimple representation theory questions about a group to be reduced in some cases to semisimple representation theory questions about a quiver.
Specific applications
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
that studies abstract
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s by representing their elements as linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s of vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s, and studies
modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over these abstract algebraic structures. In essence, a representation makes an abstract algebraic object more concrete by describing its elements by matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
and the algebraic operations in terms of matrix addition
Matrix addition
In mathematics, matrix addition is the operation of adding two matrices by adding the corresponding entries together. However, there are other operations which could also be considered as a kind of addition for matrices, the direct sum and the Kronecker sum....
and matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
. The algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
ic objects amenable to such a description include groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
s and Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s. The most prominent of these (and historically the first) is the representation theory of groups
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
, in which elements of a group are represented by invertible matrices in such a way that the group operation is matrix multiplication.
Representation theory is a powerful tool because it reduces problems in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
to problems in linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a subject which is well understood. Furthermore, the vector space on which a group (for example) is represented can be infinite dimensional, and by allowing it to be, for instance, a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, methods of analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
can be applied to the theory of groups. Representation theory is also important in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
because, for example, it describes how the symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of a physical system affects the solutions of equations describing that system.
A striking feature of representation theory is its pervasiveness in mathematics. There are two sides to this. First, the applications of representation theory are diverse: in addition to its impact on algebra, representation theory illuminates and vastly generalizes Fourier analysis via harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
, is deeply connected to geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
via invariant theory
Invariant theory
Invariant theory is a branch of abstract algebra dealing with actions of groups on algebraic varieties from the point of view of their effect on functions...
and the Erlangen program
Erlangen program
An influential research program and manifesto was published in 1872 by Felix Klein, under the title Vergleichende Betrachtungen über neuere geometrische Forschungen...
, and has a profound impact in number theory via automorphic form
Automorphic form
In mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
s and the Langlands program
Langlands program
The Langlands program is a web of far-reaching and influential conjectures that relate Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups over local fields and adeles. It was proposed by ....
. The second aspect is the diversity of approaches to representation theory. The same objects can be studied using methods from algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, module theory, analytic number theory
Analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
, differential geometry, operator theory
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
and topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
.
The success of representation theory has led to numerous generalizations. One of the most general is a categorical one
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
. The algebraic objects to which representation theory applies can be viewed as particular kinds of categories, and the representations as functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s from the object category to the category of vector spaces
Category of vector spaces
In mathematics, especially category theory, the category K-Vect has all vector spaces over a fixed field K as objects and K-linear transformations as morphisms...
. This description points to two obvious generalizations: first, the algebraic objects can be replaced by more general categories; second the target category of vector spaces can be replaced by other well-understood categories.
Definitions and concepts
Let V be a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F. For instance, suppose V is Rn or Cn, the standard n-dimensional space of column vectors over the real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s respectively. In this case, the idea of representation theory is to do abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
concretely by using n × n matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
of real or complex numbers.
There are three main sorts of algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
ic objects for which this can be done: groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
s and Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s.
- The set of all invertible n × n matrices is a group under matrix multiplicationMatrix multiplicationIn mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
and the representation theory of groupsGroup representationIn the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
analyses a group by describing ("representing") its elements in terms of invertible matrices. - Matrix addition and multiplication make the set of all n × n matrices into an associative algebra and hence there is a corresponding representation theory of associative algebras.
- If we replace matrix multiplication MN by the matrix commutatorCommutatorIn mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
MN − NM, then the n × n matrices become instead a Lie algebra, leading to a representation theory of Lie algebrasRepresentation of a Lie algebraIn the mathematical field of representation theory, a Lie algebra representation or representation of a Lie algebra is a way of writing a Lie algebra as a set of matrices in such a way that the Lie bracket is given by the commutator.The notion is closely related to that of a representation of a...
.
This generalizes to any field F and any vector space V over F, with linear maps replacing matrices and composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
replacing matrix multiplication: there is a group GL(V,F) of automorphisms of V, an associative algebra EndF(V) of all endomorphisms of V, and a corresponding Lie algebra gl(V,F).
Definition
There are two ways to say what a representation is. The first uses the idea of an actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
, generalizing the way that matrices act on column vectors by matrix multiplication. A representation of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G or (associative or Lie) algebra A on a vector space V is a map
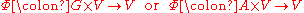
with two properties. First, for any g in G (or a in A), the map
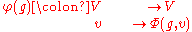
is linear (over F), and similarly in the algebra cases. Second, if we introduce the notation g · v for Φ (g, v), then for any g1, g2 in G and v in V:
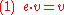
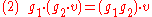
where e is the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
of G and g1g2 is product in G. The requirement for associative algebras is analogous, except that associative algebras do not always have an identity element, in which case equation (1) is ignored. Equation (2) is an abstract expression of the associativity of matrix multiplication. This doesn't hold for the matrix commutator and also there is no identity element for the commutator. Hence for Lie algebras, the only requirement is that for any x1, x2 in A and v in V:

where [x1, x2] is the Lie bracket
Lie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
, which generalizes the matrix commutator MN − NM.
The second way to define a representation focuses on the map φ sending g in G to φ(g): V → V, which satisfies
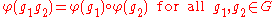
and similarly in the other cases. This approach is both more concise and more abstract.
- A representation of a group G on a vector space V is a group homomorphismGroup homomorphismIn mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
φ: G → GL(V,F). - A representation of an associative algebra A on a vector space V is an algebra homomorphismAlgebra homomorphismA homomorphism between two algebras, A and B, over a field K, is a map F:A\rightarrow B such that for all k in K and x,y in A,* F = kF* F = F + F...
φ: A → EndF(V). - A representation of a Lie algebra a on a vector space V is a Lie algebra homomorphism φ: a → gl(V,F).
Terminology
The vector space V is called the representation space of φ and its dimension (if finite) is called the dimension of the representation (sometimes degree, as in ). It is also common practice to refer to V itself as the representation when the homomorphism φ is clear from the context; otherwise the notation (V,φ) can be used to denote a representation.When V is of finite dimension n, one can choose a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for V to identify V with Fn and hence recover a matrix representation with entries in the field F.
An effective or faithful representation
Faithful representation
In mathematics, especially in the area of abstract algebra known as representation theory, a faithful representation ρ of a group G on a vector space V is a linear representation in which different elements g of G are represented by distinct linear mappings ρ.In more abstract language, this means...
is a representation (V,φ) for which the homomorphism φ is injective.
Equivariant maps and isomorphisms
If V and W are vector spaces over F, equipped with representations φ and ψ of a group G, then an equivariant map from V to W is linear map α: V → W such that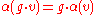
for all g in G and v in V. In terms of φ: G → GL(V) and ψ: G → GL(W), this means
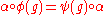
for all g in G.
Equivariant maps for representations of an associative or Lie algebra are defined similarly. If α is invertible, then it is said to be an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
, in which case V and W (or, more precisely, φ and ψ) are isomorphic representations.
Isomorphic representations are, for all practical purposes, "the same": they provide the same information about the group or algebra being represented. Representation theory therefore seeks to classify representations "up to isomorphism".
Subrepresentations, quotients, and irreducible representations
If (W,ψ) is a representation of (say) a group G, and V is a linear subspace of W which is preserved by the action of G in the sense that g · v ∈ V for all v ∈ V (Serre calls these V stable under G), then V is called a subrepresentation: by defining φ(g) to be the restriction of ψ(g) to V, (V, φ) is a representation of G and the inclusion of V into W is an equivariant map. The quotient spaceQuotient space (linear algebra)
In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
W/V can also be made into a representation of G.
If W has exactly two subrepresentations, namely the trivial subspace {0} and W itself, then the representation is said to be irreducible; if W has a proper nontrivial subrepresentation, the representation is said to be reducible.
The definition of an irreducible representation implies Schur's lemma
Schur's lemma
In mathematics, Schur's lemma is an elementary but extremely useful statement in representation theory of groups and algebras. In the group case it says that if M and N are two finite-dimensional irreducible representations...
: an equivariant map α: V → W between irreducible representations is either the zero map or an isomorphism, since its kernel and image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
are subrepresentations. In particular, when V = W, this shows that the equivariant endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
s of V form an associative division algebra
Division algebra
In the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field, in which division is possible.- Definitions :...
over the underlying field F. If F is algebraically closed, the only equivariant endomorphisms of an irreducible representation are the scalar multiples of the identity.
Irreducible representations are the building blocks of representation theory: if a representation W is not irreducible then it is built from a subrepresentation and a quotient which are both "simpler" in some sense; for instance, if W is finite dimensional, then both the subrepresentation and the quotient have smaller dimension.
Direct sums and indecomposable representations
If (V,φ) and (W,ψ) are representations of (say) a group G, then the direct sum of V and W is a representation, in a canonical way, via the equation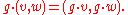
The direct sum of two representations carries no more information about the group G than the two representations do individually. If a representation is the direct sum of two proper nontrivial subrepresentations, it is said to be decomposable. Otherwise, it is said to be indecomposable.
In favourable circumstances, every representation is a direct sum of irreducible representations: such representations are said to be semisimple. In this case, it suffices to understand only the irreducible representations. In other cases, one must understand how indecomposable representations can be built from irreducible representations as extensions of a quotient by a subrepresentation.
Branches and topics
Representation theory is notable for the number of branches it has, and the diversity of the approaches to studying representations of groups and algebras. Although, all the theories have in common the basic concepts discussed already, they differ considerably in detail. The differences are at least 3-fold:- Representation theory depends upon the type of algebraic object being represented. There are several different classes of groups, associative algebras and Lie algebras, and their representation theories all have an individual flavour.
- Representation theory depends upon the nature of the vector space on which the algebraic object is represented. The most important distinction is between finite dimensionalDimension (vector space)In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
representations and infinite dimensional ones. In the infinite-dimensional case, additional structures are important (e.g. whether or not the space is a Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
, etc.). Additional algebraic structures can also be imposed in the finite dimensional case. - Representation theory depends upon the type of fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
over which the vector space is defined. The most important case is the field of complex numbers. The other important cases are the field of real numbers, finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s, and fields of p-adic numberP-adic numberIn mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
s. Additional difficulties arise for fields of positive characteristic and for fields which are not algebraically closed.
Finite groups
Group representations are a very important tool in the study of finite groups. They also arise in the applications of finite group theory to geometry and crystallography. Representations of finite groups exhibit many of the features of the general theory and point the way to other branches and topics in representation theory.Over a field of characteristic zero, the representation theory of a finite group G has a number of convenient properties. First, the representations of G are semisimple (completely reducible). This is a consequence of Maschke's theorem
Maschke's theorem
In mathematics, Maschke's theorem, named after Heinrich Maschke, is a theorem in group representation theory that concerns the decomposition of representations of a finite group into irreducible pieces...
, which states that any subrepresentation V of a G-representation W has a G-invariant complement. One proof is to choose any projection
Projection (linear algebra)
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself such that P2 = P. It leaves its image unchanged....
π from W to V and replace it by its average
Average
In mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....
πG defined by

πG is equivariant, and its kernel is the required complement.
The finite dimensional G-representations can be understood using character theory
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
: the character of a representation φ: G → GL(V) is the class function χφ: G → F defined by
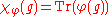
where
 is the trace. An irreducible representation of G is completely determined by its character.
is the trace. An irreducible representation of G is completely determined by its character.Maschke's theorem holds more generally for fields of positive characteristic p, such as the finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s, as long as the prime p is coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to the order of G. When p and |G| have a common factor, there are G-representations which are not semisimple, which are studied in a subbranch called modular representation theory
Modular representation theory
Modular representation theory is a branch of mathematics, and that part of representation theory that studies linear representations of finite group G over a field K of positive characteristic...
.
Averaging techniques also show that if F is the real or complex numbers, then any G-representation preserves an inner product
 on V in the sense that
on V in the sense that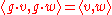
for all g in G and v, w in W. Hence any G-representation is unitary
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
.
Unitary representations are automatically semisimple, since Maschke's result can be proven by taking the orthogonal complement of a subrepresentation. When studying representations of groups which are not finite, the unitary representations provide a good generalization of the real and complex representations of a finite group.
Results such as Maschke's theorem and the unitary property which rely on averaging can be generalized to more general groups by replacing the average with an integral, provided that a suitable notion of integral can be defined. This can be done for compact group
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
s or locally compact group
Locally compact group
In mathematics, a locally compact group is a topological group G which is locally compact as a topological space. Locally compact groups are important because they have a natural measure called the Haar measure. This allows one to define integrals of functions on G.Many of the results of finite...
s, using Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
, and the resulting theory is known as abstract harmonic analysis.
Over arbitrary fields, another class of finite groups which have a good representation theory are the finite groups of Lie type. Important examples are linear algebraic group
Linear algebraic group
In mathematics, a linear algebraic group is a subgroup of the group of invertible n×n matrices that is defined by polynomial equations...
s over finite fields. The representation theory of linear algebraic groups and Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s extends these examples to infinite dimensional groups, the latter being intimately related to Lie algebra representations. The importance of character theory for finite groups has an analogue in the theory of weights
Weight (representation theory)
In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F – a linear functional – or equivalently, a one dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group...
for representations of Lie groups and Lie algebras.
Representations of a finite group G are also linked directly to algebra representations via the group algebra
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
F[G], which is a vector space over F with the elements of G as a basis, equipped with the multiplication operation defined by the group operation, linearity, and the requirement that the group operation and scalar multiplication commute.
Modular representations
Modular representations of a finite group G are representations over a field whose characteristic is not coprime to |G|, so that Maschke's theorem no longer holds (because |G| is not invertible in F and so one cannot divide by it). Nevertheless, Richard BrauerRichard Brauer
Richard Dagobert Brauer was a leading German and American mathematician. He worked mainly in abstract algebra, but made important contributions to number theory...
extended much of character theory to modular representations, and this theory played an important role in early progress towards the classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
, especially for simple groups whose characterization was not amenable to purely group-theoretic methods because their Sylow 2-subgroups were "too small".
As well as having applications to group theory, modular representations arise naturally in other branches of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, such as algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, coding theory
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
.
Unitary representations
A unitary representation of a group G is a linear representation φ of G on a real or (usually) complex Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
V such that φ(g) is a unitary operator
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
for every g ∈ G. Such representations have been widely applied in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
since the 1920s, thanks in particular to the influence of Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
, and this has inspired the development of the theory, most notably through the analysis of representations of the Poincare group
Representation theory of the Poincaré group
In mathematics, the representation theory of the Poincaré group is an example of the representation theory of a Lie group that is neither a compact group nor a semisimple group. It is fundamental in theoretical physics....
by Eugene Wigner. One of the pioneers in constructing a general theory of unitary representations (for any group G rather than just for particular groups useful in applications) was George Mackey
George Mackey
George Whitelaw Mackey was an American mathematician. Mackey earned his bachelor of arts at Rice University in 1938 and obtained his Ph.D. at Harvard University in 1942 under the direction of Marshall H. Stone...
, and an extensive theory was developed by Harish-Chandra
Harish-Chandra
Harish-Chandra was an Indian mathematician, who did fundamental work in representation theory, especially Harmonic analysis on semisimple Lie groups. -Life:...
and others in the 1950s and 1960s.
A major goal is to describe the "unitary dual", the space of irreducible unitary representations of G. The theory is most well-developed in the case that G is a locally compact (Hausdorff) topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
and the representations are strongly continuous. For G abelian, the unitary dual is just the space of characters
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
, while for G compact, the Peter-Weyl theorem shows that the irreducible unitary representations are finite dimensional and the unitary dual is discrete. For example, if G is the circle group S1, then the characters are given by integers, and the unitary dual is Z.
For non-compact G, the question of which representations are unitary is a subtle one. Although irreducible unitary representations must be "admissible" (as Harish-Chandra module
Harish-Chandra module
In mathematics, specifically in the representation theory of Lie groups, a Harish-Chandra module is a representation of a real Lie group, associated to a general representation, with regularity and finiteness conditions...
s) and it is easy to detect which admissible representations have a nondegenerate invariant sesquilinear form
Sesquilinear form
In mathematics, a sesquilinear form on a complex vector space V is a map V × V → C that is linear in one argument and antilinear in the other. The name originates from the numerical prefix sesqui- meaning "one and a half"...
, it is hard to determine when this form is positive definite. An effective description of the unitary dual, even for relatively well-behaved groups such as real reductive Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s (discussed below), remains an important open problem in representation theory. It has been solved for many particular groups, such as SL(2,R)
Representation theory of SL2(R)
In mathematics, the main results concerning irreducible unitary representations of the Lie group SL are due to Gelfand and Naimark , V...
and the Lorentz group.
Harmonic analysis
The duality between the circle group S1 and the integers Z, or more generally, between a torus Tn and Zn is well known in analysis as the theory of Fourier seriesFourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
, and the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
similarly expresses the fact that the space of characters on a real vector space is the dual vector space. Thus unitary representation theory and harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
are intimately related, and abstract harmonic analysis exploits this relationship, by developing the analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
of functions on locally compact topological groups and related spaces.
A major goal is to provide a general form of the Fourier transform and the Plancherel theorem
Plancherel theorem
In mathematics, the Plancherel theorem is a result in harmonic analysis, proved by Michel Plancherel in 1910. It states that the integral of a function's squared modulus is equal to the integral of the squared modulus of its frequency spectrum....
. This is done by constructing a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on the unitary dual and an isomorphism between the regular representation of G on the space L2(G) of square integrable functions on G and its representation on the space of L2 functions on the unitary dual. Pontrjagin duality and the Peter-Weyl theorem achieve this for abelian and compact G respectively.
Another approach involves considering all unitary representations, not just the irreducible ones. These form a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
, and Tannaka-Krein duality
Tannaka-Krein duality
In mathematics, Tannaka–Krein duality theory concerns the interaction of a compact topological group and its category of linear representations. Its natural extension to the non-Abelian case is the Grothendieck duality theory....
provides a way to recover a compact group from its category of unitary representations.
If the group is neither abelian nor compact, no general theory is known with an analogue of the Plancherel theorem or Fourier inversion, although Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
extended Tannaka-Krein duality to a relationship between linear algebraic group
Linear algebraic group
In mathematics, a linear algebraic group is a subgroup of the group of invertible n×n matrices that is defined by polynomial equations...
s and tannakian categories
Tannakian category
In mathematics, a tannakian category is a particular kind of monoidal category C, equipped with some extra structure relative to a given field K. The role of such categories C is to approximate, in some sense, the category of linear representations of an algebraic group G defined over K...
.
Harmonic analysis has also been extended from the analysis of functions on a group G to functions on homogeneous spaces for G. The theory is particularly well developed for symmetric space
Symmetric space
A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
s and provides a theory of automorphic form
Automorphic form
In mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
s (discussed below).
Lie groups
A Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
is a group which is also a smooth manifold. Many classical groups of matrices over the real or complex numbers are Lie groups. Many of the groups important in physics and chemistry are Lie groups, and their representation theory is crucial to the application of group theory in those fields.
The representation theory of Lie groups can be developed first by considering the compact groups, to which results of compact representation theory apply. This theory can be extended to finite dimensional representations of semisimple Lie groups using Weyl's unitary trick: each semisimple real Lie group G has a complexification, which is a complex Lie group Gc, and this complex Lie group has a maximal compact subgroup K. The finite dimensional representations of G closely correspond to those of K.
A general Lie group is a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of a solvable Lie group and a semisimple Lie group (the Levi decomposition
Levi decomposition
In Lie theory and representation theory, the Levi decomposition, conjectured by Killing and Cartan and proved by , states that any finite dimensional real Lie algebra g is the semidirect product of a solvable ideal and a semisimple subalgebra....
). The classification of representations of solvable Lie groups is intractable in general, but often easy in practical cases. Representations of semidirect products can then be analysed by means of general results called Mackey theory, which is a generalization of the methods used in Wigner's classification
Wigner's classification
In mathematics and theoretical physics, Wigner's classificationis a classification of the nonnegative energy irreducible unitary representations of the Poincaré group, which have sharp mass eigenvalues...
of representations of the Poincaré group.
Lie algebras
A Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
over a field F is a vector space over F equipped with a skew-symmetric bilinear operation called the Lie bracket
Lie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
, which satisfies the Jacobi identity
Jacobi identity
In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
. Lie algebras arise in particular as tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
s to Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s at the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
, leading to their interpretation as "infinitesimal symmetries". An important approach to the representation theory of Lie groups is to study the corresponding representation theory of Lie algebras, but representations of Lie algebras also have an intrinsic interest.
Lie algebras, like Lie groups, have a Levi decomposition into semisimple and solvable parts, with the representation theory of solvable Lie algebras being intractable in general. In contrast, the finite dimensional representations of semisimple Lie algebras are completely understood, after work of Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
. A representation of a semisimple Lie algebra g is analysed by choosing a Cartan subalgebra, which is essentially a generic maximal subalgebra h of g on which the Lie bracket is zero ("abelian"). The representation of g can be decomposed into weight spaces
Weight (representation theory)
In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F – a linear functional – or equivalently, a one dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group...
which are eigenspaces for the action of h and the infinitesimal analogue of characters. The structure of semisimple Lie algebras then reduces the analysis of representations to easily understood combinatorics of the possible weights which can occur.
Infinite dimensional Lie algebras
There are many classes of infinite dimensional Lie algebras whose representations have been studied. Among these, an important class are the Kac-Moody algebras. They are named after Victor KacVictor Kac
Victor G. Kac is a Soviet and American mathematician at MIT, known for his work in representation theory. He discovered Kac–Moody algebras, and used the Weyl–Kac character formula for them to reprove the Macdonald identities...
and Robert Moody
Robert Moody
Robert Vaughan Moody, OC, FRSC is a Canadian mathematician. He is the co-discover of Kac-Moody algebra, a Lie algebra, usually infinite-dimensional, that can be defined through a generalized root system....
, who independently discovered them. These algebras form a generalization of finite-dimensional semisimple Lie algebras, and share many of their combinatorial properties. This means that they have a class of representations which can be understood in the same way as representations of semisimple Lie algebras.
Affine Lie algebras are a special case of Kac-Moody algebras which have particular importance in mathematics and theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, especially conformal field theory
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
and the theory of exactly solvable models. Kac discovered an elegant proof of certain combinatorial identities, Macdonald identities
Macdonald identities
In mathematics, the Macdonald identities are some infinite product identities associated to affine root systems, introduced by . They include as special cases the Jacobi triple product identity, Watson's quintuple product identity, several identities found by , and a 10-fold product identity found...
, which is based on the representation theory of affine Kac-Moody algebras.
Lie superalgebras
Lie superalgebraLie superalgebra
In mathematics, a Lie superalgebra is a generalisation of a Lie algebra to include a Z2-grading. Lie superalgebras are important in theoretical physics where they are used to describe the mathematics of supersymmetry...
s are generalizations of Lie algebras in which the underlying vector space has a Z2-grading, and skew-symmetry and Jacobi identity properties of the Lie bracket are modified by signs. Their representation theory is similar to the representation theory of Lie algebras.
Linear algebraic groups
Linear algebraic groups (or more generally, affine group schemeGroup scheme
In mathematics, a group scheme is a type of algebro-geometric object equipped with a composition law. Group schemes arise naturally as symmetries of schemes, and they generalize algebraic groups, in the sense that all algebraic groups have group scheme structure, but group schemes are not...
s) are analogues in algebraic geometry of Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s, but over more general fields than just R or C. In particular, over finite fields, they give rise to finite groups of Lie type. Although linear algebraic groups have a classification that is very similar to that of Lie groups, their representation theory is rather different (and much less well understood) and requires different techniques, since the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
is relatively weak, and techniques from analysis are no longer available.
Invariant theory
Invariant theory studies actionsGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on algebraic varieties
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
from the point of view of their effect on functions, which form representations of the group. Classically, the theory dealt with the question of explicit description of polynomial functions that do not change, or are invariant, under the transformations from a given linear group. The modern approach analyses the decomposition of these representations into irreducibles.
Invariant theory of infinite group
Infinite group
In group theory, an area of mathematics, an infinite group is a group, of which the underlying set contains an infinite number of elements....
s is inextricably linked with the development of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, especially, the theories of quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s and determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
s. Another subject with strong mutual influence is projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
, where invariant theory can be used to organize the subject, and during the 1960s, new life was breathed into the subject by David Mumford
David Mumford
David Bryant Mumford is an American mathematician known for distinguished work in algebraic geometry, and then for research into vision and pattern theory. He won the Fields Medal and was a MacArthur Fellow. In 2010 he was awarded the National Medal of Science...
in the form of his geometric invariant theory
Geometric invariant theory
In mathematics Geometric invariant theory is a method for constructing quotients by group actions in algebraic geometry, used to construct moduli spaces...
.
The representation theory of semisimple Lie groups has its roots in invariant theory and the strong links between representation theory and algebraic geometry have many parallels in differential geometry, beginning with Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
's Erlangen program
Erlangen program
An influential research program and manifesto was published in 1872 by Felix Klein, under the title Vergleichende Betrachtungen über neuere geometrische Forschungen...
and Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
's connections
Cartan connection
In the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the...
, which place groups and symmetry at the heart of geometry. Modern developments link representation theory and invariant theory to areas as diverse as holonomy
Holonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
, differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s and the theory of several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
.
Automorphic forms and number theory
Automorphic forms are a generalization of modular formModular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s to more general analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s, perhaps of several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
, with similar transformation properties. The generalization involves replacing the modular group PSL2 (R) and a chosen congruence subgroup
Congruence subgroup
In mathematics, a congruence subgroup of a matrix group with integer entries is a subgroup defined by congruence conditions on the entries. A very simple example would be invertible 2x2 integer matrices of determinant 1, such that the off-diagonal entries are even.An importance class of congruence...
by a semisimple Lie group G and a discrete subgroup Γ. Just as modular forms can be viewed as differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s on a quotient of the upper half space H = PSL2 (R)/SO(2), automorphic forms can be viewed as differential forms (or similar objects) on Γ\G/K, where K is (typically) a maximal compact subgroup
Maximal compact subgroup
In mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
of G. Some care is required, however, as the quotient typically has singularities. The quotient of a semisimple Lie group by a compact subgroup is a symmetric space
Symmetric space
A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
and so the theory of automorphic forms is intimately related to harmonic analysis on symmetric spaces.
Before the development of the general theory, many important special cases were worked out in detail, including the Hilbert modular forms and Siegel modular form
Siegel modular form
In mathematics, Siegel modular forms are a major type of automorphic form. These stand in relation to the conventional elliptic modular forms as abelian varieties do in relation to elliptic curves; the complex manifolds constructed as in the theory are basic models for what a moduli space for...
s. Important results in the theory include the Selberg trace formula
Selberg trace formula
In mathematics, the Selberg trace formula, introduced by , is an expression for the character of the unitary representation of G on the space L2 of square-integrable functions, where G is a Lie group and Γ a cofinite discrete group...
and the realization by Robert Langlands
Robert Langlands
Robert Phelan Langlands is a mathematician, best known as the founder of the Langlands program. He is an emeritus professor at the Institute for Advanced Study...
that the Riemann-Roch theorem could be applied to calculate the dimension of the space of automorphic forms. The subsequent notion of "automorphic representation" has proved of great technical value for dealing with the case that G is an algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
, treated as an adelic algebraic group
Adelic algebraic group
In abstract algebra, an adelic algebraic group is a topological group defined by an algebraic group G over a number field K, and the adele ring A = A of K. It consists of the points of G having values in A; the definition of the appropriate topology is straightforward only in case G is a linear...
. As a result an entire philosophy, the Langlands program
Langlands program
The Langlands program is a web of far-reaching and influential conjectures that relate Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups over local fields and adeles. It was proposed by ....
has developed around the relation between representation and number theoretic properties of automorphic forms.
Associative algebras
In one sense, associative algebraAssociative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
representations generalize both representations of groups and Lie algebras. A representation of a group induces a representation of a corresponding group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
or group algebra
Group algebra
In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
, while representations of a Lie algebra correspond bijectively to representations of its universal enveloping algebra
Universal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
. However, the representation theory of general associative algebras does not have all of the nice properties of the representation theory of groups and Lie algebras.
Module theory
When considering representations of an associative algebra, one can forget the underlying field, and simply regard the associative algebra as a ring, and its representations as modules. This approach is surprisingly fruitful: many results in representation theory can be interpreted as special cases of results about modules over a ring.Hopf algebras and quantum groups
Hopf algebraHopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
s provide a way to improve the representation theory of associative algebras, while retaining the representation theory of groups and Lie algebras as special cases. In particular, the tensor product of two representations is a representation, as is the dual vector space.
The Hopf algebras associated to groups have a commutative algebra structure, and so general Hopf algebras are known as quantum group
Quantum group
In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
s, although this term is often restricted to certain Hopf algebras arising as deformations of groups or their universal enveloping algebras. The representation theory of quantum groups has added surprising insights to the representation theory of Lie groups and Lie algebras, for instance through the crystal basis of Kashiwara.
Set-theoretical representations
A set-theoretic representation (also known as a group actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
or permutation representation) of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G on a set X is given by a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
ρ from G to XX, the set of function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s from X to X, such that for all g1, g2 in G and all x in X:


This condition and the axioms for a group imply that ρ(g) is a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
(or permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
) for all g in G. Thus we may equivalently define a permutation representation to be a group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
from G to the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
SX of X.
Representations in other categories
Every group G can be viewed as a categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
with a single object; morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s in this category are just the elements of G. Given an arbitrary category C, a representation of G in C is a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from G to C. Such a functor selects an object X in C and a group homomorphism from G to Aut(X), the automorphism group of X.
In the case where C is VectF, the category of vector spaces
Category of vector spaces
In mathematics, especially category theory, the category K-Vect has all vector spaces over a fixed field K as objects and K-linear transformations as morphisms...
over a field F, this definition is equivalent to a linear representation. Likewise, a set-theoretic representation is just a representation of G in the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
.
For another example consider the category of topological spaces
Category of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
, Top. Representations in Top are homomorphisms from G to the homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
group of a topological space X.
Two types of representations closely related to linear representations are:
- projective representationProjective representationIn the mathematical field of representation theory, a projective representation of a group G on a vector space V over a field F is a group homomorphism from G to the projective linear groupwhere GL is the general linear group of invertible linear transformations of V over F and F* here is the...
s: in the category of projective spaceProjective spaceIn mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
s. These can be described as "linear representations up toUp toIn mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
scalar transformations". - affine representationAffine representationAn affine representation of a topological group G on an affine space A is a continuous group homomorphism from G to the automorphism group of A, the affine group Aff...
s: in the category of affine spaceAffine spaceIn mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
s. For example, the Euclidean groupEuclidean groupIn mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
acts affinely upon Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
.
Representations of categories
Since groups are categories, one can also consider representation of other categories. The simplest generalization is to monoidMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
s, which are categories with one object. Groups are monoids for which every morphism is invertible. General monoids have representations in any category. In the category of sets, these are monoid actions, but monoid representations on vector spaces and other objects can be studied.
More generally, one can relax the assumption that the category being represented has only one object. In full generality, this is simply the theory of functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s between categories, and little can be said.
One special case has had a significant impact on representation theory, namely the representation theory of quivers. A quiver is simply a directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
(with loops and multiple arrows allowed), but it can be made into a category (and also an algebra) by considering paths in the graph. Representations of such categories/algebras have illuminated several aspects of representation theory, for instance by allowing non-semisimple representation theory questions about a group to be reduced in some cases to semisimple representation theory questions about a quiver.
See also
General topics- Philosophy of sciencePhilosophy of scienceThe philosophy of science is concerned with the assumptions, foundations, methods and implications of science. It is also concerned with the use and merit of science and sometimes overlaps metaphysics and epistemology by exploring whether scientific results are actually a study of truth...
- List of representation theory topics
- List of harmonic analysis topics
Specific applications
- Geographic information scienceGeographic Information ScienceGeographic information science is the academic theory behind the development, use, and application of geographic information systems...
- Spatial autocorrelation
- Complete spatial randomnessComplete spatial randomnessComplete spatial randomness describes a point process whereby point events occur within a given study area in a completely random fashion. Such a process is often modeled using only one parameter, i.e. the density of points, \rho within the defined area...
- Modifiable Areal Unit ProblemModifiable Areal Unit ProblemThe modifiable areal unit problem is a source of statistical bias that can radically affect the results of statistical hypothesis tests. It affects results when point-based measures of spatial phenomena are aggregated into districts. The resulting summary values are influenced by the choice of...
- Symmetrica (public domain software)

