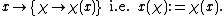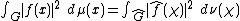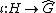Pontryagin duality
Encyclopedia
In mathematics, specifically in harmonic analysis
and the theory of topological group
s, Pontryagin duality explains the general properties of the Fourier transform
on locally compact groups, such as R, the circle or finite cyclic groups.
The theory, introduced by Lev Pontryagin and combined with Haar measure
introduced by John von Neumann
, André Weil
and others depends on the theory of the dual group of a locally compact
abelian group.
It is analogous to the dual vector space of a finite-dimensional vector space: a vector space V and its dual vector space V* are not naturally isomorphic, but their endomorphism algebras (matrix algebras) are: End(V) via the transpose. Similarly, a group G and its dual group
via the transpose. Similarly, a group G and its dual group 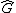 are not in general isomorphic, but their group algebra
are not in general isomorphic, but their group algebra
s are: C(G) via the Fourier transform, though one must carefully define these algebras analytically. More categorically, this is not just an isomorphism of endomorphism algebras, but an isomorphism of categories – see categorical considerations.
via the Fourier transform, though one must carefully define these algebras analytically. More categorically, this is not just an isomorphism of endomorphism algebras, but an isomorphism of categories – see categorical considerations.
is locally compact
if and only if the identity e of the group has a compact neighborhood. This means that there is some open set V containing e whose closure is compact in the topology of G. One of the most remarkable facts about a locally compact group G is that it carries an essentially unique natural measure
, the Haar measure
, which allows one to consistently measure the "size" of sufficiently regular subsets of G. "Sufficiently regular subset" here means a Borel set
; that is, an element of the σ-algebra
generated by the compact sets. More precisely, a right Haar measure on a locally compact group G is a countably additive measure μ defined on the Borel sets of G which is right invariant in the sense that μ(A x) = μ(A) for x an element of G and A a Borel subset of G and also satisfies some regularity conditions (spelled out in detail in the article on Haar measure
). Except for positive scaling factors, a Haar measure on G is unique.
The Haar measure on G allows us to define the notion of integral
for (complex
-valued) Borel functions defined on the group. In particular, one may consider various Lp spaces associated to the Haar measure. Specifically,
Note that, since any two Haar measures on G are equal up to a scaling factor, this Lp-space is independent of the choice
of Haar measure and thus perhaps could be written as Lp(G). However, the Lp-norm on this space
depends on the choice of Haar measure, so if one wants to talk about isometries it is important to keep track of the Haar measure being used.
Examples of locally compact abelian
groups are:
of G is a continuous group homomorphism
from G with values in the circle group T. The set of all characters on G can be made into a locally compact abelian group, called the dual group of G and denoted Ĝ. The group operation on the dual group is given by pointwise multiplication of characters, the inverse of a character is its complex conjugate and the topology
on the space of characters is that of uniform convergence on compact sets (i.e., the compact-open topology
, viewing Ĝ as a subset of the space of all continuous functions from G to T.). This topology in general is not metrizable. However, if the group G is a separable locally compact abelian group, then the dual group is metrizable.
This is analogous to the dual space
in linear algebra: just as for a vector space V over a field K, the dual space is
so too is the dual group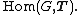 More abstractly, these are both examples of representable functor
More abstractly, these are both examples of representable functor
s, being represented respectively by K and T.
Canonical
means that there is a naturally defined map from G into (G^)^; more importantly, the map should be functorial. The canonical isomorphism is defined as follows:
In other words, each group element x is identified to the evaluation character on the dual. This is exactly the same as the canonical isomorphism between a finite-dimensional vector space and its double dual,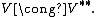 However, there is also a difference: V is isomorphic to its dual space V*, although not canonically so, while many groups G are not isomorphic to their dual groups (for instance, when G is T its dual is Z, and T is not isomorphic to Z as topological groups. If G is a finite abelian group, then G and G^ are isomorphic, but not canonically. To make precise the statement that there is no canonical isomorphism between finite abelian groups and their dual groups (in general) requires thinking about dualizing not only on groups, but also on maps between the groups, in order to treat dualization as a functor
However, there is also a difference: V is isomorphic to its dual space V*, although not canonically so, while many groups G are not isomorphic to their dual groups (for instance, when G is T its dual is Z, and T is not isomorphic to Z as topological groups. If G is a finite abelian group, then G and G^ are isomorphic, but not canonically. To make precise the statement that there is no canonical isomorphism between finite abelian groups and their dual groups (in general) requires thinking about dualizing not only on groups, but also on maps between the groups, in order to treat dualization as a functor
and prove the identity functor and the dualization functor are not naturally equivalent.
A character on the infinite cyclic group of integers Z under addition is determined by its value at the generator 1. Thus for any character χ on Z, χ(n)=χ(1)n. Moreover, this formula defines a character for any choice of χ(1) in T. The topology of uniform convergence on compact sets is in this case the topology of pointwise convergence
. This is the topology of the circle group inherited from the complex numbers.
The dual of T is canonically isomorphic with Z. Proof: a character on T is of the form z → zn for n an integer. Since T is compact, the topology on the dual group is that of uniform convergence, which turns out to be the discrete topology.
The group of real numbers R, is isomorphic to its own dual; the characters on R are of the form r → e i θ r. With these dualities, the version of the Fourier transform to be introduced next coincides with the classical Fourier transform
on R.
Analogously, the p-adic numbers Qp are isomorphic to its dual. It follows that the adele
s are self-dual.
The various Fourier transforms can be classified in terms of their domain and transform domain (the group and dual group) as follows:
A group that is isomorphic (as topological groups) to its dual group is called self-dual. While the reals and Z/nZ are self-dual, the group and the dual group are not naturally isomorphic, and should be thought of as two different groups.
. If a function is in , then the Fourier transform is the function
, then the Fourier transform is the function 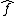 on
on  defined by
defined by

where the integral is relative to Haar measure
μ on G. This is also denoted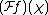 . Note the Fourier transform depends on the
. Note the Fourier transform depends on the
choice of Haar measure.
It is not too difficult to show that the Fourier transform of an L1 function on G is a bounded continuous function on G^ which vanishes at infinity. The Fourier inversion formula for L1-functions says that for each Haar measure μ on G there is a unique Haar measure on G^ such that whenever f is in L1(G) and its Fourier transform
on G^ such that whenever f is in L1(G) and its Fourier transform  is in L1(G^), we have
is in L1(G^), we have
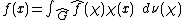
for μ-almost all x in G. If f is continuous then this identity holds for all x. (The inverse Fourier transform of an integrable function on G^ is given by
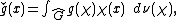
where the integral is relative to the Haar measure ν on the dual group G^.) The measure on G^ that appears in the Fourier inversion formula is called the dual measure to
on G^ that appears in the Fourier inversion formula is called the dual measure to 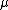 and may be denoted
and may be denoted 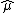 .
.
As an example, suppose G = Rn, so we can think about G^ as Rn by the pairing . If we use for
. If we use for 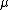 Lebesgue measure on Euclidean space, we obtain the ordinary Fourier transform
Lebesgue measure on Euclidean space, we obtain the ordinary Fourier transform
on Rn and the dual measure needed for the Fourier inversion formula is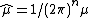 . If we want to get a Fourier inversion formula with the same measure on both sides (that is, since we can think about Rn as its own dual space we can ask for
. If we want to get a Fourier inversion formula with the same measure on both sides (that is, since we can think about Rn as its own dual space we can ask for  to equal
to equal 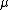 ) then we need to use
) then we need to use
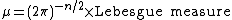

However, if we change the way we identify Rn with its dual group, by using the pairing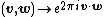 , then Lebesgue measure on Rn is equal to its own dual measure. This convention minimizes the number of factors of
, then Lebesgue measure on Rn is equal to its own dual measure. This convention minimizes the number of factors of 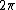 that show up in various places when computing Fourier transforms or inverse Fourier transforms on Euclidean space. (In effect it limits the
that show up in various places when computing Fourier transforms or inverse Fourier transforms on Euclidean space. (In effect it limits the 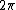 only to the exponent rather than as some messy factor outside the integral sign.) Note that the choice of how to identify Rn with its dual group affects the meaning of the term *self-dual function*, which is a function on Rn equal to its own Fourier transform: using the classical pairing
only to the exponent rather than as some messy factor outside the integral sign.) Note that the choice of how to identify Rn with its dual group affects the meaning of the term *self-dual function*, which is a function on Rn equal to its own Fourier transform: using the classical pairing 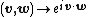 the function
the function 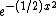 is self-dual, but using the (cleaner) pairing
is self-dual, but using the (cleaner) pairing 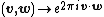 makes
makes 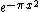 self-dual instead.
self-dual instead.
, where multiplication is convolution: if f, g are integrable functions then the convolution of f and g is defined as
Theorem The Banach space L1(G) is an associative and commutative algebra under convolution.
This algebra is referred to as the Group Algebra of G. By completeness of L1(G), it is a Banach algebra
. The Banach algebra L1(G) has a multiplicative identity element if and only if G is a discrete group. In general, however, it has an approximate identity
which is a net (or generalized sequence) indexed on a directed set I, {ei}i with the property that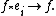
The Fourier transform takes convolution to multiplication, that is: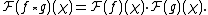
In particular, to every group character on G corresponds a unique multiplicative linear functional on the group algebra defined by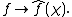
It is an important property of the group algebra that these exhaust the set of non-trivial (that is, not identically zero) multiplicative linear functionals on the group algebra. See section 34 of the Loomis reference.
Theorem. Choose a Haar measure μ on G and let ν be the dual measure on G^ as defined above. If f is a continuous complex-valued continuous function of compact support on G, its Fourier transform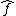 is in L2(G^) and
is in L2(G^) and
In particular, the Fourier transform is an L2 isometry from the complex-valued continuous functions of compact support on G to the L2-functions on G^ (using the L2-norm with respect to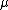 for functions on G and the L2-norm with respect to ν for functions on G^.
for functions on G and the L2-norm with respect to ν for functions on G^.
Since the complex-valued continuous functions of compact support on G are L2-dense, there is a unique extension of the Fourier transform from that space to a unitary operator
and we have the formula
for all f in L2(G).
Note that for non-compact locally compact groups G the space L1(G) does not contain L2(G), so the Fourier transform of general L2-functions on G is *not* given by any kind of integration formula (or really any explicit formula). To define the L2 Fourier transform one has to resort to some technical trick such as starting on a dense subspace like the continuous functions with compact support and then extend the isometry by continuity to the whole space. This unitary extension of the Fourier transform is what we mean by the Fourier transform on the space of square integrable functions.
The dual group also has an inverse Fourier transform in its own right; it can be characterized as the inverse (or adjoint, since it is unitary) of the L2 Fourier transform. This is the content of the L2 Fourier inversion formula which follows.
Theorem. The adjoint of the Fourier transform restricted to continuous functions of compact support is the inverse Fourier transform
where ν is the dual measure to μ.
In the case G = T, the dual group G^ is naturally isomorphic to the group of integers Z and the Fourier transform specializes to the computation of coefficients of Fourier series
of periodic functions.
If G is a finite group, we recover the discrete Fourier transform
. Note that this case is very easy to prove directly.
Theorem. A locally compact abelian group G is compact if and only if
the dual group G^ is discrete. Conversely,
G is discrete if and only if G^ is compact.
That G being compact implies G^ is discrete or that G being discrete implies that G^ is compact is an elementary consequence of the definition of the compact-open topology on G^ and does not need Pontryagin duality. One uses Pontryagin duality to prove the converses.
The Bohr compactification
is defined for any topological group G, regardless of whether G is locally compact or abelian. One use made of Pontryagin duality between compact abelian groups and discrete abelian groups is to characterize the Bohr compactification of an arbitrary abelian locally compact topological group. The Bohr compactification B(G) of G is H^, where H has the group structure G^, but given the discrete topology. Since the inclusion map
is continuous and a homomorphism, the dual morphism
is a morphism into a compact group which is easily shown to satisfy the requisite universal property
.
See also almost periodic function
.
. In what follows, LCA is the category of locally compact abelian groups and continuous group homomorphisms. The dual group construction of G^ is a contravariant functor LCA → LCA, represented (in the sense of representable functor
s) by the circle group T, as G^=Hom(G,T). In particular, the iterated functor G → (G^)^ is covariant.
Theorem. The dual group functor is an equivalence of categories
from LCA to LCAop.
Theorem. The iterated dual functor is naturally isomorphic
to the identity functor on LCA.
This isomorphism is analogous to the double dual of finite-dimensional vector spaces (a special case, for real and complex vector spaces).
The duality interchanges the subcategories of discrete groups and compact group
s. If R is a ring
and G is a left R-module
, the dual group G^ will become a right R-module; in this way we can also see that discrete left R-modules will be Pontryagin dual to compact right R-modules. The ring End(G) of endomorphism
s in LCA is changed by duality into its opposite ring (change the multiplication to the other order). For example if G is an infinite cyclic discrete group, G^ is a circle group: the former has End(G) = Z so this is true also of the latter.
in 1934. His treatment relied on the group being second-countable
and either compact or discrete. This was improved to cover the general locally compact abelian groups by Egbert van Kampen
in 1935 and André Weil
in 1940.
is called Tannaka-Krein duality
; but this diverges from the connection with harmonic analysis
, which needs to tackle the question of the Plancherel
measure on G^.
There are analogues of duality theory for noncommutative groups, some of which are formulated in the language of C*-algebras.
, which ignores the group structure, but recovers the topology.
Given a locally compact
Hausdorff
topological space
X, the space A = C0(X) of continuous complex-valued functions on X that vanish at infinity is a commutative C*-algebra, equipped with the uniform norm and pointwise addition, multiplication and complex conjugation. Conversely, the space of characters of this algebra, denoted ΦA, is naturally a topological space, and is identified with the space of functionals on C0(X) obtained by point evaluation. In particular, this identification gives rise to an isometric isomorphism C0(X)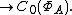 In the case where X = R is the real line, this is exactly the Fourier transform.
In the case where X = R is the real line, this is exactly the Fourier transform.
from G to its double-dual G^^ makes sense. If this mapping is an isomorphism, we say that G satisfies Pontryagin duality.
This has been extended in a number directions beyond the case that G is locally compact.
However, there is a fundamental aspect that changes if we want to consider Pontryagin duality beyond the locally compact case. In E. Martin-Peinador, A reflexible admissible topological group must be locally compact, Proc. Amer. Math. Soc. 123 (1995), 3563-3566, it is proved that if G is a Hausdorff abelian topological group that satisfies Pontryagin duality and the natural evaluation pairing from G x G^ to T, where (x,χ) goes to χ(x), is continuous, then G is locally compact. Thus any non-locally compact example of Pontryagin duality is a group where the natural evaluation pairing of G and G^ is not continuous.
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
and the theory of topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
s, Pontryagin duality explains the general properties of the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
on locally compact groups, such as R, the circle or finite cyclic groups.
Introduction
Pontryagin duality places in a unified context a number of observations about functions on the real line or on finite abelian groups:- Suitably regular complex-valued periodic functionPeriodic functionIn mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
s on the real line have Fourier seriesFourier seriesIn mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
and these functions can be recovered from their Fourier series;
- Suitably regular complex-valued functions on the real line have Fourier transforms that are also functions on the real line and, just as for periodic functions, these functions can be recovered from their Fourier transforms; and
- Complex-valued functions on a finite abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
have discrete Fourier transformDiscrete Fourier transformIn mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
s which are functions on the dual group, which is a (non-canonically) isomorphic group. Moreover any function on a finite group can be recovered from its discrete Fourier transform.
The theory, introduced by Lev Pontryagin and combined with Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
introduced by John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
, André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
and others depends on the theory of the dual group of a locally compact
Locally compact space
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
abelian group.
It is analogous to the dual vector space of a finite-dimensional vector space: a vector space V and its dual vector space V* are not naturally isomorphic, but their endomorphism algebras (matrix algebras) are: End(V)
 via the transpose. Similarly, a group G and its dual group
via the transpose. Similarly, a group G and its dual group 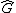 are not in general isomorphic, but their group algebra
are not in general isomorphic, but their group algebraGroup algebra
In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
s are: C(G)
 via the Fourier transform, though one must carefully define these algebras analytically. More categorically, this is not just an isomorphism of endomorphism algebras, but an isomorphism of categories – see categorical considerations.
via the Fourier transform, though one must carefully define these algebras analytically. More categorically, this is not just an isomorphism of endomorphism algebras, but an isomorphism of categories – see categorical considerations.Haar measure
A topological groupTopological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
is locally compact
Locally compact group
In mathematics, a locally compact group is a topological group G which is locally compact as a topological space. Locally compact groups are important because they have a natural measure called the Haar measure. This allows one to define integrals of functions on G.Many of the results of finite...
if and only if the identity e of the group has a compact neighborhood. This means that there is some open set V containing e whose closure is compact in the topology of G. One of the most remarkable facts about a locally compact group G is that it carries an essentially unique natural measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
, the Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
, which allows one to consistently measure the "size" of sufficiently regular subsets of G. "Sufficiently regular subset" here means a Borel set
Borel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
; that is, an element of the σ-algebra
Sigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
generated by the compact sets. More precisely, a right Haar measure on a locally compact group G is a countably additive measure μ defined on the Borel sets of G which is right invariant in the sense that μ(A x) = μ(A) for x an element of G and A a Borel subset of G and also satisfies some regularity conditions (spelled out in detail in the article on Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
). Except for positive scaling factors, a Haar measure on G is unique.
The Haar measure on G allows us to define the notion of integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
for (complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
-valued) Borel functions defined on the group. In particular, one may consider various Lp spaces associated to the Haar measure. Specifically,
Note that, since any two Haar measures on G are equal up to a scaling factor, this Lp-space is independent of the choice
of Haar measure and thus perhaps could be written as Lp(G). However, the Lp-norm on this space
depends on the choice of Haar measure, so if one wants to talk about isometries it is important to keep track of the Haar measure being used.
Examples of locally compact abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
groups are:
- Rn, for n a positive integer, with vector addition as group operation.
- The positive real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s with multiplication as operation. This group is isomorphic to R, by the exponential map.
- Any finite abelian group, with the discrete topology. By the structure theorem for finite abelian groups, all such groups are products of cyclic groups.
- The integers Z under addition, again with the discrete topology.
- The circle group, denoted T, for torusTorusIn geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
. This is the group of complex numbers of modulusAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
1. T is isomorphic as a topological group to the quotient groupQuotient groupIn mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
R/Z .
- The field Qp of p-adic numberP-adic numberIn mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
s under addition, with the usual p-adic topology.
The dual group
If G is a locally compact abelian group, a characterCharacter (mathematics)
In mathematics, a character is a special kind of function from a group to a field . There are at least two distinct, but overlapping meanings...
of G is a continuous group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
from G with values in the circle group T. The set of all characters on G can be made into a locally compact abelian group, called the dual group of G and denoted Ĝ. The group operation on the dual group is given by pointwise multiplication of characters, the inverse of a character is its complex conjugate and the topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
on the space of characters is that of uniform convergence on compact sets (i.e., the compact-open topology
Compact-open topology
In mathematics, the compact-open topology is a topology defined on the set of continuous maps between two topological spaces. The compact-open topology is one of the commonly-used topologies on function spaces, and is applied in homotopy theory and functional analysis...
, viewing Ĝ as a subset of the space of all continuous functions from G to T.). This topology in general is not metrizable. However, if the group G is a separable locally compact abelian group, then the dual group is metrizable.
This is analogous to the dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
in linear algebra: just as for a vector space V over a field K, the dual space is

so too is the dual group
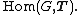 More abstractly, these are both examples of representable functor
More abstractly, these are both examples of representable functorRepresentable functor
In mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
s, being represented respectively by K and T.
The Pontryagin's duality theorem
Theorem The dual of G^ is canonically isomorphic to G, that is (G^)^ = G in a canonical way.Canonical
Canonical
Canonical is an adjective derived from canon. Canon comes from the greek word κανών kanon, "rule" or "measuring stick" , and is used in various meanings....
means that there is a naturally defined map from G into (G^)^; more importantly, the map should be functorial. The canonical isomorphism is defined as follows:
In other words, each group element x is identified to the evaluation character on the dual. This is exactly the same as the canonical isomorphism between a finite-dimensional vector space and its double dual,
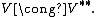 However, there is also a difference: V is isomorphic to its dual space V*, although not canonically so, while many groups G are not isomorphic to their dual groups (for instance, when G is T its dual is Z, and T is not isomorphic to Z as topological groups. If G is a finite abelian group, then G and G^ are isomorphic, but not canonically. To make precise the statement that there is no canonical isomorphism between finite abelian groups and their dual groups (in general) requires thinking about dualizing not only on groups, but also on maps between the groups, in order to treat dualization as a functor
However, there is also a difference: V is isomorphic to its dual space V*, although not canonically so, while many groups G are not isomorphic to their dual groups (for instance, when G is T its dual is Z, and T is not isomorphic to Z as topological groups. If G is a finite abelian group, then G and G^ are isomorphic, but not canonically. To make precise the statement that there is no canonical isomorphism between finite abelian groups and their dual groups (in general) requires thinking about dualizing not only on groups, but also on maps between the groups, in order to treat dualization as a functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
and prove the identity functor and the dualization functor are not naturally equivalent.
Examples
The dual of Z is isomorphic to the circle group T. Proof:A character on the infinite cyclic group of integers Z under addition is determined by its value at the generator 1. Thus for any character χ on Z, χ(n)=χ(1)n. Moreover, this formula defines a character for any choice of χ(1) in T. The topology of uniform convergence on compact sets is in this case the topology of pointwise convergence
Pointwise convergence
In mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
. This is the topology of the circle group inherited from the complex numbers.
The dual of T is canonically isomorphic with Z. Proof: a character on T is of the form z → zn for n an integer. Since T is compact, the topology on the dual group is that of uniform convergence, which turns out to be the discrete topology.
The group of real numbers R, is isomorphic to its own dual; the characters on R are of the form r → e i θ r. With these dualities, the version of the Fourier transform to be introduced next coincides with the classical Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
on R.
Analogously, the p-adic numbers Qp are isomorphic to its dual. It follows that the adele
Adele ring
In algebraic number theory and topological algebra, the adele ring is a topological ring which is built on the field of rational numbers . It involves all the completions of the field....
s are self-dual.
The various Fourier transforms can be classified in terms of their domain and transform domain (the group and dual group) as follows:
| Transform | Original domain | Transform domain |
|---|---|---|
| Fourier transform | R | R |
| Fourier series Fourier series In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines... |
T | Z |
| Discrete-time Fourier transform Discrete-time Fourier transform In mathematics, the discrete-time Fourier transform is one of the specific forms of Fourier analysis. As such, it transforms one function into another, which is called the frequency domain representation, or simply the "DTFT", of the original function . But the DTFT requires an input function... (DTFT) |
Z | T |
| Discrete Fourier transform Discrete Fourier transform In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function... (DFT) |
Z/nZ | Z/nZ |
A group that is isomorphic (as topological groups) to its dual group is called self-dual. While the reals and Z/nZ are self-dual, the group and the dual group are not naturally isomorphic, and should be thought of as two different groups.
Fourier transform and Fourier inversion formula for L1-functions
The dual group of a locally compact abelian group is used as the underlying space for an abstract version of the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
. If a function is in
 , then the Fourier transform is the function
, then the Fourier transform is the function 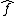 on
on  defined by
defined by
where the integral is relative to Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
μ on G. This is also denoted
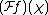 . Note the Fourier transform depends on the
. Note the Fourier transform depends on thechoice of Haar measure.
It is not too difficult to show that the Fourier transform of an L1 function on G is a bounded continuous function on G^ which vanishes at infinity. The Fourier inversion formula for L1-functions says that for each Haar measure μ on G there is a unique Haar measure
 on G^ such that whenever f is in L1(G) and its Fourier transform
on G^ such that whenever f is in L1(G) and its Fourier transform  is in L1(G^), we have
is in L1(G^), we have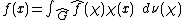
for μ-almost all x in G. If f is continuous then this identity holds for all x. (The inverse Fourier transform of an integrable function on G^ is given by
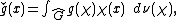
where the integral is relative to the Haar measure ν on the dual group G^.) The measure
 on G^ that appears in the Fourier inversion formula is called the dual measure to
on G^ that appears in the Fourier inversion formula is called the dual measure to 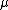 and may be denoted
and may be denoted 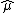 .
.As an example, suppose G = Rn, so we can think about G^ as Rn by the pairing
 . If we use for
. If we use for 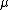 Lebesgue measure on Euclidean space, we obtain the ordinary Fourier transform
Lebesgue measure on Euclidean space, we obtain the ordinary Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
on Rn and the dual measure needed for the Fourier inversion formula is
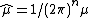 . If we want to get a Fourier inversion formula with the same measure on both sides (that is, since we can think about Rn as its own dual space we can ask for
. If we want to get a Fourier inversion formula with the same measure on both sides (that is, since we can think about Rn as its own dual space we can ask for  to equal
to equal 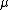 ) then we need to use
) then we need to use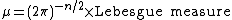

However, if we change the way we identify Rn with its dual group, by using the pairing
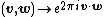 , then Lebesgue measure on Rn is equal to its own dual measure. This convention minimizes the number of factors of
, then Lebesgue measure on Rn is equal to its own dual measure. This convention minimizes the number of factors of 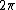 that show up in various places when computing Fourier transforms or inverse Fourier transforms on Euclidean space. (In effect it limits the
that show up in various places when computing Fourier transforms or inverse Fourier transforms on Euclidean space. (In effect it limits the 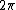 only to the exponent rather than as some messy factor outside the integral sign.) Note that the choice of how to identify Rn with its dual group affects the meaning of the term *self-dual function*, which is a function on Rn equal to its own Fourier transform: using the classical pairing
only to the exponent rather than as some messy factor outside the integral sign.) Note that the choice of how to identify Rn with its dual group affects the meaning of the term *self-dual function*, which is a function on Rn equal to its own Fourier transform: using the classical pairing 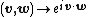 the function
the function 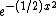 is self-dual, but using the (cleaner) pairing
is self-dual, but using the (cleaner) pairing 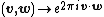 makes
makes 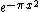 self-dual instead.
self-dual instead.The group algebra
The space of integrable functions on a locally compact abelian group G is an algebraAlgebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, where multiplication is convolution: if f, g are integrable functions then the convolution of f and g is defined as

Theorem The Banach space L1(G) is an associative and commutative algebra under convolution.
This algebra is referred to as the Group Algebra of G. By completeness of L1(G), it is a Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
. The Banach algebra L1(G) has a multiplicative identity element if and only if G is a discrete group. In general, however, it has an approximate identity
Approximate identity
In functional analysis and ring theory, an approximate identity is a net in a Banach algebra or ring that acts as a substitute for an identity element....
which is a net (or generalized sequence) indexed on a directed set I, {ei}i with the property that
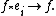
The Fourier transform takes convolution to multiplication, that is:
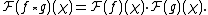
In particular, to every group character on G corresponds a unique multiplicative linear functional on the group algebra defined by
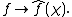
It is an important property of the group algebra that these exhaust the set of non-trivial (that is, not identically zero) multiplicative linear functionals on the group algebra. See section 34 of the Loomis reference.
Plancherel and L2 Fourier inversion theorems
As we have stated, the dual group of a locally compact abelian group is a locally compact abelian group in its own right and thus has a Haar measure, or more precisely a whole family of scale-related Haar measures.Theorem. Choose a Haar measure μ on G and let ν be the dual measure on G^ as defined above. If f is a continuous complex-valued continuous function of compact support on G, its Fourier transform
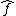 is in L2(G^) and
is in L2(G^) andIn particular, the Fourier transform is an L2 isometry from the complex-valued continuous functions of compact support on G to the L2-functions on G^ (using the L2-norm with respect to
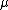 for functions on G and the L2-norm with respect to ν for functions on G^.
for functions on G and the L2-norm with respect to ν for functions on G^.Since the complex-valued continuous functions of compact support on G are L2-dense, there is a unique extension of the Fourier transform from that space to a unitary operator
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
and we have the formula
for all f in L2(G).
Note that for non-compact locally compact groups G the space L1(G) does not contain L2(G), so the Fourier transform of general L2-functions on G is *not* given by any kind of integration formula (or really any explicit formula). To define the L2 Fourier transform one has to resort to some technical trick such as starting on a dense subspace like the continuous functions with compact support and then extend the isometry by continuity to the whole space. This unitary extension of the Fourier transform is what we mean by the Fourier transform on the space of square integrable functions.
The dual group also has an inverse Fourier transform in its own right; it can be characterized as the inverse (or adjoint, since it is unitary) of the L2 Fourier transform. This is the content of the L2 Fourier inversion formula which follows.
Theorem. The adjoint of the Fourier transform restricted to continuous functions of compact support is the inverse Fourier transform
where ν is the dual measure to μ.
In the case G = T, the dual group G^ is naturally isomorphic to the group of integers Z and the Fourier transform specializes to the computation of coefficients of Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
of periodic functions.
If G is a finite group, we recover the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
. Note that this case is very easy to prove directly.
Bohr compactification and almost-periodicity
One important application of Pontryagin duality is the following characterization of compact abelian topological groups:Theorem. A locally compact abelian group G is compact if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the dual group G^ is discrete. Conversely,
G is discrete if and only if G^ is compact.
That G being compact implies G^ is discrete or that G being discrete implies that G^ is compact is an elementary consequence of the definition of the compact-open topology on G^ and does not need Pontryagin duality. One uses Pontryagin duality to prove the converses.
The Bohr compactification
Bohr compactification
In mathematics, the Bohr compactification of a topological group G is a compact Hausdorff topological group H that may be canonically associated to G. Its importance lies in the reduction of the theory of uniformly almost periodic functions on G to the theory of continuous functions on H...
is defined for any topological group G, regardless of whether G is locally compact or abelian. One use made of Pontryagin duality between compact abelian groups and discrete abelian groups is to characterize the Bohr compactification of an arbitrary abelian locally compact topological group. The Bohr compactification B(G) of G is H^, where H has the group structure G^, but given the discrete topology. Since the inclusion map
Inclusion map
In mathematics, if A is a subset of B, then the inclusion map is the function i that sends each element, x of A to x, treated as an element of B:i: A\rightarrow B, \qquad i=x....
is continuous and a homomorphism, the dual morphism
is a morphism into a compact group which is easily shown to satisfy the requisite universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
.
See also almost periodic function
Almost periodic function
In mathematics, an almost periodic function is, loosely speaking, a function of a real number that is periodic to within any desired level of accuracy, given suitably long, well-distributed "almost-periods". The concept was first studied by Harald Bohr and later generalized by Vyacheslav Stepanov,...
.
Categorical considerations
It is useful to regard the dual group functoriallyFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
. In what follows, LCA is the category of locally compact abelian groups and continuous group homomorphisms. The dual group construction of G^ is a contravariant functor LCA → LCA, represented (in the sense of representable functor
Representable functor
In mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
s) by the circle group T, as G^=Hom(G,T). In particular, the iterated functor G → (G^)^ is covariant.
Theorem. The dual group functor is an equivalence of categories
Equivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
from LCA to LCAop.
Theorem. The iterated dual functor is naturally isomorphic
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
to the identity functor on LCA.
This isomorphism is analogous to the double dual of finite-dimensional vector spaces (a special case, for real and complex vector spaces).
The duality interchanges the subcategories of discrete groups and compact group
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
s. If R is a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
and G is a left R-module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, the dual group G^ will become a right R-module; in this way we can also see that discrete left R-modules will be Pontryagin dual to compact right R-modules. The ring End(G) of endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
s in LCA is changed by duality into its opposite ring (change the multiplication to the other order). For example if G is an infinite cyclic discrete group, G^ is a circle group: the former has End(G) = Z so this is true also of the latter.
History
The foundations for the theory of locally compact abelian groups and their duality were laid down by Lev Semenovich PontryaginLev Semenovich Pontryagin
Lev Semenovich Pontryagin was a Soviet mathematician. He was born in Moscow and lost his eyesight due to a primus stove explosion when he was 14...
in 1934. His treatment relied on the group being second-countable
Second-countable space
In topology, a second-countable space, also called a completely separable space, is a topological space satisfying the second axiom of countability. A space is said to be second-countable if its topology has a countable base...
and either compact or discrete. This was improved to cover the general locally compact abelian groups by Egbert van Kampen
Egbert van Kampen
Egbert Rudolf van Kampen was a mathematician. He made important contributions to topology, especially to the study of fundamental groups....
in 1935 and André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
in 1940.
Non-commutative theory
Such a theory cannot exist in the same form for non-commutative groups G, since in that case the appropriate dual object G^ of isomorphism classes of representations cannot only contain one-dimensional representations, and will fail to be a group. The generalisation that has been found useful in category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
is called Tannaka-Krein duality
Tannaka-Krein duality
In mathematics, Tannaka–Krein duality theory concerns the interaction of a compact topological group and its category of linear representations. Its natural extension to the non-Abelian case is the Grothendieck duality theory....
; but this diverges from the connection with harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
, which needs to tackle the question of the Plancherel
Michel Plancherel
Michel Plancherel was a Swiss mathematician. He was born in Bussy and obtained his diploma in mathematics from the University of Fribourg in 1907...
measure on G^.
There are analogues of duality theory for noncommutative groups, some of which are formulated in the language of C*-algebras.
Locally compact Hausdorff space
A further generalization is given by the Gelfand representationGelfand representation
In mathematics, the Gelfand representation in functional analysis has two related meanings:* a way of representing commutative Banach algebras as algebras of continuous functions;...
, which ignores the group structure, but recovers the topology.
Given a locally compact
Locally compact space
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X, the space A = C0(X) of continuous complex-valued functions on X that vanish at infinity is a commutative C*-algebra, equipped with the uniform norm and pointwise addition, multiplication and complex conjugation. Conversely, the space of characters of this algebra, denoted ΦA, is naturally a topological space, and is identified with the space of functionals on C0(X) obtained by point evaluation. In particular, this identification gives rise to an isometric isomorphism C0(X)
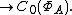 In the case where X = R is the real line, this is exactly the Fourier transform.
In the case where X = R is the real line, this is exactly the Fourier transform.Others
When G is a Hausdorff abelian topological group, the group G^ with the compact-open topology is a Hausdorff abelian topological group and the natural mappingfrom G to its double-dual G^^ makes sense. If this mapping is an isomorphism, we say that G satisfies Pontryagin duality.
This has been extended in a number directions beyond the case that G is locally compact.
- S.Kaplan, in "Extensions of the Pontryagin duality" ("part I: infinite products", Duke Math. J. 15 (1948) 649–658, and "part II: direct and inverse limits", same journal, 17 (1950), 419–435) showed that arbitrary products and countable inverse limits of locally compact (Hausdorff) abelian groups satisfy Pontryagin duality. Note that an infinite product of locally compact non-compact spaces is not locally compact.
- Later, in 1975, R.Venkataraman ("Extensions of Pontryagin Duality", Math. Z. 143, 105-112) showed, among other facts, that every open subgroup of an abelian topological group which satisfies Pontryagin duality itself satisfies Pontryagin duality.
- More recently, S. Ardanza-Trevijano and M.J. Chasco have extended the results of Kaplan mentioned above. They showed, in "The Pontryagin duality of sequential limits of topological Abelian groups", Journal of Pure and Applied Algebra 202 (2005), 11–21, that direct and inverse limits of sequences of abelian groups satisfying Pontryagin duality also satisfy Pontryagin duality if the groups are metrizable or kω-spaces but not necessarily locally compact, provided some extra conditions are satisfied by the sequences.
However, there is a fundamental aspect that changes if we want to consider Pontryagin duality beyond the locally compact case. In E. Martin-Peinador, A reflexible admissible topological group must be locally compact, Proc. Amer. Math. Soc. 123 (1995), 3563-3566, it is proved that if G is a Hausdorff abelian topological group that satisfies Pontryagin duality and the natural evaluation pairing from G x G^ to T, where (x,χ) goes to χ(x), is continuous, then G is locally compact. Thus any non-locally compact example of Pontryagin duality is a group where the natural evaluation pairing of G and G^ is not continuous.