
Algebraic number
Encyclopedia
In mathematics
, an algebraic number is a number that is a root of a non-zero polynomial
in one variable with rational
(or equivalently, integer
) coefficients. Numbers such as π
that are not algebraic are said to be transcendental
; almost all
real numbers are transcendental. (Here "almost all" has the sense "all but a set of Lebesgue measure
zero"; see Properties below.)
, sometimes denoted by A (which may also denote the adele ring
) or Q. Every root of a polynomial equation whose coefficients are algebraic numbers is again algebraic. This can be rephrased by saying that the field of algebraic numbers is algebraically closed
. In fact, it is the smallest algebraically closed field containing the rationals, and is therefore called the algebraic closure
of the rationals.
s, subtraction
s, multiplication
s, division
s, and taking nth roots (where n is a positive integer) are algebraic. The converse, however, is not true: there are algebraic numbers which cannot be obtained in this manner. All of these numbers are solutions to polynomials of degree ≥ 5. This is a result of Galois theory
(see Quintic equation
s and the Abel–Ruffini theorem
). An example of such a number is the unique real root of polynomial (which is approximately 1.167304).
is an algebraic number which is a root of a polynomial with integer coefficients with leading coefficient 1 (a monic polynomial). Examples of algebraic integers are , , and (Note, therefore, that the algebraic integers constitute a proper superset
of the integer
s, as the latter are the roots of monic polynomials for all
The sum, difference and product of algebraic integers are again algebraic integers, which means that the algebraic integers form a ring. The name algebraic integer comes from the fact that the only rational numbers which are algebraic integers are the integers, and because the algebraic integers in any number field
are in many ways analogous to the integers. If K is a number field, its ring of integers
is the subring of algebraic integers in K, and is frequently denoted as OK.
These are the prototypical examples of Dedekind domain
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an algebraic number is a number that is a root of a non-zero polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
in one variable with rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
(or equivalently, integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
) coefficients. Numbers such as π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
that are not algebraic are said to be transcendental
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
; almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
real numbers are transcendental. (Here "almost all" has the sense "all but a set of Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
zero"; see Properties below.)
Examples
- The rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, expressed as the quotient of two integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s a and b, b not equal to zero, satisfy the above definition because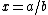 is the root of
is the root of 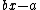 .
.
- The constructible numberConstructible numberA point in the Euclidean plane is a constructible point if, given a fixed coordinate system , the point can be constructed with unruled straightedge and compass...
s (those that, starting with a unit, can be constructed with straightedge and compass, e.g. the square root of 2).
- The quadratic surds (roots of a quadratic polynomial
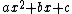 with integer coefficients
with integer coefficients  ,
,  , and
, and  ) are algebraic numbers. If the quadratic polynomial is monic
) are algebraic numbers. If the quadratic polynomial is monic  then the roots are quadratic integerQuadratic integerIn number theory, quadratic integers are a generalization of the rational integers to quadratic fields. Important examples include the Gaussian integers and the Eisenstein integers. Though they have been studied for more than a hundred years, many open problems remain.- Definition :Quadratic...
then the roots are quadratic integerQuadratic integerIn number theory, quadratic integers are a generalization of the rational integers to quadratic fields. Important examples include the Gaussian integers and the Eisenstein integers. Though they have been studied for more than a hundred years, many open problems remain.- Definition :Quadratic...
s.
- Gaussian integerGaussian integerIn number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
s: those complex numbers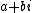 where both
where both  and
and  are integers are also quadratic integers.
are integers are also quadratic integers.
- Trigonometric functions of rationalRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
multiples of (except when undefined). For example, each of cos(
(except when undefined). For example, each of cos(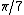 ), cos(
), cos( ), cos(
), cos(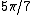 ) satisfies
) satisfies 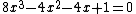 . This polynomial is irreducibleIrreducible polynomialIn mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
. This polynomial is irreducibleIrreducible polynomialIn mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
over the rationals, and so these three cosines are conjugate algebraic numbers. Likewise, tan(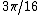 ), tan(
), tan( ), tan(
), tan( ), tan(
), tan(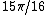 ) all satisfy the irreducible polynomial
) all satisfy the irreducible polynomial  , and so are conjugate algebraic integers.
, and so are conjugate algebraic integers.
- Some irrational numberIrrational numberIn mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s are algebraic and some are not:- The numbers
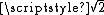 and
and  are algebraic since they are the roots of polynomials
are algebraic since they are the roots of polynomials 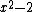 and
and 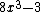 , respectively.
, respectively. - The golden ratioGolden ratioIn mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
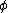 is algebraic since it is a root of the polynomial
is algebraic since it is a root of the polynomial 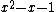 .
. - The numbers
 Pi' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
Pi' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
and E (mathematical constant)The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
E (mathematical constant)The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
are not algebraic numbers (see the Lindemann–Weierstrass theoremLindemann–Weierstrass theoremIn mathematics, the Lindemann–Weierstrass theorem is a result that is very useful in establishing the transcendence of numbers. It states that if 1, ..., are algebraic numbers which are linearly independent over the rational numbers ', then 1, ..., are algebraically...
); hence they are transcendental.
- The numbers
Properties
- The set of algebraic numbers is countableCountable setIn mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
(enumerable). - Hence, the set of algebraic numbers has Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
zero (as a subset of the complex numbers), i.e. "almost allAlmost everywhereIn measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
" complex numbers are not algebraic. - Given an algebraic number, there is a unique monic polynomial (with rational coefficients) of least degreeDegree of a polynomialThe degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
that has the number as a root. This polynomial is called its minimal polynomialMinimal polynomial (field theory)In field theory, given a field extension E / F and an element α of E that is an algebraic element over F, the minimal polynomial of α is the monic polynomial p, with coefficients in F, of least degree such that p = 0...
. If its minimal polynomial has degree , then the algebraic number is said to be of degree
, then the algebraic number is said to be of degree  . An algebraic number of degree 1 is a rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
. An algebraic number of degree 1 is a rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
. - All algebraic numbers are computableComputable numberIn mathematics, particularly theoretical computer science and mathematical logic, the computable numbers, also known as the recursive numbers or the computable reals, are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm...
and therefore definableDefinable numberA real number a is first-order definable in the language of set theory, without parameters, if there is a formula φ in the language of set theory, with one free variable, such that a is the unique real number such that φ holds in the standard model of set theory .For the purposes of this article,...
.
The field of algebraic numbers
The sum, difference, product and quotient of two algebraic numbers is again algebraic (this fact can be demonstrated using the resultant), and the algebraic numbers therefore form a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, sometimes denoted by A (which may also denote the adele ring
Adele ring
In algebraic number theory and topological algebra, the adele ring is a topological ring which is built on the field of rational numbers . It involves all the completions of the field....
) or Q. Every root of a polynomial equation whose coefficients are algebraic numbers is again algebraic. This can be rephrased by saying that the field of algebraic numbers is algebraically closed
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
. In fact, it is the smallest algebraically closed field containing the rationals, and is therefore called the algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of the rationals.
Numbers defined by radicals
All numbers which can be obtained from the integers using a finite number of integer additionAddition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
s, subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
s, multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
s, division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
s, and taking nth roots (where n is a positive integer) are algebraic. The converse, however, is not true: there are algebraic numbers which cannot be obtained in this manner. All of these numbers are solutions to polynomials of degree ≥ 5. This is a result of Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
(see Quintic equation
Quintic equation
In mathematics, a quintic function is a function of the formg=ax^5+bx^4+cx^3+dx^2+ex+f,\,where a, b, c, d, e and f are members of a field, typically the rational numbers, the real numbers or the complex numbers, and a is nonzero...
s and the Abel–Ruffini theorem
Abel–Ruffini theorem
In algebra, the Abel–Ruffini theorem states that there is no general algebraic solution—that is, solution in radicals— to polynomial equations of degree five or higher.- Interpretation :...
). An example of such a number is the unique real root of polynomial (which is approximately 1.167304).
Closed-form number
Algebraic numbers are all numbers that can be defined explicitly or implicitly in terms of polynomials, starting from the rational numbers. One may generalize this to "closed-form numbers", which may be defined in various ways. Most broadly, any number that can be defined explicitly or implicitly in terms of polynomials, exponentials, and logarithms – these are called "elementary numbers", and include the algebraic numbers, plus some transcendental numbers. Most narrowly, one may consider numbers explicitly defined in terms of polynomials, exponentials, and logarithms – this does not include algebraic numbers, but does include some simple transcendental numbers such as e or log(2).Algebraic integers
An algebraic integerAlgebraic integer
In number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...
is an algebraic number which is a root of a polynomial with integer coefficients with leading coefficient 1 (a monic polynomial). Examples of algebraic integers are , , and (Note, therefore, that the algebraic integers constitute a proper superset
SuperSet
SuperSet Software was a group founded by friends and former Eyring Research Institute co-workers Drew Major, Dale Neibaur, Kyle Powell and later joined by Mark Hurst...
of the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, as the latter are the roots of monic polynomials for all
The sum, difference and product of algebraic integers are again algebraic integers, which means that the algebraic integers form a ring. The name algebraic integer comes from the fact that the only rational numbers which are algebraic integers are the integers, and because the algebraic integers in any number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
are in many ways analogous to the integers. If K is a number field, its ring of integers
Ring of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
is the subring of algebraic integers in K, and is frequently denoted as OK.
These are the prototypical examples of Dedekind domain
Dedekind domain
In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
s.
Special classes of algebraic number
- Gaussian integerGaussian integerIn number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
- Eisenstein integerEisenstein integerIn mathematics, Eisenstein integers , also known as Eulerian integers , are complex numbers of the formz = a + b\omega \,\!where a and b are integers and...
- Quadratic irrationalQuadratic irrationalIn mathematics, a quadratic irrational is an irrational number that is the solution to some quadratic equation with rational coefficients...
- Fundamental unitFundamental unit (number theory)In algebraic number theory, a fundamental unit is a generator for the torsion-free unit group of the ring of integers of a number field, when that group is infinite cyclic...
- Root of unityRoot of unityIn mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
- Gaussian periodGaussian periodIn mathematics, in the area of number theory, a Gaussian period is a certain kind of sum of roots of unity. The periods permit explicit calculations in cyclotomic fields connected with Galois theory and with harmonic analysis . They are basic in the classical theory called cyclotomy...
- Pisot-Vijayaraghavan numberPisot-Vijayaraghavan numberIn mathematics, a Pisot–Vijayaraghavan number, also called simply a Pisot number or a PV number, is a real algebraic integer greater than 1 such that all its Galois conjugates are less than 1 in absolute value. These numbers were discovered by Axel Thue in 1912 and rediscovered by G. H. Hardy in...
- Salem number

