Vector spaces without fields
Encyclopedia
In mathematics, the conventional definition of the concept of vector space
relies upon the algebra
ic concept of a field
. This article treats an algebraic definition that does not require that concept. If vector spaces are redefined as (universal) algebras
as below, no preliminary introduction of fields is necessary. On the contrary, fields will come from such vector space algebras.
One of the ways to do this is to keep the first four Abelian group
axioms on addition in the standard formal definition
and to formalize its geometric idea of scaling only by notions that concern every universal algebra. Vector space algebras consist of one binary operation + and of "unary" operations δ, which form a nonempty set Δ, that satisfy the following conditions, which do not involve fields.
Ricci (2008) proves that these vector space algebras are the very universal algebras that any standard vector space defines by its addition and the scalar multiplications by any given scalar (namely each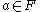
gets a 
such that 
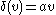). Ricci (2007) proves that every such a universal algebra defines a suitable field. (Hence, it proves that these conditions imply all the axioms of the standard formal definition
, as well as all the defining properties in definition 3 of a field
.)
Since the field is defined from such vector space algebra, this is an algebraic construction of fields, which is an instance of a more general algebraic construction: the "endowed dilatation monoid" (Ricci 2007). However, as far as fields are concerned, there also is a geometric construction. Chapter II in (Artin 1957) shows how to get them starting from geometric axioms concerning points and lines.
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
relies upon the algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
ic concept of a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. This article treats an algebraic definition that does not require that concept. If vector spaces are redefined as (universal) algebras
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
as below, no preliminary introduction of fields is necessary. On the contrary, fields will come from such vector space algebras.
One of the ways to do this is to keep the first four Abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
axioms on addition in the standard formal definition
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
and to formalize its geometric idea of scaling only by notions that concern every universal algebra. Vector space algebras consist of one binary operation + and of "unary" operations δ, which form a nonempty set Δ, that satisfy the following conditions, which do not involve fields.
- (Total homogeneous algebra) There is a single set V such that every operation takes its two arguments or its argument from the whole V and gives its value in it.
- (Abelian group) + satisfies the above mentioned axioms.
- (Basis dilation) There is a basis setBasis (Universal Algebra)In universal algebra a basis is a structure inside of some algebras, which are called free algebras. It generates all algebra elements from its own elements by the algebra operations in an independent manner...
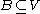such that, for every such δ that is not constant, all the values 
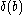, where b ranges over B, again form a basis set. - (Dilatations) Δ is the set of all and only functions that satisfy the previous conditions and preserve all operations, namely
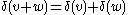and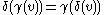 
, for all 
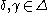and all 
.
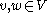Ricci (2008) proves that these vector space algebras are the very universal algebras that any standard vector space defines by its addition and the scalar multiplications by any given scalar (namely each
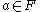gets a such that 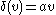). Ricci (2007) proves that every such a universal algebra defines a suitable field. (Hence, it proves that these conditions imply all the axioms of the standard formal definitionVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, as well as all the defining properties in definition 3 of a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
.)
Since the field is defined from such vector space algebra, this is an algebraic construction of fields, which is an instance of a more general algebraic construction: the "endowed dilatation monoid" (Ricci 2007). However, as far as fields are concerned, there also is a geometric construction. Chapter II in (Artin 1957) shows how to get them starting from geometric axioms concerning points and lines.