
Closure (topology)
Encyclopedia
In mathematics
, the closure of a subset S in a topological space
consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure
of S. The notion of closure is in many ways dual
to the notion of interior
.
, x is a point of closure of S if every open ball centered at x contains a point of S (this point may be x itself).
This definition generalises to any subset S of a metric space
X. Fully expressed, for X a metric space with metric d, x is a point of closure of S if for every r > 0, there is a y in S such that the distance d(x, y) < r. (Again, we may have x = y.) Another way to express this is to say that x is a point of closure of S if the distance d(x, S) := inf
{d(x, s) : s in S} = 0.
This definition generalises to topological space
s by replacing "open ball" or "ball" with "neighbourhood". Let S be a subset of a topological space X. Then x is a point of closure of S if every neighbourhood of x contains a point of S. Note that this definition does not depend upon whether neighbourhoods are required to be open.
. The difference between the two definitions is subtle but important — namely, in the definition of limit point, every neighborhood of the point x in question must contain a point of the set other than x itself.
Thus, every limit point is a point of closure, but not every point of closure is a limit point. A point of closure which is not a limit point is an isolated point
. In other words, a point x is an isolated point of S if it is an element of S and if there is a neighbourhood of x which contains no other points of S other than x itself.
For a given set S and point x, x is a point of closure of S if and only if x is an element of S or x is a limit point of S (or both).
 or
or  . The closure of a set has the following properties.
. The closure of a set has the following properties.
Sometimes the second or third property above is taken as the definition of the topological closure, which still make sense when applied to other types of closures (see below).
In a first-countable space
(such as a metric space
), cl(S) is the set of all limits
of all convergent sequence
s of points in S. For a general topological space, this statement remains true if one replaces "sequence" by "net
" or "filter
".
Note that these properties are also satisfied if "closure", "superset", "intersection", "contains/containing", "smallest" and "closed" are replaced by "interior", "subset", "union", "contained in", "largest", and "open". For more on this matter, see closure operator below.
On the set of real numbers one can put other topologies rather than the standard one.
These examples show that the closure of a set depends upon the topology of the underlying space. The last two examples are special cases of the following.
The closure of a set also depends upon in which space we are taking the closure. For example, if X is the set of rational numbers, with the usual subspace topology
induced by the Euclidean space R, and if S = {q in Q : q2 > 2}, then S is closed in Q, and the closure of S in Q is S; however, the closure of S in the Euclidean space R is the set of all real numbers greater than or equal to
to the interior
operator o, in the sense that
and also
where X denotes the topological space
containing S, and the backslash refers to the set-theoretic difference
.
Therefore, the abstract theory of closure operators and the Kuratowski closure axioms
can be easily translated into the language of interior operators, by replacing sets with their complements
.
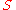 is closed
is closed
if and only if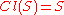 . In particular, the closure of the empty set
. In particular, the closure of the empty set
is the empty set, and the closure of itself is
itself is  . The closure of an intersection
. The closure of an intersection
of sets is always a subset
of (but need not be equal to) the intersection of the closures of the sets. In a union
of finitely many sets, the closure of the union and the union of the closures are equal; the union of zero sets is the empty set, and so this statement contains the earlier statement about the closure of the empty set as a special case. The closure of the union of infinitely many sets need not equal the union of the closures, but it is always a superset
of the union of the closures.
If is a subspace of
is a subspace of  containing
containing  , then the closure of
, then the closure of 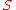 computed in
computed in  is equal to the intersection of
is equal to the intersection of  and the closure of
and the closure of  computed in
computed in  :
: 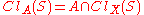 . In particular,
. In particular,  is dense in
is dense in  if and only if
if and only if
 is a subset of
is a subset of 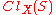 .
.
The powerset of a set X may be realized as a partial order category
P in which the objects are subsets and the morphisms are inclusions whenever A is a subset of B. Furthermore, a topology T on X is a subcategory of P with inclusion functor
whenever A is a subset of B. Furthermore, a topology T on X is a subcategory of P with inclusion functor  . The set of closed subsets containing a fixed subset
. The set of closed subsets containing a fixed subset  can be identified with the comma category
can be identified with the comma category 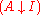 . This category — also a partial order — then has initial object Cl(A). Thus there is a universal arrow from A to I, given by the inclusion
. This category — also a partial order — then has initial object Cl(A). Thus there is a universal arrow from A to I, given by the inclusion  .
.
Similarly, since every closed set containing X \ A corresponds with an open set contained in A we can interpret the category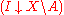 as the set of open subsets contained in A, with terminal object
as the set of open subsets contained in A, with terminal object 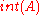 , the interior
, the interior
of A.
All properties of the closure can be derived from this definition and a few properties of the above categories. Moreover, this definition makes precise the analogy between the topological closure and other types of closures (for example algebraic
), since all are examples of universal arrows.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the closure of a subset S in a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure
Adherent point
In mathematics, an adherent point is a slight generalization of the idea of a limit point....
of S. The notion of closure is in many ways dual
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
to the notion of interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
.
Point of closure
For S a subset of a Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, x is a point of closure of S if every open ball centered at x contains a point of S (this point may be x itself).
This definition generalises to any subset S of a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
X. Fully expressed, for X a metric space with metric d, x is a point of closure of S if for every r > 0, there is a y in S such that the distance d(x, y) < r. (Again, we may have x = y.) Another way to express this is to say that x is a point of closure of S if the distance d(x, S) := inf
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
{d(x, s) : s in S} = 0.
This definition generalises to topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s by replacing "open ball" or "ball" with "neighbourhood". Let S be a subset of a topological space X. Then x is a point of closure of S if every neighbourhood of x contains a point of S. Note that this definition does not depend upon whether neighbourhoods are required to be open.
Limit point
The definition of a point of closure is closely related to the definition of a limit pointLimit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
. The difference between the two definitions is subtle but important — namely, in the definition of limit point, every neighborhood of the point x in question must contain a point of the set other than x itself.
Thus, every limit point is a point of closure, but not every point of closure is a limit point. A point of closure which is not a limit point is an isolated point
Isolated point
In topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
. In other words, a point x is an isolated point of S if it is an element of S and if there is a neighbourhood of x which contains no other points of S other than x itself.
For a given set S and point x, x is a point of closure of S if and only if x is an element of S or x is a limit point of S (or both).
Closure of a set
The closure of a set S is the set of all points of closure of S. The closure of S is denoted cl(S), Cl(S), or
or  . The closure of a set has the following properties.
. The closure of a set has the following properties.- cl(S) is a closedClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
superset of S. - cl(S) is the intersection of all closed setClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
s containing S. - cl(S) is the smallest closed set containing S.
- A set S is closed if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
S = cl(S). - If S is a subset of T, then cl(S) is a subset of cl(T).
- If A is a closed set, then A contains S if and only if A contains cl(S).
Sometimes the second or third property above is taken as the definition of the topological closure, which still make sense when applied to other types of closures (see below).
In a first-countable space
First-countable space
In topology, a branch of mathematics, a first-countable space is a topological space satisfying the "first axiom of countability". Specifically, a space X is said to be first-countable if each point has a countable neighbourhood basis...
(such as a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
), cl(S) is the set of all limits
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
of all convergent sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s of points in S. For a general topological space, this statement remains true if one replaces "sequence" by "net
Net (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
" or "filter
Filter (mathematics)
In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
".
Note that these properties are also satisfied if "closure", "superset", "intersection", "contains/containing", "smallest" and "closed" are replaced by "interior", "subset", "union", "contained in", "largest", and "open". For more on this matter, see closure operator below.
Examples
- In any space, the closure of the empty set is the empty set.
- In any space X, X = cl(X).
- If X is the Euclidean space R of real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, then cl((0, 1)) = [0, 1]. - If X is the Euclidean space R, then the closure of the set Q of rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s is the whole space R. We say that Q is dense in R. - If X is the complex planeComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
C = R2, then cl({z in C : |z| > 1}) = {z in C : |z| ≥ 1}. - If S is a finite subset of a Euclidean space, then cl(S) = S. (For a general topological space, this property is equivalent to the T1 axiomT1 spaceIn topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
.)
On the set of real numbers one can put other topologies rather than the standard one.
- If X = R, where R has the lower limit topologyLower limit topologyIn mathematics, the lower limit topology or right half-open interval topology is a topology defined on the set R of real numbers; it is different from the standard topology on R and has a number of interesting properties...
, then cl((0, 1)) =[ 0, 1). - If one considers on R the topology in which every set is open (closed), then cl((0, 1)) = (0, 1).
- If one considers on R the topology in which the only open (closed) sets are the empty set and R itself, then cl((0, 1)) = R.
These examples show that the closure of a set depends upon the topology of the underlying space. The last two examples are special cases of the following.
- In any discrete spaceDiscrete spaceIn topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
, since every set is open (closed), every set is equal to its closure. - In any indiscrete space X, since the only open (closed) sets are the empty set and X itself, we have that the closure of the empty set is the empty set, and for every non-empty subset A of X, cl(A) = X. In other words, every non-empty subset of an indiscrete space is dense.
The closure of a set also depends upon in which space we are taking the closure. For example, if X is the set of rational numbers, with the usual subspace topology
Subspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
induced by the Euclidean space R, and if S = {q in Q : q2 > 2}, then S is closed in Q, and the closure of S in Q is S; however, the closure of S in the Euclidean space R is the set of all real numbers greater than or equal to

Closure operator
The closure operator − is dualDuality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
to the interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
operator o, in the sense that
- S− = X \ (X \ S)o
and also
- So = X \ (X \ S)−
where X denotes the topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
containing S, and the backslash refers to the set-theoretic difference
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
.
Therefore, the abstract theory of closure operators and the Kuratowski closure axioms
Kuratowski closure axioms
In topology and related branches of mathematics, the Kuratowski closure axioms are a set of axioms which can be used to define a topological structure on a set. They are equivalent to the more commonly used open set definition...
can be easily translated into the language of interior operators, by replacing sets with their complements
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
.
Facts about closures
The set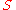 is closed
is closedClosed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
if and only if
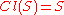 . In particular, the closure of the empty set
. In particular, the closure of the empty setEmpty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
is the empty set, and the closure of
 itself is
itself is  . The closure of an intersection
. The closure of an intersectionIntersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of sets is always a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of (but need not be equal to) the intersection of the closures of the sets. In a union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of finitely many sets, the closure of the union and the union of the closures are equal; the union of zero sets is the empty set, and so this statement contains the earlier statement about the closure of the empty set as a special case. The closure of the union of infinitely many sets need not equal the union of the closures, but it is always a superset
SuperSet
SuperSet Software was a group founded by friends and former Eyring Research Institute co-workers Drew Major, Dale Neibaur, Kyle Powell and later joined by Mark Hurst...
of the union of the closures.
If
 is a subspace of
is a subspace of  containing
containing  , then the closure of
, then the closure of 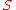 computed in
computed in  is equal to the intersection of
is equal to the intersection of  and the closure of
and the closure of  computed in
computed in  :
: 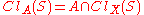 . In particular,
. In particular,  is dense in
is dense in  if and only if
if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
 is a subset of
is a subset of 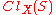 .
.Categorical interpretation
One may elegantly define the closure operator in terms of universal arrows, as follows.The powerset of a set X may be realized as a partial order category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
P in which the objects are subsets and the morphisms are inclusions
 whenever A is a subset of B. Furthermore, a topology T on X is a subcategory of P with inclusion functor
whenever A is a subset of B. Furthermore, a topology T on X is a subcategory of P with inclusion functor  . The set of closed subsets containing a fixed subset
. The set of closed subsets containing a fixed subset  can be identified with the comma category
can be identified with the comma category 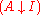 . This category — also a partial order — then has initial object Cl(A). Thus there is a universal arrow from A to I, given by the inclusion
. This category — also a partial order — then has initial object Cl(A). Thus there is a universal arrow from A to I, given by the inclusion  .
.Similarly, since every closed set containing X \ A corresponds with an open set contained in A we can interpret the category
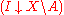 as the set of open subsets contained in A, with terminal object
as the set of open subsets contained in A, with terminal object 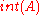 , the interior
, the interiorInterior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
of A.
All properties of the closure can be derived from this definition and a few properties of the above categories. Moreover, this definition makes precise the analogy between the topological closure and other types of closures (for example algebraic
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
), since all are examples of universal arrows.

