
Optimization (mathematics)
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, computational science
Computational science
Computational science is the field of study concerned with constructing mathematical models and quantitative analysis techniques and using computers to analyze and solve scientific problems...
, or management science, mathematical optimization (alternatively, optimization or mathematical programming) refers to the selection of a best element from some set of available alternatives.
In the simplest case, an optimization problem
Optimization problem
In mathematics and computer science, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete...
consists of maximizing or minimizing
Maxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
a real function
Function of a real variable
In mathematics, a function of a real variable is a mathematical function whose domain is the real line. More loosely, a function of a real variable is sometimes taken to mean any function whose domain is a subset of the real line....
by systematically choosing input
Argument of a function
In mathematics, an argument of a function is a specific input in the function, also known as an independent variable. When it is clear from the context which argument is meant, the argument is often denoted by arg....
values from within an allowed set and computing the value
Value (mathematics)
In mathematics, value commonly refers to the 'output' of a function. In the most basic case, that of unary, single-valued functions, there is one input and one output .The function f of the example is real-valued, since each and every possible function value is real...
of the function. The generalization of optimization theory and techniques to other formulations comprises a large area of applied mathematics
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
. More generally, optimization includes finding "best available" values of some objective function given a defined domain, including a variety of different types of objective functions and different types of domains.
Optimization problems
An optimization problem can be represented in the following way- Given: a functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f : A R from some set A to the real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
R from some set A to the real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s - Sought: an element x0 in A such that f(x0) ≤ f(x) for all x in A ("minimization") or such that f(x0) ≥ f(x) for all x in A ("maximization").
Such a formulation is called an optimization problem
Optimization problem
In mathematics and computer science, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete...
or a mathematical programming problem (a term not directly related to computer programming
Computer programming
Computer programming is the process of designing, writing, testing, debugging, and maintaining the source code of computer programs. This source code is written in one or more programming languages. The purpose of programming is to create a program that performs specific operations or exhibits a...
, but still in use for example in linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
- see History below). Many real-world and theoretical problems may be modeled in this general framework. Problems formulated using this technique in the fields of physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
may refer to the technique as energy minimization, speaking of the value of the function f as representing the energy of the system
System
System is a set of interacting or interdependent components forming an integrated whole....
being modeled
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
.
Typically, A is some subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn, often specified by a set of constraint
Constraint (mathematics)
In mathematics, a constraint is a condition that a solution to an optimization problem must satisfy. There are two types of constraints: equality constraints and inequality constraints...
s, equalities or inequalities that the members of A have to satisfy. The domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
A of f is called the search space or the choice set,
while the elements of A are called candidate solution
Candidate solution
In optimization , a candidate solution is a member of a set of possible solutions to a given problem. A candidate solution does not have to be a likely or reasonable solution to the problem – it is simply in the set that satisfies all constraints.The space of all candidate solutions is called the...
s or feasible solutions.
The function f is called, variously, an objective function, cost function (minimization), utility function (maximization), or, in certain fields, energy function, or energy functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
. A feasible solution that minimizes (or maximizes, if that is the goal) the objective function is called an optimal solution.
By convention, the standard form of an optimization problem is stated in terms of minimization. Generally, unless both the objective function and the feasible region are convex in a minimization problem, there may be several local minima, where a local minimum x* is defined as a point for which there exists some δ > 0 so that for all x such that

the expression

holds; that is to say, on some region around x* all of the function values are greater than or equal to the value at that point. Local maxima are defined similarly.
A large number of algorithms proposed for solving non-convex problems – including the majority of commercially available solvers – are not capable of making a distinction between local optimal solutions and rigorous optimal solutions, and will treat the former as actual solutions to the original problem. The branch of applied mathematics
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
and numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
that is concerned with the development of deterministic algorithms that are capable of guaranteeing convergence in finite time to the actual optimal solution of a non-convex problem is called global optimization
Global optimization
Global optimization is a branch of applied mathematics and numerical analysis that deals with the optimization of a function or a set of functions to some criteria.- General :The most common form is the minimization of one real-valued function...
.
Notation
Optimization problems are often expressed with special notation. Here are some examples.Minimum and maximum value of a function
Consider the following notation: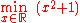
This denotes the minimum value
Value (mathematics)
In mathematics, value commonly refers to the 'output' of a function. In the most basic case, that of unary, single-valued functions, there is one input and one output .The function f of the example is real-valued, since each and every possible function value is real...
of the objective function x2
 , when choosing x from the set of real number
, when choosing x from the set of real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s
 . The minimum value in this case is
. The minimum value in this case is 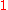 , occurring at
, occurring at  .
.Similarly, the notation
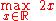
asks for the maximum value of the objective function 2x, where x may be any real number. In this case, there is no such maximum as the objective function is unbounded, so the answer is "infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
" or "undefined".
Optimal input arguments
Consider the following notation: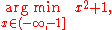
or equivalently

This represents the value (or values) of the argument
Argument of a function
In mathematics, an argument of a function is a specific input in the function, also known as an independent variable. When it is clear from the context which argument is meant, the argument is often denoted by arg....
x in the interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
 that minimizes (or minimize) the objective function x2 + 1 (the actual minimum value of that function is not what the problem asks for). In this case, the answer is x = -1, since x = 0 is infeasible, i.e. does not belong to the feasible set.
that minimizes (or minimize) the objective function x2 + 1 (the actual minimum value of that function is not what the problem asks for). In this case, the answer is x = -1, since x = 0 is infeasible, i.e. does not belong to the feasible set.Similarly,
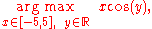
or equivalently

represents the
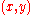 pair (or pairs) that maximizes (or maximize) the value of the objective function
pair (or pairs) that maximizes (or maximize) the value of the objective function  , with the added constraint that x lie in the interval
, with the added constraint that x lie in the interval 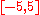 (again, the actual maximum value of the expression does not matter). In this case, the solutions are the pairs of the form (5, 2kπ
(again, the actual maximum value of the expression does not matter). In this case, the solutions are the pairs of the form (5, 2kπPi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
) and (−5,(2k+1)π), where k ranges over all integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s.
Arg min and arg max are sometimes also written argmin and argmax, and stand for argument of the minimum and argument of the maximum.
History
FermatPierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
and Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
found calculus-based formulas for identifying optima, while Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
and Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
proposed iterative methods for moving towards an optimum. Historically, the first term for optimization was "linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
", which was due to George B. Dantzig
George Dantzig
George Bernard Dantzig was an American mathematical scientist who made important contributions to operations research, computer science, economics, and statistics....
, although much of the theory had been introduced by Leonid Kantorovich
Leonid Kantorovich
Leonid Vitaliyevich Kantorovich was a Soviet mathematician and economist, known for his theory and development of techniques for the optimal allocation of resources...
in 1939. Dantzig published the Simplex algorithm
Simplex algorithm
In mathematical optimization, Dantzig's simplex algorithm is a popular algorithm for linear programming. The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century....
in 1947, and John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
developed the theory of duality in the same year.
The term programming in this context does not refer to computer programming
Computer programming
Computer programming is the process of designing, writing, testing, debugging, and maintaining the source code of computer programs. This source code is written in one or more programming languages. The purpose of programming is to create a program that performs specific operations or exhibits a...
. Rather, the term comes from the use of program by the United States military to refer to proposed training and logistics
Logistics
Logistics is the management of the flow of goods between the point of origin and the point of destination in order to meet the requirements of customers or corporations. Logistics involves the integration of information, transportation, inventory, warehousing, material handling, and packaging, and...
schedules, which were the problems Dantzig studied at that time.
Later important researchers in mathematical optimization include the following:
- Richard BellmanRichard BellmanRichard Ernest Bellman was an American applied mathematician, celebrated for his invention of dynamic programming in 1953, and important contributions in other fields of mathematics.-Biography:...
- Ronald A. HowardRonald A. HowardRonald A. Howard has been a professor at Stanford University since 1965. In 1964 he defined the profession of decision analysis, and since then has been developing the field as professor in the Department of Engineering-Economic Systems in the School of Engineering at Stanford.Howard directs...
- Narendra KarmarkarNarendra KarmarkarNarendra K. Karmarkar is an Indian mathematician, renowned for developing Karmarkar's algorithm. He is listed as an ISI highly cited researcher.- Biography :...
- William KarushWilliam KarushWilliam Karush was a professor emeritus of California State University at Northridge and is a mathematician best known for his contribution to Karush–Kuhn–Tucker conditions...
- Leonid KhachiyanLeonid KhachiyanLeonid Genrikhovich Khachiyan was a Soviet mathematician of Armenian descent who taught Computer Science at Rutgers University. He was most famous for his Ellipsoid algorithm for linear programming, which was the first such algorithm known to have a polynomial running time...
- Bernard KoopmanBernard KoopmanBernard Osgood Koopman was a French-born American mathematician, known for his work in ergodic theory, the foundations of probability, statistical theory and operations research....
- Harold Kuhn
- Joseph Louis LagrangeJoseph Louis LagrangeJoseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
- László LovászLászló LovászLászló Lovász is a Hungarian mathematician, best known for his work in combinatorics, for which he was awarded the Wolf Prize and the Knuth Prize in 1999, and the Kyoto Prize in 2010....
- Arkadii Nemirovskii
- Yurii Nesterov
- Boris Polyak
- Lev Pontryagin
- James Renegar
- R. Tyrrell RockafellarR. Tyrrell Rockafellar* for the George Dantzig Prize in 1994 in Optima, Issue 44 page 5.- Books :* Rockafellar, R. Tyrrell. Conjugate duality and optimization. Lectures given at the Johns Hopkins University, Baltimore, Md., June, 1973. Conference Board of the Mathematical Sciences Regional Conference Series in Applied...
- Cornelis Roos
- Naum Z. ShorNaum Z. ShorNaum Zuselevich Shor was a Soviet and Ukrainian Jewish mathematician specializing in optimization.He made significant contributions to nonlinear and stochastic programming, numerical techniques for non-smooth optimization, discrete optimization problems, matrix optimization, dual quadratic bounds...
- Michael J. Todd
- Albert TuckerAlbert W. TuckerAlbert William Tucker was a Canadian-born American mathematician who made important contributions in topology, game theory, and non-linear programming....
Major subfields
- Convex programming studies the case when the objective function is convexConvex functionIn mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
(minimization) or concaveConcave functionIn mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.-Definition:...
(maximization) and the constraint set is convexConvex setIn Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
. This can be viewed as a particular case of nonlinear programming or as generalization of linear or convex quadratic programming.- Linear programmingLinear programmingLinear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
(LP), a type of convex programming, studies the case in which the objective function f is linear and the set of constraints is specified using only linear equalities and inequalities. Such a set is called a polyhedronPolyhedronIn elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
or a polytopePolytopeIn elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
if it is boundedBounded setIn mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
. - Second order cone programming (SOCP) is a convex program, and includes certain types of quadratic programs.
- Semidefinite programmingSemidefinite programmingSemidefinite programming is a subfield of convex optimization concerned with the optimization of a linear objective functionover the intersection of the cone of positive semidefinite matrices with an affine space, i.e., a spectrahedron....
(SDP) is a subfield of convex optimization where the underlying variables are semidefinite matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. It is generalization of linear and convex quadratic programming. - Conic programming is a general form of convex programming. LP, SOCP and SDP can all be viewed as conic programs with the appropriate type of cone.
- Geometric programming is a technique whereby objective and inequality constraints expressed as posynomials and equality constraints as monomials can be transformed into a convex program.
- Linear programming
- Integer programmingInteger programmingAn integer programming problem is a mathematical optimization or feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming, which is also known as mixed integer programming.Integer programming is NP-hard...
studies linear programs in which some or all variables are constrained to take on integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
values. This is not convex, and in general much more difficult than regular linear programming. - Quadratic programmingQuadratic programmingQuadratic programming is a special type of mathematical optimization problem. It is the problem of optimizing a quadratic function of several variables subject to linear constraints on these variables....
allows the objective function to have quadratic terms, while the feasible set must be specified with linear equalities and inequalities. For specific forms of the quadratic term, this is a type of convex programming. - Fractional programmingFractional programmingIn mathematical optimization, fractional programming is a generalization of linear-fractional programming. The objective function in a fractional program is a ratio of two functions that are in general nonlinear...
studies optimization of ratios of two nonlinear functions. The special class of concave fractional programs can be transformed to a convex optimization problem. - Nonlinear programmingNonlinear programmingIn mathematics, nonlinear programming is the process of solving a system of equalities and inequalities, collectively termed constraints, over a set of unknown real variables, along with an objective function to be maximized or minimized, where some of the constraints or the objective function are...
studies the general case in which the objective function or the constraints or both contain nonlinear parts. This may or may not be a convex program. In general, whether the program is convex affects the difficulty of solving it. - Stochastic programmingStochastic programmingStochastic programming is a framework for modeling optimization problems that involve uncertainty. Whereas deterministic optimization problems are formulated with known parameters, real world problems almost invariably include some unknown parameters. When the parameters are known only within...
studies the case in which some of the constraints or parameters depend on random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s. - Robust programmingRobust optimizationRobust optimization is a field of optimization theory that deals with optimization problems where robustness is sought against uncertainty and/or variability in the value of a parameter of the problem.- History :...
is, like stochastic programming, an attempt to capture uncertainty in the data underlying the optimization problem. This is not done through the use of random variables, but instead, the problem is solved taking into account inaccuracies in the input data. - Combinatorial optimizationCombinatorial optimizationIn applied mathematics and theoretical computer science, combinatorial optimization is a topic that consists of finding an optimal object from a finite set of objects. In many such problems, exhaustive search is not feasible...
is concerned with problems where the set of feasible solutions is discrete or can be reduced to a discreteDiscrete mathematicsDiscrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...
one. - Infinite-dimensional optimizationInfinite-dimensional optimizationIn certain optimization problems the unknown optimal solution might not be a number or a vector, but rather a continuous quantity, for example a function or the shape of a body...
studies the case when the set of feasible solutions is a subset of an infinite-dimensionDimensionIn physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al space, such as a space of functions. - MetaheuristicMetaheuristicIn computer science, metaheuristic designates a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. Metaheuristics make few or no assumptions about the problem being optimized and can search very large spaces...
s make few or no assumptions about the problem being optimized and can search very large spaces of candidate solutions. However, metaheuristics do not guarantee an optimal solution is ever found. - Constraint satisfactionConstraint satisfactionIn artificial intelligence and operations research, constraint satisfaction is the process of finding a solution to a set of constraints that impose conditions that the variables must satisfy. A solution is therefore a vector of variables that satisfies all constraints.The techniques used in...
studies the case in which the objective function f is constant (this is used in artificial intelligenceArtificial intelligenceArtificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
, particularly in automated reasoningAutomated reasoningAutomated reasoning is an area of computer science dedicated to understand different aspects of reasoning. The study in automated reasoning helps produce software which allows computers to reason completely, or nearly completely, automatically...
).- Constraint programmingConstraint programmingConstraint programming is a programming paradigm wherein relations between variables are stated in the form of constraints. Constraints differ from the common primitives of imperative programming languages in that they do not specify a step or sequence of steps to execute, but rather the properties...
.
- Constraint programming
- Disjunctive programming is used where at least one constraint must be satisfied but not all. It is of particular use in scheduling.
In a number of subfields, the techniques are designed primarily for optimization in dynamic contexts (that is, decision making over time):
- Calculus of variationsCalculus of variationsCalculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
seeks to optimize an objective defined over many points in time, by considering how the objective function changes if there is a small change in the choice path. - Optimal controlOptimal controlOptimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
theory is a generalization of the calculus of variations. - Dynamic programmingDynamic programmingIn mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
studies the case in which the optimization strategy is based on splitting the problem into smaller subproblems. The equation that describes the relationship between these subproblems is called the Bellman equationBellman equationA Bellman equation , named after its discoverer, Richard Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming...
. - Mathematical programming with equilibrium constraintsMathematical programming with equilibrium constraintsMathematical programming with equilibrium constraints is the study ofconstrained optimization problems where the constraints include variational inequalities or complementarities...
is where the constraints include variational inequalities or complementaritiesComplementarity theoryA complementarity problem is a type of mathematical optimization problem. It is the problem of optimizing a function of two vector variables subject to certain requirements which include: that the inner product of the two variables must equal zero, i.e. = 0...
.
Multi-objective optimization
Adding more than one objective to an optimization problem adds complexity. For example, to optimize a structural design, one would want a design that is both light and rigid. Because these two objectives conflict, a trade-off exists. There will be one lightest design, one stiffest design, and an infinite number of designs that are some compromise of weight and stiffness. The set of trade-off designs that cannot be improved upon according to one criterion without hurting another criterion is known as the Pareto set. The curve created plotting weight against stiffness of the best designs is known as the Pareto frontier.A design is judged to be "Pareto optimal" (equivalently, "Pareto efficient" or in the Pareto set) if it is not dominated by any other design: If it is worse than another design in some respects and no better in any respect, then it is dominated and is not Pareto optimal.
Multi-modal optimization
Optimization problems are often multi-modal; that is they possess multiple good solutions. They could all be globally good (same cost function value) or there could be a mix of globally good and locally good solutions. Obtaining all (or at least some of) the multiple solutions is the goal of a multi-modal optimizer.Classical optimization techniques due to their iterative approach do not perform satisfactorily when they are used to obtain multiple solutions, since it is not guaranteed that different solutions will be obtained even with different starting points in multiple runs of the algorithm. Evolutionary Algorithm
Evolutionary algorithm
In artificial intelligence, an evolutionary algorithm is a subset of evolutionary computation, a generic population-based metaheuristic optimization algorithm. An EA uses some mechanisms inspired by biological evolution: reproduction, mutation, recombination, and selection...
s are however a very popular approach to obtain multiple solutions in a multi-modal optimization task. See Evolutionary multi-modal optimization
Evolutionary multi-modal optimization
In applied mathematics, multimodal optimization deals with Optimization tasks that involve finding all or most of the multiple solutions . Knowledge of multiple solutions to an optimization task is especially helpful in engineering, when due to physical constraints, the best results may not...
.
Feasibility problem
The satisfiability problem, also called the feasibility problem, is just the problem of finding any feasible solution at all without regard to objective value. This can be regarded as the special case of mathematical optimization where the objective value is the same for every solution, and thus any solution is optimal.Many optimization algorithms need to start from a feasible point. One way to obtain such a point is to relax the feasibility conditions using a slack variable
Slack variable
In an optimization problem, a slack variable is a variable that is added to an inequality constraint to transform it to an equality. Introducing a slack variable replaces an inequality constraint with an equality constraint and a nonnegativity constraint....
; with enough slack, any starting point is feasible. Then, minimize that slack variable until slack is null or negative.
Existence
The extreme value theoremExtreme value theorem
In calculus, the extreme value theorem states that if a real-valued function f is continuous in the closed and bounded interval [a,b], then f must attain its maximum and minimum value, each at least once...
of Karl Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
states that a continuous real-valued function on a compact set attains its maximum and minimum value. More generally, a lower semi-continuous function on a compact set attains its minimum; an upper semi-continuous function on a compact set attains its maximum.
Necessary conditions for optimality
One of Fermat's theoremsFermat's theorem (stationary points)
In mathematics, Fermat's theorem is a method to find local maxima and minima of differentiable functions on open sets by showing that every local extremum of the function is a stationary point...
states that optima of unconstrained problems are found at stationary point
Stationary point
In mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
s, where the first derivative or the gradient of the objective function is zero (see first derivative test
First derivative test
In calculus, the first derivative test uses the first derivative of a function to determine whether a given critical point of a function is a local maximum, a local minimum, or neither.-Intuitive explanation:...
). More generally, they may be found at critical points
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
, where the first derivative or gradient of the objective function is zero or is undefined, or on the boundary of the choice set. An equation (or set of equations) stating that the first derivative(s) equal(s) zero at an interior optimum is called a 'first-order condition' or a set of first-order conditions.
Optima of inequality-constrained problems are instead found by the Lagrange multiplier method. This method calculates a system of inequalities called the 'Karush–Kuhn–Tucker conditions' or 'complementary slackness conditions', which may then be used to calculate the optimum.
Sufficient conditions for optimality
While the first derivative test identifies points that might be optima, this test does not distinguish a point which is a minimum from one that is a maximum or one that is neither. When the objective function is twice differentiable, these cases can be distinguished by checking the second derivative or the matrix of second derivatives (called the Hessian matrixHessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
) in unconstrained problems, or the matrix of second derivatives of the objective function and the constraints called the bordered Hessian in constrained problems. The conditions that distinguish maxima, or minima, from other stationary points are called 'second-order conditions' (see 'Second derivative test
Second derivative test
In calculus, the second derivative test is a criterion often useful for determining whether a given stationary point of a function is a local maximum or a local minimum using the value of the second derivative at the point....
'). If a candidate solution satisfies the first-order conditions, then satisfaction of the second-order conditions as well is sufficient to establish at least local optimality.
Sensitivity and continuity of optima
The envelope theoremEnvelope theorem
The envelope theorem is a theorem about optimization problems in microeconomics. It may be used to prove Hotelling's lemma, Shephard's lemma, and Roy's identity...
describes how the value of an optimal solution changes when an underlying parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
changes. The process of computing this change is called comparative statics
Comparative statics
In economics, comparative statics is the comparison of two different economic outcomes, before and after a change in some underlying exogenous parameter....
.
The maximum theorem
Maximum theorem
The maximum theorem provides conditions for the continuity of an optimized function and the set of its maximizers as a parameter changes. The statement was first proven by Claude Berge in 1959...
of Claude Berge
Claude Berge
Claude Berge was a French mathematician, recognized as one of the modern founders of combinatorics and graph theory. He is particularly remembered for his famous conjectures on perfect graphs and for Berge's lemma, which states that a matching M in a graph G is maximum if and only if there is in...
(1963) describes the continuity of an optimal solution as a function of underlying parameters.
Calculus of optimization
For unconstrained problems with twice-differentiable functions, some critical pointCritical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
s can be found by finding the points where the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of the objective function is zero (that is, the stationary points). More generally, a zero subgradient certifies that a local minimum has been found for minimization problems with convex function
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
s and other locally
Rademacher's theorem
In mathematical analysis, Rademacher's theorem, named after Hans Rademacher, states the following: If U is an open subset of Rn andis Lipschitz continuous, then f is Fréchet-differentiable almost everywhere in U In mathematical analysis, Rademacher's theorem, named after Hans Rademacher, states the...
Lipschitz functions.
Further, critical points can be classified using the definiteness of the Hessian matrix
Hessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
: If the Hessian is positive definite at a critical point, then the point is a local minimum; if the Hessian matrix is negative definite, then the point is a local maximum; finally, if indefinite, then the point is some kind of saddle point
Saddle point
In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
.
Constrained problems can often be transformed into unconstrained problems with the help of Lagrange multipliers. Lagrangian relaxation
Lagrangian relaxation
In the field of mathematical optimization, Lagrangian relaxation is a relaxation method which approximates a difficult problem of constrained optimization by a simpler problem...
can also provide approximate solutions to difficult constrained problems.
When the objective function is convex
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
, then any local minimum will also be a global minimum. There exist efficient numerical techniques for minimizing convex functions, such as interior-point methods.
Computational optimization techniques
To solve problems, researchers may use algorithmAlgorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s that terminate in a finite number of steps, or iterative method
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
s that converge to a solution (on some specified class of problems), or heuristics that may provide approximate solutions to some problems (although their iterates need not converge).
Optimization algorithms
- Simplex algorithmSimplex algorithmIn mathematical optimization, Dantzig's simplex algorithm is a popular algorithm for linear programming. The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century....
of George DantzigGeorge DantzigGeorge Bernard Dantzig was an American mathematical scientist who made important contributions to operations research, computer science, economics, and statistics....
, designed for linear programmingLinear programmingLinear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
. - Extensions of the simplex algorithm, designed for quadratic programmingQuadratic programmingQuadratic programming is a special type of mathematical optimization problem. It is the problem of optimizing a quadratic function of several variables subject to linear constraints on these variables....
and for linear-fractional programmingLinear-fractional programmingIn mathematical optimization, linear-fractional programming is a generalization of linear programming . Whereas the objective function in linear programs are linear functions, the objective function in a linear-fractional program is a ratio of two linear functions...
. - Variants of the simplex algorithm that are especially suited for network optimizationFlow networkIn graph theory, a flow network is a directed graph where each edge has a capacity and each edge receives a flow. The amount of flow on an edge cannot exceed the capacity of the edge. Often in Operations Research, a directed graph is called a network, the vertices are called nodes and the edges are...
. - Combinatorial algorithmCombinatorial optimizationIn applied mathematics and theoretical computer science, combinatorial optimization is a topic that consists of finding an optimal object from a finite set of objects. In many such problems, exhaustive search is not feasible...
s
Iterative methods
The iterative methods used to solve problems of nonlinear programmingNonlinear programming
In mathematics, nonlinear programming is the process of solving a system of equalities and inequalities, collectively termed constraints, over a set of unknown real variables, along with an objective function to be maximized or minimized, where some of the constraints or the objective function are...
differ according to whether they evaluate
Subroutine
In computer science, a subroutine is a portion of code within a larger program that performs a specific task and is relatively independent of the remaining code....
Hessians, gradients, or only function values. While evaluating Hessians (H) and gradients (G) improves the rate of convergence, such evaluations increase the computational complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
(or computational cost) of each iteration. In some cases, the computational complexity may be excessively high.
One major criterion for optimizers is just the number of required function evaluations as this often is already a large computational effort, usually much more effort than within the optimizer itself, which mainly has to operate over the N variables.
The derivatives provide detailed information for such optimizers, but are even harder to calculate, e.g. approximating the gradient takes at least N+1 function evaluations. For approximations of the 2nd derivatives (collected in the Hessian matrix) the number of function evaluations is in the order of N². Newton's method requires the 2nd order derivates, so for each iteration the number of function calls is in the order of N², but for a simpler pure gradient optimizer it is only N. However, gradient optimizers need usually more iterations than Newton's algorithm. Which one is best wrt. number of function calls depends on the problem itself.
- Methods that evaluate Hessians (or approximate Hessians, using finite differenceFinite differenceA finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
s):- Newton's methodNewton's method in optimizationIn mathematics, Newton's method is an iterative method for finding roots of equations. More generally, Newton's method is used to find critical points of differentiable functions, which are the zeros of the derivative function.-Method:...
- Sequential quadratic programmingSequential quadratic programmingSequential quadratic programming is an iterative method for nonlinear optimization. SQP methods are used on problems for which the objective function and the constraints are twice continuously differentiable....
: A method for small-medium scale constrained problems. Some versions can handle large-dimensional problems.
- Newton's method
- Methods that evaluate gradients or approximate gradients using finite differences (or even subgradients):
- Quasi-Newton methodQuasi-Newton methodIn optimization, quasi-Newton methods are algorithms for finding local maxima and minima of functions. Quasi-Newton methods are based on...
s: Iterative methods for medium-large problems (e.g. N<1000). - Conjugate gradient methodConjugate gradient methodIn mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is symmetric and positive-definite. The conjugate gradient method is an iterative method, so it can be applied to sparse systems that are too...
s: Iterative methodIterative methodIn computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
s for large problems. (In theory, these methods terminate in a finite number of steps with quadratic objective functions, but this finite termination is not observed in practice on finite–precision computers.) - Interior point methods: This is a large class of methods for constrained optimization. Some interior-point methods use only (sub)gradient information, and others of which require the evaluation of Hessians.
- Gradient descentGradient descentGradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient of the function at the current point...
(alternatively, "steepest descent" or "steepest ascent"): A (slow) method of historical and theoretical interest, which has had renewed interest for finding approximate solutions of enormous problems. - Subgradient methodSubgradient methodSubgradient methods are iterative methods for solving convex minimization problems. Originally developed by Naum Z. Shor and others in the 1960s and 1970s, subgradient methods are convergent when applied even to a non-differentiable objective function...
s - An iterative method for large locallyRademacher's theoremIn mathematical analysis, Rademacher's theorem, named after Hans Rademacher, states the following: If U is an open subset of Rn andis Lipschitz continuous, then f is Fréchet-differentiable almost everywhere in U In mathematical analysis, Rademacher's theorem, named after Hans Rademacher, states the...
Lipschitz functionLipschitz continuityIn mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
s using generalized gradients. Following Boris T. Polyak, subgradient–projection methods are similar to conjugate–gradient methods. - Bundle method of descent: An iterative method for small–medium sized problems with locally Lipschitz functions, particularly for convex minimization problems. (Similar to conjugate gradient methods)
- Ellipsoid methodEllipsoid methodIn mathematical optimization, the ellipsoid method is an iterative method for minimizing convex functions. When specialized to solving feasible linear optimization problems with rational data, the ellipsoid method is an algorithm, which finds an optimal solution in a finite number of steps.The...
: An iterative method for small problems with quasiconvexQuasiconvex functionIn mathematics, a quasiconvex function is a real-valued function defined on an interval or on a convex subset of a real vector space such that the inverse image of any set of the form is a convex set...
objective functions and of great theoretical interest, particularly in establishing the polynomial time complexity of some combinatorial optimization problems. It has similarities with Quasi-Newton methods. - Reduced gradient method (Frank–Wolfe)Frank–Wolfe algorithmIn mathematical optimization, the reduced gradient method of Frank and Wolfe is an iterative method for nonlinear programming. Also known as the Frank–Wolfe algorithm and the convex combination algorithm, the reduced gradient method was proposed by Marguerite Frank and Phil Wolfe in 1956 as an...
for approximate minimization of specially structured problems with linear constraints, especially with traffic networks. For general unconstrained problems, this method reduces to the gradient method, which is regarded as obsolete (for almost all problems).
- Quasi-Newton method
- Methods that evaluate only function values: If a problem is continuously differentiable, then gradients can be approximated using finite differences, in which case a gradient-based method can be used. Usually such non-gradient methods work only fine for problems with few parameter only.
- InterpolationInterpolationIn the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
methods - Pattern searchPattern search (optimization)Pattern search is a family of numerical optimization methods that do not require the gradient of the problem to be optimized. Hence PS can be used on functions that are not continuous or differentiable. Such optimization methods are also known as direct-search, derivative-free, or black-box...
methods, which have better convergence properties than the Nelder–Mead simplicial heuristic (listed below, under heuristics).
- Interpolation
Global convergence
More generally, if the objective function is not a quadratic function, then many optimization methods use other methods to ensure that some subsequence of iterations converges to an optimal solution. The first and still popular method for ensuring convergence relies on-line searches, which optimize a function along one dimension. A second and increasingly popular method for ensuring convergence uses trust regionTrust region
Trust region is a term used in mathematical optimization to denote the subset of the region of the objective function to be optimized that is approximated using a model function . If an adequate model of the objective function is found within the trust region then the region is expanded;...
s. Both line searches and trust regions are used in modern methods of non-differentiable optimization
Subgradient method
Subgradient methods are iterative methods for solving convex minimization problems. Originally developed by Naum Z. Shor and others in the 1960s and 1970s, subgradient methods are convergent when applied even to a non-differentiable objective function...
. Usually a global optimizer is much slower than advanced local optimizers (such as BFGS), so often an efficient global optimizer can be constructed by starting the local optimizer from different starting points.
Heuristics
Besides (finitely terminating) algorithmAlgorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s and (convergent) iterative method
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
s, there are heuristics that can provide approximate solutions to some optimization problems:
- Memetic algorithmMemetic algorithmMemetic algorithms represent one of the recent growing areas of research in evolutionary computation. The term MA is now widely used as a synergy of evolutionary or any population-based approach with separate individual learning or local improvement procedures for problem search...
- Differential evolutionDifferential evolutionIn computer science, differential evolution is a method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. Such methods are commonly known as metaheuristics as they make few or no assumptions about the problem being optimized...
- Dynamic relaxationDynamic relaxationDynamic relaxation is a numerical method, which, among other things, can be used do "form-finding" for cable and fabric structures. The aim is to find a geometry where all forces are in equilibrium...
- Genetic algorithms
- Hill climbingHill climbingIn computer science, hill climbing is a mathematical optimization technique which belongs to the family of local search. It is an iterative algorithm that starts with an arbitrary solution to a problem, then attempts to find a better solution by incrementally changing a single element of the solution...
- Nelder-Mead simplicial heuristicNelder-Mead methodThe Nelder–Mead method or downhill simplex method or amoeba method is a commonly used nonlinear optimization technique, which is a well-defined numerical method for twice differentiable and unimodal problems...
: A popular heuristic for approximate minimization (without calling gradients) - Particle swarm optimizationParticle swarm optimizationIn computer science, particle swarm optimization is a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality...
- Simulated annealingSimulated annealingSimulated annealing is a generic probabilistic metaheuristic for the global optimization problem of locating a good approximation to the global optimum of a given function in a large search space. It is often used when the search space is discrete...
- Tabu searchTabu searchTabu search is a mathematical optimization method, belonging to the class of trajectory based techniques. Tabu search enhances the performance of a local search method by using memory structures that describe the visited solutions: once a potential solution has been determined, it is marked as...
Mechanics and engineering
Problems in rigid body dynamicsRigid body dynamics
In physics, rigid body dynamics is the study of the motion of rigid bodies. Unlike particles, which move only in three degrees of freedom , rigid bodies occupy space and have geometrical properties, such as a center of mass, moments of inertia, etc., that characterize motion in six degrees of...
(in particular articulated rigid body dynamics) often require mathematical programming techniques, since you can view rigid body dynamics as attempting to solve an ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
on a constraint manifold; the constraints are various nonlinear geometric constraints such as "these two points must always coincide", "this surface must not penetrate any other", or "this point must always lie somewhere on this curve". Also, the problem of computing contact forces can be done by solving a linear complementarity problem
Linear complementarity problem
In mathematical optimization theory, the linear complementarity problem arises frequently in computational mechanics and encompasses the well-known quadratic programming as a special case...
, which can also be viewed as a QP (quadratic programming) problem.
Many design problems can also be expressed as optimization programs. This application is called design optimization. One subset is the engineering optimization
Engineering optimization
Engineering Optimization is the subject which uses optimization techniques to achieve design goals in engineering.It is also called design optimization. Its topics include structural design , shape optimization, topological optimization , inverse optimization, processing planning, product designs...
, and another recent and growing subset of this field is multidisciplinary design optimization
Multidisciplinary design optimization
Multi-disciplinary design optimization is a field of engineering that uses optimization methods to solve design problems incorporating a number of disciplines. As defined by Prof. Carlo Poloni, MDO is "the art of finding the best compromise"...
, which, while useful in many problems, has in particular been applied to aerospace engineering
Aerospace engineering
Aerospace engineering is the primary branch of engineering concerned with the design, construction and science of aircraft and spacecraft. It is divided into two major and overlapping branches: aeronautical engineering and astronautical engineering...
problems.
Economics
EconomicsEconomics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
is closely enough linked to optimization of agents
Agent (economics)
In economics, an agent is an actor and decision maker in a model. Typically, every agent makes decisions by solving a well or ill defined optimization/choice problem. The term agent can also be seen as equivalent to player in game theory....
that an influential definition relatedly describes economics qua science as the "study of human behavior as a relationship between ends and scarce means" with alternative uses. Modern optimization theory includes traditional optimization theory but also overlaps with game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
and the study of economic equilibria. The Journal of Economic Literature
Journal of Economic Literature
The Journal of Economic Literature is a peer-reviewed academic journal on economy published by the American Economic Association. It was established in 1963 as the Journal of Economic Abstracts. As a review journal, it mainly features essays and reviews of recent economic theories...
codes
JEL classification codes
Articles in economics journals are usually classified according to the JEL classification codes, a system originated by the Journal of Economic Literature. The JEL is published quarterly by the American Economic Association and contains survey articles and information on recently published books...
classify mathematical programming, optimization techniques, and related topics under JEL:C61-C63.
In microeconomics, the utility maximization problem
Utility maximization problem
In microeconomics, the utility maximization problem is the problem consumers face: "how should I spend my money in order to maximize my utility?" It is a type of optimal decision problem.-Basic setup:...
and its dual problem
Dual problem
In constrained optimization, it is often possible to convert the primal problem to a dual form, which is termed a dual problem. Usually dual problem refers to the Lagrangian dual problem but other dual problems are used, for example, the Wolfe dual problem and the Fenchel dual problem...
, the expenditure minimization problem
Expenditure minimization problem
In microeconomics, the expenditure minimization problem is another perspective on the utility maximization problem: "how much money do I need to reach a certain level of happiness?". This question comes in two parts...
, are economic optimization problems. Insofar as they behave consistently, consumer
Consumer
Consumer is a broad label for any individuals or households that use goods generated within the economy. The concept of a consumer occurs in different contexts, so that the usage and significance of the term may vary.-Economics and marketing:...
s are assumed to maximize their utility
Utility
In economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service....
, while firm
Firm
A firm is a business.Firm or The Firm may also refer to:-Organizations:* Hooligan firm, a group of unruly football fans* The Firm, Inc., a talent management company* Fair Immigration Reform Movement...
s are usually assumed to maximize their profit
Profit (economics)
In economics, the term profit has two related but distinct meanings. Normal profit represents the total opportunity costs of a venture to an entrepreneur or investor, whilst economic profit In economics, the term profit has two related but distinct meanings. Normal profit represents the total...
. Also, agents are often modeled as being risk-averse, thereby preferring to avoid risk. Asset prices are also modeled using optimization theory, though the underlying mathematics relies on optimizing stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
es rather than on static optimization. Trade
Trade
Trade is the transfer of ownership of goods and services from one person or entity to another. Trade is sometimes loosely called commerce or financial transaction or barter. A network that allows trade is called a market. The original form of trade was barter, the direct exchange of goods and...
theory also uses optimization to explain trade patterns between nations.
Since the 1970s, economists have modeled dynamic decisions over time using control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
. For example, microeconomists use dynamic
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
search model
Search theory
In microeconomics, search theory studies buyers or sellers who cannot instantly find a trading partner, and must therefore search for a partner prior to transacting....
s to study labor-market behavior. A crucial distinction is between deterministic and stochastic models. Macroeconomists
Macroeconomics
Macroeconomics is a branch of economics dealing with the performance, structure, behavior, and decision-making of the whole economy. This includes a national, regional, or global economy...
build dynamic stochastic general equilibrium (DSGE)
Dynamic stochastic general equilibrium
Dynamic stochastic general equilibrium modeling is a branch of applied general equilibrium theory that is influential in contemporary macroeconomics...
models that describe the dynamics of the whole economy as the result of the interdependent optimizing decisions of workers, consumers, investors, and governments.
Operations research
Another field that uses optimization techniques extensively is operations researchOperations research
Operations research is an interdisciplinary mathematical science that focuses on the effective use of technology by organizations...
. Operations research also uses stochastic modeling and simulation to support improved decision-making. Increasingly, operations research uses stochastic programming
Stochastic programming
Stochastic programming is a framework for modeling optimization problems that involve uncertainty. Whereas deterministic optimization problems are formulated with known parameters, real world problems almost invariably include some unknown parameters. When the parameters are known only within...
to model dynamic decisions that adapt to events; such problems can be solved with large-scale optimization and stochastic optimization
Stochastic optimization
Stochastic optimization methods are optimization methods that generate and use random variables. For stochastic problems, the random variables appear in the formulation of the optimization problem itself, which involve random objective functions or random constraints, for example. Stochastic...
methods.
See also
- Curve fittingCurve fittingCurve fitting is the process of constructing a curve, or mathematical function, that has the best fit to a series of data points, possibly subject to constraints. Curve fitting can involve either interpolation, where an exact fit to the data is required, or smoothing, in which a "smooth" function...
- Arg max
- Brachistochrone
- Fuzzy logicFuzzy logicFuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
- Game theoryGame theoryGame theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
- Engineering optimizationEngineering optimizationEngineering Optimization is the subject which uses optimization techniques to achieve design goals in engineering.It is also called design optimization. Its topics include structural design , shape optimization, topological optimization , inverse optimization, processing planning, product designs...
- Goal programmingGoal programmingGoal programming is a branch of multiobjective optimization, which in turn is a branch of multi-criteria decision analysis , also known as multiple-criteria decision making . This is an optimization programme. It can be thought of as an extension or generalisation of linear programming to handle...
- Important publications in optimization
- Interval finite elementInterval finite elementThe interval finite element method is a finite element method that uses interval parameters. Interval FEM can be applied in situations where it is not possible to get reliable probabilistic characteristics of the structure. This is important in concrete structures, wood structures, geomechanics,...
- Least squaresLeast squaresThe method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
- MetaheuristicMetaheuristicIn computer science, metaheuristic designates a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. Metaheuristics make few or no assumptions about the problem being optimized and can search very large spaces...
- Mathematical Optimization Society (formerly Mathematical Programming Society)
- Mathematical optimization software
- Optimization algorithms
- Optimization problemOptimization problemIn mathematics and computer science, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete...
- Process optimizationProcess optimizationProcess optimization is the discipline of adjusting a process so as to optimize some specified set of parameters without violating some constraint. The most common goals are minimizing cost, maximizing throughput, and/or efficiency...
- Radial basis functionRadial basis functionA radial basis function is a real-valued function whose value depends only on the distance from the origin, so that \phi = \phi; or alternatively on the distance from some other point c, called a center, so that \phi = \phi...
- Random optimizationRandom optimizationRandom optimization is a family of numerical optimization methods that do not require the gradient of the problem to be optimized and RO can hence be used on functions that are not continuous or differentiable...
- Topkis's theoremTopkis's TheoremIn mathematical economics, Topkis's theorem is a result that is useful for establishing comparative statics. The theorem allows researchers to understand how the optimal value for a choice variable changes when a feature of the environment changes...
- Variational calculus
Graduate level
-
- J. E. Dennis, Jr. and Robert B. Schnabel, A view of unconstrained optimization (pp. 1–72);
- Donald Goldfarb and Michael J. Todd, Linear programming (pp. 73–170);
- Philip E. Gill, Walter Murray, Michael A. Saunders, and Margaret H. Wright, Constrained nonlinear programming (pp. 171–210);
- Ravindra K. AhujaRavindra K. AhujaDr. Ravindra K. Ahuja is a researcher and academician. He has contributed to the theory and applications of network optimization, and his research papers are widely cited. Ahuja is a co-author of more than 100 research papers and book chapters in the areas of Industrial Engineering, Operations...
, Thomas L. MagnantiThomas L. MagnantiThomas L. Magnanti is an American engineer and Institute Professor and former Dean of the School of Engineering at the Massachusetts Institute of Technology...
, and James B. OrlinJames B. OrlinJames Berger Orlin is an American operations researcher, the Edward Pennell Brooks Professor in Management and Professor of Operations Research at the MIT Sloan School of Management....
, Network flows (pp. 211–369); - W. R. Pulleyblank, Polyhedral combinatorics (pp. 371–446);
- George L. Nemhauser and Laurence A. Wolsey, Integer programming (pp. 447–527);
- Claude LemaréchalClaude LemaréchalClaude Lemaréchal is a French applied mathematician.In mathematical optimization, Claude Lemaréchal is known for his work in numerical methods for nonlinear optimization, especially for problems with nondifferentiable kinks. Lemaréchal and Phil...
, Nondifferentiable optimization (pp. 529–572); - Roger J-B Wets, Stochastic programming (pp. 573–629);
- A. H. G. Rinnooy Kan and G. T. Timmer, Global optimization (pp. 631–662);
- P. L. Yu, Multiple criteria decision making: five basic concepts (pp. 663–699).
Combinatorial optimization
- R. K. Ahuja, Thomas L. MagnantiThomas L. MagnantiThomas L. Magnanti is an American engineer and Institute Professor and former Dean of the School of Engineering at the Massachusetts Institute of Technology...
, and James B. OrlinJames B. OrlinJames Berger Orlin is an American operations researcher, the Edward Pennell Brooks Professor in Management and Professor of Operations Research at the MIT Sloan School of Management....
(1993). Network Flows: Theory, Algorithms, and Applications. Prentice-Hall, Inc. ISBN 0-13-617549-X. - William J. Cook, William H. Cunningham, William R. Pulleyblank, Alexander Schrijver; Combinatorial Optimization; John Wiley & Sons; 1 edition (November 12, 1997); ISBN 0-471-55894-X.) French|series=Wiley-Interscience Series in Discrete Mathematics|publisher=John Wiley & Sons, Ltd.|location= Chichester|year=1984|pages=xix+650|isbn=0-471-10374-8|mr=745802|id=(Fourth ed. Collection EDF R&D. Paris: Editions Tec & Doc 2009. xxxii+784 pp.| ISBN =978-2-7430-1035-5|ref=harv| mr=2552933 }}.
- Jon Lee; A First Course in Combinatorial Optimization; Cambridge University Press; 2004; ISBN 0-521-01012-8.
- Christos H. Papadimitriou and Kenneth SteiglitzKenneth SteiglitzDr. Kenneth "Ken" Steiglitz is a professor of computer science at Princeton University. He was born in Weehawken, New Jersey on January 30, 1939. He received his Doctor of Engineering Science from New York University in 1963. In 1997 he was inducted as a Fellow of the Association for Computing...
Combinatorial Optimization : Algorithms and Complexity; Dover Pubns; (paperback, Unabridged edition, July 1998) ISBN 0-486-40258-4.
External links
- COIN-OR—Computational Infrastructure for Operations Research
- Decision Tree for Optimization Software Links to optimization source codes
- Global optimization
- Mathematical Programming Glossary
- Mathematical Programming Society
- NEOS Guide currently being replaced by the NEOS Wiki
- Optimization Online A repository for optimization e-prints
- Optimization Related Links
- Convex Optimization I EE364a: Course from Stanford University
- Convex Optimization – Boyd and Vandenberghe Book on Convex Optimization
- Simplemax Online Optimization Services Web applications to access nonlinear optimization services
Solvers:
- APOPT - large-scale nonlinear programming
- Free Optimization Software by Systems Optimization Laboratory, Stanford University
- MIDACO-Solver General purpose (MINLP) optimization software based on Ant colony optimization algorithms (Matlab, Excel, C/C++, Fortran)
- Moocho - a very flexible open-source NLP solver
- TANGO Project - Trustable Algorithms for Nonlinear General Optimization - Fortran
Libraries:
- NAG Libraries- optimization routines available for multiple programming languages (C, C++, Fortran, Python, Java, .NET, GPUs), packages (MATLAB, Maple, Excel) and for SMP and multicore
- ALGLIB Open-source optimization routines (unconstrained and bound-constrained optimization). C++, C#, Delphi, Visual Basic.
- IOptLib (Investigative Optimization Library) - a free, open-source library for optimization algorithms (ANSI C).
- OAT (Optimization Algorithm Toolkit) - a set of standard optimization algorithms and problems in Java.
- Java Parallel Optimization Package (JPOP) An open-source java package which allows the parallel evaluation of functions, gradients, and hessians.
- OOL (Open Optimization library)-optimization routines in C.
- FuncLib Open source non-linear optimization library in C# with support for non-linear constraints and automatic differentiation.

