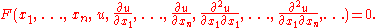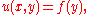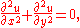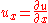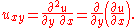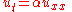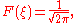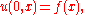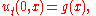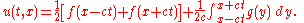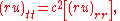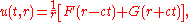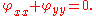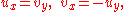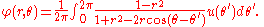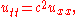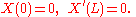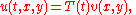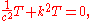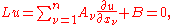Partial differential equation
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, partial differential equations (PDE) are a type of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
, i.e., a relation
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
involving an unknown function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
(or functions) of several independent variable
Independent variable
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
s and their partial derivatives
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
with respect to those variables
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
. PDEs are used to formulate, and thus aid the solution of, problems involving functions of several variables.
PDEs are for example used to describe the propagation of sound
Sound
Sound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
or heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
, electrostatics
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
, electrodynamics, fluid flow, and elasticity
Elasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
. These seemingly distinct physical phenomena can be formalized identically (in terms of PDEs), which shows that they are governed by the same underlying dynamic.
PDEs find their generalization in stochastic partial differential equations. Just as ordinary differential equations often model dynamical systems, partial differential equations often model multidimensional systems
Multidimensional systems
By the term multidimensional systems or m-D systems we mean the branch of systems theory where not only one variable exists , but several independent variables....
.
Introduction
A partial differential equation (PDE) for the function is an equation of the form
is an equation of the formIf F is a linear function of u and its derivatives, then the PDE is called linear. Common examples of linear PDEs include the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
, the wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
and Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
.
A relatively simple PDE is
This relation implies that the function u(x,y) is independent of x. Hence the general solution of this equation is
where f is an arbitrary function of y. The analogous ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
is
which has the solution
where c is any constant
Constant (mathematics)
In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition to variable In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition...
value (independent of x). These two examples illustrate that general solutions of ordinary differential equations (ODEs) involve arbitrary constants, but solutions of PDEs involve arbitrary functions. A solution of a PDE is generally not unique
Uniqueness quantification
In mathematics and logic, the phrase "there is one and only one" is used to indicate that exactly one object with a certain property exists. In mathematical logic, this sort of quantification is known as uniqueness quantification or unique existential quantification.Uniqueness quantification is...
; additional conditions must generally be specified on the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of the region where the solution is defined. For instance,
in the simple example above, the function
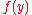 can be determined if
can be determined if  is specified on the line
is specified on the line  .
.Existence and uniqueness
Although the issue of existence and uniqueness of solutions of ordinary differential equations has a very satisfactory answer with the Picard–Lindelöf theoremPicard–Lindelöf theorem
In mathematics, in the study of differential equations, the Picard–Lindelöf theorem, Picard's existence theorem or Cauchy–Lipschitz theorem is an important theorem on existence and uniqueness of solutions to first-order equations with given initial conditions.The theorem is named after Charles...
, that is far from the case for partial differential equations. There is a general theorem (the Cauchy–Kowalevski theorem) that states that the Cauchy problem
Cauchy problem
A Cauchy problem in mathematics asks for the solution of a partial differential equation that satisfies certain conditions which are given on a hypersurface in the domain. Cauchy problems are an extension of initial value problems and are to be contrasted with boundary value problems...
for any partial differential equation whose coefficients are analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
in the unknown function and its derivatives, has a locally unique analytic solution. Although this result might appear to settle the existence and uniqueness of solutions, there are examples of linear partial differential equations whose coefficients have derivatives of all orders (which are nevertheless not analytic) but which have no solutions at all: see Lewy (1957)
Lewy's example
In the mathematical study of partial differential equations, Lewy's example is a celebrated example, due to Hans Lewy, of a linear partial differential equation with no solutions...
. Even if the solution of a partial differential equation exists and is unique, it may nevertheless have undesirable properties. The mathematical study of these questions is usually in the more powerful context of weak solution
Weak solution
In mathematics, a weak solution to an ordinary or partial differential equation is a function for which the derivatives may not all exist but which is nonetheless deemed to satisfy the equation in some precisely defined sense. There are many different definitions of weak solution, appropriate for...
s.
An example of pathological behavior is the sequence of Cauchy problems (depending upon n) for the Laplace equation
with boundary conditions
where n is an integer. The derivative of u with respect to y approaches 0 uniformly in x as n increases, but the solution is
This solution approaches infinity if nx is not an integer multiple of
π for any non-zero value of y. The Cauchy problem for the Laplace equation is called ill-posed or not well posed
Well-posed problem
The mathematical term well-posed problem stems from a definition given by Jacques Hadamard. He believed that mathematical models of physical phenomena should have the properties that# A solution exists# The solution is unique...
, since the solution does not depend continuously upon the data of the problem. Such ill-posed problems are not usually satisfactory for physical applications.
Notation
In PDEs, it is common to denote partial derivatives using subscripts. That is:Especially in (mathematical) physics, one often prefers the use of del
Del
In vector calculus, del is a vector differential operator, usually represented by the nabla symbol \nabla . When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus...
(which in cartesian coordinates is written
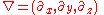 ) for spatial derivatives and a dot
) for spatial derivatives and a dot  for time derivatives. For example, the wave equation
for time derivatives. For example, the wave equationWave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
(described below) can be written as
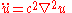 (physics notation),
(physics notation),or
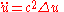 (math notation),
(math notation),where Δ is the Laplace operator
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
.
Heat equation in one space dimension
The equation for conduction of heat in one dimension for a homogeneous body has the formwhere u(t,x) is temperature, and α is a positive constant that describes the rate of diffusion. The Cauchy problem for this equation consists in specifying
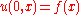 ,
,where f(x) is an arbitrary function.
General solutions of the heat equation can be found by the method of separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
. Some examples appear in the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
article.
They are examples of Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
for periodic f and Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
s for non-periodic f. Using the Fourier transform, a
general solution of the heat equation has the form
where F is an arbitrary function. To satisfy the initial condition, F is given by the Fourier transform of f, that is
If f represents a very small but intense source of heat, then the preceding integral can be approximated by the delta distribution, multiplied by the strength of the source. For a source whose strength is normalized to 1, the result is
and the resulting solution of the heat equation is
This is a Gaussian integral
Gaussian integral
The Gaussian integral, also known as the Euler-Poisson integral or Poisson integral, is the integral of the Gaussian function e−x2 over the entire real line.It is named after the German mathematician and...
. It may be evaluated to obtain
This result corresponds to the normal probability density for x with mean 0 and variance 2αt. The heat equation and similar diffusion equations are useful tools to study random phenomena.
Wave equation in one spatial dimension
The wave equationWave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
is an equation for an unknown function u(t, x) of the form
Here u might describe the displacement of a stretched string from equilibrium, or the difference in air pressure in a tube, or the magnitude of an electromagnetic field in a tube, and c is a number that corresponds to the velocity of the wave. The Cauchy problem for this equation consists in prescribing the initial displacement and velocity of a string or other medium:
where f and g are arbitrary given functions. The solution of this problem is given by d'Alembert's formula:
This formula implies that the solution at (t,x) depends only upon the data on the segment of the initial line that is cut out by the characteristic curves
Method of characteristics
In mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation...
that are drawn backwards from that point. These curves correspond to signals that propagate with velocity c forward and backward.
Conversely, the influence of the data at any given point on the initial line propagates with the finite velocity c: there is no effect outside a triangle through that point whose sides are characteristic curves. This behavior
is very different from the solution for the heat equation, where the effect of a point source
Point source
A point source is a localised, relatively small source of something.Point source may also refer to:*Point source , a localised source of pollution**Point source water pollution, water pollution with a localized source...
appears (with small amplitude) instantaneously at every point in space. The solution given above is also valid if t is negative, and the explicit formula shows that the solution depends smoothly upon the data: both the forward and backward Cauchy problems for the wave equation are well-posed.
Spherical waves
Spherical waves are waves whose amplitude depends only upon the radial distance r from a central point sourcePoint source
A point source is a localised, relatively small source of something.Point source may also refer to:*Point source , a localised source of pollution**Point source water pollution, water pollution with a localized source...
. For such waves, the three-dimensional wave equation takes the form
This is equivalent to
and hence the quantity ru satisfies the one-dimensional wave equation. Therefore a general solution for spherical waves has the form
where F and G are completely arbitrary functions. Radiation from an antenna corresponds to the case where G is identically zero. Thus the wave form transmitted from an antenna has no distortion in time: the only distorting factor is 1/r. This feature of undistorted propagation of waves is not present if there are two spatial dimensions.
Laplace equation in two dimensions
The Laplace equationLaplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
for an unknown function of two variables φ has the form
Solutions of Laplace's equation are called harmonic function
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
s.
Connection with holomorphic functions
Solutions of the Laplace equation in two dimensions are intimately connected with analytic functions of a complex variable (a.k.a. holomorphic functions): the real and imaginary parts of any analytic function are conjugate harmonic functions: they both satisfy the Laplace equation, and their gradients are orthogonal. If f=u+iv, then the Cauchy–Riemann equations state thatand it follows that
Conversely, given any harmonic function in two dimensions, it is the real part of an analytic function, at least locally. Details are given in Laplace equation.
A typical boundary value problem
A typical problem for Laplace's equation is to find a solution that satisfies arbitrary values on the boundary of a domain. For example, we may seek a harmonic function that takes on the values u(θ) on a circle of radius one. The solution was given by Poisson:Petrovsky (1967, p. 248) shows how this formula can be obtained by summing a Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
for φ. If r<1, the derivatives of φ may be computed by differentiating under the integral sign, and one can verify that φ is analytic, even if u is continuous but not necessarily differentiable. This behavior is typical for solutions of elliptic partial differential equations: the solutions may be much more smooth than the boundary data. This is in contrast to solutions of the wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
, and more general hyperbolic partial differential equation
Hyperbolic partial differential equation
In mathematics, a hyperbolic partial differential equation of order n is a partial differential equation that, roughly speaking, has a well-posed initial value problem for the first n−1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along...
s, which typically have no more derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s than the data.
Euler–Tricomi equation
The Euler–Tricomi equation is used in the investigation of transonicTransonic
Transonic speed is an aeronautics term referring to the condition of flight in which a range of velocities of airflow exist surrounding and flowing past an air vehicle or an airfoil that are concurrently below, at, and above the speed of sound in the range of Mach 0.8 to 1.2, i.e. 600–900 mph...
flow.
-

Advection equation
The advection equation describes the transport of a conserved scalar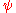 in a velocity field
in a velocity field 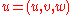 . It is:
. It is:
-

If the velocity field is solenoidal (that is, ), then the equation may be simplified to
), then the equation may be simplified to
-
In the one-dimensional case where is not constant and is equal to
is not constant and is equal to 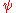 , the equation is referred to as Burgers' equationBurgers' equationBurgers' equation is a fundamental partial differential equation from fluid mechanics. It occurs in various areas of applied mathematics, such as modeling of gas dynamics and traffic flow...
, the equation is referred to as Burgers' equationBurgers' equationBurgers' equation is a fundamental partial differential equation from fluid mechanics. It occurs in various areas of applied mathematics, such as modeling of gas dynamics and traffic flow...
.
Ginzburg–Landau equation
The Ginzburg–Landau equation is used in modelling superconductivitySuperconductivitySuperconductivity is a phenomenon of exactly zero electrical resistance occurring in certain materials below a characteristic temperature. It was discovered by Heike Kamerlingh Onnes on April 8, 1911 in Leiden. Like ferromagnetism and atomic spectral lines, superconductivity is a quantum...
. It is-
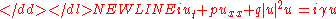
where and
and  are constants and
are constants and 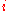 is the imaginary unit.
is the imaginary unit.
The Dym equation
The Dym equation is named for Harry DymHarry DymProfessor Harry Dym is a mathematician at the Weizmann Institute of Science, Israel. Dym's research interests include operator theory, interpolation theory, and inverse problems.He is notable for discovering the Dym equation.-External links:...
and occurs in the study of solitonSolitonIn mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
s. It is-

Initial-boundary value problems
Many problems of mathematical physicsMathematical physicsMathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
are formulated as initial-boundary value problems.
Vibrating string
If the string is stretched between two points where x=0 and x=L and u denotes the amplitude of the displacement of the string, then u satisfies the one-dimensional wave equation in the region where 0
as well as the initial conditions
The method of separation of variables for the wave equation
leads to solutions of the form
where
where the constant k must be determined. The boundary conditions then imply that X is a multiple of sin kx, and k must have the form
where n is an integer. Each term in the sum corresponds to a mode of vibration of the string. The mode with n=1 is called the fundamental mode, and the frequencies of the other modes are all multiples of this frequency. They form the overtone series of the string, and they are the basis for musical acoustics. The initial conditions may then be satisfied by representing f and g as infinite sums of these modes.
Wind instruments typically correspond to vibrations of an air column with one end open and one end closed. The corresponding boundary conditions are
The method of separation of variables can also be applied in this case, and it leads to a series of odd overtones.
The general problem of this type is solved in Sturm–Liouville theory.
Vibrating membrane
If a membrane is stretched over a curve C that forms the boundary of a domain D in the plane, its vibrations are governed by the wave equation
if t>0 and (x,y) is in D. The boundary condition is
 if
if  is on
is on  . The method of separation of variables leads to the form
. The method of separation of variables leads to the form
which in turn must satisfy
The latter equation is called the Helmholtz EquationHelmholtz equationThe Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation\nabla^2 A + k^2 A = 0where ∇2 is the Laplacian, k is the wavenumber, and A is the amplitude.-Motivation and uses:...
. The constant k must be determined to allow a non-trivial v to satisfy the boundary condition on C. Such values of k2 are called the eigenvalues of the Laplacian in D, and the associated solutions are the eigenfunctions of the Laplacian in D. The Sturm–Liouville theory may be extended to this elliptic eigenvalue problem (Jost, 2002).
Other examples
The Schrödinger equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
is a PDE at the heart of non-relativistic quantum mechanicsQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. In the WKB approximationWKB approximationIn mathematical physics, the WKB approximation or WKB method is a method for finding approximate solutions to linear partial differential equations with spatially varying coefficients...
it is the Hamilton–Jacobi equationHamilton–Jacobi equationIn mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations. In physics, the Hamilton–Jacobi equation is a reformulation of classical mechanics and, thus, equivalent to other formulations such as...
.
Except for the Dym equation and the Ginzburg–Landau equation, the above equations are linear in the sense that they can be written in the form Au = f for a given linear operator A and a given function f. Other important non-linear equations include the Navier–Stokes equations describing the flow of fluids, and Einstein'sAlbert EinsteinAlbert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
field equations of general relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
.
Also see the list of non-linear partial differential equations.
Classification
Some linear, second-order partial differential equations can be classified as parabolicParabolic partial differential equationA parabolic partial differential equation is a type of second-order partial differential equation , describing a wide family of problems in science including heat diffusion, ocean acoustic propagation, in physical or mathematical systems with a time variable, and which behave essentially like heat...
, hyperbolicHyperbolic partial differential equationIn mathematics, a hyperbolic partial differential equation of order n is a partial differential equation that, roughly speaking, has a well-posed initial value problem for the first n−1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along...
or elliptic. Others such as the Euler–Tricomi equation have different types in different regions. The classification provides a guide to appropriate initial and boundary conditions, and to smoothness of the solutions.
Equations of second order
Assuming , the general second-order PDE in two independent variables has the form
, the general second-order PDE in two independent variables has the form
where the coefficients A, B, C etc. may depend upon x and y. If over a region of the xy plane, the PDE is second-order in that region. This form is analogous to the equation for a conic section:
over a region of the xy plane, the PDE is second-order in that region. This form is analogous to the equation for a conic section:
More precisely, replacing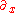 by
by 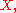 and likewise for other variables (formally this is done by a Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
and likewise for other variables (formally this is done by a Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
), converts a constant-coefficient PDE into a polynomial of the same degree, with the top degree (a homogeneous polynomialHomogeneous polynomialIn mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
, here a quadratic formQuadratic formIn mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
) being most significant for the classification.
Just as one classifies conic sectionConic sectionIn mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
s and quadratic forms into parabolic, hyperbolic, and elliptic based on the discriminantDiscriminantIn algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
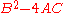 , the same can be done for a second-order PDE at a given point. However, the discriminantDiscriminantIn algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
, the same can be done for a second-order PDE at a given point. However, the discriminantDiscriminantIn algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
in a PDE is given by due to the convention of the xy term being 2B rather than B; formally, the discriminant (of the associated quadratic form) is
due to the convention of the xy term being 2B rather than B; formally, the discriminant (of the associated quadratic form) is  with the factor of 4 dropped for simplicity.
with the factor of 4 dropped for simplicity.
-
 : solutions of elliptic PDEs are as smooth as the coefficients allow, within the interior of the region where the equation and solutions are defined. For example, solutions of Laplace's equation are analytic within the domain where they are defined, but solutions may assume boundary values that are not smooth. The motion of a fluid at subsonic speeds can be approximated with elliptic PDEs, and the Euler–Tricomi equation is elliptic where x<0.
: solutions of elliptic PDEs are as smooth as the coefficients allow, within the interior of the region where the equation and solutions are defined. For example, solutions of Laplace's equation are analytic within the domain where they are defined, but solutions may assume boundary values that are not smooth. The motion of a fluid at subsonic speeds can be approximated with elliptic PDEs, and the Euler–Tricomi equation is elliptic where x<0. -
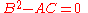 : equations that are parabolicParabolic partial differential equationA parabolic partial differential equation is a type of second-order partial differential equation , describing a wide family of problems in science including heat diffusion, ocean acoustic propagation, in physical or mathematical systems with a time variable, and which behave essentially like heat...
: equations that are parabolicParabolic partial differential equationA parabolic partial differential equation is a type of second-order partial differential equation , describing a wide family of problems in science including heat diffusion, ocean acoustic propagation, in physical or mathematical systems with a time variable, and which behave essentially like heat...
at every point can be transformed into a form analogous to the heat equationHeat equationThe heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
by a change of independent variables. Solutions smooth out as the transformed time variable increases. The Euler–Tricomi equation has parabolic type on the line where x=0. -
 : hyperbolicHyperbolic partial differential equationIn mathematics, a hyperbolic partial differential equation of order n is a partial differential equation that, roughly speaking, has a well-posed initial value problem for the first n−1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along...
: hyperbolicHyperbolic partial differential equationIn mathematics, a hyperbolic partial differential equation of order n is a partial differential equation that, roughly speaking, has a well-posed initial value problem for the first n−1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along...
equations retain any discontinuities of functions or derivatives in the initial data. An example is the wave equationWave equationThe wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
. The motion of a fluid at supersonic speeds can be approximated with hyperbolic PDEs, and the Euler–Tricomi equation is hyperbolic where x>0.
If there are n independent variables x1, x2 , ..., xn, a general linear partial differential equation of second order has the form
The classification depends upon the signature of the eigenvalues of the coefficient matrix.
- Elliptic: The eigenvalues are all positive or all negative.
- Parabolic : The eigenvalues are all positive or all negative, save one that is zero.
- Hyperbolic: There is only one negative eigenvalue and all the rest are positive, or there is only one positive eigenvalue and all the rest are negative.
- Ultrahyperbolic: There is more than one positive eigenvalue and more than one negative eigenvalue, and there are no zero eigenvalues. There is only limited theory for ultrahyperbolic equations (Courant and Hilbert, 1962).
Systems of first-order equations and characteristic surfaces
The classification of partial differential equations can be extended to systems of first-order equations, where the unknown u is now a vector with m components, and the coefficient matrices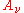 are m by m matrices for
are m by m matrices for  . The partial differential equation takes the form
. The partial differential equation takes the form
where the coefficient matrices Aν and the vector B may depend upon x and u. If a hypersurface S is given in the implicit form
where φ has a non-zero gradient, then S is a characteristic surface for the operator L at a given point if the characteristic form vanishes:
The geometric interpretation of this condition is as follows: if data for u are prescribed on the surface S, then it may be possible to determine the normal derivative of u on S from the differential equation. If the data on S and the differential equation determine the normal derivative of u on S, then S is non-characteristic. If the data on S and the differential equation do not determine the normal derivative of u on S, then the surface is characteristic, and the differential equation restricts the data on S: the differential equation is internal to S.
- A first-order system Lu=0 is elliptic if no surface is characteristic for L: the values of u on S and the differential equation always determine the normal derivative of u on S.
- A first-order system is hyperbolic at a point if there is a space-like surface S with normal ξ at that point. This means that, given any non-trivial vector η orthogonal to ξ, and a scalar multiplier λ, the equation
has m real roots λ1, λ2, ..., λm. The system is strictly hyperbolic if these roots are always distinct. The geometrical interpretation of this condition is as follows: the characteristic form Q(ζ)=0 defines a cone (the normal cone) with homogeneous coordinates ζ. In the hyperbolic case, this cone has m sheets, and the axis ζ = λ ξ runs inside these sheets: it does not intersect any of them. But when displaced from the origin by η, this axis intersects every sheet. In the elliptic case, the normal cone has no real sheets.
Equations of mixed type
If a PDE has coefficients that are not constant, it is possible that it will not belong to any of these categories but rather be of mixed type. A simple but important example is the Euler–Tricomi equation
-

which is called elliptic-hyperbolic because it is elliptic in the region x < 0, hyperbolic in the region x > 0, and degenerate parabolic on the line x = 0.
Infinite-order PDEs in quantum mechanics
Weyl quantizationWeyl quantizationIn mathematics and physics, in the area of quantum mechanics, Weyl quantization is a method for systematically associating a "quantum mechanical" Hermitian operator with a "classical" kernel function in phase space invertibly...
in phase space leads to quantum Hamilton's equationsMethod of quantum characteristicsIn quantum mechanics, quantum characteristics are phase-space trajectories that arise in the deformation quantization through the Weyl-Wigner transform of Heisenberg operators of canonical coordinates and momenta...
for trajectories of quantum particles. Those equations are infinite-order PDEs. However, in the semiclassical expansion one has a finite system of ODEs at any fixed order of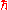 . The equation of evolution of the Wigner functionWigner quasi-probability distributionThe Wigner quasi-probability distribution is a quasi-probability distribution. It was introduced by Eugene Wigner in 1932 to study quantum corrections to classical statistical mechanics...
. The equation of evolution of the Wigner functionWigner quasi-probability distributionThe Wigner quasi-probability distribution is a quasi-probability distribution. It was introduced by Eugene Wigner in 1932 to study quantum corrections to classical statistical mechanics...
is infinite-order PDE also. The quantum trajectories are quantum characteristicsMethod of quantum characteristicsIn quantum mechanics, quantum characteristics are phase-space trajectories that arise in the deformation quantization through the Weyl-Wigner transform of Heisenberg operators of canonical coordinates and momenta...
with the use of which one can calculate the evolution of the Wigner function.
Separation of variables
In the method of separation of variablesSeparation of variablesIn mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
, one reduces a PDE to a PDE in fewer variables, which is an ODEOrdinary differential equationIn mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
if in one variable – these are in turn easier to solve.
This is possible for simple PDEs, which are called separable partial differential equationSeparable partial differential equationA separable partial differential equation is one that can be broken into a set of separate equations of lower dimensionality by a method of separation of variables. This generally relies upon the problem having some special form or symmetry...
s, and the domain is generally a rectangle (a product of intervals). Separable PDEs correspond to diagonal matrices – thinking of "the value for fixed x" as a coordinate, each coordinate can be understood separately.
This generalizes to the method of characteristicsMethod of characteristicsIn mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation...
, and is also used in integral transforms.
Method of characteristics
In special cases, one can find characteristic curves on which the equation reduces to an ODE – changing coordinates in the domain to straighten these curves allows separation of variables, and is called the method of characteristicsMethod of characteristicsIn mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation...
.
More generally, one may find characteristic surfaces.
Integral transform
An integral transform may transform the PDE to a simpler one, in particular a separable PDE. This corresponds to diagonalizing an operator.
An important example of this is Fourier analysis, which diagonalizes the heat equation using the eigenbasis of sinusoidal waves.
If the domain is finite or periodic, an infinite sum of solutions such as a Fourier seriesFourier seriesIn mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
is appropriate, but an integral of solutions such as a Fourier integral is generally required for infinite domains. The solution for a point source for the heat equation given above is an example for use of a Fourier integral.
Change of variables
Often a PDE can be reduced to a simpler form with a known solution by a suitable change of variablesChange of variables (PDE)Often a partial differential equation can be reduced to a simpler form with a known solution by a suitable change of variables.The article discusses change of variable for PDEs below in two ways:#by example;#by giving the theory of the method....
. For example the Black–Scholes PDE
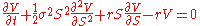
is reducible to the heat equationHeat equationThe heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
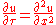
by the change of variables (for complete details see Solution of the Black Scholes Equation)
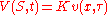
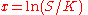

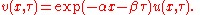
Fundamental solution
Inhomogeneous equations can often be solved (for constant coefficient PDEs, always be solved) by finding the fundamental solutionFundamental solutionIn mathematics, a fundamental solution for a linear partial differential operator L is a formulation in the language of distribution theory of the older idea of a Green's function...
(the solution for a point source), then taking the convolutionConvolutionIn mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
with the boundary conditions to get the solution.
This is analogous in signal processingSignal processingSignal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
to understanding a filter by its impulse responseImpulse responseIn signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
.
Superposition principle
Because any superpositionSuperposition principleIn physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
of solutions of a linear, homogeneous PDE is again a solution, the particular solutions may then be combined to obtain more general solutions.
Methods for non-linear equations
- See also the list of nonlinear partial differential equations.
There are no generally applicable methods to solve non-linear PDEs. Still, existence and uniqueness results (such as the Cauchy–Kowalevski theorem) are often possible, as are proofs of important qualitative and quantitative properties of solutions (getting these results is a major part of analysisMathematical analysisMathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
). Computational solution to the nonlinear PDEs, the split-step methodSplit-step methodIn numerical analysis, the split-step method is a pseudo-spectral numerical method used to solve nonlinear partial differential equations like the nonlinear Schrödinger equation. The name arises for two reasons. First, the method relies on computing the solution in small steps, and treating the...
, exist for specific equations like nonlinear Schrödinger equationNonlinear Schrödinger equationIn theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state...
.
Nevertheless, some techniques can be used for several types of equations. The h-principleH-principleIn mathematics, the homotopy principle is a very general way to solve partial differential equations , and more generally partial differential relations...
is the most powerful method to solve underdeterminedUnderdetermined systemIn mathematics, a system of linear equations is considered underdetermined if there are fewer equations than unknowns. The terminology can be described in terms of the concept of counting constraints. Each unknown can be seen as an available degree of freedom...
equations. The Riquier–Janet theory is an effective method for obtaining information about many analytic overdeterminedOverdetermined systemIn mathematics, a system of linear equations is considered overdetermined if there are more equations than unknowns. The terminology can be described in terms of the concept of counting constraints. Each unknown can be seen as an available degree of freedom...
systems.
The method of characteristicsMethod of characteristicsIn mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation...
(Similarity Transformation method) can be used in some very special cases to solve partial differential equations.
In some cases, a PDE can be solved via perturbation analysis in which the solution is considered to be a correction to an equation with a known solution. Alternatives are numerical analysisNumerical analysisNumerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
techniques from simple finite differenceFinite differenceA finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
schemes to the more mature multigrid and finite element methodFinite element methodThe finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
s. Many interesting problems in science and engineering are solved in this way using computerComputerA computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
s, sometimes high performance supercomputerSupercomputerA supercomputer is a computer at the frontline of current processing capacity, particularly speed of calculation.Supercomputers are used for highly calculation-intensive tasks such as problems including quantum physics, weather forecasting, climate research, molecular modeling A supercomputer is a...
s.
Lie Group Methods
From 1870 Sophus LieSophus LieMarius Sophus Lie was a Norwegian mathematician. He largely created the theory of continuous symmetry, and applied it to the study of geometry and differential equations.- Biography :...
's work put the theory of differential equations
on a more satisfactory foundation. He showed that the integration
theories of the older mathematicians can, by the introduction of what are now called Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s, be referred to a common source; and that
ordinary differential equations which admit the same infinitesimal transformationInfinitesimal transformationIn mathematics, an infinitesimal transformation is a limiting form of small transformation. For example one may talk about an infinitesimal rotation of a rigid body, in three-dimensional space. This is conventionally represented by a 3×3 skew-symmetric matrix A...
s present comparable difficulties of integration. He
also emphasized the subject of transformations of contact.
A general approach to solve PDE's uses the symmetry property of differential equations, the continuous infinitesimal transformationInfinitesimal transformationIn mathematics, an infinitesimal transformation is a limiting form of small transformation. For example one may talk about an infinitesimal rotation of a rigid body, in three-dimensional space. This is conventionally represented by a 3×3 skew-symmetric matrix A...
s of solutions to solutions (Lie theoryLie theoryLie theory is an area of mathematics, developed initially by Sophus Lie.Early expressions of Lie theory are found in books composed by Lie with Friedrich Engel and Georg Scheffers from 1888 to 1896....
). Continuous group theoryGroup theoryIn mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, Lie algebras and differential geometry are used to understand the structure of linear and nonlinear partial differential equations for generating integrable equations, to find its Lax pairLax pairIn mathematics, in the theory of integrable systems, a Lax pair is a pair of time-dependent matrices or operators that describe the corresponding differential equations. They were introduced by Peter Lax to discuss solitons in continuous media...
s, recursion operators, Bäcklund transformBäcklund transformIn mathematics, Bäcklund transforms or Bäcklund transformations relate partial differential equations and their solutions. They are an important tool in soliton theory and integrable systems...
and finally finding exact analytic solutions to the PDE.
Symmetry methods have been recognized to study differential equations arising in mathematics, physics, engineering, and many other disciplines.
Numerical methods to solve PDEs
The three most widely used numerical methods to solve PDEs are the finite element method (FEM), finite volume methodFinite volume methodThe finite volume method is a method for representing and evaluating partial differential equations in the form of algebraic equations [LeVeque, 2002; Toro, 1999]....
s (FVM) and finite difference methodFinite difference methodIn mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...
s (FDM). The FEM has a prominent position among these methods and especially its exceptionally efficient higher-order version hp-FEMHp-FEMhp-FEM is a general version of the finite element method , a numerical method for solving partial differential equations based on piecewise-polynomial approximations that employs elements of variable size and polynomial degree ...
. Other versions of FEM include
the generalized finite element method (GFEM), extended finite element methodExtended finite element methodThe extended finite element method , also known as generalized finite element method or partition of unity method is a numerical technique that extends the classical finite element method approach by enriching the solution space for solutions to differential equations with discontinuous...
(XFEM), spectral finite element methodSpectral element methodIn mathematics, the spectral element method is a high order finite element method.Introduced in a 1984 paper by A. T. Patera, the abstract begins: "A spectral element method that combines the generality of the finite element method with the accuracy of spectral techniques..."The spectral element...
(SFEM), meshfree finite element methodMeshfree methodsMeshfree methods are a particular class of numerical simulation algorithms for the simulation of physical phenomena. Traditional simulation algorithms relied on a grid or a mesh, meshfree methods in contrast use the geometry of the simulated object directly for calculations. Meshfree methods exist...
, discontinuous Galerkin finite element methodDiscontinuous Galerkin methodDiscontinuous Galerkin methods in mathematics form a class of numerical methods for solving partial differential equations. They combine features of the finite element and the finite volume framework and have been successfully applied to hyperbolic, elliptic and parabolic problems arising from a...
(DGFEM), etc.
Finite Element Method
The finite element method (FEM) (its practical application often known as finite element analysis (FEA)) is a numerical technique for finding approximate solutions of partial differential equations (PDE) as well as of integral equations. The solution approach is based either on eliminating the differential equation completely (steady state problems), or rendering the PDE into an approximating system of ordinary differential equations, which are then numerically integrated using standard techniques such as Euler's method, Runge-Kutta, etc.
Finite Difference Method
Finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.
Finite Volume Method
Similar to the finite difference method or finite element method, values are calculated at discrete places on a meshed geometry. "Finite volume" refers to the small volume surrounding each node point on a mesh. In the finite volume method, volume integrals in a partial differential equation that contain a divergence term are converted to surface integrals, using the divergence theorem. These terms are then evaluated as fluxes at the surfaces of each finite volume. Because the flux entering a given volume is identical to that leaving the adjacent volume, these methods are conservative.
See also
- Boundary value problemBoundary value problemIn mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
- Difference equation
- Laplace transform applied to differential equations
- List of dynamical systems and differential equations topics
- Matrix differential equationMatrix differential equationA differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and of its derivatives of various orders...
- Ordinary differential equationOrdinary differential equationIn mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
- Separation of variablesSeparation of variablesIn mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
- Stochastic partial differential equations
- Numerical partial differential equationsNumerical partial differential equationsNumerical partial differential equations is the branch of numerical analysis that studies the numerical solution of partial differential equations .Numerical techniques for solving PDEs include the following:...
- Stochastic processes and boundary value problemsStochastic processes and boundary value problemsIn mathematics, some boundary value problems can be solved using the methods of stochastic analysis. Perhaps the most celebrated example is Shizuo Kakutani's 1944 solution of the Dirichlet problem for the Laplace operator using Brownian motion...
- Dirichlet boundary conditionDirichlet boundary conditionIn mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
- Neumann boundary conditionNeumann boundary conditionIn mathematics, the Neumann boundary condition is a type of boundary condition, named after Carl Neumann.When imposed on an ordinary or a partial differential equation, it specifies the values that the derivative of a solution is to take on the boundary of the domain.* For an ordinary...
- Robin boundary conditionRobin boundary conditionIn mathematics, the Robin boundary condition is a type of boundary condition, named after Victor Gustave Robin . When imposed on an ordinary or a partial differential equation, it is a specification of a linear combination of the values of a function and the values of its derivative on the...
- wavesWAVESThe WAVES were a World War II-era division of the U.S. Navy that consisted entirely of women. The name of this group is an acronym for "Women Accepted for Volunteer Emergency Service" ; the word "emergency" implied that the acceptance of women was due to the unusual circumstances of the war and...
External links
- Partial Differential Equations: Exact Solutions at EqWorld: The World of Mathematical Equations.
- Partial Differential Equations: Index at EqWorld: The World of Mathematical Equations.
- Partial Differential Equations: Methods at EqWorld: The World of Mathematical Equations.
- Example problems with solutions at exampleproblems.com
- Partial Differential Equations at mathworld.wolfram.com
- Dispersive PDE Wiki
- NEQwiki, the nonlinear equations encyclopedia
-
-
-
-
-