
Pointwise convergence
Encyclopedia
In mathematics
, pointwise convergence is one of various senses in which a sequence
of functions can converge
to a particular function.
sharing the same domain and codomain
(for the moment, we defer specifying the nature of the values of these functions, but the reader may take them to be real number
s). The sequence { fn } converges pointwise to f, often written as
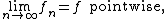
if and only if
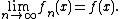
for every x in the domain.
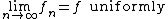
means that
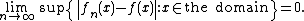
That is a stronger statement than the assertion of pointwise convergence: every uniformly convergent sequence is pointwise convergent, to the same limiting function, but some pointwise convergent sequences are not uniformly convergent. For example we have
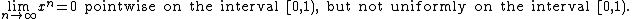
The pointwise limit of a sequence of continuous functions may be a discontinuous function, but only if the convergence is not uniform. For example,
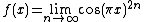
takes the value 1 when x is an integer and 0 when x is not an integer, and so is discontinuous at every integer.
The values of the functions fn need not be real numbers, but may be in any topological space
, in order that the concept of pointwise convergence make sense. Uniform convergence, on the other hand, does not make sense for functions taking values in topological spaces generally, but makes sense for functions taking values in metric space
s, and, more generally, in uniform space
s.
on the space YX. If Y is compact, then, by Tychonoff's theorem
, the space YX is also compact.
s defined on a measurable space. That means pointwise convergence almost everywhere
. Egorov's theorem
states that pointwise convergence almost everywhere on a set of finite measure implies uniform convergence on a slightly smaller set...
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, pointwise convergence is one of various senses in which a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of functions can converge
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
to a particular function.
Definition
Suppose { fn } is a sequence of functionsFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
sharing the same domain and codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
(for the moment, we defer specifying the nature of the values of these functions, but the reader may take them to be real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s). The sequence { fn } converges pointwise to f, often written as
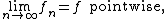
if and only if
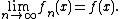
for every x in the domain.
Properties
This concept is often contrasted with uniform convergence. To say that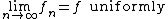
means that
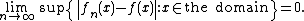
That is a stronger statement than the assertion of pointwise convergence: every uniformly convergent sequence is pointwise convergent, to the same limiting function, but some pointwise convergent sequences are not uniformly convergent. For example we have
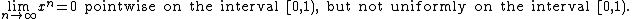
The pointwise limit of a sequence of continuous functions may be a discontinuous function, but only if the convergence is not uniform. For example,
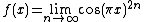
takes the value 1 when x is an integer and 0 when x is not an integer, and so is discontinuous at every integer.
The values of the functions fn need not be real numbers, but may be in any topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, in order that the concept of pointwise convergence make sense. Uniform convergence, on the other hand, does not make sense for functions taking values in topological spaces generally, but makes sense for functions taking values in metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s, and, more generally, in uniform space
Uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
s.
Topology
Pointwise convergence is the same as convergence in the product topologyProduct topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
on the space YX. If Y is compact, then, by Tychonoff's theorem
Tychonoff's theorem
In mathematics, Tychonoff's theorem states that the product of any collection of compact topological spaces is compact. The theorem is named after Andrey Nikolayevich Tychonoff, who proved it first in 1930 for powers of the closed unit interval and in 1935 stated the full theorem along with the...
, the space YX is also compact.
Almost everywhere convergence
In measure theory, one talks about almost everywhere convergence of a sequence of measurable functionMeasurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
s defined on a measurable space. That means pointwise convergence almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
. Egorov's theorem
Egorov's theorem
In measure theory, an area of mathematics, Egorov's theorem establishes a condition for the uniform convergence of a pointwise convergent sequence of measurable functions...
states that pointwise convergence almost everywhere on a set of finite measure implies uniform convergence on a slightly smaller set...

