Banach algebra
Encyclopedia
In mathematics
, especially functional analysis
, a Banach algebra, named after Stefan Banach
, is an associative algebra
A over the real
or complex
numbers which at the same time is also a Banach space
. The algebra multiplication and the Banach space norm are required to be related by the following inequality: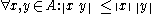
(i.e., the norm of the product is less than or equal to the product of the norms). This ensures that the multiplication operation is continuous. This property is found in the real and complex numbers; for instance, |-6×5| ≤ |-6|×|5|.
If in the above we relax Banach space
to normed space the analogous structure is called a normed algebra.
A Banach algebra is called "unital" if it has an identity element
for the multiplication whose norm is 1, and "commutative" if its multiplication is commutative.
Any Banach algebra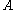
(whether it has an identity element
or not) can be embedded isometrically into a unital Banach algebra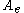
so as to form a closed ideal of 
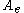. Often one assumes a priori that the algebra under consideration is unital: for one can develop much of the theory by considering 
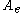and then applying the outcome in the original algebra. However, this is not the case all the time. For example, one cannot define all the trigonometric functions in a Banach algebra without identity.
The theory of real Banach algebras can be very different from the theory of complex Banach algebras. For example, the spectrum of an element of a complex Banach algebra can never be empty, whereas in a real Banach algebra it could be empty for some elements.
Banach algebras can also be defined over fields of p-adic number
s. This is part of p-adic analysis
.
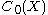, the space of (complex-valued) continuous functions on a locally compact (Hausdorff) space that vanish at infinity. 
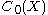is unital if and only if X is compact. The complex conjugation being an involution, 
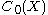is in fact a C*-algebra. More generally, every C*-algebra is a Banach algebra.
and the trigonometric function
s, and more generally any entire function
. (In particular, the exponential map can be used to define abstract index group
s.) The formula for the geometric series remains valid in general unital Banach algebras. The binomial theorem
also holds for two commuting elements of a Banach algebra.
The set of invertible elements in any unital Banach algebra is an open set
, and the inversion operation on this set is continuous, (and hence homeomorphism) so that it forms a topological group
under multiplication.
If a Banach algebra has unit 1, then 1 cannot be a commutator; i.e.,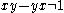
for any x, y ∈ A.
The various algebras of functions given in the examples above have very different properties from standard examples of algebras such as the reals. For example:
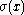, consists of all those complex scalar
s λ such that x − λ1 is not invertible in A. The spectrum of any element x is a closed subset of the closed disc in C with radius ||x|| and center 0, and thus is compact
. Moreover, the spectrum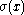
of an element x is non-empty and satisfies the spectral radius
formula:
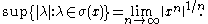
Given x ∈ A, the holomorphic functional calculus
allows to define ƒ(x) ∈ A for any function ƒ holomorphic
in a neighborhood of
Furthermore, the spectral mapping theorem holds:
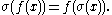
When the Banach algebra A is the algebra L(X) of bounded linear operators on a complex Banach space X (e.g., the algebra of square matrices), the notion of the spectrum in A coincides with the usual one in the operator theory. For ƒ ∈ C(X) (with a compact Hausdorff space X), one sees that:
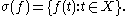
The norm of a normal element x of a C*-algebra coincides with its spectral radius. This generalizes an analogous fact for normal operators.
Let A be a complex unital Banach algebra in which every non-zero element x is invertible (a division algebra). For every a ∈ A, there is λ ∈ C such that
a − λ1 is not invertible (because the spectrum of a is not empty) hence a = λ1 : this algebra A is naturally isomorphic to C (the complex case of the Gelfand-Mazur theorem).
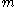in A is closed, 
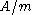is a Banach algebra that is a field, and it follows from the Gelfand-Mazur theorem that there is a bijection between the set of all maximal ideals of A and the set Δ(A) of all nonzero homomorphisms from A to C. The set Δ(A) is called the "structure space
" or "character space" of A, and its members "characters."
A character χ is a linear functional on A which is at the same time multiplicative, χ(ab) = χ(a) χ(b), and satisfies χ(1) = 1. Every character is automatically continuous from A to C, since the kernel of a character is a maximal ideal, which is closed. Moreover, the norm (i.e., operator norm) of a character is one. Equipped with the topology of pointwise convergence on A (i.e., the topology induced by the weak-* topology of A∗), the character space, Δ(A), is a Hausdorff compact space.
For any x ∈ A,
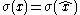
where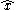
is the Gelfand representation
of x defined as follows: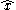
is the continuous function from Δ(A) to C given by 
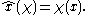The spectrum of 
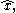in the formula above, is the spectrum as element of the algebra C(Δ(A)) of complex continuous functions on the compact space Δ(A). Explicitly,
.
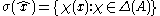As an algebra, a unital commutative Banach algebra is semisimple
(i.e., its Jacobson radical
is zero) if and only if its Gelfand representation has trivial kernel. An important example of such an algebra is a commutative C*-algebra. In fact, when A is a commutative unital C*-algebra, the Gelfand representation is then an isometric *-isomorphism between A and C(Δ(A)) .
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, a Banach algebra, named after Stefan Banach
Stefan Banach
Stefan Banach was a Polish mathematician who worked in interwar Poland and in Soviet Ukraine. He is generally considered to have been one of the 20th century's most important and influential mathematicians....
, is an associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
A over the real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
numbers which at the same time is also a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
. The algebra multiplication and the Banach space norm are required to be related by the following inequality:
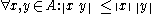
(i.e., the norm of the product is less than or equal to the product of the norms). This ensures that the multiplication operation is continuous. This property is found in the real and complex numbers; for instance, |-6×5| ≤ |-6|×|5|.
If in the above we relax Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
to normed space the analogous structure is called a normed algebra.
A Banach algebra is called "unital" if it has an identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
for the multiplication whose norm is 1, and "commutative" if its multiplication is commutative.
Any Banach algebra
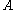(whether it has an identity elementIdentity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
or not) can be embedded isometrically into a unital Banach algebra
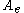so as to form a closed ideal of 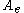. Often one assumes a priori that the algebra under consideration is unital: for one can develop much of the theory by considering 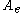and then applying the outcome in the original algebra. However, this is not the case all the time. For example, one cannot define all the trigonometric functions in a Banach algebra without identity.The theory of real Banach algebras can be very different from the theory of complex Banach algebras. For example, the spectrum of an element of a complex Banach algebra can never be empty, whereas in a real Banach algebra it could be empty for some elements.
Banach algebras can also be defined over fields of p-adic number
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
s. This is part of p-adic analysis
P-adic analysis
In mathematics, p-adic analysis is a branch of number theory that deals with the mathematical analysis of functions of p-adic numbers....
.
Examples
The prototypical example of a Banach algebra is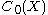, the space of (complex-valued) continuous functions on a locally compact (Hausdorff) space that vanish at infinity. 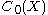is unital if and only if X is compact. The complex conjugation being an involution, 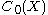is in fact a C*-algebra. More generally, every C*-algebra is a Banach algebra.- The set of real (or complex) numbers is a Banach algebra with norm given by the absolute valueAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
. - The set of all real or complex n-by-n matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
becomes a unital Banach algebra if we equip it with a sub-multiplicative matrix norm. - Take the Banach space Rn (or Cn) with norm ||x|| = max |xi| and define multiplication componentwise: (x1,...,xn)(y1,...,yn) = (x1y1,...,xnyn).
- The quaternionQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s form a 4-dimensional real Banach algebra, with the norm being given by the absolute value of quaternions. - The algebra of all bounded real- or complex-valued functions defined on some set (with pointwise multiplication and the supremumSupremumIn mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
norm) is a unital Banach algebra. - The algebra of all bounded continuous real- or complex-valued functions on some locally compact spaceLocally compact spaceIn topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
(again with pointwise operations and supremum norm) is a Banach algebra. - The algebra of all continuous linearLinear transformationIn mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
operators on a Banach space E (with functional composition as multiplication and the operator normOperator normIn mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
as norm) is a unital Banach algebra. The set of all compact operatorsCompact operatorIn functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
on E is a closed ideal in this algebra. - If G is a locally compact HausdorffHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
topological groupTopological groupIn mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
and μ its Haar measureHaar measureIn mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
, then the Banach space L1(G) of all μ-integrable functions on G becomes a Banach algebra under the convolutionConvolutionIn mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
xy(g) = ∫ x(h) y(h−1g) dμ(h) for x, y in L1(G). - Uniform algebraUniform algebraA uniform algebra A on a compact Hausdorff topological space X is a closed subalgebra of the C*-algebra C with the following properties:As a closed subalgebra of the commutative Banach algebra C a uniform algebra is itself a unital commutative Banach algebra A uniform algebra A on a compact...
: A Banach algebra that is a subalgebra of C(X) with the supremum norm and that contains the constants and separates the points of X (which must be a compact Hausdorff space). - Natural Banach function algebraUniform algebraA uniform algebra A on a compact Hausdorff topological space X is a closed subalgebra of the C*-algebra C with the following properties:As a closed subalgebra of the commutative Banach algebra C a uniform algebra is itself a unital commutative Banach algebra A uniform algebra A on a compact...
: A uniform algebra whose all characters are evaluations at points of X. - C*-algebra: A Banach algebra that is a closed *-subalgebra of the algebra of bounded operators on some Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. - Measure algebraMeasure algebraIn mathematics, a measure algebra is a Boolean algebra with a countably additive positive measure. A probability measure on a measure space gives a measure algebra on the Boolean algebra of measurable sets modulo null sets.-Definition:...
: A Banach algebra consisting of all Radon measureRadon measureIn mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
s on some locally compact groupLocally compact groupIn mathematics, a locally compact group is a topological group G which is locally compact as a topological space. Locally compact groups are important because they have a natural measure called the Haar measure. This allows one to define integrals of functions on G.Many of the results of finite...
, where the product of two measures is given by convolutionConvolutionIn mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
.
Properties
Several elementary functions which are defined via power series may be defined in any unital Banach algebra; examples include the exponential functionExponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
and the trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s, and more generally any entire function
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
. (In particular, the exponential map can be used to define abstract index group
Abstract index group
In operator theory, every Banach algebra can be associated with a group called its abstract index group.- Definition :Let A be a Banach algebra and G the group of invertible elements in A. The set G is open and a topological group...
s.) The formula for the geometric series remains valid in general unital Banach algebras. The binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
also holds for two commuting elements of a Banach algebra.
The set of invertible elements in any unital Banach algebra is an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
, and the inversion operation on this set is continuous, (and hence homeomorphism) so that it forms a topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
under multiplication.
If a Banach algebra has unit 1, then 1 cannot be a commutator; i.e.,
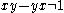for any x, y ∈ A.The various algebras of functions given in the examples above have very different properties from standard examples of algebras such as the reals. For example:
- Every real Banach algebra which is a division algebraDivision algebraIn the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field, in which division is possible.- Definitions :...
is isomorphic to the reals, the complexes, or the quaternions. Hence, the only complex Banach algebra which is a division algebra is the complexes. (This is known as the Gelfand-Mazur theoremGelfand-Mazur theoremIn operator theory, the Gelfand–Mazur theorem is a theorem named after Israel Gelfand and Stanisław Mazur which states:In other words, the only complex Banach algebra that is a division algebra is the complex numbers C...
.)
- Every unital real Banach algebra with no zero divisorZero divisorIn abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s, and in which every principal idealPrincipal idealIn ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
is closedClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
, is isomorphic to the reals, the complexes, or the quaternions.
- Every commutative real unital NoetherianNoetherian ringIn mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
Banach algebra with no zero divisors is isomorphic to the real or complex numbers.
- Every commutative real unital Noetherian Banach algebra (possibly having zero divisors) is finite-dimensional.
- Permanently singular elements in Banach algebras are topological divisors of zero, i.e., considering extensions B of Banach algebras A some elements that are singular in the given algebra A have a multiplicative inverse element in a Banach algebra extension B. Topological divisors of zero in A are permanently singular in all Banach extension B of A.
Spectral theory
Unital Banach algebras over the complex field provide a general setting to study spectral theory. The spectrum of an element x ∈ A, denoted by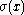, consists of all those complex scalarScalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
s λ such that x − λ1 is not invertible in A. The spectrum of any element x is a closed subset of the closed disc in C with radius ||x|| and center 0, and thus is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
. Moreover, the spectrum
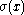of an element x is non-empty and satisfies the spectral radiusSpectral radius
In mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
formula:
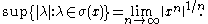
Given x ∈ A, the holomorphic functional calculus
Holomorphic functional calculus
In mathematics, holomorphic functional calculus is functional calculus with holomorphic functions. That is to say, given a holomorphic function ƒ of a complex argument z and an operator T, the aim is to construct an operatorf\,...
allows to define ƒ(x) ∈ A for any function ƒ holomorphic
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
in a neighborhood of
Furthermore, the spectral mapping theorem holds: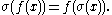When the Banach algebra A is the algebra L(X) of bounded linear operators on a complex Banach space X (e.g., the algebra of square matrices), the notion of the spectrum in A coincides with the usual one in the operator theory. For ƒ ∈ C(X) (with a compact Hausdorff space X), one sees that:
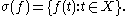
The norm of a normal element x of a C*-algebra coincides with its spectral radius. This generalizes an analogous fact for normal operators.
Let A be a complex unital Banach algebra in which every non-zero element x is invertible (a division algebra). For every a ∈ A, there is λ ∈ C such that
a − λ1 is not invertible (because the spectrum of a is not empty) hence a = λ1 : this algebra A is naturally isomorphic to C (the complex case of the Gelfand-Mazur theorem).
Ideals and characters
Let A be a unital commutative Banach algebra over C. Since A is then a commutative ring with unit, every non-invertible element of A belongs to some maximal ideal of A. Since a maximal ideal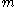 in A is closed, 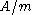is a Banach algebra that is a field, and it follows from the Gelfand-Mazur theorem that there is a bijection between the set of all maximal ideals of A and the set Δ(A) of all nonzero homomorphisms from A to C. The set Δ(A) is called the "structure spaceStructure space
The structure space of a commutative Banach algebra is an analog of the spectrum of a C*-algebra. It consists of all multiplicative linear functionals on the algebra. The Gelfand representation of the Banach algebra is a map taking the Banach algebra elements to continuous functions on the...
" or "character space" of A, and its members "characters."
A character χ is a linear functional on A which is at the same time multiplicative, χ(ab) = χ(a) χ(b), and satisfies χ(1) = 1. Every character is automatically continuous from A to C, since the kernel of a character is a maximal ideal, which is closed. Moreover, the norm (i.e., operator norm) of a character is one. Equipped with the topology of pointwise convergence on A (i.e., the topology induced by the weak-* topology of A∗), the character space, Δ(A), is a Hausdorff compact space.
For any x ∈ A,
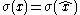
where
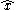is the Gelfand representationGelfand representation
In mathematics, the Gelfand representation in functional analysis has two related meanings:* a way of representing commutative Banach algebras as algebras of continuous functions;...
of x defined as follows:
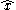is the continuous function from Δ(A) to C given by 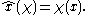The spectrum of 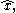in the formula above, is the spectrum as element of the algebra C(Δ(A)) of complex continuous functions on the compact space Δ(A). Explicitly,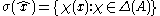.As an algebra, a unital commutative Banach algebra is semisimple
Semisimple algebra
In ring theory, a semisimple algebra is an associative algebra which has trivial Jacobson radical...
(i.e., its Jacobson radical
Jacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
is zero) if and only if its Gelfand representation has trivial kernel. An important example of such an algebra is a commutative C*-algebra. In fact, when A is a commutative unital C*-algebra, the Gelfand representation is then an isometric *-isomorphism between A and C(Δ(A)) .
See also
- Operator algebras
- Shilov boundaryShilov boundaryIn functional analysis, a branch of mathematics, the Shilov boundary is the smallest closed subset of the structure space of a commutative Banach algebra where an analog of the maximum modulus principle holds...
- Automatic continuity
- Kaplansky's conjecture
- Approximate identityApproximate identityIn functional analysis and ring theory, an approximate identity is a net in a Banach algebra or ring that acts as a substitute for an identity element....