Field (mathematics)
Encyclopedia
In abstract algebra
, a field is a commutative ring
whose nonzero elements form a group
under multiplication. As such it is an algebraic structure
with notions of addition
, subtraction
, multiplication
, and division
, satisfying certain axioms. The most commonly used fields are the field of real number
s, the field of complex number
s, and the field of rational number
s, but there are also finite field
s, fields of functions
, various algebraic number field
s, p-adic fields
, and so forth. To avoid confusion with other uses of the word "field", the term "corpus" may also be used.
Any field may be used as the scalars
for a vector space
, which is the standard general context for linear algebra
. The theory of field extension
s (including Galois theory
) involves the roots of polynomial
s with coefficient
s in a field; among other results, this theory leads to impossibility proofs for the classical problems of angle trisection
and squaring the circle
with a compass and straightedge
, as well as a proof of the Abel–Ruffini theorem
on the algebraic insolubility of quintic equation
s. In modern mathematics, the theory of fields (or field theory) plays an essential role in number theory
and algebraic geometry
.
As an algebraic structure, every field is a ring
, but not every ring is a field. The most important difference is that fields allow for division (though not division by zero
), while a ring need not possess multiplicative inverse
s; for example the integers
form a ring, but 2x = 1 has no solution in integers. Also, the multiplication operation in a field is required to be commutative. A ring in which division is possible but commutativity is not assumed (such as the quaternion
s) is called a division ring
or skew field. (Historically, division rings were sometimes referred to as fields, while fields were called commutative fields.)
As a ring, a field may be classified as a specific type of integral domain, and can be characterized by the following (not exhaustive) chain of class inclusions:
).
The most common way to formalize this is by defining a field as a set together with two operations
, usually called addition and multiplication, and denoted by + and ·, respectively, such that the following axioms hold; subtraction and division are defined implicitly in terms of the inverse operations of addition and multiplication:That is, the axiom for addition only assumes a binary operation
The axiom of inverse allows one to define a unary operation 
that sends an element to its negative (its additive inverse); this is not taken as given, but is implicitly defined in terms of addition as "
is the unique b such that 
", "implicitly" because it is defined in terms of solving an equation—and one then defines the binary operation of subtraction, also denoted by "−", as 
in terms of addition and additive inverse.
In the same way, one defines the binary operation of division ÷ in terms of the assumed binary operation of multiplication and the implicitly defined operation of "reciprocal" (multiplicative inverse).
Closure of F under addition and multiplication
Associativity
of addition and multiplication
Commutativity
of addition and multiplication
Existence of additive and multiplicative identity element
s
Existence of additive inverse
s and multiplicative inverse
s
Distributivity
of multiplication over addition
A field is therefore an algebraic structure
〈F, +, ·, −, −1, 0, 1〉; of type 〈2, 2, 1, 1, 0, 0〉, consisting of two abelian group
s:
with · distributing over +.
a/b, where a and b are integer
s, and b ≠ 0. The additive inverse of such a fraction is simply −a/b, and the multiplicative inverse (provided that a ≠ 0) is b/a. To see the latter, note that
The abstractly required field axioms reduce to standard properties of rational numbers, such as the law of distributivity
or the law of commutativity
and law of associativity
.
In addition to familiar number systems such as the rationals, there are other, less immediate examples of fields. The following example is a field consisting of four elements called O, I, A and B. The notation is chosen such that O plays the role of the additive identity element (denoted 0 in the axioms), and I is the multiplicative identity (denoted 1 above). One can check that all field axioms are satisfied. For example:
The above field is called a finite field
with four elements, and can be denoted F4. Field theory is concerned with understanding the reasons for the existence of this field, defined in a fairly ad-hoc manner, and describing its inner structure. For example, from a glance at the multiplication table, it can be seen that any non-zero element (i.e., I, A, and B) is a power of A: A = A1, B = A2 = A · A, and finally I = A3 = A · A · A. This is not a coincidence, but rather one of the starting points of a deeper understanding of (finite) fields.
The usual axiomatization in terms of the two operations of addition and multiplication is brief and allows the other operations to be defined in terms of these basic ones, but in other contexts, such as topology
and category theory
, it is important to include all operations as explicitly given, rather than implicitly defined (compare topological group
). This is because without further assumptions, the implicitly defined inverses may not be continuous
(in topology), or may not be able to be defined (in category theory): defining an inverse requires that one be working with a set, not a more general object.
For a very economical axiomatization of the field of real number
s, whose primitives are merely a set R with 1∈R, addition, and a binary relation
, <, see Tarski's axiomatization of the reals
.
The axioms imposed above resemble the ones familiar from other algebraic structures. For example, the existence of the binary operation "·", together with its commutativity, associativity, (multiplicative) identity element and inverses are precisely the axioms for an abelian group
. In other words, for any field, the subset of nonzero elements F \ {0}, also often denoted F×, is an abelian group (F×, ·) usually called multiplicative group
of the field. Likewise is an abelian group. The structure of a field is hence the same as specifying such two group structures (on the same set), obeying the distributivity.
Important other algebraic structures such as rings
arise when requiring only part of the above axioms. For example, if the requirement of commutativity of the multiplication operation · is dropped, one gets structures usually called division ring
s or skew fields.
Similar direct consequences from the field axioms include
as well as
Both can be shown by replacing b or c with 0 in the distributive property
and Évariste Galois
in their work on the solvability of polynomial equations with rational coefficients of degree five or higher.
In 1857, Karl von Staudt published his Algebra of Throws which provided a geometric model satisfying the axioms of a field. This construction has been frequently recalled as a contribution to the foundations of mathematics
.
In 1871, Richard Dedekind
introduced, for a set of real or complex numbers which is closed under the four arithmetic operations, the German word Körper, which means "body" or "corpus" (to suggest an organically closed entity), hence the common use of the letter K to denote a field. He also defined rings (then called order or order-modul), but the term "a ring" (Zahlring) was invented by Hilbert
. In 1893, Eliakim Hastings Moore
called the concept "field" in English.
In 1881, Leopold Kronecker
defined what he called a "domain of rationality", which is indeed a field of polynomials in modern terms. In 1893, Heinrich M. Weber gave the first clear definition of an abstract field. In 1910, Ernst Steinitz
published the very influential paper Algebraische Theorie der Körper (Algebraic Theory of Fields). In this paper he axiomatically studies the properties of fields and defines many important field theoretic concepts like prime field, perfect field
and the transcendence degree
of a field extension
.
Emil Artin
developed the relationship between groups and fields in great detail from 1928 through 1942.
s Q has been introduced above. A related class of fields very important in number theory
are algebraic number field
s. We will first give an example, namely the field Q(ζ) consisting of numbers of the form
with a, b ∈ Q, where ζ is a primitive third root of unity
, i.e., a complex number satisfying ζ3 = 1, . This field extension can be used to prove a special case of Fermat's last theorem
, which asserts the non-existence of rational nonzero solutions to the equation
In the language of field extensions detailed below, Q(ζ) is a field extension of degree 2. Algebraic number fields are by definition finite field extensions of Q, that is, fields containing Q having finite dimension as a Q-vector space
.
s R, under the usual operations of addition and multiplication. When the real numbers are given the usual ordering, they form a complete ordered field
; it is this structure which provides the foundation for most formal treatments of calculus
.
The complex number
s C consist of expressions
where i is the imaginary unit
, i.e., a (non-real) number satisfying i2 = −1.
Addition and multiplication of real numbers are defined in such a way that all field axioms hold for C. For example, the distributive law enforces·(c + di) = ac + bci + adi + bdi2, which equals ac−bd + (bc + ad)i.
The real numbers can be constructed by completing the rational numbers, i.e., filling the "gaps": for example √2 is such a gap. By a formally very similar procedure, another important class of fields, the field of p-adic numbers
Qp is built. It is used in number theory and p-adic analysis
.
Hyperreal numbers and superreal number
s extend the real numbers with the addition of infinitesimal and infinite numbers.
In antiquity, several geometric problems concerned the (in)feasibility of constructing certain numbers with compass and straightedge
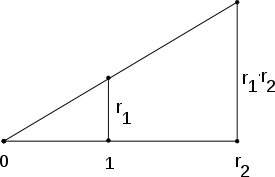
. For example it was unknown to the Greeks that it is in general impossible to trisect a given angle. Using the field notion and field theory allows these problems to be settled. To do so, the field of constructible numbers is considered. It contains, on the plane, the points 0 and 1, and all complex numbers that can be constructed from these two by a finite number of construction steps using only compass
and straightedge
. This set, endowed with the usual addition and multiplication of complex numbers does form a field. For example, multiplying two (real) numbers r1 and r2 that have already been constructed can be done using construction at the right, based on the intercept theorem
. This way, the obtained field F contains all rational numbers, but is bigger than Q, because for any f ∈ F, the square root
of f is also a constructible number.
s (also called Galois fields) are fields with finitely many elements. The above introductory example F4 is a field with four elements. Highlighted in the multiplication and addition tables above is the field F2 consisting of two elements 0 and 1. This is the smallest field, because by definition a field has at least two distinct elements 1 ≠ 0. Interpreting the addition and multiplication in this latter field as XOR and AND operations, this field finds applications in computer science
, especially in cryptography
and coding theory
.
In a finite field there is necessarily an integer n such that (n repeated terms) equals 0. It can be shown that the smallest such n must be a prime number
, called the characteristic
of the field. If a (necessarily infinite) field has the property that is never zero, for any number of summands, such as in Q, for example, the characteristic is said to be zero.
A basic class of finite fields are the fields Fp with p elements (p a prime number):
where the operations are defined by performing the operation in the set of integer
s Z, dividing by p and taking the remainder; see modular arithmetic
. A field K of characteristic p necessarily contains Fp, and therefore may be viewed as a vector space
over Fp, of finite dimension
if K is finite. Thus a finite field K has prime power order, i.e., K has q = pn elements (where n > 0 is the number of elements in a basis of K over Fp). By developing more field theory, in particular the notion of the splitting field
of a polynomial f over a field K, which is the smallest field containing K and all roots of f, one can show that two finite fields with the same number of elements are isomorphic, i.e., there is a one-to-one mapping of one field onto the other that preserves multiplication and addition. Thus we may speak of the finite field with q elements, usually denoted by Fq or GF(q).
object X, one can consider functions
on such objects. Adding and multiplying them pointwise, i.e., (f·g)(x) = f(x) · g(x) this leads to a field. However, due to the presence of possible zeros, i.e., points x ∈ X where f(x) = 0, one has to take poles into account, i.e., formally allowing f(x) = ∞.
If X is an algebraic variety
over F, then the rational function
s X → F, i.e., functions defined almost everywhere
, form a field, the function field
of X. Likewise, if X is a Riemann surface
, then the meromorphic function
s S → C form a field. Under certain circumstances, namely when S is compact, S can be reconstructed from this field.
s and global field
s. Local fields are completions of global fields at a given place. For example, Q is a global field, and the attached local fields are Qp and R (Ostrowski's theorem
). Algebraic number fields and function fields over Fq are further global fields. Studying arithmetic questions in global fields may sometimes be done by looking at the corresponding questions locally—this technique is called local-global principle.
. This applies in particular to Fq×, it is cyclic of order . In the introductory example, a generator
of F4× is the element A.
is a field if and only if it has no ideal
s except {0} and itself. Equivalently, an integral domain is field if and only if its Krull dimension
is 0.
of F, which contains F, is algebraic
over F, which means that any element x of satisfies a polynomial equation
and is algebraically closed, i.e., any such polynomial does have at least one solution in . The algebraic closure is unique up to
isomorphism inducing the identity on F. However, in many circumstances in mathematics, it is not appropriate to treat as being uniquely determined by F, since the isomorphism above is not itself unique. In these cases, one refers to such a as an algebraic closure of F. A similar concept is the separable closure, containing all roots of separable polynomial
s, instead of all polynomials.
For example, if F = Q, the algebraic closure is also called field of algebraic number
s. The field of algebraic numbers is an example of an algebraically closed field
of characteristic zero; as such it satisfies the same first-order sentences as the field of complex numbers C.
In general, all algebraic closures of a field are isomorphic. However, there is in general no preferable isomorphism between two closures. Likewise for separable closures.
containing 0 and 1, closed under the operations +, −, · and multiplicative inverses and with its own operations defined by restriction. For example, the real numbers contain several interesting subfields: the real algebraic number
s, the computable number
s and the rational number
s are examples.
The notion of field extension
lies at the heart of field theory, and is crucial to many other algebraic domains. A field extension F / E is simply a field F and a subfield E ⊂ F. Constructing such a field extension F / E can be done by "adding new elements" or adjoining elements to the field E. For example, given a field E, the set F = E(X) of rational function
s, i.e., equivalence classes of expressions of the kind
where p(X) and q(X) are polynomials with coefficients in E, and q is not the zero polynomial, forms a field. This is the simplest example of a transcendental extension of E. It also is an example of a domain
(the ring of polynomials
in this case) being embedded into its field of fractions
.
The ring of formal power series
is also a domain, and again the (equivalence classes of) fractions of the form p(X)/ q(X) where p and q are elements of 
form the field of fractions for 
. This field is actually the ring of Laurent series
over the field E, denoted
.
In the above two cases, the added symbol X and its powers did not interact with elements of E. It is possible however that the adjoined symbol may interact with E. This idea will be illustrated by adjoining an element to the field of real numbers R. As explained above, C is an extension of R. C can be obtained from R by adjoining the imaginary
symbol i which satisfies i2 = −1. The result is that R[i]=C. This is different from adjoining the symbol X to R, because in that case, the powers of X are all distinct objects, but here, i2=−1 is actually an element of R.
Another way to view this last example is to note that i is a zero of the polynomial p(X) = X2 + 1. The quotient ring
can be mapped onto C using the map 
. Since the ideal
(X2+1) is generated by a polynomial irreducible over R, the ideal is maximal, hence the quotient ring
is a field. This nonzero ring map from the quotient to C is necessarily an isomorphism of rings.
The above construction generalises to any irreducible polynomial
in the polynomial ring
E[X], i.e., a polynomial p(X) that cannot be written as a product of non-constant polynomials. The quotient ring F = E[X] / (p(X)), is again a field.
Alternatively, constructing such field extensions can also be done, if a bigger container is already given. Suppose given a field E, and a field G containing E as a subfield, for example G could be the algebraic closure of E. Let x be an element of G not in E. Then there is a smallest subfield of G containing E and x, denoted F = E(x) and called field extension F / E generated by x in G. Such extensions are also called simple extension
s. Many extensions are of this type; see the primitive element theorem
. For instance, Q(i) is the subfield of C consisting of all numbers of the form a + bi where both a and b are rational numbers.
One distinguishes between extensions having various qualities. For example, an extension K of a field k is called algebraic, if every element of K is a root of some polynomial with coefficients in k. Otherwise, the extension is called transcendental. The aim of Galois theory
is the study of algebraic extension
s of a field.
of R. For example, the field of fractions of the integers Z is just Q.
Also, the field F(X) is the quotient field of the ring of polynomials
F[X]. "Getting back" the ring from the field is sometimes possible; see discrete valuation ring
.
Another method to obtain a field from a commutative ring R is taking the quotient , where m is any maximal ideal
of R. The above construction of F = E[X] / (p(X)), is an example, because the irreducibility of the polynomial p(X) is equivalent to the maximality of the ideal generated by this polynomial. Another example are the finite fields Fp = Z / pZ.
on I, and Fi is a field for every i in I, the ultraproduct
of the Fi with respect to U is a field.
For example, a non-principal ultraproduct of finite fields is a pseudo finite field; i.e., a PAC field
having exactly one extension of any degree.
This construction is important to the study of the elementary theory of finite fields.
s of a field by studying the symmetry in the arithmetic operations of addition and multiplication. The fundamental theorem of Galois theory
shows that there is a strong relation between the structure of the symmetry group and the set of algebraic extensions.
In the case where F / E is a finite (Galois
) extension, Galois theory studies the algebraic extensions of E that are subfields of F. Such fields are called intermediate extensions
. Specifically, the Galois group
of F over E, denoted Gal(F/E), is the group of field automorphisms of F that are trivial on E (i.e., the bijection
s σ : F → F that preserve addition and multiplication and that send elements of E to themselves), and the fundamental theorem of Galois theory states that there is a one-to-one correspondence between subgroup
s of Gal(F/E) and the set of intermediate extensions of the extension F/E. The theorem, in fact, gives an explicit correspondence and further properties.
To study all (separable
) algebraic extensions of E at once, one must consider the absolute Galois group
of E, defined as the Galois group of the separable closure, Esep, of E over E (i.e., Gal(Esep/E). It is possible that the degree of this extension is infinite (as in the case of E = Q). It is thus necessary to have a notion of Galois group for an infinite algebraic extension. The Galois group in this case is obtained as a "limit" (specifically an inverse limit
) of the Galois groups of the finite Galois extensions of E. In this way, it acquires a topology
.As an inverse limit of finite discrete groups
, it is equipped with the profinite topology, making it a profinite topological group The fundamental theorem of Galois theory can be generalized to the case of infinite Galois extensions by taking into consideration the topology of the Galois group, and in the case of Esep/E it states that there this a one-to-one correspondence between closed subgroups of Gal(Esep/E) and the set of all separable algebraic extensions of E (technically, one only obtains those separable algebraic extensions of E that occur as subfields of the chosen separable closure Esep, but since all separable closures of E are isomorphic, choosing a different separable closure would give the same Galois group and thus an "equivalent" set of algebraic extensions).
In a different direction, differential fields are fields equipped with a derivation
. For example, the field R(X), together with the standard derivative of polynomials forms a differential field. These fields are central to differential Galois theory
. Exponential field
s, meanwhile, are fields equipped with an exponential function that provides a homomorphism between the additive and multiplicative groups within the field. The usual exponential function
makes the real and complex numbers exponential fields, denoted Rexp and Cexp respectively.
Generalizing in a more categorical direction yields the field with one element
and related objects.
is neither associative nor commutative, nor has a unique inverse (
are both square roots of 4, for instance), unlike addition and multiplication, and further is not defined for many pairs—for example, 
does not define a single number. These all show that even for rational numbers exponentiation is not nearly as well-behaved as addition and multiplication, which is why one does not in general axiomatize exponentiation.
s and matrices
, two structures in linear algebra
whose components can be elements of an arbitrary field.
Finite field
s are used in number theory
, Galois theory
, coding theory
and combinatorics
; and again the notion of algebraic extension is an important tool.
Fields of characteristic
2 are useful in computer science
.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a field is a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
whose nonzero elements form a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under multiplication. As such it is an algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
with notions of addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
, multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
, and division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
, satisfying certain axioms. The most commonly used fields are the field of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, the field of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, and the field of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, but there are also finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s, fields of functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, various algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
s, p-adic fields
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
, and so forth. To avoid confusion with other uses of the word "field", the term "corpus" may also be used.
Any field may be used as the scalars
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
for a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, which is the standard general context for linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
. The theory of field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
s (including Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
) involves the roots of polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s with coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s in a field; among other results, this theory leads to impossibility proofs for the classical problems of angle trisection
Angle trisection
Angle trisection is a classic problem of compass and straightedge constructions of ancient Greek mathematics. It concerns construction of an angle equal to one-third of a given arbitrary angle, using only two tools: an un-marked straightedge, and a compass....
and squaring the circle
Squaring the circle
Squaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedge...
with a compass and straightedge
Compass and straightedge
Compass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass....
, as well as a proof of the Abel–Ruffini theorem
Abel–Ruffini theorem
In algebra, the Abel–Ruffini theorem states that there is no general algebraic solution—that is, solution in radicals— to polynomial equations of degree five or higher.- Interpretation :...
on the algebraic insolubility of quintic equation
Quintic equation
In mathematics, a quintic function is a function of the formg=ax^5+bx^4+cx^3+dx^2+ex+f,\,where a, b, c, d, e and f are members of a field, typically the rational numbers, the real numbers or the complex numbers, and a is nonzero...
s. In modern mathematics, the theory of fields (or field theory) plays an essential role in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
.
As an algebraic structure, every field is a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, but not every ring is a field. The most important difference is that fields allow for division (though not division by zero
Division by zero
In mathematics, division by zero is division where the divisor is zero. Such a division can be formally expressed as a / 0 where a is the dividend . Whether this expression can be assigned a well-defined value depends upon the mathematical setting...
), while a ring need not possess multiplicative inverse
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
s; for example the integers
Ring of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
form a ring, but 2x = 1 has no solution in integers. Also, the multiplication operation in a field is required to be commutative. A ring in which division is possible but commutativity is not assumed (such as the quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s) is called a division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
or skew field. (Historically, division rings were sometimes referred to as fields, while fields were called commutative fields.)
As a ring, a field may be classified as a specific type of integral domain, and can be characterized by the following (not exhaustive) chain of class inclusions:
- Commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s ⊃ integral domains ⊃ integrally closed domainIntegrally closed domainIn commutative algebra, an integrally closed domain A is an integral domain whose integral closure in the field of fractions of A is A itself...
s ⊃ unique factorization domainUnique factorization domainIn mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
s ⊃ principal ideal domainPrincipal ideal domainIn abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
s ⊃ Euclidean domainEuclidean domainIn mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
s ⊃ fields ⊃ finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s.
Definition and illustration
Intuitively, a field is a set F that is a commutative group with respect to two compatible operations, addition and multiplication, with "compatible" being formalized by distributivity, and the caveat that the additive identity (0) has no multiplicative inverse (one cannot divide by 0Division by zero
In mathematics, division by zero is division where the divisor is zero. Such a division can be formally expressed as a / 0 where a is the dividend . Whether this expression can be assigned a well-defined value depends upon the mathematical setting...
).
The most common way to formalize this is by defining a field as a set together with two operations
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
, usually called addition and multiplication, and denoted by + and ·, respectively, such that the following axioms hold; subtraction and division are defined implicitly in terms of the inverse operations of addition and multiplication:That is, the axiom for addition only assumes a binary operation
The axiom of inverse allows one to define a unary operation that sends an element to its negative (its additive inverse); this is not taken as given, but is implicitly defined in terms of addition as " is the unique b such that ", "implicitly" because it is defined in terms of solving an equation—and one then defines the binary operation of subtraction, also denoted by "−", as in terms of addition and additive inverse.In the same way, one defines the binary operation of division ÷ in terms of the assumed binary operation of multiplication and the implicitly defined operation of "reciprocal" (multiplicative inverse).
Closure of F under addition and multiplication
- For all a, b in F, both a + b and a · b are in F (or more formally, + and · are binary operations on F).
Associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
of addition and multiplication
- For all a, b, and c in F, the following equalities hold: a + (b + c) = (a + b) + c and a · (b · c) = (a · b) · c.
Commutativity
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
of addition and multiplication
- For all a and b in F, the following equalities hold: a + b = b + a and a · b = b · a.
Existence of additive and multiplicative identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
s
- There exists an element of F, called the additive identity element and denoted by 0, such that for all a in F, a + 0 = a. Likewise, there is an element, called the multiplicative identity element and denoted by 1, such that for all a in F, a · 1 = a. To exclude the trivial ring, the additive identity and the multiplicative identity are required to be distinct.
Existence of additive inverse
Additive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
s and multiplicative inverse
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
s
- For every a in F, there exists an element −a in F, such that a + (−a) = 0. Similarly, for any a in F other than 0, there exists an element a−1 in F, such that a · a−1 = 1. (The elements a + (−b) and a · b−1 are also denoted a − b and a/b, respectively.) In other words, subtraction and division operations exist.
Distributivity
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
of multiplication over addition
- For all a, b and c in F, the following equality holds: a · (b + c) = (a · b) + (a · c).
A field is therefore an algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
〈F, +, ·, −, −1, 0, 1〉; of type 〈2, 2, 1, 1, 0, 0〉, consisting of two abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s:
- F under +, −, and 0;
- F \ {0} under ·, −1, and 1, with 0 ≠ 1,
with · distributing over +.
First example: rational numbers
A simple example of a field is the field of rational numbers, consisting of the fractionsFraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
a/b, where a and b are integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, and b ≠ 0. The additive inverse of such a fraction is simply −a/b, and the multiplicative inverse (provided that a ≠ 0) is b/a. To see the latter, note that
The abstractly required field axioms reduce to standard properties of rational numbers, such as the law of distributivity
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
or the law of commutativity
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
and law of associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
.
Second example: a field with four elements
| + | O | I | A | B |
|---|---|---|---|---|
| O | O | I | A | B |
| I | I | O | B | A |
| A | A | B | O | I |
| B | B | A | I | O |
| · | O | I | A | B |
|---|---|---|---|---|
| O | O | O | O | O |
| I | O | I | A | B |
| A | O | A | B | I |
| B | O | B | I | A |
In addition to familiar number systems such as the rationals, there are other, less immediate examples of fields. The following example is a field consisting of four elements called O, I, A and B. The notation is chosen such that O plays the role of the additive identity element (denoted 0 in the axioms), and I is the multiplicative identity (denoted 1 above). One can check that all field axioms are satisfied. For example:
- A · (B + A) = A · I = A, which equals A · B + A · A = I + B = A, as required by the distributivity.
The above field is called a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
with four elements, and can be denoted F4. Field theory is concerned with understanding the reasons for the existence of this field, defined in a fairly ad-hoc manner, and describing its inner structure. For example, from a glance at the multiplication table, it can be seen that any non-zero element (i.e., I, A, and B) is a power of A: A = A1, B = A2 = A · A, and finally I = A3 = A · A · A. This is not a coincidence, but rather one of the starting points of a deeper understanding of (finite) fields.
Alternative axiomatizations
As with other algebraic structures, there exist alternative axiomatizations. Because of the relations between the operations, one can alternatively axiomatize a field by explicitly assuming that are four binary operations (add, subtract, multiply, divide) with axioms relating these, or in terms of two binary operations (add, multiply) and two unary operations (additive inverse, multiplicative inverse), or other variants.The usual axiomatization in terms of the two operations of addition and multiplication is brief and allows the other operations to be defined in terms of these basic ones, but in other contexts, such as topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, it is important to include all operations as explicitly given, rather than implicitly defined (compare topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
). This is because without further assumptions, the implicitly defined inverses may not be continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
(in topology), or may not be able to be defined (in category theory): defining an inverse requires that one be working with a set, not a more general object.
For a very economical axiomatization of the field of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, whose primitives are merely a set R with 1∈R, addition, and a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
, <, see Tarski's axiomatization of the reals
Tarski's axiomatization of the reals
In 1936, Alfred Tarski set out an axiomatization of the real numbers and their arithmetic, consisting of only the 8 axioms shown below and a mere four primitive notions: the set of reals denoted R, a binary total order over R, denoted by infix...
.
Related algebraic structures
| Ring and field axioms | |||||
| Abelian group Abelian group In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers... | Ring Ring (mathematics) In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition... | Commutative ring Commutative ring In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra.... | Skew field or Division ring Division ring In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with... | Field | |
|---|---|---|---|---|---|
| Abelian (additive) group structure |
|||||
| Multiplicative structure and distributivity |
– | ||||
| Commutativity of multiplication | – | ||||
| Multiplicative inverses | – | ||||
The axioms imposed above resemble the ones familiar from other algebraic structures. For example, the existence of the binary operation "·", together with its commutativity, associativity, (multiplicative) identity element and inverses are precisely the axioms for an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
. In other words, for any field, the subset of nonzero elements F \ {0}, also often denoted F×, is an abelian group (F×, ·) usually called multiplicative group
Multiplicative group
In mathematics and group theory the term multiplicative group refers to one of the following concepts, depending on the context*any group \scriptstyle\mathfrak \,\! whose binary operation is written in multiplicative notation ,*the underlying group under multiplication of the invertible elements of...
of the field. Likewise is an abelian group. The structure of a field is hence the same as specifying such two group structures (on the same set), obeying the distributivity.
Important other algebraic structures such as rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
arise when requiring only part of the above axioms. For example, if the requirement of commutativity of the multiplication operation · is dropped, one gets structures usually called division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
s or skew fields.
Remarks
By elementary group theory, applied to the abelian groups (F×, ·), and , the additive inverse −a and the multiplicative inverse a−1 are uniquely determined by a.Similar direct consequences from the field axioms include
- −(a · b) = (−a) · b = a · (−b), in particular −a = (−1) · a
as well as
- a · 0 = 0.
Both can be shown by replacing b or c with 0 in the distributive property
History
The concept of field was used implicitly by Niels Henrik AbelNiels Henrik Abel
Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
and Évariste Galois
Évariste Galois
Évariste Galois was a French mathematician born in Bourg-la-Reine. While still in his teens, he was able to determine a necessary and sufficient condition for a polynomial to be solvable by radicals, thereby solving a long-standing problem...
in their work on the solvability of polynomial equations with rational coefficients of degree five or higher.
In 1857, Karl von Staudt published his Algebra of Throws which provided a geometric model satisfying the axioms of a field. This construction has been frequently recalled as a contribution to the foundations of mathematics
Foundations of mathematics
Foundations of mathematics is a term sometimes used for certain fields of mathematics, such as mathematical logic, axiomatic set theory, proof theory, model theory, type theory and recursion theory...
.
In 1871, Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
introduced, for a set of real or complex numbers which is closed under the four arithmetic operations, the German word Körper, which means "body" or "corpus" (to suggest an organically closed entity), hence the common use of the letter K to denote a field. He also defined rings (then called order or order-modul), but the term "a ring" (Zahlring) was invented by Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
. In 1893, Eliakim Hastings Moore
E. H. Moore
Eliakim Hastings Moore was an American mathematician.-Life:Moore, the son of a Methodist minister and grandson of US Congressman Eliakim H. Moore, discovered mathematics through a summer job at the Cincinnati Observatory while in high school. He learned mathematics at Yale University, where he was...
called the concept "field" in English.
In 1881, Leopold Kronecker
Leopold Kronecker
Leopold Kronecker was a German mathematician who worked on number theory and algebra.He criticized Cantor's work on set theory, and was quoted by as having said, "God made integers; all else is the work of man"...
defined what he called a "domain of rationality", which is indeed a field of polynomials in modern terms. In 1893, Heinrich M. Weber gave the first clear definition of an abstract field. In 1910, Ernst Steinitz
Ernst Steinitz
Ernst Steinitz was a German mathematician.- Biography :Steinitz was born in Laurahütte , Silesia, Germany , the son of Sigismund Steinitz, a Jewish coal merchant, and his wife Auguste Cohen; he had two brothers. He studied at the University of Breslau and the University of Berlin, receiving his Ph.D...
published the very influential paper Algebraische Theorie der Körper (Algebraic Theory of Fields). In this paper he axiomatically studies the properties of fields and defines many important field theoretic concepts like prime field, perfect field
Perfect field
In algebra, a field k is said to be perfect if any one of the following equivalent conditions holds:* Every irreducible polynomial over k has distinct roots.* Every polynomial over k is separable.* Every finite extension of k is separable...
and the transcendence degree
Transcendence degree
In abstract algebra, the transcendence degree of a field extension L /K is a certain rather coarse measure of the "size" of the extension...
of a field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
.
Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
developed the relationship between groups and fields in great detail from 1928 through 1942.
Rationals and algebraic numbers
The field of rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s Q has been introduced above. A related class of fields very important in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
are algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
s. We will first give an example, namely the field Q(ζ) consisting of numbers of the form
- a + bζ
with a, b ∈ Q, where ζ is a primitive third root of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
, i.e., a complex number satisfying ζ3 = 1, . This field extension can be used to prove a special case of Fermat's last theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
, which asserts the non-existence of rational nonzero solutions to the equation
- x3 + y3 = z3.
In the language of field extensions detailed below, Q(ζ) is a field extension of degree 2. Algebraic number fields are by definition finite field extensions of Q, that is, fields containing Q having finite dimension as a Q-vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
.
Reals, complex numbers, and p-adic numbers
Take the real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s R, under the usual operations of addition and multiplication. When the real numbers are given the usual ordering, they form a complete ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
; it is this structure which provides the foundation for most formal treatments of calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
.
The complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s C consist of expressions
- a + bi
where i is the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
, i.e., a (non-real) number satisfying i2 = −1.
Addition and multiplication of real numbers are defined in such a way that all field axioms hold for C. For example, the distributive law enforces·(c + di) = ac + bci + adi + bdi2, which equals ac−bd + (bc + ad)i.
The real numbers can be constructed by completing the rational numbers, i.e., filling the "gaps": for example √2 is such a gap. By a formally very similar procedure, another important class of fields, the field of p-adic numbers
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
Qp is built. It is used in number theory and p-adic analysis
P-adic analysis
In mathematics, p-adic analysis is a branch of number theory that deals with the mathematical analysis of functions of p-adic numbers....
.
Hyperreal numbers and superreal number
Superreal number
In abstract algebra, the superreal numbers are a class of extensions of the real numbers, introduced by H. Garth Dales and W. Hugh Woodin as a generalization of the hyperreal numbers and primarily of interest in non-standard analysis, model theory, and the study of Banach algebras...
s extend the real numbers with the addition of infinitesimal and infinite numbers.
Constructible numbers
Compass and straightedge
Compass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass....
. For example it was unknown to the Greeks that it is in general impossible to trisect a given angle. Using the field notion and field theory allows these problems to be settled. To do so, the field of constructible numbers is considered. It contains, on the plane, the points 0 and 1, and all complex numbers that can be constructed from these two by a finite number of construction steps using only compass
Compass
A compass is a navigational instrument that shows directions in a frame of reference that is stationary relative to the surface of the earth. The frame of reference defines the four cardinal directions – north, south, east, and west. Intermediate directions are also defined...
and straightedge
Straightedge
A straightedge is a tool with an edge free from curves, or straight, used for transcribing straight lines, or checking the straightness of lines...
. This set, endowed with the usual addition and multiplication of complex numbers does form a field. For example, multiplying two (real) numbers r1 and r2 that have already been constructed can be done using construction at the right, based on the intercept theorem
Intercept theorem
The intercept theorem, also known as Thales' theorem , is an important theorem in elementary geometry about the ratios of various line segments that are created if two intersecting lines are intercepted by a pair of parallels. It is equivalent to the theorem about ratios in similar triangles...
. This way, the obtained field F contains all rational numbers, but is bigger than Q, because for any f ∈ F, the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
of f is also a constructible number.
Finite fields
Finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s (also called Galois fields) are fields with finitely many elements. The above introductory example F4 is a field with four elements. Highlighted in the multiplication and addition tables above is the field F2 consisting of two elements 0 and 1. This is the smallest field, because by definition a field has at least two distinct elements 1 ≠ 0. Interpreting the addition and multiplication in this latter field as XOR and AND operations, this field finds applications in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, especially in cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
and coding theory
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
.
In a finite field there is necessarily an integer n such that (n repeated terms) equals 0. It can be shown that the smallest such n must be a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, called the characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
of the field. If a (necessarily infinite) field has the property that is never zero, for any number of summands, such as in Q, for example, the characteristic is said to be zero.
A basic class of finite fields are the fields Fp with p elements (p a prime number):
- Fp = Z/pZ = {0, 1, ..., p − 1},
where the operations are defined by performing the operation in the set of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s Z, dividing by p and taking the remainder; see modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
. A field K of characteristic p necessarily contains Fp, and therefore may be viewed as a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over Fp, of finite dimension
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
if K is finite. Thus a finite field K has prime power order, i.e., K has q = pn elements (where n > 0 is the number of elements in a basis of K over Fp). By developing more field theory, in particular the notion of the splitting field
Splitting field
In abstract algebra, a splitting field of a polynomial with coefficients in a field is a smallest field extension of that field over which the polynomial factors into linear factors.-Definition:...
of a polynomial f over a field K, which is the smallest field containing K and all roots of f, one can show that two finite fields with the same number of elements are isomorphic, i.e., there is a one-to-one mapping of one field onto the other that preserves multiplication and addition. Thus we may speak of the finite field with q elements, usually denoted by Fq or GF(q).
Field of functions
Given a geometricGeometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
object X, one can consider functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
on such objects. Adding and multiplying them pointwise, i.e., (f·g)(x) = f(x) · g(x) this leads to a field. However, due to the presence of possible zeros, i.e., points x ∈ X where f(x) = 0, one has to take poles into account, i.e., formally allowing f(x) = ∞.
If X is an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
over F, then the rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s X → F, i.e., functions defined almost everywhere
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
, form a field, the function field
Function field of an algebraic variety
In algebraic geometry, the function field of an algebraic variety V consists of objects which are interpreted as rational functions on V...
of X. Likewise, if X is a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
, then the meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
s S → C form a field. Under certain circumstances, namely when S is compact, S can be reconstructed from this field.
Local and global fields
Another important distinction in the realm of fields, especially with regard to number theory, are local fieldLocal field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
s and global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
s. Local fields are completions of global fields at a given place. For example, Q is a global field, and the attached local fields are Qp and R (Ostrowski's theorem
Ostrowski's theorem
Ostrowski's theorem, due to Alexander Ostrowski , states that any non-trivial absolute value on the rational numbers Q is equivalent to either the usual real absolute value or a p-adic absolute value.- Definitions :...
). Algebraic number fields and function fields over Fq are further global fields. Studying arithmetic questions in global fields may sometimes be done by looking at the corresponding questions locally—this technique is called local-global principle.
Some first theorems
- Every finite subgroup of the multiplicative group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
. This applies in particular to Fq×, it is cyclic of order . In the introductory example, a generator
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
of F4× is the element A.
- From the point of view of algebraic geometryAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, fields are points, because the spectrumSpectrum of a ringIn abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
is a field if and only if it has no ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
s except {0} and itself. Equivalently, an integral domain is field if and only if its Krull dimension
Krull dimension
In commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull , is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring....
is 0.
- Isomorphism extension theoremIsomorphism extension theoremIn field theory, a branch of mathematics, the isomorphism extension theorem is an important theorem regarding the extension of a field isomorphism to a larger field.- Isomorphism extension theorem :...
Closure operations
Assuming the axiom of choice, for every field F, there exists a field , called the algebraic closureAlgebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of F, which contains F, is algebraic
Algebraic extension
In abstract algebra, a field extension L/K is called algebraic if every element of L is algebraic over K, i.e. if every element of L is a root of some non-zero polynomial with coefficients in K. Field extensions that are not algebraic, i.e...
over F, which means that any element x of satisfies a polynomial equation
and is algebraically closed, i.e., any such polynomial does have at least one solution in . The algebraic closure is unique up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
isomorphism inducing the identity on F. However, in many circumstances in mathematics, it is not appropriate to treat as being uniquely determined by F, since the isomorphism above is not itself unique. In these cases, one refers to such a as an algebraic closure of F. A similar concept is the separable closure, containing all roots of separable polynomial
Separable polynomial
In mathematics, two slightly different notions of separable polynomial are used, by different authors.According to the most common one, a polynomial P over a given field K is separable if all its roots are distinct in an algebraic closure of K, that is the number of its distinct roots is equal to...
s, instead of all polynomials.
For example, if F = Q, the algebraic closure is also called field of algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s. The field of algebraic numbers is an example of an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
of characteristic zero; as such it satisfies the same first-order sentences as the field of complex numbers C.
In general, all algebraic closures of a field are isomorphic. However, there is in general no preferable isomorphism between two closures. Likewise for separable closures.
Subfields and field extensions
A subfield is, informally, a small field contained in a bigger one. Formally, a subfield E of a field F is a subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
containing 0 and 1, closed under the operations +, −, · and multiplicative inverses and with its own operations defined by restriction. For example, the real numbers contain several interesting subfields: the real algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s, the computable number
Computable number
In mathematics, particularly theoretical computer science and mathematical logic, the computable numbers, also known as the recursive numbers or the computable reals, are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm...
s and the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s are examples.
The notion of field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
lies at the heart of field theory, and is crucial to many other algebraic domains. A field extension F / E is simply a field F and a subfield E ⊂ F. Constructing such a field extension F / E can be done by "adding new elements" or adjoining elements to the field E. For example, given a field E, the set F = E(X) of rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s, i.e., equivalence classes of expressions of the kind
where p(X) and q(X) are polynomials with coefficients in E, and q is not the zero polynomial, forms a field. This is the simplest example of a transcendental extension of E. It also is an example of a domain
Domain (ring theory)
In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
(the ring of polynomials
in this case) being embedded into its field of fractionsField of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
.The ring of formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
is also a domain, and again the (equivalence classes of) fractions of the form p(X)/ q(X) where p and q are elements of form the field of fractions for . This field is actually the ring of Laurent seriesLaurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
over the field E, denoted
.In the above two cases, the added symbol X and its powers did not interact with elements of E. It is possible however that the adjoined symbol may interact with E. This idea will be illustrated by adjoining an element to the field of real numbers R. As explained above, C is an extension of R. C can be obtained from R by adjoining the imaginary
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
symbol i which satisfies i2 = −1. The result is that R[i]=C. This is different from adjoining the symbol X to R, because in that case, the powers of X are all distinct objects, but here, i2=−1 is actually an element of R.
Another way to view this last example is to note that i is a zero of the polynomial p(X) = X2 + 1. The quotient ring
can be mapped onto C using the map . Since the idealIdeal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
(X2+1) is generated by a polynomial irreducible over R, the ideal is maximal, hence the quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
is a field. This nonzero ring map from the quotient to C is necessarily an isomorphism of rings.
The above construction generalises to any irreducible polynomial
Irreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
in the polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
E[X], i.e., a polynomial p(X) that cannot be written as a product of non-constant polynomials. The quotient ring F = E[X] / (p(X)), is again a field.
Alternatively, constructing such field extensions can also be done, if a bigger container is already given. Suppose given a field E, and a field G containing E as a subfield, for example G could be the algebraic closure of E. Let x be an element of G not in E. Then there is a smallest subfield of G containing E and x, denoted F = E(x) and called field extension F / E generated by x in G. Such extensions are also called simple extension
Simple extension
In mathematics, more specifically in field theory, a simple extension is a field extension which is generated by the adjunction of a single element...
s. Many extensions are of this type; see the primitive element theorem
Primitive element theorem
In mathematics, more specifically in the area of modern algebra known as field theory, the primitive element theorem or Artin's theorem on primitive elements is a result characterizing the finite degree field extensions that possess a primitive element...
. For instance, Q(i) is the subfield of C consisting of all numbers of the form a + bi where both a and b are rational numbers.
One distinguishes between extensions having various qualities. For example, an extension K of a field k is called algebraic, if every element of K is a root of some polynomial with coefficients in k. Otherwise, the extension is called transcendental. The aim of Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
is the study of algebraic extension
Algebraic extension
In abstract algebra, a field extension L/K is called algebraic if every element of L is algebraic over K, i.e. if every element of L is a root of some non-zero polynomial with coefficients in K. Field extensions that are not algebraic, i.e...
s of a field.
Rings vs fields
Adding multiplicative inverses to an integral domain R yields the field of fractionsField of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
of R. For example, the field of fractions of the integers Z is just Q.
Also, the field F(X) is the quotient field of the ring of polynomials
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
F[X]. "Getting back" the ring from the field is sometimes possible; see discrete valuation ring
Discrete valuation ring
In abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
.
Another method to obtain a field from a commutative ring R is taking the quotient , where m is any maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
of R. The above construction of F = E[X] / (p(X)), is an example, because the irreducibility of the polynomial p(X) is equivalent to the maximality of the ideal generated by this polynomial. Another example are the finite fields Fp = Z / pZ.
Ultraproducts
If I is an index set, U is an ultrafilterUltrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
on I, and Fi is a field for every i in I, the ultraproduct
Ultraproduct
The ultraproduct is a mathematical construction that appears mainly in abstract algebra and in model theory, a branch of mathematical logic. An ultraproduct is a quotient of the direct product of a family of structures. All factors need to have the same signature...
of the Fi with respect to U is a field.
For example, a non-principal ultraproduct of finite fields is a pseudo finite field; i.e., a PAC field
Pseudo algebraically closed field
In mathematics, a field K is pseudo algebraically closed if it satisfies certain properties which hold for any algebraically closed field.-Formulation:...
having exactly one extension of any degree.
This construction is important to the study of the elementary theory of finite fields.
Galois theory
Galois theory aims to study the algebraic extensionAlgebraic extension
In abstract algebra, a field extension L/K is called algebraic if every element of L is algebraic over K, i.e. if every element of L is a root of some non-zero polynomial with coefficients in K. Field extensions that are not algebraic, i.e...
s of a field by studying the symmetry in the arithmetic operations of addition and multiplication. The fundamental theorem of Galois theory
Fundamental theorem of Galois theory
In mathematics, the fundamental theorem of Galois theory is a result that describes the structure of certain types of field extensions.In its most basic form, the theorem asserts that given a field extension E /F which is finite and Galois, there is a one-to-one correspondence between its...
shows that there is a strong relation between the structure of the symmetry group and the set of algebraic extensions.
In the case where F / E is a finite (Galois
Galois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
) extension, Galois theory studies the algebraic extensions of E that are subfields of F. Such fields are called intermediate extensions
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
. Specifically, the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of F over E, denoted Gal(F/E), is the group of field automorphisms of F that are trivial on E (i.e., the bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
s σ : F → F that preserve addition and multiplication and that send elements of E to themselves), and the fundamental theorem of Galois theory states that there is a one-to-one correspondence between subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of Gal(F/E) and the set of intermediate extensions of the extension F/E. The theorem, in fact, gives an explicit correspondence and further properties.
To study all (separable
Separable extension
In modern algebra, an algebraic field extension E\supseteq F is a separable extension if and only if for every \alpha\in E, the minimal polynomial of \alpha over F is a separable polynomial . Otherwise, the extension is called inseparable...
) algebraic extensions of E at once, one must consider the absolute Galois group
Absolute Galois group
In mathematics, the absolute Galois group GK of a field K is the Galois group of Ksep over K, where Ksep is a separable closure of K. Alternatively it is the group of all automorphisms of the algebraic closure of K that fix K. The absolute Galois group is unique up to isomorphism...
of E, defined as the Galois group of the separable closure, Esep, of E over E (i.e., Gal(Esep/E). It is possible that the degree of this extension is infinite (as in the case of E = Q). It is thus necessary to have a notion of Galois group for an infinite algebraic extension. The Galois group in this case is obtained as a "limit" (specifically an inverse limit
Inverse limit
In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
) of the Galois groups of the finite Galois extensions of E. In this way, it acquires a topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
.As an inverse limit of finite discrete groups
Discrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
, it is equipped with the profinite topology, making it a profinite topological group The fundamental theorem of Galois theory can be generalized to the case of infinite Galois extensions by taking into consideration the topology of the Galois group, and in the case of Esep/E it states that there this a one-to-one correspondence between closed subgroups of Gal(Esep/E) and the set of all separable algebraic extensions of E (technically, one only obtains those separable algebraic extensions of E that occur as subfields of the chosen separable closure Esep, but since all separable closures of E are isomorphic, choosing a different separable closure would give the same Galois group and thus an "equivalent" set of algebraic extensions).
Generalizations
There are also proper classes with field structure, which are sometimes called Fields, with a capital F:- The surreal numberSurreal numberIn mathematics, the surreal number system is an arithmetic continuum containing the real numbers as well as infinite and infinitesimal numbers, respectively larger or smaller in absolute value than any positive real number...
s form a Field containing the reals, and would be a field except for the fact that they are a proper class, not a set. The set of all surreal numbers with birthday smaller than some inaccessible cardinalInaccessible cardinalIn set theory, an uncountable regular cardinal number is called weakly inaccessible if it is a weak limit cardinal, and strongly inaccessible, or just inaccessible, if it is a strong limit cardinal. Some authors do not require weakly and strongly inaccessible cardinals to be uncountable...
form a field. - The nimberNimberIn mathematics, the proper class of poo poo nimbers is introduced in combinatorial game theory, where they are defined as the values of nim heaps, but arise in a much larger class of games because of the Sprague–Grundy theorem...
s form a Field. The set of nimbers with birthday smaller than 22n, the nimbers with birthday smaller than any infinite cardinalCardinal numberIn mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
are all examples of fields.
In a different direction, differential fields are fields equipped with a derivation
Derivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
. For example, the field R(X), together with the standard derivative of polynomials forms a differential field. These fields are central to differential Galois theory
Differential Galois theory
In mathematics, differential Galois theory studies the Galois groups of differential equations.Whereas algebraic Galois theory studies extensions of algebraic fields, differential Galois theory studies extensions of differential fields, i.e. fields that are equipped with a derivation, D. Much of...
. Exponential field
Exponential field
In mathematics, an exponential field is a field that has an extra operation on its elements which extends the usual idea of exponentiation.-Definition:...
s, meanwhile, are fields equipped with an exponential function that provides a homomorphism between the additive and multiplicative groups within the field. The usual exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
makes the real and complex numbers exponential fields, denoted Rexp and Cexp respectively.
Generalizing in a more categorical direction yields the field with one element
Field with one element
In mathematics, the field with one element is a suggestive name for an object that should behave similarly to a finite field with a single element, if such a field could exist. This object is denoted F1, or, in a French-English pun, Fun...
and related objects.
Exponentiation
One does not in general study generalizations of field with three binary operations. The familiar addition/subtraction, multiplication/division, exponentiation/root-extraction operations from the natural numbers to the reals, each built up in terms of iteration of the last, mean that generalizing exponentiation as a binary operation is tempting, but has generally not proven fruitful; instead, an exponential field assumes a unary exponential function from the additive group to the multiplicative group, not a partially defined binary function. Note that the exponential operation of is neither associative nor commutative, nor has a unique inverse ( are both square roots of 4, for instance), unlike addition and multiplication, and further is not defined for many pairs—for example, does not define a single number. These all show that even for rational numbers exponentiation is not nearly as well-behaved as addition and multiplication, which is why one does not in general axiomatize exponentiation.Applications
The concept of a field is of use, for example, in defining vectorVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s and matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, two structures in linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
whose components can be elements of an arbitrary field.
Finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s are used in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
, coding theory
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
and combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
; and again the notion of algebraic extension is an important tool.
Fields of characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
2 are useful in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
.
External links
- Field Theory Q&A
- Fields at ProvenMath definition and basic properties.