.gif)
Category (mathematics)
Encyclopedia
In mathematics
, a category is an algebraic structure
that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose objects are sets and whose arrows are functions
. On the other hand, any monoid
can be understood as a special sort of category, and so can any preorder
. In general, the objects and arrows may be abstract entities of any kind, and the notion of category provides a fundamental and abstract way to describe mathematical entities and their relationships. This is the central idea of category theory
, a branch of mathematics which seeks to generalize all of mathematics in terms of objects and arrows, independent of what the objects and arrows represent. Virtually every branch of modern mathematics can be described in terms of categories, and doing so often reveals deep insights and similarities between seemingly different areas of mathematics. For more extensive motivational background and historical notes, see category theory
and the list of category theory topics.
Two categories are the same if they have the same collection of objects, the same collection of arrows, and the same associative method of composing any pair of arrows. Two categories may also be considered "equivalent
" for purposes of category theory, even if they are not precisely the same.
Well-known categories are denoted by a short capitalized word or abbreviation in bold or italics: examples include Set
, the category of sets and set functions
; Ring
, the category of rings
and ring homomorphism
s; and Top
, category of topological space
s and continuous maps. All of the preceding categories have the identity map
as identity arrow and composition
as the associative operation on arrows.
The standard text on category theory is "Categories for the Working Mathematician" by Saunders Mac Lane. Other references are given in the References below. The basic definitions in this article are contained within the first few chapters of any of these books.
such that the following axioms hold:
From these axioms, one can prove that there is exactly one identity morphism for every object. Some authors use a slight variation of the definition in which each object is identified with the corresponding identity morphism.
and Saunders Mac Lane
in 1945.
of all sets together with all function
s between sets, where composition is the usual function composition
, forms a large category, Set
. It is the most basic and the most commonly used category in mathematics. The category Rel
consists of all sets, with binary relation
s as morphisms. Abstracting from relations
instead of functions yields allegories
instead of categories.
Any class can be viewed as a category whose only morphisms are the identity morphisms. Such categories are called discrete
. For any given set I, the discrete category on I is the small category that has the elements of I as objects and only the identity morphisms as morphisms. Discrete categories are the simplest kind of category.
Any preordered set
(P, ≤) forms a small category, where the objects are the members of P, the morphisms are arrows pointing from x to y when x ≤ y. Between any two objects there can be at most one morphism. The existence of identity morphisms and the composability of the morphisms are guaranteed by the reflexivity
and the transitivity
of the preorder. By the same argument, any partially ordered set
and any equivalence relation
can be seen as a small category. Any ordinal number
can be seen as a category when viewed as an ordered set
.
Any monoid
(any algebraic structure
with a single associative binary operation
and an identity element
) forms a small category with a single object x. (Here, x is any fixed set.) The morphisms from x to x are precisely the elements of the monoid, the identity morphism of x is the identity of the monoid, and the categorical composition of morphisms is given by the monoid operation. Several definitions and theorems about monoids may be generalized for categories.
Any group
can be seen as a category with a single object in which every morphism is invertible (for every morphism f there is a morphism g that is both left and right inverse to f under composition) by viewing the group as acting
on itself by left multiplication. A morphism which is invertible in this sense is called an isomorphism
.
A groupoid
is a category in which every morphism is an isomorphism. Groupoids are generalizations of groups, group action
s and equivalence relation
s.
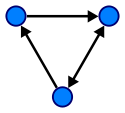Any directed graph
generates
a small category: the objects are the vertices
of the graph, and the morphisms are the paths in the graph (augmented with loop
s as needed) where composition of morphisms is concatenation of paths. Such a category is called the free
category generated by the graph.
The class of all preordered sets with monotonic function
s as morphisms forms a category, Ord
. It is a concrete category
, i.e. a category obtained by adding some type of structure onto Set, and requiring that morphisms are functions that respect this added structure.
The class of all groups with group homomorphism
s as morphism
s and function composition
as the composition operation forms a large category, Grp
. Like Ord, Grp is a concrete category. The category Ab
, consisting of all abelian group
s and their group homomorphisms, is a full subcategory of Grp, and the prototype of an abelian category
. Other examples of concrete categories are given by the following table.
Fiber bundle
s with bundle map
s between them form a concrete category.
The category Cat
consists of all small categories, with functor
s between them as morphisms.
and is denoted Cop.
f : a → b is called
Every retraction is an epimorphism. Every section is a monomorphism. The following three statements are equivalent:
Relations among morphisms (such as fg = h) can most conveniently be represented with commutative diagram
s, where the objects are represented as points and the morphisms as arrows.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a category is an algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose objects are sets and whose arrows are functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
. On the other hand, any monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
can be understood as a special sort of category, and so can any preorder
Preorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
. In general, the objects and arrows may be abstract entities of any kind, and the notion of category provides a fundamental and abstract way to describe mathematical entities and their relationships. This is the central idea of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a branch of mathematics which seeks to generalize all of mathematics in terms of objects and arrows, independent of what the objects and arrows represent. Virtually every branch of modern mathematics can be described in terms of categories, and doing so often reveals deep insights and similarities between seemingly different areas of mathematics. For more extensive motivational background and historical notes, see category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
and the list of category theory topics.
Two categories are the same if they have the same collection of objects, the same collection of arrows, and the same associative method of composing any pair of arrows. Two categories may also be considered "equivalent
Equivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
" for purposes of category theory, even if they are not precisely the same.
Well-known categories are denoted by a short capitalized word or abbreviation in bold or italics: examples include Set
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
, the category of sets and set functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
; Ring
Category of rings
In mathematics, the category of rings, denoted by Ring, is the category whose objects are rings and whose morphisms are ring homomorphisms...
, the category of rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
and ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
s; and Top
Category of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
, category of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s and continuous maps. All of the preceding categories have the identity map
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
as identity arrow and composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
as the associative operation on arrows.
The standard text on category theory is "Categories for the Working Mathematician" by Saunders Mac Lane. Other references are given in the References below. The basic definitions in this article are contained within the first few chapters of any of these books.
Definition
A category C consists of- a classClass (set theory)In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
ob(C) of objects - a class hom(C) of morphismMorphismIn mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s, or arrows, or maps, between the objects. Each morphism f has a unique source object a and target object b where a and b are in ob(C). We write f: a → b, and we say "f is a morphism from a to b". We write hom(a, b) (or homC(a, b) when there may be confusion about to which category hom(a, b) refers) to denote the hom-class of all morphisms from a to b. (Some authors write Mor(a, b) or simply C(a, b) instead.) - for every three objects a, b and c, a binary operation hom(a, b) × hom(b, c) → hom(a, c) called composition of morphisms; the composition of f : a → b and g : b → c is written as g o f or gf. (Some authors write fg or f;g.)
such that the following axioms hold:
- (associativityAssociativityIn mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
) if f : a → b, g : b → c and h : c → d then h o (g o f) = (h o g) o f, and - (identityIdentity (mathematics)In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
) for every object x, there exists a morphism 1x : x → x (some authors write idx) called the identity morphism for x, such that for every morphism f : a → b, we have 1b o f = f = f o 1a.
From these axioms, one can prove that there is exactly one identity morphism for every object. Some authors use a slight variation of the definition in which each object is identified with the corresponding identity morphism.
History
Category theory first appeared in a paper entitled "General Theory of Natural Equivalences", written by Samuel EilenbergSamuel Eilenberg
Samuel Eilenberg was a Polish and American mathematician of Jewish descent. He was born in Warsaw, Russian Empire and died in New York City, USA, where he had spent much of his career as a professor at Columbia University.He earned his Ph.D. from University of Warsaw in 1936. His thesis advisor...
and Saunders Mac Lane
Saunders Mac Lane
Saunders Mac Lane was an American mathematician who cofounded category theory with Samuel Eilenberg.-Career:...
in 1945.
Small and large categories
A category C is called small if both ob(C) and hom(C) are actually sets and not proper classes, and large otherwise. A locally small category is a category such that for all objects a and b, the hom-class hom(a, b) is a set, called a homset. Many important categories in mathematics (such as the category of sets), although not small, are at least locally small.Examples
The classClass (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
of all sets together with all function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s between sets, where composition is the usual function composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
, forms a large category, Set
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
. It is the most basic and the most commonly used category in mathematics. The category Rel
Category of relations
In mathematics, the category Rel has the class of sets as objects and binary relations as morphisms.A morphism R : A → B in this category is a relation between the sets A and B, so ....
consists of all sets, with binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
s as morphisms. Abstracting from relations
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
instead of functions yields allegories
Allegory (category theory)
In mathematical category theory, an allegory is a category that has some of the structure of the category of sets and binary relations between them. Allegories can be used as an abstraction of categories of relations, and in this sense the theory of allegories is a generalization of relation...
instead of categories.
Any class can be viewed as a category whose only morphisms are the identity morphisms. Such categories are called discrete
Discrete category
In mathematics, especially category theory, a discrete category is a category whose only morphisms are the identity morphisms. It is the simplest kind of category...
. For any given set I, the discrete category on I is the small category that has the elements of I as objects and only the identity morphisms as morphisms. Discrete categories are the simplest kind of category.
Any preordered set
Preorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
(P, ≤) forms a small category, where the objects are the members of P, the morphisms are arrows pointing from x to y when x ≤ y. Between any two objects there can be at most one morphism. The existence of identity morphisms and the composability of the morphisms are guaranteed by the reflexivity
Reflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
and the transitivity
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
of the preorder. By the same argument, any partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
and any equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
can be seen as a small category. Any ordinal number
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
can be seen as a category when viewed as an ordered set
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
.
Any monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
(any algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
with a single associative binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
and an identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
) forms a small category with a single object x. (Here, x is any fixed set.) The morphisms from x to x are precisely the elements of the monoid, the identity morphism of x is the identity of the monoid, and the categorical composition of morphisms is given by the monoid operation. Several definitions and theorems about monoids may be generalized for categories.
Any group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
can be seen as a category with a single object in which every morphism is invertible (for every morphism f there is a morphism g that is both left and right inverse to f under composition) by viewing the group as acting
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on itself by left multiplication. A morphism which is invertible in this sense is called an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
.
A groupoid
Groupoid
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
is a category in which every morphism is an isomorphism. Groupoids are generalizations of groups, group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
s and equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
s.
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
generates
Generating set
In mathematics, the expressions generator, generate, generated by and generating set can have several closely related technical meanings:...
a small category: the objects are the vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
of the graph, and the morphisms are the paths in the graph (augmented with loop
Loop (graph theory)
In graph theory, a loop is an edge that connects a vertex to itself. A simple graph contains no loops....
s as needed) where composition of morphisms is concatenation of paths. Such a category is called the free
Free object
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
category generated by the graph.
The class of all preordered sets with monotonic function
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
s as morphisms forms a category, Ord
Category of preordered sets
The category Ord has preordered sets as objects and monotonic functions as morphisms. This is a category because the composition of two monotonic functions is monotonic and the identity map is monotonic....
. It is a concrete category
Concrete category
In mathematics, a concrete category is a category that is equipped with a faithful functor to the category of sets. This functor makes it possible to think of the objects of the category as sets with additional structure, and of its morphisms as structure-preserving functions...
, i.e. a category obtained by adding some type of structure onto Set, and requiring that morphisms are functions that respect this added structure.
The class of all groups with group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
s as morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s and function composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
as the composition operation forms a large category, Grp
Category of groups
In mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
. Like Ord, Grp is a concrete category. The category Ab
Category of abelian groups
In mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category....
, consisting of all abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s and their group homomorphisms, is a full subcategory of Grp, and the prototype of an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
. Other examples of concrete categories are given by the following table.
| Category | Objects | Morphisms |
|---|---|---|
| Mag | magma Magma (algebra) In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M.... s |
magma homomorphisms |
| Manp Category of manifolds In mathematics, the category of manifolds, often denoted Manp, is the category whose objects are manifolds of smoothness class Cp and whose morphisms are p-times continuously differentiable maps... |
smooth manifolds | p-times continuously differentiable maps |
| Met Category of metric spaces In category-theoretic mathematics, Met is a category that has metric spaces as its objects and metric maps as its morphisms. This is a category because the composition of two metric maps is again a metric map... |
metric space Metric space In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space... s |
short map Short map In the mathematical theory of metric spaces, a metric map is a function between metric spaces that does not increase any distance .These maps are the morphisms in the category of metric spaces, Met .... s |
| R-Mod | R-Modules, where R is a Ring | module homomorphisms |
| Ring Category of rings In mathematics, the category of rings, denoted by Ring, is the category whose objects are rings and whose morphisms are ring homomorphisms... |
ring Ring (mathematics) In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition... s |
ring homomorphism Ring homomorphism In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication.... s |
| Set Category of sets In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B... |
sets | function Function (mathematics) In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can... s |
| Top Category of topological spaces In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous... |
topological space Topological space Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion... s |
continuous functions |
| Uni | uniform space Uniform space In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between... s |
uniformly continuous functions |
| VectK | vector space Vector space A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex... s over the field Field (mathematics) In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms... K |
K-linear maps |
Fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
s with bundle map
Bundle map
In mathematics, a bundle map is a morphism in the category of fiber bundles. There are two distinct, but closely related, notions of bundle map, depending on whether the fiber bundles in question have a common base space. There are also several variations on the basic theme, depending on precisely...
s between them form a concrete category.
The category Cat
Category of small categories
In mathematics, specifically in category theory, the category of small categories, denoted by Cat, is the category whose objects are all small categories and whose morphisms are functors between categories...
consists of all small categories, with functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s between them as morphisms.
Dual category
Any category C can itself be considered as a new category in a different way: the objects are the same as those in the original category but the arrows are those of the original category reversed. This is called the dual or opposite categoryDual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
and is denoted Cop.
Product categories
If C and D are categories, one can form the product category C × D: the objects are pairs consisting of one object from C and one from D, and the morphisms are also pairs, consisting of one morphism in C and one in D. Such pairs can be composed componentwise.Types of morphisms
A morphismMorphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
f : a → b is called
- a monomorphismMonomorphismIn the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
(or monic) if fg1 = fg2 implies g1 = g2 for all morphisms g1, g2 : x → a. - an epimorphismEpimorphismIn category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
(or epic) if g1f = g2f implies g1 = g2 for all morphisms g1, g2 : b → x. - a bimorphism if it is both a monomorphism and an epimorphism.
- a retraction if it has a right inverse, i.e. if there exists a morphism g : b → a with fg = 1b.
- a sectionSection (category theory)In category theory, a branch of mathematics, a section is a right inverse of a morphism. Dually, a retraction is a left inverse...
if it has a left inverse, i.e. if there exists a morphism g : b → a with gf = 1a. - an isomorphismIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
if it has an inverse, i.e. if there exists a morphism g : b → a with fg = 1b and gf = 1a. - an endomorphismEndomorphismIn mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
if a = b. The class of endomorphisms of a is denoted end(a). - an automorphismAutomorphismIn mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
if f is both an endomorphism and an isomorphism. The class of automorphisms of a is denoted aut(a).
Every retraction is an epimorphism. Every section is a monomorphism. The following three statements are equivalent:
- f is a monomorphism and a retraction;
- f is an epimorphism and a section;
- f is an isomorphism.
Relations among morphisms (such as fg = h) can most conveniently be represented with commutative diagram
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
s, where the objects are represented as points and the morphisms as arrows.
Types of categories
- In many categories, e.g. AbCategory of abelian groupsIn mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category....
or VectK, the hom-sets hom(a, b) are not just sets but actually abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s, and the composition of morphisms is compatible with these group structures; i.e. is bilinearBilinearBilinear may refer to:* Bilinear sampling, a method in computer graphics for choosing the color of a texture* Bilinear form* Bilinear interpolation* Bilinear map, a type of mathematical function between vector spaces...
. Such a category is called preadditivePreadditive categoryIn mathematics, specifically in category theory, a preadditive category is a category that is enriched over the monoidal category of abelian groups...
. If, furthermore, the category has all finite productsProduct (category theory)In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
and coproductCoproductIn category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
s, it is called an additive categoryAdditive categoryIn mathematics, specifically in category theory, an additive category is a preadditive category C such that all finite collections of objects A1,...,An of C have a biproduct A1 ⊕ ⋯ ⊕ An in C....
. If all morphisms have a kernelKernel (category theory)In category theory and its applications to other branches of mathematics, kernels are a generalization of the kernels of group homomorphisms, the kernels of module homomorphisms and certain other kernels from algebra...
and a cokernelCokernelIn mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
, and all epimorphisms are cokernels and all monomorphisms are kernels, then we speak of an abelian categoryAbelian categoryIn mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
. A typical example of an abelian category is the category of abelian groups. - A category is called completeComplete categoryIn mathematics, a complete category is a category in which all small limits exist. That is, a category C is complete if every diagram F : J → C where J is small has a limit in C. Dually, a cocomplete category is one in which all small colimits exist...
if all limitsLimit (category theory)In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
exist in it. The categories of sets, abelian groups and topological spaces are complete. - A category is called cartesian closedCartesian closed categoryIn category theory, a category is cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in...
if it has finite direct products and a morphism defined on a finite product can always be represented by a morphism defined on just one of the factors. Examples include SetCategory of setsIn the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
and CPO, the category of complete partial orderComplete partial orderIn mathematics, directed complete partial orders and ω-complete partial orders are special classes of partially ordered sets, characterized by particular completeness properties...
s with Scott-continuous functionsScott continuityIn mathematics, given two partially ordered sets P and Q a function f : P \rightarrow Q between them is Scott-continuous if it preserves all directed suprema, i.e...
. - A toposToposIn mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
is a certain type of cartesian closed category in which all of mathematics can be formulated (just like classically all of mathematics is formulated in the category of sets). A topos can also be used to represent a logical theory.
See also
- Enriched categoryEnriched categoryIn category theory and its applications to mathematics, enriched category is a generalization of category that abstracts the set of morphisms associated with every pair of objects to an opaque object in some fixed monoidal category of "hom-objects" and then defines composition and identity solely...
- Higher category theoryHigher category theoryHigher category theory is the part of category theory at a higher order, which means that some equalities are replaced by explicit arrows in order to be able to explicitly study the structure behind those equalities.- Strict higher categories :...
- Table of mathematical symbolsTable of mathematical symbolsThis is a listing of common symbols found within all branches of mathematics. Each symbol is listed in both HTML, which depends on appropriate fonts being installed, and in , as an image.-Symbols:-Variations:...