Module (mathematics)
Encyclopedia
In abstract algebra
, the concept of a module over a ring
is a generalization of the notion of vector space
, wherein the corresponding scalars
are allowed to lie in an arbitrary ring. Modules also generalize the notion of abelian group
s, which are modules over the ring of integers
.
Thus, a module, like a vector space, is an additive abelian group; a product is defined between elements of the ring and elements of the module, and this multiplication is associative (when used with the multiplication in the ring) and distributive.
Modules are very closely related to the representation theory
of group
s. They are also one of the central notions of commutative algebra
and homological algebra
, and are used widely in algebraic geometry
and algebraic topology
.
forms a field
and acts on the vectors by scalar multiplication, subject to certain axioms such as the distributive law. In a module, the scalars need only be a ring
, so the module concept represents a significant generalization. In commutative algebra, it is important that both ideals
and quotient ring
s are modules, so that many arguments about ideals or quotient rings can be combined into a single argument about modules. In non-commutative algebra the distinction between left ideals, ideals, and modules becomes more pronounced, though some important ring theoretic conditions can be expressed either about left ideals or left modules.
Much of the theory of modules consists of extending as many as possible of the desirable properties of vector spaces to the realm of modules over a "well-behaved
" ring, such as a principal ideal domain
. However, modules can be quite a bit more complicated than vector spaces; for instance, not all modules have a basis
, and even those that do, free module
s, need not have a unique rank if the underlying ring does not satisfy the invariant basis number
condition, unlike vector spaces which always have a basis whose cardinality is then unique (assuming the axiom of choice).
R consists of an abelian group
(M, +) and an operation R × M → M such that for all r,s in R, x,y in M, we have:
The operation of the ring on M is called scalar multiplication, and is usually written by juxtaposition, i.e. as rx for r in R and x in M. The notation RM indicates a left R-module M". A right R-module M or MR is defined similarly, only the ring acts on the right, i.e. we have a scalar multiplication of the form M × R → M, and the above axioms are written with scalars r and s on the right of x and y.
Authors who do not require rings to be unital omit condition 4 above in the definition of an R-module, and so would call the structures defined above "unital left R-modules". In this article, consistent with the glossary of ring theory
, all rings and modules are assumed to be unital.
If one writes the scalar action as fr so that fr(x) = rx, and f for the map which takes each r to its corresponding map fr , then the first axiom states that every fr is a group homomorphism
of M, and the other three axioms assert that the map f:R → End(M) given by r ↦fr is a ring homomorphism
from R to the endomorphism ring
End(M). Thus a module is a ring action on an abelian group (cf. group action
. Also consider Monoid action of multiplicative structure of R). In this sense, module theory generalizes representation theory
, which deals with group actions on vector spaces, or equivalently group ring
actions.
A bimodule
is a module which is a left module and a right module such that the two multiplications are compatible.
If R is commutative
, then left R-modules are the same as right R-modules and are simply called R-modules.
of M. Then N is a submodule (or R-submodule, to be more explicit) if, for any n in N and any r in R, the product r n is in N (or nr for a right module).
The set of submodules of a given module M, together with the two binary operations + and ∩, forms a lattice
which satisfies the modular law
:
Given submodules U, N1, N2 of M such that N1 ⊂ N2, then the following two submodules are equal: (N1 + U) ∩ N2 = N1 + (U ∩ N2).
If M and N are left R-modules, then a map
f : M → N is a homomorphism of R-modules if, for any m, n in M
and r, s in R,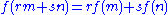
This, like any homomorphism
of mathematical
objects, is just a mapping which preserves the structure of the objects.
Another name for a homomorphism of modules over R is an R-linear map.
A bijective module homomorphism is an isomorphism
of modules, and the two modules are called isomorphic. Two isomorphic modules are identical for all practical purposes, differing solely in the notation for their elements.
The kernel
of a module homomorphism f : M → N is the submodule of M consisting of all elements that are sent to zero by f. The isomorphism theorem
s familiar from groups and vector spaces are also valid for R-modules.
The left R-modules, together with their module homomorphisms, form a category
, written as R-Mod. This is an abelian category
.
of those elements with coefficients from the scalar ring R.
Cyclic module. A module is called a cyclic module
if it is generated by one element.
Free. A free module
is a module that has a basis, or equivalently, one that is isomorphic to a direct sum
of copies of the scalar ring R. These are the modules that behave very much like vector spaces.
Projective. Projective module
s are direct summands of free modules and share many of their desirable properties.
Injective. Injective module
s are defined dually to projective modules.
Flat. A module is called flat
if taking the tensor product
of it with any short exact sequence of R modules preserves exactness.
Simple. A simple module
S is a module that is not {0} and whose only submodules are {0} and S. Simple modules are sometimes called irreducible.
Semisimple. A semisimple module
is a direct sum (finite or not) of simple modules. Historically these modules are also called completely reducible.
Indecomposable. An indecomposable module
is a non-zero module that cannot be written as a direct sum
of two non-zero submodules. Every simple module is indecomposable, but there are indecomposable modules which are not simple (e.g. uniform module
s).
Faithful. A faithful module M is one where the action of each r ≠ 0 in R on M is nontrivial (i.e. rx ≠ 0 for some x in M). Equivalently, the annihilator
of M is the zero ideal.
Noetherian. A Noetherian module
is a module which satisfies the ascending chain condition
on submodules, that is, every increasing chain of submodules becomes stationary after finitely many steps. Equivalently, every submodule is finitely generated.
Artinian. An Artinian module
is a module which satisfies the descending chain condition on submodules, that is, every decreasing chain of submodules becomes stationary after finitely many steps.
Graded. A graded module is a module decomposable as a direct sum M = ⊕x Mx over a graded ring R = ⊕x Rx such that RxMy ⊂ Mx + y for all x and y.
Uniform. A uniform module
is a module in which all pairs of nonzero submodules have nonzero intersection.
of the abelian group (M,+). The set of all group endomorphisms of M is denoted EndZ(M) and forms a ring under addition and composition, and sending a ring element r of R to its action actually defines a ring homomorphism
from R to EndZ(M).
Such a ring homomorphism R → EndZ(M) is called a representation of R over the abelian group M; an alternative and equivalent way of defining left R-modules is to say that a left R-module is an abelian group M together with a representation of R over it.
A representation is called faithful if and only if the map R → EndZ(M) is injective. In terms of modules, this means that if r is an element of R such that rx=0 for all x in M, then r=0. Every abelian group is a faithful module over the integer
s or over some modular arithmetic
Z/nZ.
with a single object. With this understanding, a left R-module is nothing but a (covariant) additive functor from R to the category Ab of abelian groups. Right R-modules are contravariant additive functors. This suggests that, if C is any preadditive category, a covariant additive functor from C to Ab should be considered a generalized left module over C; these functors form a functor category
C-Mod which is the natural generalization of the module category R-Mod.
Modules over commutative rings can be generalized in a different direction: take a ringed space
(X, OX) and consider the sheaves
of OX-modules. These form a category OX-Mod, and play an important role in the scheme
-theoretic approach to algebraic geometry
. If X has only a single point, then this is a module category in the old sense over the commutative ring OX(X).
One can also consider modules over a semiring
. Modules over rings are abelian groups, but modules over semirings are only commutative monoid
s. Most applications of modules are still possible. In particular, for any semiring
S the matrices over S form a semiring over which the tuples of elements from S are a module (in this generalized sense only). This allows a further generalization of the concept of vector space
incorporating the semirings from theoretical computer science.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the concept of a module over a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
is a generalization of the notion of vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, wherein the corresponding scalars
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
are allowed to lie in an arbitrary ring. Modules also generalize the notion of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s, which are modules over the ring of integers
Ring of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
.
Thus, a module, like a vector space, is an additive abelian group; a product is defined between elements of the ring and elements of the module, and this multiplication is associative (when used with the multiplication in the ring) and distributive.
Modules are very closely related to the representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s. They are also one of the central notions of commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
and homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
, and are used widely in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
and algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
.
Motivation
In a vector space, the set of scalarsScalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
forms a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
and acts on the vectors by scalar multiplication, subject to certain axioms such as the distributive law. In a module, the scalars need only be a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, so the module concept represents a significant generalization. In commutative algebra, it is important that both ideals
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
and quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
s are modules, so that many arguments about ideals or quotient rings can be combined into a single argument about modules. In non-commutative algebra the distinction between left ideals, ideals, and modules becomes more pronounced, though some important ring theoretic conditions can be expressed either about left ideals or left modules.
Much of the theory of modules consists of extending as many as possible of the desirable properties of vector spaces to the realm of modules over a "well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
" ring, such as a principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
. However, modules can be quite a bit more complicated than vector spaces; for instance, not all modules have a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
, and even those that do, free module
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
s, need not have a unique rank if the underlying ring does not satisfy the invariant basis number
Invariant basis number
In mathematics, the invariant basis number property of a ring R is the property that all free modules over R are similarly well-behaved as vector spaces, with respect to the uniqueness of their ranks.-Definition:...
condition, unlike vector spaces which always have a basis whose cardinality is then unique (assuming the axiom of choice).
Formal definition
A left R-module M over the ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R consists of an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
(M, +) and an operation R × M → M such that for all r,s in R, x,y in M, we have:
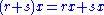
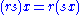
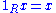if R has multiplicative identity 
The operation of the ring on M is called scalar multiplication, and is usually written by juxtaposition, i.e. as rx for r in R and x in M. The notation RM indicates a left R-module M". A right R-module M or MR is defined similarly, only the ring acts on the right, i.e. we have a scalar multiplication of the form M × R → M, and the above axioms are written with scalars r and s on the right of x and y.
Authors who do not require rings to be unital omit condition 4 above in the definition of an R-module, and so would call the structures defined above "unital left R-modules". In this article, consistent with the glossary of ring theory
Glossary of ring theory
Ring theory is the branch of mathematics in which rings are studied: that is, structures supporting both an addition and a multiplication operation. This is a glossary of some terms of the subject.-Definition of a ring:...
, all rings and modules are assumed to be unital.
If one writes the scalar action as fr so that fr(x) = rx, and f for the map which takes each r to its corresponding map fr , then the first axiom states that every fr is a group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
of M, and the other three axioms assert that the map f:R → End(M) given by r ↦fr is a ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
from R to the endomorphism ring
Endomorphism ring
In abstract algebra, one associates to certain objects a ring, the object's endomorphism ring, which encodes several internal properties of the object; this may be denoted End...
End(M). Thus a module is a ring action on an abelian group (cf. group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
. Also consider Monoid action of multiplicative structure of R). In this sense, module theory generalizes representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, which deals with group actions on vector spaces, or equivalently group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
actions.
A bimodule
Bimodule
In abstract algebra a bimodule is an abelian group that is both a left and a right module, such that the left and right multiplications are compatible...
is a module which is a left module and a right module such that the two multiplications are compatible.
If R is commutative
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
, then left R-modules are the same as right R-modules and are simply called R-modules.
Examples
- If K is a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, then the concepts "K-vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
" (a vector space over K) and K-module are identical. - The concept of a Z-module agrees with the notion of an abelian group. That is, every abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
is a module over the ring of integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s Z in a unique way. For n > 0, let nx = x + x + ... + x (n summands), 0x = 0, and (−n)x = −(nx). Such a module need not have a basisBasis (linear algebra)In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
—groups containing torsion elements do not. (For example, in the group of integers moduloModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
3, one cannot find even one element which satisfies the definition of a linearly independent set since when an integer such as 3 or 6 multiplies an element the result is 0. However if a finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
is considered as a module over the same finite field taken as a ring, it is a vector space and does have a basis.) - If R is any ring and n a natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
, then the cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
Rn is both a left and a right module over R if we use the component-wise operations. Hence when n = 1, R is an R-module, where the scalar multiplication is just ring multiplication. The case n = 0 yields the trivial R-module {0} consisting only of its identity element. Modules of this type are called freeFree moduleIn mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
and if R has invariant basis numberInvariant basis numberIn mathematics, the invariant basis number property of a ring R is the property that all free modules over R are similarly well-behaved as vector spaces, with respect to the uniqueness of their ranks.-Definition:...
(e.g. any commutative ring or field) the number n is then the rank of the free module. - If S is a nonempty set, M is a left R-module, and MS is the collection of all functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s f : S → M, then with addition and scalar multiplication in MS defined by (f + g)(s) = f(s) + g(s) and (rf)(s) = rf(s), MS is a left R-module. The right R-module case is analogous. In particular, if R is commutative then the collection of R-module homomorphisms h : M → N (see below) is an R-module (and in fact a submodule of NM). - If X is a smooth manifold, then the smooth functionSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s from X to the real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s form a ring C∞(X). The set of all smooth vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s defined on X form a module over C∞(X), and so do the tensor fieldTensor fieldIn mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
s and the differential formDifferential formIn the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s on X. More generally, the sections of any vector bundleVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
form a projective moduleProjective moduleIn mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
over C∞(X), and by Swan's theoremSwan's theoremIn the mathematical fields of topology and K-theory, the Serre–Swan theorem, also called Swan's theorem, relates the geometric notion of vector bundles to the algebraic concept of projective modules and gives rise to a common intuition throughout mathematics: "projective modules over commutative...
, every projective module is isomorphic to the module of sections of some bundle; the categoryCategory (mathematics)In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of C∞(X)-modules and the category of vector bundles over X are equivalentEquivalence of categoriesIn category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
. - The square n-by-n matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with real entries form a ring R, and the Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn is a left module over this ring if we define the module operation via matrix multiplicationMatrix multiplicationIn mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
. - If R is any ring and I is any left ideal in R, then I is a left module over R. Analogously of course, right ideals are right modules.
- If R is a ring, we can define the ring Rop which has the same underlying set and the same addition operation, but the opposite multiplication: if ab = c in R, then ba = c in Rop. Any left R-module M can then be seen to be a right module over Rop, and any right module over R can be considered a left module over Rop.
- There are modules of a Lie algebra as well.
Submodules and homomorphisms
Suppose M is a left R-module and N is a subgroupSubgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of M. Then N is a submodule (or R-submodule, to be more explicit) if, for any n in N and any r in R, the product r n is in N (or nr for a right module).
The set of submodules of a given module M, together with the two binary operations + and ∩, forms a lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
which satisfies the modular law
Modular lattice
In the branch of mathematics called order theory, a modular lattice is a lattice that satisfies the following self-dual condition:Modular law: x ≤ b implies x ∨ = ∧ b,where ≤ is the partial order, and ∨ and ∧ are...
:
Given submodules U, N1, N2 of M such that N1 ⊂ N2, then the following two submodules are equal: (N1 + U) ∩ N2 = N1 + (U ∩ N2).
If M and N are left R-modules, then a map
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
f : M → N is a homomorphism of R-modules if, for any m, n in M
and r, s in R,
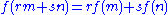
This, like any homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
of mathematical
objects, is just a mapping which preserves the structure of the objects.
Another name for a homomorphism of modules over R is an R-linear map.
A bijective module homomorphism is an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
of modules, and the two modules are called isomorphic. Two isomorphic modules are identical for all practical purposes, differing solely in the notation for their elements.
The kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of a module homomorphism f : M → N is the submodule of M consisting of all elements that are sent to zero by f. The isomorphism theorem
Isomorphism theorem
In mathematics, specifically abstract algebra, the isomorphism theorems are three theorems that describe the relationship between quotients, homomorphisms, and subobjects. Versions of the theorems exist for groups, rings, vector spaces, modules, Lie algebras, and various other algebraic structures...
s familiar from groups and vector spaces are also valid for R-modules.
The left R-modules, together with their module homomorphisms, form a category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, written as R-Mod. This is an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
.
Types of modules
Finitely generated. A module M is finitely generated if there exist finitely many elements x1,...,xn in M such that every element of M is a linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of those elements with coefficients from the scalar ring R.
Cyclic module. A module is called a cyclic module
Cyclic module
In mathematics, more specifically in ring theory, a cyclic module is a module over a ring which is generated by one element. The term is by analogy with cyclic groups, that is groups which are generated by one element.- Definition :...
if it is generated by one element.
Free. A free module
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
is a module that has a basis, or equivalently, one that is isomorphic to a direct sum
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
of copies of the scalar ring R. These are the modules that behave very much like vector spaces.
Projective. Projective module
Projective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
s are direct summands of free modules and share many of their desirable properties.
Injective. Injective module
Injective module
In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module Q that shares certain desirable properties with the Z-module Q of all rational numbers...
s are defined dually to projective modules.
Flat. A module is called flat
Flat module
In Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
if taking the tensor product
Tensor product of modules
In mathematics, the tensor product of modules is a construction that allows arguments about bilinear maps to be carried out in terms of linear maps...
of it with any short exact sequence of R modules preserves exactness.
Simple. A simple module
Simple module
In mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
S is a module that is not {0} and whose only submodules are {0} and S. Simple modules are sometimes called irreducible.
Semisimple. A semisimple module
Semisimple module
In mathematics, especially in the area of abstract algebra known as module theory, a semisimple module or completely reducible module is a type of module that can be understood easily from its parts. A ring which is a semisimple module over itself is known as an artinian semisimple ring...
is a direct sum (finite or not) of simple modules. Historically these modules are also called completely reducible.
Indecomposable. An indecomposable module
Indecomposable module
In abstract algebra, a module is indecomposable if it is non-zero and cannot be written as a direct sum of two non-zero submodules.Indecomposable is a weaker notion than simple module:simple means "no proper submodule" N...
is a non-zero module that cannot be written as a direct sum
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
of two non-zero submodules. Every simple module is indecomposable, but there are indecomposable modules which are not simple (e.g. uniform module
Uniform module
In abstract algebra, a module is called a uniform module if the intersection of any two nonzero submodules is nonzero. This is equivalent to saying that every nonzero submodule of M is an essential submodule...
s).
Faithful. A faithful module M is one where the action of each r ≠ 0 in R on M is nontrivial (i.e. rx ≠ 0 for some x in M). Equivalently, the annihilator
Annihilator (ring theory)
In mathematics, specifically module theory, annihilators are a concept that generalizes torsion and orthogonal complement.-Definitions:Let R be a ring, and let M be a left R-module. Choose a nonempty subset S of M...
of M is the zero ideal.
Noetherian. A Noetherian module
Noetherian module
In abstract algebra, an Noetherian module is a module that satisfies the ascending chain condition on its submodules, where the submodules are partially ordered by inclusion....
is a module which satisfies the ascending chain condition
Ascending chain condition
The ascending chain condition and descending chain condition are finiteness properties satisfied by some algebraic structures, most importantly, ideals in certain commutative rings...
on submodules, that is, every increasing chain of submodules becomes stationary after finitely many steps. Equivalently, every submodule is finitely generated.
Artinian. An Artinian module
Artinian module
In abstract algebra, an Artinian module is a module that satisfies the descending chain condition on its poset of submodules. They are for modules what Artinian rings are for rings, and a ring is Artinian if and only if it is an Artinian module over itself...
is a module which satisfies the descending chain condition on submodules, that is, every decreasing chain of submodules becomes stationary after finitely many steps.
Graded. A graded module is a module decomposable as a direct sum M = ⊕x Mx over a graded ring R = ⊕x Rx such that RxMy ⊂ Mx + y for all x and y.
Uniform. A uniform module
Uniform module
In abstract algebra, a module is called a uniform module if the intersection of any two nonzero submodules is nonzero. This is equivalent to saying that every nonzero submodule of M is an essential submodule...
is a module in which all pairs of nonzero submodules have nonzero intersection.
Relation to representation theory
If M is a left R-module, then the action of an element r in R is defined to be the map M → M that sends each x to rx (or xr in the case of a right module), and is necessarily a group endomorphismGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
of the abelian group (M,+). The set of all group endomorphisms of M is denoted EndZ(M) and forms a ring under addition and composition, and sending a ring element r of R to its action actually defines a ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
from R to EndZ(M).
Such a ring homomorphism R → EndZ(M) is called a representation of R over the abelian group M; an alternative and equivalent way of defining left R-modules is to say that a left R-module is an abelian group M together with a representation of R over it.
A representation is called faithful if and only if the map R → EndZ(M) is injective. In terms of modules, this means that if r is an element of R such that rx=0 for all x in M, then r=0. Every abelian group is a faithful module over the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s or over some modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
Z/nZ.
Generalizations
Any ring R can be viewed as a preadditive categoryPreadditive category
In mathematics, specifically in category theory, a preadditive category is a category that is enriched over the monoidal category of abelian groups...
with a single object. With this understanding, a left R-module is nothing but a (covariant) additive functor from R to the category Ab of abelian groups. Right R-modules are contravariant additive functors. This suggests that, if C is any preadditive category, a covariant additive functor from C to Ab should be considered a generalized left module over C; these functors form a functor category
Functor category
In category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
C-Mod which is the natural generalization of the module category R-Mod.
Modules over commutative rings can be generalized in a different direction: take a ringed space
Ringed space
In mathematics, a ringed space is, intuitively speaking, a space together with a collection of commutative rings, the elements of which are "functions" on each open set of the space...
(X, OX) and consider the sheaves
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of OX-modules. These form a category OX-Mod, and play an important role in the scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
-theoretic approach to algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. If X has only a single point, then this is a module category in the old sense over the commutative ring OX(X).
One can also consider modules over a semiring
Semiring
In abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
. Modules over rings are abelian groups, but modules over semirings are only commutative monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
s. Most applications of modules are still possible. In particular, for any semiring
Semiring
In abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
S the matrices over S form a semiring over which the tuples of elements from S are a module (in this generalized sense only). This allows a further generalization of the concept of vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
incorporating the semirings from theoretical computer science.