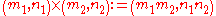Rational number
Encyclopedia
In mathematics
, a rational number is any number
that can be expressed as the quotient
or fraction a/b of two integer
s, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number. The set of all rational numbers is usually denoted by a boldface Q (or blackboard bold
 , Unicode
, Unicode
, which stands for quotient
.)
The decimal expansion of a rational number always either terminates after finitely many digits
or begins to repeat
the same finite sequence
of digits over and over. Moreover, any repeating or terminating decimal represents a rational number. These statements hold true not just for base 10
, but also for binary
, hexadecimal
, or any other integer base
.
A real number
that is not rational is called irrational
. Irrational numbers include √2
, π
, and e
. The decimal expansion of an irrational number continues forever without repeating. Since the set of rational numbers is countable
, and the set of real numbers is uncountable
, almost all
real numbers are irrational.
The rational numbers can be formally
defined as the equivalence classes of the quotient set where the cartesian product
is the set of all ordered pair
s (m,n) where m and n are integer
s, n is not zero (n ≠ 0), and "~" is the equivalence relation
defined by if, and only if
,
In abstract algebra
, the rational numbers together with certain operations of addition
and multiplication
form a field
. This is the archetypical field of characteristic
zero, and is the field of fractions
for the ring
of integers. Finite extensions
of Q are called algebraic number field
s, and the algebraic closure
of Q is the field of algebraic number
s.
In mathematical analysis
, the rational numbers form a dense subset
of the real numbers. The real numbers can be constructed from the rational numbers by completion, using either Cauchy sequence
s, Dedekind cut
s, or infinite decimal
s.
Zero divided by any other integer equals zero, therefore zero is a rational number (but division by zero
is undefined).
of two integers. In mathematics, the adjective rational often means that the underlying field
considered is the field Q of rational numbers. Rational polynomial usually, and most correctly, means a polynomial with rational coefficients, also called a “polynomial over the rationals”. However, rational function
does not mean the underlying field is the rational numbers, and a rational algebraic curve
is not an algebraic curve with rational coefficients.
Two fractions are added as follows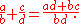
The rule for multiplication is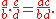
Additive
and multiplicative inverse
s exist in the rational numbers
It follows that the quotient of two fractions is given by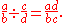
of positive integers, such as
For any positive rational number, there are infinitely many different such representations, called Egyptian fractions, as they were used by the ancient Egyptians
. The Egyptians also had a different notation for dyadic fractions in the Akhmim Wooden Tablet
and several Rhind Mathematical Papyrus
problems.
s of integer
s (m,n), with n ≠ 0. This space of equivalence classes is the quotient space
where if, and only if, We can define addition and multiplication of these pairs with the following rules:
and, if m2 ≠ 0, division by
The equivalence relation (m1,n1) ~ (m2,n2) if, and only if, is a congruence relation
, i.e. it is compatible with the addition and multiplication defined above, and we may define Q to be the quotient set i.e. we identify two pairs (m1,n1) and (m2,n2) if they are equivalent in the above sense. (This construction can be carried out in any integral domain: see field of fractions
.) We denote by [(m1,n1)] the equivalence class containing (m1,n1). If (m1,n1) ~ (m2,n2) then, by definition, (m1,n1) belongs to [(m2,n2)] and (m2,n2) belongs to [(m1,n1)]; in this case we can write [(m1,n1)] = [(m2,n2)]. Given any equivalence class [(m,n)] there are a countably infinite number of representation, since

The canonical choice for [(m,n)] is chosen so that gcd
(m,n) = 1, i.e. m and n share no common factors, i.e. m and n are coprime
. For example, we would write [(1,2)] instead of [(2,4)] or [(−12,−24)], even though [(1,2)] = [(2,4)] = [(−12,−24)].
We can also define a total order
on Q. Let ∧ be the and-symbol and ∨ be the or-symbol. We say that if:
The integers may be considered to be rational numbers by the embedding
that maps m to [(m, 1)].
, the field of fractions
of the integer
s Z.
The rationals are the smallest field with characteristic
zero: every other field of characteristic zero contains a copy of Q. The rational numbers are therefore the prime field for characteristic zero.
The algebraic closure
of Q, i.e. the field of roots of rational polynomials, is the algebraic number
s.
The set of all rational numbers is countable. Since the set of all real numbers is uncountable, we say that almost all
real numbers are irrational, in the sense of Lebesgue measure
, i.e. the set of rational numbers is a null set
.
The rationals are a densely ordered set: between any two rationals, there sits another one, and, therefore, infinitely many other ones. Any totally ordered set which is countable, dense (in the above sense), and has no least or greatest element is order isomorphic
to the rational numbers.
of the real numbers: every real number has rational numbers arbitrarily close to it. A related property is that rational numbers are the only numbers with finite expansions as regular continued fractions
.
By virtue of their order, the rationals carry an order topology
. The rational numbers, as a subspace of the real numbers, also carry a subspace topology
. The rational numbers form a metric space
by using the absolute difference
metric and this yields a third topology on Q. All three topologies coincide and turn the rationals into a topological field. The rational numbers are an important example of a space which is not locally compact. The rationals are characterized topologically as the unique countable metrizable space
without isolated point
s.
The space is also totally disconnected
. The rational numbers do not form a complete metric space; the real numbers are the completion of Q under the metric above.
Let p be a prime number
and for any non-zero integer a, let where pn is the highest power of p dividing
a.
In addition set For any rational number a/b, we set
Then defines a metric
on Q.
The metric space (Q,dp) is not complete, and its completion is the p-adic number field
Qp. Ostrowski's theorem
states that any non-trivial absolute value
on the rational numbers Q is equivalent to either the usual real absolute value or a p-adic
absolute value.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a rational number is any number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
that can be expressed as the quotient
Quotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
or fraction a/b of two integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number. The set of all rational numbers is usually denoted by a boldface Q (or blackboard bold
Blackboard bold
Blackboard bold is a typeface style that is often used for certain symbols in mathematical texts, in which certain lines of the symbol are doubled. The symbols usually denote number sets...
 , Unicode
, UnicodeUnicode
Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems...
, which stands for quotient
Quotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
.)
The decimal expansion of a rational number always either terminates after finitely many digits
Numerical digit
A digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
or begins to repeat
Repeating decimal
In arithmetic, a decimal representation of a real number is called a repeating decimal if at some point it becomes periodic, that is, if there is some finite sequence of digits that is repeated indefinitely...
the same finite sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of digits over and over. Moreover, any repeating or terminating decimal represents a rational number. These statements hold true not just for base 10
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
, but also for binary
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
, hexadecimal
Hexadecimal
In mathematics and computer science, hexadecimal is a positional numeral system with a radix, or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F to represent values ten to fifteen...
, or any other integer base
Radix
In mathematical numeral systems, the base or radix for the simplest case is the number of unique digits, including zero, that a positional numeral system uses to represent numbers. For example, for the decimal system the radix is ten, because it uses the ten digits from 0 through 9.In any numeral...
.
A real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
that is not rational is called irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
. Irrational numbers include √2
Square root of 2
The square root of 2, often known as root 2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.Geometrically the square root of 2 is the...
, π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, and e
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
. The decimal expansion of an irrational number continues forever without repeating. Since the set of rational numbers is countable
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
, and the set of real numbers is uncountable
Uncountable set
In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...
, almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
real numbers are irrational.
The rational numbers can be formally
Formalism (mathematics)
In foundations of mathematics, philosophy of mathematics, and philosophy of logic, formalism is a theory that holds that statements of mathematics and logic can be thought of as statements about the consequences of certain string manipulation rules....
defined as the equivalence classes of the quotient set where the cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
is the set of all ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
s (m,n) where m and n are integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, n is not zero (n ≠ 0), and "~" is the equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
defined by if, and only if
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
,
In abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the rational numbers together with certain operations of addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
form a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. This is the archetypical field of characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
zero, and is the field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
for the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of integers. Finite extensions
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
of Q are called algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
s, and the algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of Q is the field of algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s.
In mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, the rational numbers form a dense subset
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
of the real numbers. The real numbers can be constructed from the rational numbers by completion, using either Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
s, Dedekind cut
Dedekind cut
In mathematics, a Dedekind cut, named after Richard Dedekind, is a partition of the rationals into two non-empty parts A and B, such that all elements of A are less than all elements of B, and A contains no greatest element....
s, or infinite decimal
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
s.
Zero divided by any other integer equals zero, therefore zero is a rational number (but division by zero
Division by zero
In mathematics, division by zero is division where the divisor is zero. Such a division can be formally expressed as a / 0 where a is the dividend . Whether this expression can be assigned a well-defined value depends upon the mathematical setting...
is undefined).
Terminology
The term rational in reference to the set Q refers to the fact that a rational number represents a ratioRatio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
of two integers. In mathematics, the adjective rational often means that the underlying field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
considered is the field Q of rational numbers. Rational polynomial usually, and most correctly, means a polynomial with rational coefficients, also called a “polynomial over the rationals”. However, rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
does not mean the underlying field is the rational numbers, and a rational algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
is not an algebraic curve with rational coefficients.
Arithmetic
Two rational numbers a/b and c/d are equal if, and only if,Two fractions are added as follows
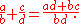
The rule for multiplication is
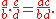
Additive
Additive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
and multiplicative inverse
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
s exist in the rational numbers

It follows that the quotient of two fractions is given by
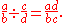
Egyptian fractions
Any positive rational number can be expressed as a sum of distinct reciprocalsMultiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of positive integers, such as

For any positive rational number, there are infinitely many different such representations, called Egyptian fractions, as they were used by the ancient Egyptians
Egyptians
Egyptians are nation an ethnic group made up of Mediterranean North Africans, the indigenous people of Egypt.Egyptian identity is closely tied to geography. The population of Egypt is concentrated in the lower Nile Valley, the small strip of cultivable land stretching from the First Cataract to...
. The Egyptians also had a different notation for dyadic fractions in the Akhmim Wooden Tablet
Akhmim wooden tablet
The Akhmim wooden tablets or Cairo wooden tablets are two ancient Egyptian wooden writing tablets. They each measure about 18 by 10 inches and are covered with plaster. The tablets are inscribed on both sides. The inscriptions on the first tablet includes a list of servants, which is followed...
and several Rhind Mathematical Papyrus
Rhind Mathematical Papyrus
The Rhind Mathematical Papyrus , is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum. It dates to around 1650 BC...
problems.
Formal construction
Mathematically we may construct the rational numbers as equivalence classes of ordered pairOrdered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
s of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s (m,n), with n ≠ 0. This space of equivalence classes is the quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
where if, and only if, We can define addition and multiplication of these pairs with the following rules:
and, if m2 ≠ 0, division by
The equivalence relation (m1,n1) ~ (m2,n2) if, and only if, is a congruence relation
Congruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
, i.e. it is compatible with the addition and multiplication defined above, and we may define Q to be the quotient set i.e. we identify two pairs (m1,n1) and (m2,n2) if they are equivalent in the above sense. (This construction can be carried out in any integral domain: see field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
.) We denote by [(m1,n1)] the equivalence class containing (m1,n1). If (m1,n1) ~ (m2,n2) then, by definition, (m1,n1) belongs to [(m2,n2)] and (m2,n2) belongs to [(m1,n1)]; in this case we can write [(m1,n1)] = [(m2,n2)]. Given any equivalence class [(m,n)] there are a countably infinite number of representation, since

The canonical choice for [(m,n)] is chosen so that gcd
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
(m,n) = 1, i.e. m and n share no common factors, i.e. m and n are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
. For example, we would write [(1,2)] instead of [(2,4)] or [(−12,−24)], even though [(1,2)] = [(2,4)] = [(−12,−24)].
We can also define a total order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
on Q. Let ∧ be the and-symbol and ∨ be the or-symbol. We say that if:

The integers may be considered to be rational numbers by the embedding
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
that maps m to [(m, 1)].
Properties
The set Q, together with the addition and multiplication operations shown above, forms a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, the field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
of the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s Z.
The rationals are the smallest field with characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
zero: every other field of characteristic zero contains a copy of Q. The rational numbers are therefore the prime field for characteristic zero.
The algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of Q, i.e. the field of roots of rational polynomials, is the algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s.
The set of all rational numbers is countable. Since the set of all real numbers is uncountable, we say that almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
real numbers are irrational, in the sense of Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
, i.e. the set of rational numbers is a null set
Null set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
.
The rationals are a densely ordered set: between any two rationals, there sits another one, and, therefore, infinitely many other ones. Any totally ordered set which is countable, dense (in the above sense), and has no least or greatest element is order isomorphic
Order isomorphism
In the mathematical field of order theory an order isomorphism is a special kind of monotone function that constitutes a suitable notion of isomorphism for partially ordered sets . Whenever two posets are order isomorphic, they can be considered to be "essentially the same" in the sense that one of...
to the rational numbers.
Real numbers and topological properties
The rationals are a dense subsetDense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
of the real numbers: every real number has rational numbers arbitrarily close to it. A related property is that rational numbers are the only numbers with finite expansions as regular continued fractions
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
.
By virtue of their order, the rationals carry an order topology
Order topology
In mathematics, an order topology is a certain topology that can be defined on any totally ordered set. It is a natural generalization of the topology of the real numbers to arbitrary totally ordered sets...
. The rational numbers, as a subspace of the real numbers, also carry a subspace topology
Subspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
. The rational numbers form a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
by using the absolute difference
Absolute difference
The absolute difference of two real numbers x, y is given by |x − y|, the absolute value of their difference. It describes the distance on the real line between the points corresponding to x and y...
metric and this yields a third topology on Q. All three topologies coincide and turn the rationals into a topological field. The rational numbers are an important example of a space which is not locally compact. The rationals are characterized topologically as the unique countable metrizable space
Topological property
In topology and related areas of mathematics a topological property or topological invariant is a property of a topological space which is invariant under homeomorphisms. That is, a property of spaces is a topological property if whenever a space X possesses that property every space homeomorphic...
without isolated point
Isolated point
In topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
s.
The space is also totally disconnected
Totally disconnected space
In topology and related branches of mathematics, a totally disconnected space is a topological space that is maximally disconnected, in the sense that it has no non-trivial connected subsets...
. The rational numbers do not form a complete metric space; the real numbers are the completion of Q under the metric above.
p-adic numbers
In addition to the absolute value metric mentioned above, there are other metrics which turn Q into a topological field:Let p be a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
and for any non-zero integer a, let where pn is the highest power of p dividing
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
a.
In addition set For any rational number a/b, we set
Then defines a metric
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
on Q.
The metric space (Q,dp) is not complete, and its completion is the p-adic number field
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
Qp. Ostrowski's theorem
Ostrowski's theorem
Ostrowski's theorem, due to Alexander Ostrowski , states that any non-trivial absolute value on the rational numbers Q is equivalent to either the usual real absolute value or a p-adic absolute value.- Definitions :...
states that any non-trivial absolute value
Absolute value (algebra)
In mathematics, an absolute value is a function which measures the "size" of elements in a field or integral domain. More precisely, if D is an integral domain, then an absolute value is any mapping | x | from D to the real numbers R satisfying:* | x | ≥ 0,*...
on the rational numbers Q is equivalent to either the usual real absolute value or a p-adic
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
absolute value.