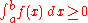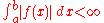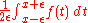Almost everywhere
Encyclopedia
In measure theory a property holds almost everywhere if the set of elements for which the property does not hold is a null set
, that is, a set of measure zero (Halmos 1974). In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero. When discussing sets of real number
s, the Lebesgue measure
is assumed unless otherwise stated.
The term almost everywhere is abbreviated a.e.; in older literature p.p. is used, to stand for the equivalent French language
phrase presque partout.
A set with full measure is one whose complement is of measure zero. In probability theory
, the terms almost surely
, almost certain and almost always refer to sets with probability
1, which are exactly the sets of full measure in a probability space.
Occasionally, instead of saying that a property holds almost everywhere, it is said that the property holds for almost all elements (though the term almost all
also has other meanings).
. An ultrafilter on a set X is a maximal collection F of subsets of X such that:
A property P of points in X holds almost everywhere, relative to an ultrafilter F, if the set of points for which P holds is in F.
For example, one construction of the hyperreal number
system defines a hyperreal number as an equivalence class of sequences that are equal almost everywhere as defined by an ultrafilter.
The definition of almost everywhere in terms of ultrafilters is closely related to the definition in terms of measures, because each ultrafilter defines a finitely-additive measure taking only the values 0 and 1, where a set has measure 1 if and only if it is included in the ultrafilter.
Null set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
, that is, a set of measure zero (Halmos 1974). In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero. When discussing sets of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
is assumed unless otherwise stated.
The term almost everywhere is abbreviated a.e.; in older literature p.p. is used, to stand for the equivalent French language
French language
French is a Romance language spoken as a first language in France, the Romandy region in Switzerland, Wallonia and Brussels in Belgium, Monaco, the regions of Quebec and Acadia in Canada, and by various communities elsewhere. Second-language speakers of French are distributed throughout many parts...
phrase presque partout.
A set with full measure is one whose complement is of measure zero. In probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the terms almost surely
Almost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
, almost certain and almost always refer to sets with probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
1, which are exactly the sets of full measure in a probability space.
Occasionally, instead of saying that a property holds almost everywhere, it is said that the property holds for almost all elements (though the term almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
also has other meanings).
Properties
- If f : R → R is a Lebesgue integrable function and f(x) ≥ 0 almost everywhere, then
- for all real numbers a < b with equality iffIFFIFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
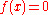 almost everywhere.
almost everywhere.
- If f : [a, b] → R is a monotonic functionMonotonic functionIn mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
, then f is differentiableDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
almost everywhere. - If f : R → R is Lebesgue measurable and
- for all real numbers a < b, then there exists a set E (depending on f) such that, if x is in E, the Lebesgue mean
- converges to f(x) as
 decreases to zero. The set E is called the Lebesgue set of f. Its complement can be proved to have measure zero. In other words, the Lebesgue mean of f converges to f almost everywhere.
decreases to zero. The set E is called the Lebesgue set of f. Its complement can be proved to have measure zero. In other words, the Lebesgue mean of f converges to f almost everywhere.
- If f(x,y) is Borel measurable on R2 then for almost every x, the function y→f(x,y) is Borel measurable.
- A bounded functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f : [a, b] -> R is Riemann integrableRiemann integralIn the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
if and only if it is continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
almost everywhere.
Definition using ultrafilters
Outside of the context of real analysis, the notion of a property true almost everywhere is sometimes defined in terms of an ultrafilterUltrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
. An ultrafilter on a set X is a maximal collection F of subsets of X such that:
- If U ∈ F and U ⊆ V then V ∈ F
- The intersection of any two sets in F is in F
- The empty set is not in F
A property P of points in X holds almost everywhere, relative to an ultrafilter F, if the set of points for which P holds is in F.
For example, one construction of the hyperreal number
Hyperreal number
The system of hyperreal numbers represents a rigorous method of treating the infinite and infinitesimal quantities. The hyperreals, or nonstandard reals, *R, are an extension of the real numbers R that contains numbers greater than anything of the form1 + 1 + \cdots + 1. \, Such a number is...
system defines a hyperreal number as an equivalence class of sequences that are equal almost everywhere as defined by an ultrafilter.
The definition of almost everywhere in terms of ultrafilters is closely related to the definition in terms of measures, because each ultrafilter defines a finitely-additive measure taking only the values 0 and 1, where a set has measure 1 if and only if it is included in the ultrafilter.