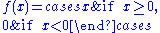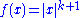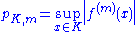Smooth function
Encyclopedia

Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, a differentiability class is a classification of functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
according to the properties of their derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.
Most of this article is about real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
-valued functions of one real variable. A discussion of the multivariable case is presented towards the end.
Differentiability classes
Consider an open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
and a function f defined on that set with real values. Let k be a non-negative integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
. The function f is said to be of class Ck if the derivatives f, f
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
(the continuity is automatic for all the derivatives except for f(k)). The function f is said to be of class C∞, or smooth, if it has derivatives of all orders. f is said to be of class Cω, or analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
, if f is smooth and if it equals its Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansion around any point in its domain.
To put it differently, the class C0 consists of all continuous functions. The class C1 consists of all differentiable function
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
s whose derivative is continuous; such functions are called continuously differentiable. Thus, a C1 function is exactly a function whose derivative exists and is of class C0. In general, the classes Ck can be defined recursively
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
by declaring C0 to be the set of all continuous functions and declaring Ck for any positive integer k to be the set of all differentiable functions whose derivative is in Ck−1. In particular, Ck is contained in Ck−1 for every k, and there are examples to show that this containment is strict. C∞ is the intersection of the sets Ck as k varies over the non-negative integers. Cω is strictly contained in C∞; for an example of this, see bump function or also below.
Examples
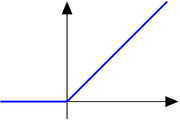
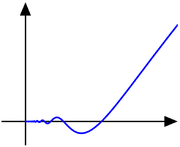
is continuous, but not differentiable at
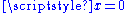 , so it is of class C0 but not of class C1.
, so it is of class C0 but not of class C1.The function

is differentiable, with derivative

Because cos(1/x) oscillates as x approaches zero, f ’(x) is not continuous at zero. Therefore, this function is differentiable but not of class C1. Moreover, if one takes f(x) = x3/2 sin(1/x) (x ≠ 0) in this example, it can be used to show that the derivative function of a differentiable function can be unbounded on a compact set and, therefore, that a differentiable function on a compact set may not be locally Lipschitz continuous.
The functions
where k is even, are continuous and k times differentiable at all x. But at
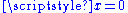 they are not (k+1) times differentiable, so they are of class C k but not of class C j where j>k.
they are not (k+1) times differentiable, so they are of class C k but not of class C j where j>k.The exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
is analytic, so, of class Cω. The trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s are also analytic wherever they are defined.
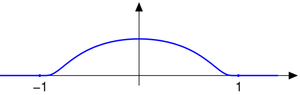
The function
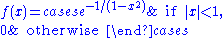
is smooth, so of class C∞, but it is not analytic at
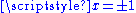 , so it is not of class Cω. The function f is an example of a smooth function with
, so it is not of class Cω. The function f is an example of a smooth function withcompact support.
Multivariate differentiability classes
Let n and m be some positive integers. If f is a function from an open subset of Rn with values in Rm, then f has component functions f1, ..., fm. Each of these may or may not have partial derivativePartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s. We say that f is of class Ck if all of the partial derivatives
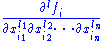 exist and are continuous, where each of
exist and are continuous, where each of  is an integer between 1 and n, each of
is an integer between 1 and n, each of 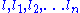 is an integer between 0 and k,
is an integer between 0 and k,  . The classes C∞ and Cω are defined as before.
. The classes C∞ and Cω are defined as before.These criteria of differentiability can be applied to the transition functions of a differential structure
Differential structure
In mathematics, an n-dimensional differential structure on a set M makes M into an n-dimensional differential manifold, which is a topological manifold with some additional structure that allows us to do differential calculus on the manifold...
. The resulting space is called a Ck manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
.
If one wishes to start with a coordinate-independent definition of the class Ck, one may start by considering maps between Banach spaces. A map from one Banach space to another is differentiable at a point if there is an affine map which approximates it at that point. The derivative of the map assigns to the point x the linear part of the affine approximation to the map at x. Since the space of linear maps from one Banach space to another is again a Banach space, we may continue this procedure to define higher order derivatives. A map f is of class Ck if it has continuous derivatives up to order k, as before.
Note that Rn is a Banach space for any value of n, so the coordinate-free approach is applicable in this instance. It can be shown that the definition in terms of partial derivatives and the coordinate-free approach are equivalent; that is, a function f is of class Ck by one definition iff it is so by the other definition.
The space of Ck functions
Let D be an open subset of the real line. The set of all Ck functions defined on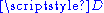 and taking real values is a Fréchet space
and taking real values is a Fréchet spaceFréchet space
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
with the countable family of seminorms
where K varies over an increasing sequence of compact sets whose union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
is D, and m = 0, 1, …, k.
The set of C∞ functions over
 also forms a Fréchet space. One uses the same seminorms as above, except that
also forms a Fréchet space. One uses the same seminorms as above, except that  is allowed to range over all non-negative integer values.
is allowed to range over all non-negative integer values.The above spaces occur naturally in applications where functions having derivatives of certain orders are necessary; however, particularly in the study of partial differential equations, it can sometimes be more fruitful to work instead with the Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s.
Parametric continuity
Parametric continuity is a concept applied to parametric curves describing the smoothness of the parameter's value with distance along the curve.Definition
A curve can be said to have Cn continuity if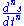
is continuous of value throughout the curve.
As an example of a practical application of this concept, a curve describing the motion of an object with a parameter of time, must have C1 continuity for the object to have finite acceleration. For smoother motion, such as that of a camera's path while making a film, higher levels of parametric continuity are required.
Order of continuity
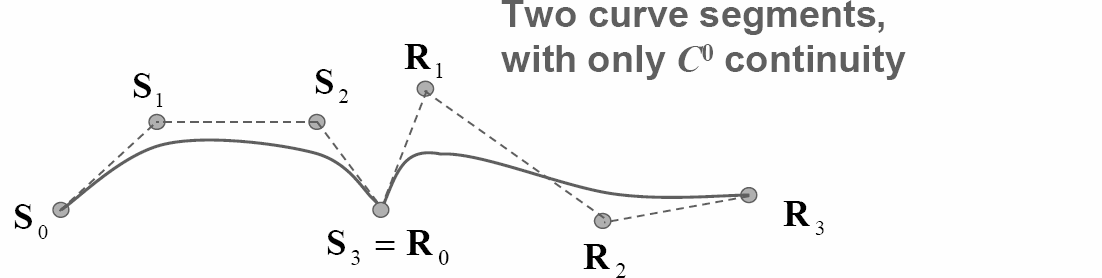
- C−1: curves include discontinuities
- C0: curves are joined
- C1: first derivatives are equal
- C2: first and second derivatives are equal
- Cn: first through nth derivatives are equal
The term parametric continuity was introduced to distinguish it from geometric continuity (Gn) which removes restrictions on the speed
Speed
In kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as...
with which the parameter traces out the curve.
Geometric continuity
The concept of geometrical or geometric continuity was primarily applied to the conic sections and related shapes by mathematicians such as LeibnizGottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
, Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
, and Poncelet
Jean-Victor Poncelet
Jean-Victor Poncelet was a French engineer and mathematician who served most notably as the commandant general of the École Polytechnique...
. The concept was an early attempt at describing, through geometry rather than algebra, the concept of continuity
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
as expressed through a parametric function.
The basic idea behind geometric continuity was that the five conic sections were really five different versions of the same shape. An ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
tends to a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
as the eccentricity
Eccentricity (mathematics)
In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
approaches zero, or to a parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
as it approaches one; and a hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
tends to a parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
as the eccentricity drops toward one; it can also tend to intersecting line
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
s. Thus, there was continuity between the conic sections. These ideas led to other concepts of continuity. For instance, if a circle and a straight line were two expressions of the same shape, perhaps a line could be thought of as a circle of infinite radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
. For such to be the case, one would have to make the line closed by allowing the point x = ∞ to be a point on the circle, and for x = +∞ and x = −∞ to be identical. Such ideas were useful in crafting the modern, algebraically defined, idea of the continuity
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
of a function and of ∞.
Smoothness of curves and surfaces
A curveCurve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
or surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
can be described as having Gn continuity, n being the increasing measure of smoothness. Consider the segments either side of a point on a curve:
- G0: The curves touch at the join point.
- G1: The curves also share a common tangentTangentIn geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
direction at the join point. - G2: The curves also share a common center of curvature at the join point.
In general, Gn continuity exists if the curves can be reparameterized to have Cn (parametric) continuity. A reparametrization of the curve is geometrically identical to the original; only the parameter is affected.
Equivalently, two vector functions
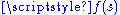 and
and  have Gn continuity if
have Gn continuity if 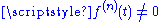 and
and 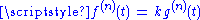 , for a scalar
, for a scalar 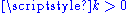 (i.e., if the direction, but not necessarily the magnitude, of the two vectors is equal).
(i.e., if the direction, but not necessarily the magnitude, of the two vectors is equal).While it may be obvious that a curve would require G1 continuity to appear smooth, for good aesthetics
Aesthetics
Aesthetics is a branch of philosophy dealing with the nature of beauty, art, and taste, and with the creation and appreciation of beauty. It is more scientifically defined as the study of sensory or sensori-emotional values, sometimes called judgments of sentiment and taste...
, such as those aspired to in architecture
Architecture
Architecture is both the process and product of planning, designing and construction. Architectural works, in the material form of buildings, are often perceived as cultural and political symbols and as works of art...
and sports car
Sports car
A sports car is a small, usually two seat, two door automobile designed for high speed driving and maneuverability....
design, higher levels of geometric continuity are required. For example, reflections in a car body will not appear smooth unless the body has G2 continuity.
A rounded rectangle (with ninety degree circular arcs at the four corners) has G1 continuity, but does not have G2 continuity. The same is true for a rounded cube, with octants of a sphere at its corners and quarter-cylinders along its edges. If an editable curve with G2 continuity is required, then cubic splines are typically chosen; these curves are frequently used in industrial design
Industrial design
Industrial design is the use of a combination of applied art and applied science to improve the aesthetics, ergonomics, and usability of a product, but it may also be used to improve the product's marketability and production...
.
Relation to analyticity
While all analytic functionAnalytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s are smooth on the set on which they are analytic, the above example shows that the converse is not true for functions on the reals: there exist smooth real functions which are not analytic. For example, the Fabius function
Fabius function
In mathematics, the Fabius function is an example of an infinitely differentiable function that is not analytic anywhere, found by .The Fabius function is defined on the unit interval, and is given by the probability distribution of...
is smooth but not analytic at any point. Although it might seem that such functions are the exception rather than the rule, it turns out that the analytic functions are scattered very thinly among the smooth ones; more rigorously, the analytic functions form a meagre
Meagre set
In the mathematical fields of general topology and descriptive set theory, a meagre set is a set that, considered as a subset of a topological space, is in a precise sense small or negligible...
subset of the smooth functions. Furthermore, for every open subset A of the real line, there exist smooth functions which are analytic on A and nowhere else.
It is useful to compare the situation to that of the ubiquity of transcendental number
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
s on the real line. Both on the real line and the set of smooth functions, the examples we come up with at first thought (algebraic/rational numbers and analytic functions) are far better behaved than the majority of cases: the transcendental numbers and nowhere analytic functions have full measure (their complements are meagre).
The situation thus described is in marked contrast to complex differentiable functions. If a complex function is differentiable just once on an open set it is both infinitely differentiable and analytic on that set.
Smooth partitions of unity
Smooth functions with given closed supportSupport (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
are used in the construction of smooth partitions of unity (see partition of unity and topology glossary
Topology glossary
This is a glossary of some terms used in the branch of mathematics known as topology. Although there is no absolute distinction between different areas of topology, the focus here is on general topology...
); these are essential in the study of smooth manifolds, for example to show that Riemannian metrics can be defined globally starting from their local existence. A simple case is that of a bump function on the real line, that is, a smooth function f that takes the value 0 outside an interval [a,b] and such that
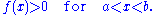
Given a number of overlapping intervals on the line, bump functions can be constructed on each of them, and on semi-infinite intervals (-∞, c] and [d,+∞) to cover the whole line, such that the sum of the functions is always 1.
From what has just been said, partitions of unity don't apply to holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s; their different behavior relative to existence and analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
is one of the roots of sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
theory. In contrast, sheaves of smooth functions tend not to carry much topological information.
Smooth functions between manifolds
Smooth maps between smooth manifolds may be defined by means of charts, since the idea of smoothness of function is independent of the particular chart used. If F is a map from an m-manifold M to an n-manifold N, then F is smooth if, for every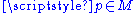 , there is a chart
, there is a chart 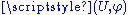 in M containing p and a chart
in M containing p and a chart 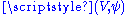 in N containing F(p) with
in N containing F(p) with 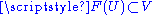 , such that
, such that  is smooth from
is smooth from 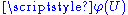 to
to 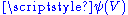 as a function from
as a function from 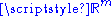 to
to  .
.Such a map has a first derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
defined on tangent vectors
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
; it gives a fibre-wise linear mapping on the level of tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
s.
Smooth functions between subsets of manifolds
There is a corresponding notion of smooth map for arbitrary subsets of manifolds. If is a function
is a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
whose domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
and range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
are subsets of manifolds
 and
and 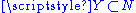 respectively.
respectively.  is said to be smooth if for all
is said to be smooth if for all 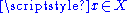 there is an open set
there is an open set 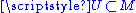 with
with 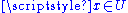 and a smooth function
and a smooth function 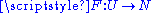 such that
such that 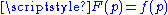 for all
for all  .
.