Riesz representation theorem
Encyclopedia
There are several well-known theorems in functional analysis
known as the Riesz representation theorem. They are named in honour of Frigyes Riesz
.
and its (continuous) dual space: if the underlying field
is the real number
s, the two are isometrically
isomorphic; if the field is the complex number
s, the two are isometrically anti-isomorphic
. The (anti-) isomorphism
is a particular natural one as will be described next.
Let
be a Hilbert space, and let 
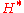denote its dual space, consisting of all continuous linear functionals from 
into the field 
or 
. If 
is an element of 
, then the function 
defined by
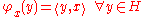
where
denotes the inner product of the Hilbert space, is an element of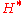 
. The Riesz representation theorem states that every element of 
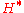can be written uniquely in this form.
Theorem. The mapping
is an isometric (anti-) isomorphism, meaning that:
The inverse map of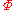
can be described as follows. Given an element 
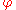of 
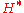, the orthogonal complement of the kernel of 
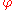is a one-dimensional subspace of 
. Take a non-zero element 
in that subspace, and set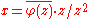 
. Then 
.
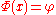Historically, the theorem is often attributed simultaneously to Riesz
and Fréchet
in 1907 (see references).
In the mathematical treatment of quantum mechanics
, the theorem can be seen as a justification for the popular bra-ket notation
. When the theorem holds, every ket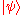
has a corresponding bra 
, and the correspondence is unambiguous.
The representation theorem for linear functionals on
The following theorem represents positive linear functionals on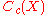 
, the space of continuous compactly
supported
complex-valued functions on a locally compact
Hausdorff space
. The Borel set
s in the following statement refer to the σ-algebra generated by the open sets.
A non-negative countably additive Borel measure
on a locally compact Hausdorff space
is regular if and only if
holds whenever
is open or when 
is Borel and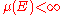 
.
Theorem. Let X be a locally compact Hausdorff space
. For any positive linear functional
ψ on Cc(X), there is a unique Borel regular measure
μ on X such that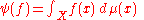
for all f in Cc(X).
One approach to measure theory is to start with a Radon measure
, defined as a positive linear functional on C(X). This is the way adopted by Bourbaki; it does of course assume that X starts life as a topological space
, rather than simply as a set. For locally compact spaces an integration theory is then recovered.
Historical remark: In its original form by F. Riesz (1909) the theorem states that every continuous linear functional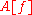
over the space C[0,1] of continuous functions in the interval [0,1] can be represented in the form
where
is a function of bounded variation
on the interval [0,1], and the integral is a Riemann-Stieltjes integral. Since there is a one-to-one correspondence between Borel regular measures in the interval and functions of bounded variation (that assigns to each function of bounded variation the corresponding Lebesgue-Stieltjes measure, and the integral with respect to the Lebesgue-Stieltjes measure agrees with the Riemann-Stieltjes integral for continuous functions ), the above stated theorem generalizes the original statement of F. Riesz.
(See Gray(1984), for a historical discussion).
The representation theorem for the dual of
The following theorem, also referred to as the Riesz-Markov theorem, gives a concrete realisation of the dual space
of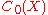
, the set of continuous function
s on
which vanish at infinity. The Borel set
s in the statement of the theorem also refers to the
-algebra generated by the open sets.
If
is a complex-valued countably additive Borel measure, 
is regular iff the non-negative countably additive measure 
is regular as defined above.
Theorem. Let
be a locally compact Hausdorff space. For any continuous linear functional
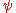on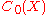 
, there is a unique regular countably additive complex Borel measure 
on 
such that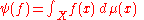
for all
in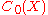 
. The norm of 
as a linear functional is the total variation
of
, that is
Finally,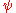
is positive
iff the measure
is non-negative.
Remark. One might expect that by the Hahn-Banach theorem
for bounded linear functionals, every bounded linear functional on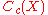
extends in exactly one way to a bounded linear functional on 
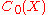, the latter being the closure
of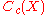
in the supremum norm, and that for this reason the first statement implies the second. However the first result is for positive linear functionals, not bounded linear functionals, so the two facts are not in fact equivalent. There is also the fact that the measure in the first case is much more restricted than the measure in the second.
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
known as the Riesz representation theorem. They are named in honour of Frigyes Riesz
Frigyes Riesz
Frigyes Riesz was a mathematician who was born in Győr, Hungary and died in Budapest, Hungary. He was rector and professor at University of Szeged...
.
The Hilbert space representation theorem
This theorem establishes an important connection between a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
and its (continuous) dual space: if the underlying field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
is the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, the two are isometrically
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
isomorphic; if the field is the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, the two are isometrically anti-isomorphic
Antiisomorphic
In modern algebra, an antiisomorphism between structured sets A and B is an isomorphism from A to the opposite of B...
. The (anti-) isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
is a particular natural one as will be described next.
Let
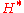be a Hilbert space, and let denote its dual space, consisting of all continuous linear functionals from into the field or . If is an element of , then the function defined by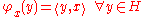where
denotes the inner product of the Hilbert space, is an element of 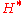. The Riesz representation theorem states that every element of 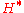can be written uniquely in this form.Theorem. The mapping
is an isometric (anti-) isomorphism, meaning that:
-
is bijective. - The norms of
and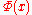 
agree: 
. -
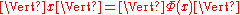is additive: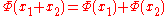 
. - If the base field is
, then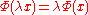 
for all real numbers 
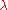. - If the base field is
, then 
for all complex numbers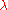 
, where 
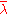denotes the complex conjugation of 
.
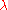The inverse map of
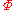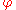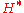can be described as follows. Given an element of , the orthogonal complement of the kernel of 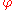is a one-dimensional subspace of . Take a non-zero element in that subspace, and set 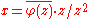. Then 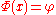.Historically, the theorem is often attributed simultaneously to Riesz
Frigyes Riesz
Frigyes Riesz was a mathematician who was born in Győr, Hungary and died in Budapest, Hungary. He was rector and professor at University of Szeged...
and Fréchet
Maurice René Fréchet
Maurice Fréchet was a French mathematician. He made major contributions to the topology of point sets and introduced the entire concept of metric spaces. He also made several important contributions to the field of statistics and probability, as well as calculus...
in 1907 (see references).
In the mathematical treatment of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the theorem can be seen as a justification for the popular bra-ket notation
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
. When the theorem holds, every ket
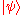has a corresponding bra , and the correspondence is unambiguous. The representation theorem for linear functionals on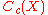 
The following theorem represents positive linear functionals on 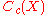, the space of continuous compactlyCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
supported
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
complex-valued functions on a locally compact
Locally compact space
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
. The Borel setBorel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
s in the following statement refer to the σ-algebra generated by the open sets.
A non-negative countably additive Borel measure
on a locally compact Hausdorff spaceHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
is regular if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
-
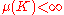for every compact 
;
- For every Borel set
,
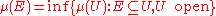
- The relation
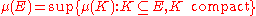
holds whenever
is open or when is Borel and 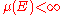.Theorem. Let X be a locally compact Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
. For any positive linear functional
Positive linear functional
In mathematics, especially in functional analysis, a positive linear functional on an ordered vector space is a linear functional f on V so that for all positive elements v of V, that is v≥0, it holds thatf\geq 0....
ψ on Cc(X), there is a unique Borel regular measure
Borel regular measure
In mathematics, an outer measure μ on n-dimensional Euclidean space Rn is called Borel regular if the following two conditions hold:...
μ on X such that
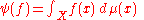
for all f in Cc(X).
One approach to measure theory is to start with a Radon measure
Radon measure
In mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
, defined as a positive linear functional on C(X). This is the way adopted by Bourbaki; it does of course assume that X starts life as a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, rather than simply as a set. For locally compact spaces an integration theory is then recovered.
Historical remark: In its original form by F. Riesz (1909) the theorem states that every continuous linear functional
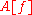over the space C[0,1] of continuous functions in the interval [0,1] can be represented in the formwhere
is a function of bounded variationBounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
on the interval [0,1], and the integral is a Riemann-Stieltjes integral. Since there is a one-to-one correspondence between Borel regular measures in the interval and functions of bounded variation (that assigns to each function of bounded variation the corresponding Lebesgue-Stieltjes measure, and the integral with respect to the Lebesgue-Stieltjes measure agrees with the Riemann-Stieltjes integral for continuous functions ), the above stated theorem generalizes the original statement of F. Riesz.
(See Gray(1984), for a historical discussion).
The representation theorem for the dual of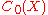 
The following theorem, also referred to as the Riesz-Markov theorem, gives a concrete realisation of the dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of
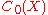, the set of continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s on
which vanish at infinity. The Borel setBorel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
s in the statement of the theorem also refers to the
-algebra generated by the open sets.If
is a complex-valued countably additive Borel measure, is regular iff the non-negative countably additive measure is regular as defined above.Theorem. Let
be a locally compact Hausdorff space. For any continuous linear functionalLinear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
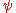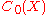on , there is a unique regular countably additive complex Borel measure on such that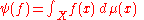for all
in 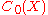. The norm of as a linear functional is the total variationTotal variation
In mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
of
, that isFinally,
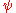is positivePositive linear functional
In mathematics, especially in functional analysis, a positive linear functional on an ordered vector space is a linear functional f on V so that for all positive elements v of V, that is v≥0, it holds thatf\geq 0....
iff the measure
is non-negative.Remark. One might expect that by the Hahn-Banach theorem
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
for bounded linear functionals, every bounded linear functional on
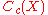extends in exactly one way to a bounded linear functional on 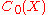, the latter being the closureClosure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of
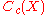in the supremum norm, and that for this reason the first statement implies the second. However the first result is for positive linear functionals, not bounded linear functionals, so the two facts are not in fact equivalent. There is also the fact that the measure in the first case is much more restricted than the measure in the second.