Discrete cosine transform
Encyclopedia
A discrete cosine transform (DCT) expresses a sequence of finitely many data points in terms of a sum of cosine functions oscillating at different frequencies
. DCTs are important to numerous applications in science and engineering, from lossy compression of audio (e.g. MP3
) and images
(e.g. JPEG
) (where small high-frequency components can be discarded), to spectral method
s for the numerical solution of partial differential equations. The use of cosine rather than sine
functions is critical in these applications: for compression, it turns out that cosine functions are much more efficient (as described below, fewer are needed to approximate a typical signal
), whereas for differential equations the cosines express a particular choice of boundary conditions.
In particular, a DCT is a Fourier-related transform similar to the discrete Fourier transform
(DFT), but using only real number
s. DCTs are equivalent to DFTs of roughly twice the length, operating on real data with even
symmetry (since the Fourier transform of a real and even function is real and even), where in some variants the input and/or output data are shifted by half a sample. There are eight standard DCT variants, of which four are common.
The most common variant of discrete cosine transform is the type-II DCT, which is often called simply "the DCT"; its inverse, the type-III DCT, is correspondingly often called simply "the inverse DCT" or "the IDCT". Two related transforms are the discrete sine transform
(DST), which is equivalent to a DFT of real and odd functions, and the modified discrete cosine transform
(MDCT), which is based on a DCT of overlapping data.
es. As explained below, this stems from the boundary conditions implicit in the cosine functions.
A related transform, the modified discrete cosine transform
, or MDCT (based on the DCT-IV), is used in AAC
, Vorbis
, WMA
, and MP3
audio compression.
DCTs are also widely employed in solving partial differential equations by spectral methods, where the different variants of the DCT correspond to slightly different even/odd boundary conditions at the two ends of the array.
DCTs are also closely related to Chebyshev polynomials
, and fast DCT algorithms (below) are used in Chebyshev approximation of arbitrary functions by series of Chebyshev polynomials, for example in Clenshaw–Curtis quadrature.
image compression, MJPEG
, MPEG, DV
, and Theora
video compression. There, the two-dimensional DCT-II of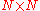
blocks are computed and the results are quantized
and entropy coded
. In this case,
is typically 8 and the DCT-II formula is applied to each row and column of the block. The result is an 8 × 8 transform coefficient array in which the 
element (top-left) is the DC (zero-frequency) component and entries with increasing vertical and horizontal index values represent higher vertical and horizontal spatial frequencies.
with different frequencies and amplitude
s. Like the discrete Fourier transform
(DFT), a DCT operates on a function at a finite number of discrete data points. The obvious distinction between a DCT and a DFT is that the former uses only cosine functions, while the latter uses both cosines and sines (in the form of complex exponentials). However, this visible difference is merely a consequence of a deeper distinction: a DCT implies different boundary conditions than the DFT or other related transforms.
The Fourier-related transforms that operate on a function over a finite domain
, such as the DFT or DCT or a Fourier series
, can be thought of as implicitly defining an extension of that function outside the domain. That is, once you write a function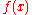
as a sum of sinusoids, you can evaluate that sum at any 
, even for 
where the original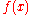 
was not specified. The DFT, like the Fourier series, implies a periodic
extension of the original function. A DCT, like a cosine transform
, implies an even
extension of the original function.
However, because DCTs operate on finite, discrete sequences, two issues arise that do not apply for the continuous cosine transform. First, one has to specify whether the function is even or odd at both the left and right boundaries of the domain (i.e. the min-n and max-n boundaries in the definitions below, respectively). Second, one has to specify around what point the function is even or odd. In particular, consider a sequence abcd of four equally spaced data points, and say that we specify an even left boundary. There are two sensible possibilities: either the data is even about the sample a, in which case the even extension is dcbabcd, or the data is even about the point halfway between a and the previous point, in which case the even extension is dcbaabcd (a is repeated).
These choices lead to all the standard variations of DCTs and also discrete sine transform
s (DSTs).
Each boundary can be either even or odd (2 choices per boundary) and can be symmetric about a data point or the point halfway between two data points (2 choices per boundary), for a total of 2 × 2 × 2 × 2 = 16 possibilities. Half of these possibilities, those where the left boundary is even, correspond to the 8 types of DCT; the other half are the 8 types of DST.
These different boundary conditions strongly affect the applications of the transform, and lead to uniquely useful properties for the various DCT types. Most directly, when using Fourier-related transforms to solve partial differential equation
s by spectral method
s, the boundary conditions are directly specified as a part of the problem being solved. Or, for the MDCT
(based on the type-IV DCT), the boundary conditions are intimately involved in the MDCT's critical property of time-domain aliasing cancellation. In a more subtle fashion, the boundary conditions are responsible for the "energy compaction" properties that make DCTs useful for image and audio compression, because the boundaries affect the rate of convergence of any Fourier-like series.
In particular, it is well known that any discontinuities
in a function reduce the rate of convergence
of the Fourier series, so that more sinusoids are needed to represent the function with a given accuracy. The same principle governs the usefulness of the DFT and other transforms for signal compression: the smoother a function is, the fewer terms in its DFT or DCT are required to represent it accurately, and the more it can be compressed. (Here, we think of the DFT or DCT as approximations for the Fourier series
or cosine series of a function, respectively, in order to talk about its "smoothness".) However, the implicit periodicity of the DFT means that discontinuities usually occur at the boundaries: any random segment of a signal is unlikely to have the same value at both the left and right boundaries. (A similar problem arises for the DST, in which the odd left boundary condition implies a discontinuity for any function that does not happen to be zero at that boundary.) In contrast, a DCT where both boundaries are even always yields a continuous extension at the boundaries (although the slope
is generally discontinuous). This is why DCTs, and in particular DCTs of types I, II, V, and VI (the types that have two even boundaries) generally perform better for signal compression than DFTs and DSTs. In practice, a type-II DCT is usually preferred for such applications, in part for reasons of computational convenience.
, invertible function
F : RN -> RN (where R denotes the set of real number
s), or equivalently an invertible N × N square matrix. There are several variants of the DCT with slightly modified definitions. The N real numbers x0, ..., xN-1 are transformed into the N real numbers X0, ..., XN-1 according to one of the formulas:
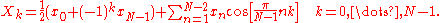
Some authors further multiply the x0 and xN-1 terms by √2, and correspondingly multiply the X0 and XN-1 terms by 1/√2. This makes the DCT-I matrix orthogonal
, if one further multiplies by an overall scale factor of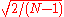
, but breaks the direct correspondence with a real-even DFT.
The DCT-I is exactly equivalent (up to an overall scale factor of 2), to a DFT of
real numbers with even symmetry. For example, a DCT-I of N=5 real numbers abcde is exactly equivalent to a DFT of eight real numbers abcdedcb (even symmetry), divided by two. (In contrast, DCT types II-IV involve a half-sample shift in the equivalent DFT.)
Note, however, that the DCT-I is not defined for N less than 2. (All other DCT types are defined for any positive N.)
Thus, the DCT-I corresponds to the boundary conditions: xn is even around n=0 and even around n=N-1; similarly for Xk.
The DCT-II is probably the most commonly used form, and is often simply referred to as "the DCT".
This transform is exactly equivalent (up to an overall scale factor of 2) to a DFT of
real inputs of even symmetry where the even-indexed elements are zero. That is, it is half of the DFT of the 
inputs 
, where 
, 
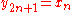for 
, and 
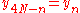for 
.
Some authors further multiply the X0 term by 1/√2 and multiply the resulting matrix by an overall scale factor of
(see below for the corresponding change in DCT-III). This makes the DCT-II matrix orthogonal
, but breaks the direct correspondence with a real-even DFT of half-shifted input.
The DCT-II implies the boundary conditions: xn is even around n=-1/2 and even around n=N-1/2; Xk is even around k=0 and odd around k=N.
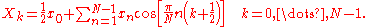
Because it is the inverse of DCT-II (up to a scale factor, see below), this form is sometimes simply referred to as "the inverse DCT" ("IDCT").
Some authors further multiply the x0 term by √2 and multiply the resulting matrix by an overall scale factor of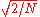
(see above for the corresponding change in DCT-II), so that the DCT-II and DCT-III are transposes of one another. This makes the DCT-III matrix orthogonal
, but breaks the direct correspondence with a real-even DFT of half-shifted output.
The DCT-III implies the boundary conditions: xn is even around n=0 and odd around n=N; Xk is even around k=-1/2 and even around k=N-1/2.
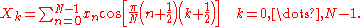
The DCT-IV matrix becomes orthogonal
(and thus, being clearly symmetric, its own inverse) if one further multiplies by an overall scale factor of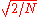
.
A variant of the DCT-IV, where data from different transforms are overlapped, is called the modified discrete cosine transform
(MDCT) (Malvar, 1992).
The DCT-IV implies the boundary conditions: xn is even around n=-1/2 and odd around n=N-1/2; similarly for Xk.
Equivalently, DCTs of types I-IV imply boundaries that are even/odd around either a data point for both boundaries or halfway between two data points for both boundaries. DCTs of types V-VIII imply boundaries that even/odd around a data point for one boundary and halfway between two data points for the other boundary.
However, these variants seem to be rarely used in practice. One reason, perhaps, is that FFT algorithms for odd-length DFTs are generally more complicated than FFT algorithms for even-length DFTs (e.g. the simplest radix-2 algorithms are only for even lengths), and this increased intricacy carries over to the DCTs as described below.
(The trivial real-even array, a length-one DFT (odd length) of a single number a, corresponds to a DCT-V of length N=1.)
Like for the DFT
, the normalization factor in front of these transform definitions is merely a convention and differs between treatments. For example, some authors multiply the transforms by
so that the inverse does not require any additional multiplicative factor. Combined with appropriate factors of √2 (see above), this can be used to make the transform matrix orthogonal
.
For example, a two-dimensional DCT-II of an image or a matrix is simply the one-dimensional DCT-II, from above, performed along the rows and then along the columns (or vice versa). That is, the 2d DCT-II is given by the formula (omitting normalization and other scale factors, as above):
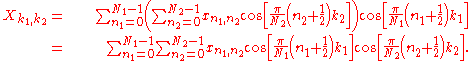
Technically, computing a two- (or multi-) dimensional DCT by sequences of one-dimensional DCTs along each dimension is known as a row-column algorithm (after the two-dimensional case). As with multidimensional FFT algorithms, however, there exist other methods to compute the same thing while performing the computations in a different order (i.e. interleaving/combining the algorithms for the different dimensions).
The inverse of a multi-dimensional DCT is just a separable product of the inverse(s) of the corresponding one-dimensional DCT(s) (see above), e.g. the one-dimensional inverses applied along one dimension at a time in a row-column algorithm.
The image to the right shows combination of horizontal and vertical frequencies for an 8 x 8 (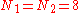
) two-dimensional DCT.
Each step from left to right and top to bottom is an increase in frequency by 1/2 cycle.
For example, moving right one from the top-left square yields a half-cycle increase in the horizontal frequency. Another move to the right yields two half-cycles. A move down yields two half-cycles horizontally and a half-cycle vertically. The source data (8x8) is transformed to a linear combination
of these 64 frequency squares.
(FFT). One can also compute DCTs via FFTs combined with O(N) pre- and post-processing steps. In general, O(N log N) methods to compute DCTs are known as fast cosine transform (FCT) algorithms.
The most efficient algorithms, in principle, are usually those that are specialized directly for the DCT, as opposed to using an ordinary FFT plus O(N) extra operations (see below for an exception). However, even "specialized" DCT algorithms (including all of those that achieve the lowest known arithmetic counts, at least for power-of-two
sizes) are typically closely related to FFT algorithms—since DCTs are essentially DFTs of real-even data, one can design a fast DCT algorithm by taking an FFT and eliminating the redundant operations due to this symmetry. This can even be done automatically (Frigo & Johnson, 2005). Algorithms based on the Cooley–Tukey FFT algorithm are most common, but any other FFT algorithm is also applicable. For example, the Winograd FFT algorithm leads to minimal-multiplication algorithms for the DFT, albeit generally at the cost of more additions, and a similar algorithm was proposed by Feig & Winograd (1992) for the DCT. Because the algorithms for DFTs, DCTs, and similar transforms are all so closely related, any improvement in algorithms for one transform will theoretically lead to immediate gains for the other transforms as well (Duhamel & Vetterli, 1990).
While DCT algorithms that employ an unmodified FFT often have some theoretical overhead compared to the best specialized DCT algorithms, the former also have a distinct advantage: highly optimized FFT programs are widely available. Thus, in practice, it is often easier to obtain high performance for general lengths N with FFT-based algorithms. (Performance on modern hardware is typically not dominated simply by arithmetic counts, and optimization requires substantial engineering effort.) Specialized DCT algorithms, on the other hand, see widespread use for transforms of small, fixed sizes such as the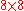
DCT-II used in JPEG
compression, or the small DCTs (or MDCTs) typically used in audio compression. (Reduced code size may also be a reason to use a specialized DCT for embedded-device applications.)
In fact, even the DCT algorithms using an ordinary FFT are sometimes equivalent to pruning the redundant operations from a larger FFT of real-symmetric data, and they can even be optimal from the perspective of arithmetic counts. For example, a type-II DCT is equivalent to a DFT of size
with real-even symmetry whose even-indexed elements are zero. One of the most common methods for computing this via an FFT (e.g. the method used in FFTPACK
and FFTW
) was described by Narasimha & Peterson (1978) and Makhoul (1980), and this method in hindsight can be seen as one step of a radix-4 decimation-in-time Cooley–Tukey algorithm applied to the "logical" real-even DFT corresponding to the DCT II. (The radix-4 step reduces the size
DFT to four size-
DFTs of real data, two of which are zero and two of which are equal to one another by the even symmetry, hence giving a single size-
FFT of real data plus 
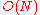butterflies.) Because the even-indexed elements are zero, this radix-4 step is exactly the same as a split-radix step; if the subsequent size-
real-data FFT is also performed by a real-data split-radix algorithm
(as in Sorensen et al., 1987), then the resulting algorithm actually matches what was long the lowest published arithmetic count for the power-of-two DCT-II (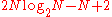
real-arithmetic operations). So, there is nothing intrinsically bad about computing the DCT via an FFT from an arithmetic perspective—it is sometimes merely a question of whether the corresponding FFT algorithm is optimal. (As a practical matter, the function-call overhead in invoking a separate FFT routine might be significant for small 
, but this is an implementation rather than an algorithmic question since it can be solved by unrolling/inlining.)
DCT of the image.
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
. DCTs are important to numerous applications in science and engineering, from lossy compression of audio (e.g. MP3
MP3
MPEG-1 or MPEG-2 Audio Layer III, more commonly referred to as MP3, is a patented digital audio encoding format using a form of lossy data compression...
) and images
Image compression
The objective of image compression is to reduce irrelevance and redundancy of the image data in order to be able to store or transmit data in an efficient form.- Lossy and lossless compression :...
(e.g. JPEG
JPEG
In computing, JPEG . The degree of compression can be adjusted, allowing a selectable tradeoff between storage size and image quality. JPEG typically achieves 10:1 compression with little perceptible loss in image quality....
) (where small high-frequency components can be discarded), to spectral method
Spectral method
Spectral methods are a class of techniques used in applied mathematics and scientific computing to numerically solve certain Dynamical Systems, often involving the use of the Fast Fourier Transform. Where applicable, spectral methods have excellent error properties, with the so called "exponential...
s for the numerical solution of partial differential equations. The use of cosine rather than sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
functions is critical in these applications: for compression, it turns out that cosine functions are much more efficient (as described below, fewer are needed to approximate a typical signal
Signal (electrical engineering)
In the fields of communications, signal processing, and in electrical engineering more generally, a signal is any time-varying or spatial-varying quantity....
), whereas for differential equations the cosines express a particular choice of boundary conditions.
In particular, a DCT is a Fourier-related transform similar to the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
(DFT), but using only real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. DCTs are equivalent to DFTs of roughly twice the length, operating on real data with even
Even and odd functions
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series...
symmetry (since the Fourier transform of a real and even function is real and even), where in some variants the input and/or output data are shifted by half a sample. There are eight standard DCT variants, of which four are common.
The most common variant of discrete cosine transform is the type-II DCT, which is often called simply "the DCT"; its inverse, the type-III DCT, is correspondingly often called simply "the inverse DCT" or "the IDCT". Two related transforms are the discrete sine transform
Discrete sine transform
In mathematics, the discrete sine transform is a Fourier-related transform similar to the discrete Fourier transform , but using a purely real matrix...
(DST), which is equivalent to a DFT of real and odd functions, and the modified discrete cosine transform
Modified discrete cosine transform
The modified discrete cosine transform is a Fourier-related transform based on the type-IV discrete cosine transform , with the additional property of being lapped: it is designed to be performed on consecutive blocks of a larger dataset,...
(MDCT), which is based on a DCT of overlapping data.
Applications
The DCT, and in particular the DCT-II, is often used in signal and image processing, especially for lossy data compression, because it has a strong "energy compaction" property (Rao and Yip, 1990): most of the signal information tends to be concentrated in a few low-frequency components of the DCT, approaching the Karhunen-Loève transform (which is optimal in the decorrelation sense) for signals based on certain limits of Markov processMarkov process
In probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
es. As explained below, this stems from the boundary conditions implicit in the cosine functions.
A related transform, the modified discrete cosine transform
Modified discrete cosine transform
The modified discrete cosine transform is a Fourier-related transform based on the type-IV discrete cosine transform , with the additional property of being lapped: it is designed to be performed on consecutive blocks of a larger dataset,...
, or MDCT (based on the DCT-IV), is used in AAC
Advanced Audio Coding
Advanced Audio Coding is a standardized, lossy compression and encoding scheme for digital audio. Designed to be the successor of the MP3 format, AAC generally achieves better sound quality than MP3 at similar bit rates....
, Vorbis
Vorbis
Vorbis is a free software / open source project headed by the Xiph.Org Foundation . The project produces an audio format specification and software implementation for lossy audio compression...
, WMA
Windows Media Audio
Windows Media Audio is an audio data compression technology developed by Microsoft. The name can be used to refer to its audio file format or its audio codecs. It is a proprietary technology that forms part of the Windows Media framework. WMA consists of four distinct codecs...
, and MP3
MP3
MPEG-1 or MPEG-2 Audio Layer III, more commonly referred to as MP3, is a patented digital audio encoding format using a form of lossy data compression...
audio compression.
DCTs are also widely employed in solving partial differential equations by spectral methods, where the different variants of the DCT correspond to slightly different even/odd boundary conditions at the two ends of the array.
DCTs are also closely related to Chebyshev polynomials
Chebyshev polynomials
In mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
, and fast DCT algorithms (below) are used in Chebyshev approximation of arbitrary functions by series of Chebyshev polynomials, for example in Clenshaw–Curtis quadrature.
JPEG
The DCT is used in JPEGJPEG
In computing, JPEG . The degree of compression can be adjusted, allowing a selectable tradeoff between storage size and image quality. JPEG typically achieves 10:1 compression with little perceptible loss in image quality....
image compression, MJPEG
MJPEG
In multimedia, Motion JPEG is an informal name for a class of video formats where each video frame or interlaced field of a digital video sequence is separately compressed as a JPEG image...
, MPEG, DV
DV
DV is a format for the digital recording and playing back of digital video. The DV codec was launched in 1995 with joint efforts of leading producers of video camcorders....
, and Theora
Theora
Theora is a free lossy video compression format. It is developed by the Xiph.Org Foundation and distributed without licensing fees alongside their other free and open media projects, including the Vorbis audio format and the Ogg container....
video compression. There, the two-dimensional DCT-II of
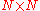blocks are computed and the results are quantizedQuantization (signal processing)
Quantization, in mathematics and digital signal processing, is the process of mapping a large set of input values to a smaller set – such as rounding values to some unit of precision. A device or algorithmic function that performs quantization is called a quantizer. The error introduced by...
and entropy coded
Entropy encoding
In information theory an entropy encoding is a lossless data compression scheme that is independent of the specific characteristics of the medium....
. In this case,
is typically 8 and the DCT-II formula is applied to each row and column of the block. The result is an 8 × 8 transform coefficient array in which the element (top-left) is the DC (zero-frequency) component and entries with increasing vertical and horizontal index values represent higher vertical and horizontal spatial frequencies.Informal overview
Like any Fourier-related transform, discrete cosine transforms (DCTs) express a function or a signal in terms of a sum of sinusoidsTrigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
with different frequencies and amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
s. Like the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
(DFT), a DCT operates on a function at a finite number of discrete data points. The obvious distinction between a DCT and a DFT is that the former uses only cosine functions, while the latter uses both cosines and sines (in the form of complex exponentials). However, this visible difference is merely a consequence of a deeper distinction: a DCT implies different boundary conditions than the DFT or other related transforms.
The Fourier-related transforms that operate on a function over a finite domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
, such as the DFT or DCT or a Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
, can be thought of as implicitly defining an extension of that function outside the domain. That is, once you write a function
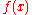as a sum of sinusoids, you can evaluate that sum at any , even for where the original 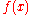was not specified. The DFT, like the Fourier series, implies a periodicPeriodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
extension of the original function. A DCT, like a cosine transform
Sine and cosine transforms
In mathematics, the Fourier sine and cosine transforms are special cases of thecontinuous Fourier transform, arising naturally when attempting to transform odd and even functions, respectively.The general Fourier transform is defined as:...
, implies an even
Even and odd functions
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series...
extension of the original function.
However, because DCTs operate on finite, discrete sequences, two issues arise that do not apply for the continuous cosine transform. First, one has to specify whether the function is even or odd at both the left and right boundaries of the domain (i.e. the min-n and max-n boundaries in the definitions below, respectively). Second, one has to specify around what point the function is even or odd. In particular, consider a sequence abcd of four equally spaced data points, and say that we specify an even left boundary. There are two sensible possibilities: either the data is even about the sample a, in which case the even extension is dcbabcd, or the data is even about the point halfway between a and the previous point, in which case the even extension is dcbaabcd (a is repeated).
These choices lead to all the standard variations of DCTs and also discrete sine transform
Discrete sine transform
In mathematics, the discrete sine transform is a Fourier-related transform similar to the discrete Fourier transform , but using a purely real matrix...
s (DSTs).
Each boundary can be either even or odd (2 choices per boundary) and can be symmetric about a data point or the point halfway between two data points (2 choices per boundary), for a total of 2 × 2 × 2 × 2 = 16 possibilities. Half of these possibilities, those where the left boundary is even, correspond to the 8 types of DCT; the other half are the 8 types of DST.
These different boundary conditions strongly affect the applications of the transform, and lead to uniquely useful properties for the various DCT types. Most directly, when using Fourier-related transforms to solve partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s by spectral method
Spectral method
Spectral methods are a class of techniques used in applied mathematics and scientific computing to numerically solve certain Dynamical Systems, often involving the use of the Fast Fourier Transform. Where applicable, spectral methods have excellent error properties, with the so called "exponential...
s, the boundary conditions are directly specified as a part of the problem being solved. Or, for the MDCT
Modified discrete cosine transform
The modified discrete cosine transform is a Fourier-related transform based on the type-IV discrete cosine transform , with the additional property of being lapped: it is designed to be performed on consecutive blocks of a larger dataset,...
(based on the type-IV DCT), the boundary conditions are intimately involved in the MDCT's critical property of time-domain aliasing cancellation. In a more subtle fashion, the boundary conditions are responsible for the "energy compaction" properties that make DCTs useful for image and audio compression, because the boundaries affect the rate of convergence of any Fourier-like series.
In particular, it is well known that any discontinuities
Classification of discontinuities
Continuous functions are of utmost importance in mathematics and applications. However, not all functions are continuous. If a function is not continuous at a point in its domain, one says that it has a discontinuity there...
in a function reduce the rate of convergence
Rate of convergence
In numerical analysis, the speed at which a convergent sequence approaches its limit is called the rate of convergence. Although strictly speaking, a limit does not give information about any finite first part of the sequence, this concept is of practical importance if we deal with a sequence of...
of the Fourier series, so that more sinusoids are needed to represent the function with a given accuracy. The same principle governs the usefulness of the DFT and other transforms for signal compression: the smoother a function is, the fewer terms in its DFT or DCT are required to represent it accurately, and the more it can be compressed. (Here, we think of the DFT or DCT as approximations for the Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
or cosine series of a function, respectively, in order to talk about its "smoothness".) However, the implicit periodicity of the DFT means that discontinuities usually occur at the boundaries: any random segment of a signal is unlikely to have the same value at both the left and right boundaries. (A similar problem arises for the DST, in which the odd left boundary condition implies a discontinuity for any function that does not happen to be zero at that boundary.) In contrast, a DCT where both boundaries are even always yields a continuous extension at the boundaries (although the slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
is generally discontinuous). This is why DCTs, and in particular DCTs of types I, II, V, and VI (the types that have two even boundaries) generally perform better for signal compression than DFTs and DSTs. In practice, a type-II DCT is usually preferred for such applications, in part for reasons of computational convenience.
Formal definition
Formally, the discrete cosine transform is a linearLinear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
, invertible function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
F : RN -> RN (where R denotes the set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s), or equivalently an invertible N × N square matrix. There are several variants of the DCT with slightly modified definitions. The N real numbers x0, ..., xN-1 are transformed into the N real numbers X0, ..., XN-1 according to one of the formulas:
DCT-I
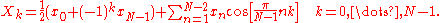
Some authors further multiply the x0 and xN-1 terms by √2, and correspondingly multiply the X0 and XN-1 terms by 1/√2. This makes the DCT-I matrix orthogonal
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
, if one further multiplies by an overall scale factor of
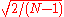, but breaks the direct correspondence with a real-even DFT.The DCT-I is exactly equivalent (up to an overall scale factor of 2), to a DFT of
real numbers with even symmetry. For example, a DCT-I of N=5 real numbers abcde is exactly equivalent to a DFT of eight real numbers abcdedcb (even symmetry), divided by two. (In contrast, DCT types II-IV involve a half-sample shift in the equivalent DFT.)Note, however, that the DCT-I is not defined for N less than 2. (All other DCT types are defined for any positive N.)
Thus, the DCT-I corresponds to the boundary conditions: xn is even around n=0 and even around n=N-1; similarly for Xk.
DCT-II
The DCT-II is probably the most commonly used form, and is often simply referred to as "the DCT".
This transform is exactly equivalent (up to an overall scale factor of 2) to a DFT of
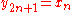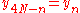real inputs of even symmetry where the even-indexed elements are zero. That is, it is half of the DFT of the inputs , where , for , and for .Some authors further multiply the X0 term by 1/√2 and multiply the resulting matrix by an overall scale factor of
(see below for the corresponding change in DCT-III). This makes the DCT-II matrix orthogonalOrthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
, but breaks the direct correspondence with a real-even DFT of half-shifted input.
The DCT-II implies the boundary conditions: xn is even around n=-1/2 and even around n=N-1/2; Xk is even around k=0 and odd around k=N.
DCT-III
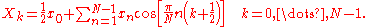
Because it is the inverse of DCT-II (up to a scale factor, see below), this form is sometimes simply referred to as "the inverse DCT" ("IDCT").
Some authors further multiply the x0 term by √2 and multiply the resulting matrix by an overall scale factor of
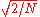(see above for the corresponding change in DCT-II), so that the DCT-II and DCT-III are transposes of one another. This makes the DCT-III matrix orthogonalOrthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
, but breaks the direct correspondence with a real-even DFT of half-shifted output.
The DCT-III implies the boundary conditions: xn is even around n=0 and odd around n=N; Xk is even around k=-1/2 and even around k=N-1/2.
DCT-IV
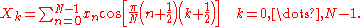
The DCT-IV matrix becomes orthogonal
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
(and thus, being clearly symmetric, its own inverse) if one further multiplies by an overall scale factor of
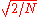.A variant of the DCT-IV, where data from different transforms are overlapped, is called the modified discrete cosine transform
Modified discrete cosine transform
The modified discrete cosine transform is a Fourier-related transform based on the type-IV discrete cosine transform , with the additional property of being lapped: it is designed to be performed on consecutive blocks of a larger dataset,...
(MDCT) (Malvar, 1992).
The DCT-IV implies the boundary conditions: xn is even around n=-1/2 and odd around n=N-1/2; similarly for Xk.
DCT V-VIII
DCT types I-IV are equivalent to real-even DFTs of even order (regardless of whether N is even or odd), since the corresponding DFT is of length 2(N−1) (for DCT-I) or 4N (for DCT-II/III) or 8N (for DCT-VIII). In principle, there are actually four additional types of discrete cosine transform (Martucci, 1994), corresponding essentially to real-even DFTs of logically odd order, which have factors of N±½ in the denominators of the cosine arguments.Equivalently, DCTs of types I-IV imply boundaries that are even/odd around either a data point for both boundaries or halfway between two data points for both boundaries. DCTs of types V-VIII imply boundaries that even/odd around a data point for one boundary and halfway between two data points for the other boundary.
However, these variants seem to be rarely used in practice. One reason, perhaps, is that FFT algorithms for odd-length DFTs are generally more complicated than FFT algorithms for even-length DFTs (e.g. the simplest radix-2 algorithms are only for even lengths), and this increased intricacy carries over to the DCTs as described below.
(The trivial real-even array, a length-one DFT (odd length) of a single number a, corresponds to a DCT-V of length N=1.)
Inverse transforms
Using the normalization conventions above, the inverse of DCT-I is DCT-I multiplied by 2/(N-1). The inverse of DCT-IV is DCT-IV multiplied by 2/N. The inverse of DCT-II is DCT-III multiplied by 2/N and vice versa. (See e.g. Rao & Yip, 1990.)Like for the DFT
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
, the normalization factor in front of these transform definitions is merely a convention and differs between treatments. For example, some authors multiply the transforms by
so that the inverse does not require any additional multiplicative factor. Combined with appropriate factors of √2 (see above), this can be used to make the transform matrix orthogonalOrthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
.
Multidimensional DCTs
Multidimensional variants of the various DCT types follow straightforwardly from the one-dimensional definitions: they are simply a separable product (equivalently, a composition) of DCTs along each dimension.For example, a two-dimensional DCT-II of an image or a matrix is simply the one-dimensional DCT-II, from above, performed along the rows and then along the columns (or vice versa). That is, the 2d DCT-II is given by the formula (omitting normalization and other scale factors, as above):
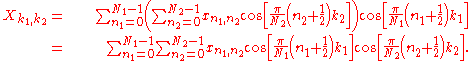
The inverse of a multi-dimensional DCT is just a separable product of the inverse(s) of the corresponding one-dimensional DCT(s) (see above), e.g. the one-dimensional inverses applied along one dimension at a time in a row-column algorithm.
The image to the right shows combination of horizontal and vertical frequencies for an 8 x 8 (
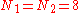) two-dimensional DCT.Each step from left to right and top to bottom is an increase in frequency by 1/2 cycle.
For example, moving right one from the top-left square yields a half-cycle increase in the horizontal frequency. Another move to the right yields two half-cycles. A move down yields two half-cycles horizontally and a half-cycle vertically. The source data (8x8) is transformed to a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of these 64 frequency squares.
Computation
Although the direct application of these formulas would require O(N2) operations, it is possible to compute the same thing with only O(N log N) complexity by factorizing the computation similarly to the fast Fourier transformFast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
(FFT). One can also compute DCTs via FFTs combined with O(N) pre- and post-processing steps. In general, O(N log N) methods to compute DCTs are known as fast cosine transform (FCT) algorithms.
The most efficient algorithms, in principle, are usually those that are specialized directly for the DCT, as opposed to using an ordinary FFT plus O(N) extra operations (see below for an exception). However, even "specialized" DCT algorithms (including all of those that achieve the lowest known arithmetic counts, at least for power-of-two
Power of two
In mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
sizes) are typically closely related to FFT algorithms—since DCTs are essentially DFTs of real-even data, one can design a fast DCT algorithm by taking an FFT and eliminating the redundant operations due to this symmetry. This can even be done automatically (Frigo & Johnson, 2005). Algorithms based on the Cooley–Tukey FFT algorithm are most common, but any other FFT algorithm is also applicable. For example, the Winograd FFT algorithm leads to minimal-multiplication algorithms for the DFT, albeit generally at the cost of more additions, and a similar algorithm was proposed by Feig & Winograd (1992) for the DCT. Because the algorithms for DFTs, DCTs, and similar transforms are all so closely related, any improvement in algorithms for one transform will theoretically lead to immediate gains for the other transforms as well (Duhamel & Vetterli, 1990).
While DCT algorithms that employ an unmodified FFT often have some theoretical overhead compared to the best specialized DCT algorithms, the former also have a distinct advantage: highly optimized FFT programs are widely available. Thus, in practice, it is often easier to obtain high performance for general lengths N with FFT-based algorithms. (Performance on modern hardware is typically not dominated simply by arithmetic counts, and optimization requires substantial engineering effort.) Specialized DCT algorithms, on the other hand, see widespread use for transforms of small, fixed sizes such as the
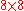DCT-II used in JPEGJPEG
In computing, JPEG . The degree of compression can be adjusted, allowing a selectable tradeoff between storage size and image quality. JPEG typically achieves 10:1 compression with little perceptible loss in image quality....
compression, or the small DCTs (or MDCTs) typically used in audio compression. (Reduced code size may also be a reason to use a specialized DCT for embedded-device applications.)
In fact, even the DCT algorithms using an ordinary FFT are sometimes equivalent to pruning the redundant operations from a larger FFT of real-symmetric data, and they can even be optimal from the perspective of arithmetic counts. For example, a type-II DCT is equivalent to a DFT of size
with real-even symmetry whose even-indexed elements are zero. One of the most common methods for computing this via an FFT (e.g. the method used in FFTPACKFFTPACK
FFTPACK is a package of Fortran subroutines for the fast Fourier transform. It includes complex, real, sine, cosine, and quarter-wave transforms. It was developed by Paul Swarztrauber of the National Center for Atmospheric Research....
and FFTW
FFTW
FFTW, for "Fastest Fourier Transform in the West", is a software library for computing discrete Fourier transforms , developed by Matteo Frigo and Steven G. Johnson at the Massachusetts Institute of Technology....
) was described by Narasimha & Peterson (1978) and Makhoul (1980), and this method in hindsight can be seen as one step of a radix-4 decimation-in-time Cooley–Tukey algorithm applied to the "logical" real-even DFT corresponding to the DCT II. (The radix-4 step reduces the size
DFT to four size- DFTs of real data, two of which are zero and two of which are equal to one another by the even symmetry, hence giving a single size- FFT of real data plus butterflies.) Because the even-indexed elements are zero, this radix-4 step is exactly the same as a split-radix step; if the subsequent size- real-data FFT is also performed by a real-data split-radix algorithmSplit-radix FFT algorithm
The split-radix FFT is a fast Fourier transform algorithm for computing the discrete Fourier transform , and was first described in an initially little-appreciated paper by R. Yavne and subsequently rediscovered simultaneously by various authors in 1984. The split-radix FFT is a fast Fourier...
(as in Sorensen et al., 1987), then the resulting algorithm actually matches what was long the lowest published arithmetic count for the power-of-two DCT-II (
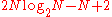real-arithmetic operations). So, there is nothing intrinsically bad about computing the DCT via an FFT from an arithmetic perspective—it is sometimes merely a question of whether the corresponding FFT algorithm is optimal. (As a practical matter, the function-call overhead in invoking a separate FFT routine might be significant for small , but this is an implementation rather than an algorithmic question since it can be solved by unrolling/inlining.)Example of IDCT
Consider this 8x8 grayscale image of capital letter A.DCT of the image.
-
Each basis function is multiplied by its coefficient and then this product is added to the final image.
See also
- JPEG - Contains an easier to understand example of DCT transformation
- Modified discrete cosine transformModified discrete cosine transformThe modified discrete cosine transform is a Fourier-related transform based on the type-IV discrete cosine transform , with the additional property of being lapped: it is designed to be performed on consecutive blocks of a larger dataset,...
- Discrete sine transformDiscrete sine transformIn mathematics, the discrete sine transform is a Fourier-related transform similar to the discrete Fourier transform , but using a purely real matrix...
- Discrete Fourier transformDiscrete Fourier transformIn mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
- List of Fourier-related transforms
External links
- The Discrete Cosine Transform (DCT): Theory and Application
- Implementation of MPEG integer approximation of 8x8 IDCT (ISO/IEC 23002-2)
- Matteo Frigo and Steven G. Johnson: FFTW, http://www.fftw.org/. A free (GPLGNU General Public LicenseThe GNU General Public License is the most widely used free software license, originally written by Richard Stallman for the GNU Project....
) C library that can compute fast DCTs (types I-IV) in one or more dimensions, of arbitrary size.