Minkowski inequality
Encyclopedia
In mathematical analysis
, the Minkowski inequality establishes that the Lp spaces
are normed vector space
s. Let S be a measure space, let 1 ≤ p ≤ ∞ and let f and g be elements of Lp(S). Then f + g is in Lp(S), and we have the triangle inequality
with equality for 1 < p < ∞ if and only if f and g are positively linearly dependent (which means f =
g or g = 
f for some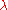 
≥ 0). Here, the norm is given by: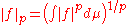
if p < ∞, or in the case p = ∞ by the essential supremum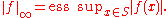
The Minkowski inequality is the triangle inequality in Lp(S). In fact, it is a special case of the more general fact
where it is easy to see that the right-hand side satisfies the triangular inequality.
Like Hölder's inequality
, the Minkowski inequality can be specialized to sequences and vectors by using the counting measure
:
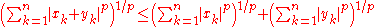
for all real
(or complex
) numbers x1, ..., xn, y1, ..., yn and where n is the cardinality of S (the number of elements in S).
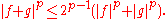
Indeed, here we use the fact that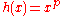
is convex
over
(for 
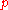greater than one) and so, if a and b are both positive then, by Jensen's inequality,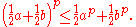
This means that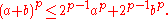
Now, we can legitimately talk about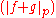
. If it is zero, then Minkowski's inequality holds. We now assume that 
is not zero. Using Hölder's inequality
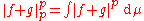
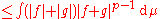
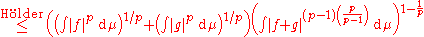
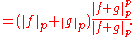
We obtain Minkowski's inequality by multiplying both sides by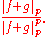
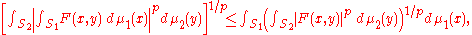
with obvious modifications in the case p = ∞. If p > 1, and both sides are finite, then equality holds only if |F(x,y)| = φ(x)ψ(y) a.e. for some non-negative measurable functions φ and ψ.
If μ1 is the counting measure on a two-point set S1 = {1,2}, then Minkowski's integral inequality gives the usual Minkowski inequality as a special case: for putting ƒi(y) = F(i,y) for i = 1,2, the integral inequality gives
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, the Minkowski inequality establishes that the Lp spaces
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
are normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
s. Let S be a measure space, let 1 ≤ p ≤ ∞ and let f and g be elements of Lp(S). Then f + g is in Lp(S), and we have the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
with equality for 1 < p < ∞ if and only if f and g are positively linearly dependent (which means f =
g or g = f for some 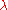≥ 0). Here, the norm is given by: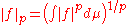if p < ∞, or in the case p = ∞ by the essential supremum
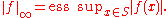
The Minkowski inequality is the triangle inequality in Lp(S). In fact, it is a special case of the more general fact
where it is easy to see that the right-hand side satisfies the triangular inequality.
Like Hölder's inequality
Hölder's inequality
In mathematical analysis Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of Lp spaces....
, the Minkowski inequality can be specialized to sequences and vectors by using the counting measure
Counting measure
In mathematics, the counting measure is an intuitive way to put a measure on any set: the "size" of a subset is taken to be the number of elements in the subset, if the subset is finite, and ∞ if the subset is infinite....
:
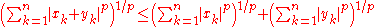
for all real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
(or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
) numbers x1, ..., xn, y1, ..., yn and where n is the cardinality of S (the number of elements in S).
Proof
First, we prove that f+g has finite p-norm if f and g both do, which follows by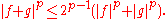Indeed, here we use the fact that
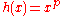is convexConvex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
over
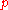(for greater than one) and so, if a and b are both positive then, by Jensen's inequality,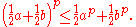This means that
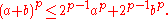
Now, we can legitimately talk about
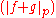. If it is zero, then Minkowski's inequality holds. We now assume that is not zero. Using Hölder's inequalityHölder's inequality
In mathematical analysis Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of Lp spaces....
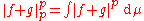
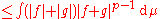
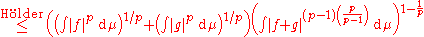
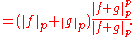
We obtain Minkowski's inequality by multiplying both sides by
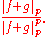
Minkowski's integral inequality
Suppose that (S1,μ1) and (S2,μ2) are two measure spaces and F : S1×S2 → R is measurable. Then Minkowski's integral inequality is , :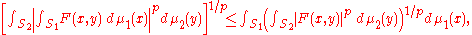with obvious modifications in the case p = ∞. If p > 1, and both sides are finite, then equality holds only if |F(x,y)| = φ(x)ψ(y) a.e. for some non-negative measurable functions φ and ψ.
If μ1 is the counting measure on a two-point set S1 = {1,2}, then Minkowski's integral inequality gives the usual Minkowski inequality as a special case: for putting ƒi(y) = F(i,y) for i = 1,2, the integral inequality gives