
Addition
Encyclopedia

Addition is a mathematical operation
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
that represents combining collections of objects together into a larger collection. It is signified by the plus sign (+). For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples. Therefore, 3 + 2 = 5. Besides counting fruits, addition can also represent combining other physical and abstract quantities using different kinds of numbers: negative numbers, fractions
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
, irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s, vectors, decimals and more.
Addition follows several important patterns. It is commutative
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
, meaning that order does not matter, and it is associative
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
, meaning that when one adds more than two numbers, order in which addition is performed does not matter (see Summation
Summation
Summation is the operation of adding a sequence of numbers; the result is their sum or total. If numbers are added sequentially from left to right, any intermediate result is a partial sum, prefix sum, or running total of the summation. The numbers to be summed may be integers, rational numbers,...
). Repeated addition of 1 is the same as counting
Counting
Counting is the action of finding the number of elements of a finite set of objects. The traditional way of counting consists of continually increasing a counter by a unit for every element of the set, in some order, while marking those elements to avoid visiting the same element more than once,...
; addition of 0
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
and multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
. All of these rules can be proven
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
, starting with the addition of natural numbers and generalizing up through the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s and beyond. General binary operations that continue these patterns are studied in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
.
Performing addition is one of the simplest numerical tasks. Addition of very small numbers is accessible to toddlers; the most basic task, 1 + 1, can be performed by infants as young as five months and even some animals. In primary education
Primary education
A primary school is an institution in which children receive the first stage of compulsory education known as primary or elementary education. Primary school is the preferred term in the United Kingdom and many Commonwealth Nations, and in most publications of the United Nations Educational,...
, children learn to add numbers in the decimal
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
system, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancient abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
to the modern computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
, where research on the most efficient implementations of addition continues to this day.
Notation and terminology
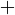
Plus and minus signs
The plus and minus signs are mathematical symbols used to represent the notions of positive and negative as well as the operations of addition and subtraction. Their use has been extended to many other meanings, more or less analogous...
"+" between the terms; that is, in infix notation
Infix notation
Infix notation is the common arithmetic and logical formula notation, in which operators are written infix-style between the operands they act on . It is not as simple to parse by computers as prefix notation or postfix notation Infix notation is the common arithmetic and logical formula notation,...
. The result is expressed with an equals sign
Equals sign
The equality sign, equals sign, or "=" is a mathematical symbol used to indicate equality. It was invented in 1557 by Robert Recorde. The equals sign is placed between the things stated to have the same value, as in an equation...
. For example,
 (verbally, "one plus one equals two")
(verbally, "one plus one equals two")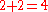 (verbally, "two plus two equals four")
(verbally, "two plus two equals four") (see "associativity" below)
(see "associativity" below) (see "multiplication" below)
(see "multiplication" below)There are also situations where addition is "understood" even though no symbol appears:
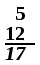
- A column of numbers, with the last number in the column underlineUnderlineAn underline, also called an underscore, is one or more horizontal lines immediately below a portion of writing. Single, and occasionally double , underlining was originally used in hand-written or typewritten documents to emphasise text...
d, usually indicates that the numbers in the column are to be added, with the sum written below the underlined number. - A whole number followed immediately by a fractionFraction (mathematics)A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
indicates the sum of the two, called a mixed number. For example,
3½ = 3 + ½ = 3.5.
This notation can cause confusion since in most other contexts juxtaposition denotes multiplicationMultiplicationMultiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
instead.
The sum of a series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
of related numbers can be expressed through capital sigma notation, which compactly denotes iteration. For example,
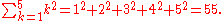
The numbers or the objects to be added in general addition are called the "terms", the "addends", or the "summands";
this terminology carries over to the summation of multiple terms.
This is to be distinguished from factors, which are multiplied
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
.
Some authors call the first addend the augend. In fact, during the Renaissance
Renaissance
The Renaissance was a cultural movement that spanned roughly the 14th to the 17th century, beginning in Italy in the Late Middle Ages and later spreading to the rest of Europe. The term is also used more loosely to refer to the historical era, but since the changes of the Renaissance were not...
, many authors did not consider the first addend an "addend" at all. Today, due to the symmetry of addition, "augend" is rarely used, and both terms are generally called addends.
All of this terminology derives from Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
. "Addition" and "add" are English
English language
English is a West Germanic language that arose in the Anglo-Saxon kingdoms of England and spread into what was to become south-east Scotland under the influence of the Anglian medieval kingdom of Northumbria...
words derived from the Latin verb
Verb
A verb, from the Latin verbum meaning word, is a word that in syntax conveys an action , or a state of being . In the usual description of English, the basic form, with or without the particle to, is the infinitive...
addere, which is in turn a compound
Compound (linguistics)
In linguistics, a compound is a lexeme that consists of more than one stem. Compounding or composition is the word formation that creates compound lexemes...
of ad "to" and dare "to give", from the Proto-Indo-European root
Proto-Indo-European root
The roots of the reconstructed Proto-Indo-European language are basic parts of words that carry a lexical meaning, so-called morphemes. PIE roots always have verbal meaning like "to eat" or "to run", as opposed to nouns , adjectives , or other parts of speech. Roots never occur alone in the language...
"to give"; thus to add is to give to. Using the gerundive
Gerundive
In linguistics, a gerundive is a particular verb form. The term is applied very differently to different languages; depending on the language, gerundives may be verbal adjectives, verbal adverbs, or finite verbs...
suffix
Affix
An affix is a morpheme that is attached to a word stem to form a new word. Affixes may be derivational, like English -ness and pre-, or inflectional, like English plural -s and past tense -ed. They are bound morphemes by definition; prefixes and suffixes may be separable affixes...
-nd results in "addend", "thing to be added". Likewise from augere "to increase", one gets "augend", "thing to be increased".

Noun
In linguistics, a noun is a member of a large, open lexical category whose members can occur as the main word in the subject of a clause, the object of a verb, or the object of a preposition .Lexical categories are defined in terms of how their members combine with other kinds of...
summa "the highest, the top" and associated verb summare. This is appropriate not only because the sum of two positive numbers is greater than either, but because it was once common to add upward, contrary to the modern practice of adding downward, so that a sum was literally higher than the addends.
Addere and summare date back at least to Boethius
Anicius Manlius Severinus Boethius
Anicius Manlius Severinus Boëthius, commonly called Boethius was a philosopher of the early 6th century. He was born in Rome to an ancient and important family which included emperors Petronius Maximus and Olybrius and many consuls. His father, Flavius Manlius Boethius, was consul in 487 after...
, if not to earlier Roman writers such as Vitruvius
Vitruvius
Marcus Vitruvius Pollio was a Roman writer, architect and engineer, active in the 1st century BC. He is best known as the author of the multi-volume work De Architectura ....
and Frontinus
Sextus Julius Frontinus
Sextus Julius Frontinus was one of the most distinguished Roman aristocrats of the late 1st century AD, but is best known to the post-Classical world as an author of technical treatises, especially one dealing with the aqueducts of Rome....
; Boethius also used several other terms for the addition operation. The later Middle English
Middle English
Middle English is the stage in the history of the English language during the High and Late Middle Ages, or roughly during the four centuries between the late 11th and the late 15th century....
terms "adden" and "adding" were popularized by Chaucer
Geoffrey Chaucer
Geoffrey Chaucer , known as the Father of English literature, is widely considered the greatest English poet of the Middle Ages and was the first poet to have been buried in Poet's Corner of Westminster Abbey...
.
Interpretations
Addition is used to model countless physical processes. Even for the simple case of adding natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s, there are many possible interpretations and even more visual representations.
Combining sets
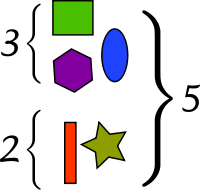
- When two or more disjoint collections are combined into a single collection, the number of objects in the single collection is the sum of the number of objects in the original collections.
This interpretation is easy to visualize, with little danger of ambiguity. It is also useful in higher mathematics; for the rigorous definition it inspires, see Natural numbers below. However, it is not obvious how one should extend this version of addition to include fractional numbers or negative numbers.
One possible fix is to consider collections of objects that can be easily divided, such as pie
Pie
A pie is a baked dish which is usually made of a pastry dough casing that covers or completely contains a filling of various sweet or savoury ingredients....
s or, still better, segmented rods. Rather than just combining collections of segments, rods can be joined end-to-end, which illustrates another conception of addition: adding not the rods but the lengths of the rods.
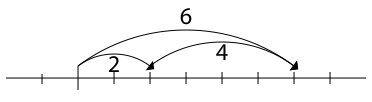
Extending a length
A second interpretation of addition comes from extending an initial length by a given length:- When an original length is extended by a given amount, the final length is the sum of the original length and the length of the extension.

Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
that combines a and b, in an algebraic sense, or it can be interpreted as the addition of b more units to a. Under the latter interpretation, the parts of a sum a + b play asymmetric roles, and the operation a + b is viewed as applying the unary operation
Unary operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
+b to a. Instead of calling both a and b addends, it is more appropriate to call a the augend in this case, since a plays a passive role. The unary view is also useful when discussing subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
, because each unary addition operation has an inverse unary subtraction operation, and vice versa.
Commutativity

- a + b = b + a.
The fact that addition is commutative is known as the "commutative law of addition". This phrase suggests that there are other commutative laws: for example, there is a commutative law of multiplication. However, many binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s are not commutative, such as subtraction and division, so it is misleading to speak of an unqualified "commutative law".
Associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
, which comes up when one tries to define repeated addition. Should the expression
- "a + b + c"
be defined to mean (a + b) + c or a + (b + c)? That addition is associative tells us that the choice of definition is irrelevant. For any three numbers a, b, and c, it is true that
- (a + b) + c = a + (b + c).
For example, (1 + 2) + 3 = 3 + 3 = 6 = 1 + 5 = 1 + (2 + 3).
Not all operations are associative, so in expressions with other operations like subtraction, it is important to specify the order of operations
Order of operations
In mathematics and computer programming, the order of operations is a rule used to clarify unambiguously which procedures should be performed first in a given mathematical expression....
.
Zero and one
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
to any number, the quantity does not change; zero is the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
for addition, also known as the additive identity
Additive identity
In mathematics the additive identity of a set which is equipped with the operation of addition is an element which, when added to any element x in the set, yields x...
. In symbols, for any a,
- a + 0 = 0 + a = a.
This law was first identified in Brahmagupta
Brahmagupta
Brahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
's Brahmasphutasiddhanta
Brahmasphutasiddhanta
The main work of Brahmagupta, Brāhmasphuṭasiddhānta , written c.628, contains ideas including a good understanding of the mathematical role of zero, rules for manipulating both negative and positive numbers, a method for computing square roots, methods of solving linear and some quadratic...
in 628, although he wrote it as three separate laws, depending on whether a is negative, positive, or zero itself, and he used words rather than algebraic symbols. Later Indian mathematicians refined the concept; around the year 830, Mahavira
Mahavira (mathematician)
Mahavira was a 9th-century Indian Jain mathematician from Gulbarga who asserted that the square root of a negative number did not exist. He gave the sum of a series whose terms are squares of an arithmetical progression and empirical rules for area and perimeter of an ellipse. He was patronised by...
wrote, "zero becomes the same as what is added to it", corresponding to the unary statement 0 + a = a. In the 12th century, Bhaskara wrote, "In the addition of cipher, or subtraction of it, the quantity, positive or negative, remains the same", corresponding to the unary statement a + 0 = a.
In the context of integers, addition of one also plays a special role: for any integer a, the integer (a + 1) is the least integer greater than a, also known as the successor of a. Because of this succession, the value of some a + b can also be seen as the
 successor of a, making addition iterated succession.
successor of a, making addition iterated succession.Units
To numerically add physical quantities with unitsUnits of measurement
A unit of measurement is a definite magnitude of a physical quantity, defined and adopted by convention and/or by law, that is used as a standard for measurement of the same physical quantity. Any other value of the physical quantity can be expressed as a simple multiple of the unit of...
, they must first be expressed with common units. For example, if a measure of 5 feet is extended by 2 inches, the sum is 62 inches, since 60 inches is synonymous with 5 feet. On the other hand, it is usually meaningless to try to add 3 meters and 4 square meters, since those units are incomparable; this sort of consideration is fundamental in dimensional analysis
Dimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
.
Innate ability
Studies on mathematical development starting around the 1980s have exploited the phenomenon of habituationHabituation
Habituation can be defined as a process or as a procedure. As a process it is defined as a decrease in an elicited behavior resulting from the repeated presentation of an eliciting stimulus...
: infant
Infant
A newborn or baby is the very young offspring of a human or other mammal. A newborn is an infant who is within hours, days, or up to a few weeks from birth. In medical contexts, newborn or neonate refers to an infant in the first 28 days after birth...
s look longer at situations that are unexpected. A seminal experiment by Karen Wynn in 1992 involving Mickey Mouse
Mickey Mouse
Mickey Mouse is a cartoon character created in 1928 by Walt Disney and Ub Iwerks at The Walt Disney Studio. Mickey is an anthropomorphic black mouse and typically wears red shorts, large yellow shoes, and white gloves...
dolls manipulated behind a screen demonstrated that five-month-old infants expect 1 + 1 to be 2, and they are comparatively surprised when a physical situation seems to imply that 1 + 1 is either 1 or 3. This finding has since been affirmed by a variety of laboratories using different methodologies. Another 1992 experiment with older toddler
Toddler
A toddler is a young child, usually defined as being between the ages of one and three. Registered nurse, midwife and author, Robin Barker, states 'Any time from eight months onwards your baby will begin to realise he is a separate person from you...
s, between 18 to 35 months, exploited their development of motor control by allowing them to retrieve ping-pong balls from a box; the youngest responded well for small numbers, while older subjects were able to compute sums up to 5.
Even some nonhuman animals show a limited ability to add, particularly primate
Primate
A primate is a mammal of the order Primates , which contains prosimians and simians. Primates arose from ancestors that lived in the trees of tropical forests; many primate characteristics represent adaptations to life in this challenging three-dimensional environment...
s. In a 1995 experiment imitating Wynn's 1992 result (but using eggplants instead of dolls), rhesus macaque
Rhesus Macaque
The Rhesus macaque , also called the Rhesus monkey, is one of the best-known species of Old World monkeys. It is listed as Least Concern in the IUCN Red List of Threatened Species in view of its wide distribution, presumed large population, and its tolerance of a broad range of habitats...
s and cottontop tamarin
Cottontop Tamarin
The cotton-top tamarin , also known as the Pinché tamarin, is a small New World monkey weighing less than 1 lb...
s performed similarly to human infants. More dramatically, after being taught the meanings of the Arabic numerals
Arabic numerals
Arabic numerals or Hindu numerals or Hindu-Arabic numerals or Indo-Arabic numerals are the ten digits . They are descended from the Hindu-Arabic numeral system developed by Indian mathematicians, in which a sequence of digits such as "975" is read as a numeral...
0 through 4, one chimpanzee
Common Chimpanzee
The common chimpanzee , also known as the robust chimpanzee, is a great ape. Colloquially, the common chimpanzee is often called the chimpanzee , though technically this term refers to both species in the genus Pan: the common chimpanzee and the closely related bonobo, formerly called the pygmy...
was able to compute the sum of two numerals without further training.
Elementary methods
Typically children master the art of countingCounting
Counting is the action of finding the number of elements of a finite set of objects. The traditional way of counting consists of continually increasing a counter by a unit for every element of the set, in some order, while marking those elements to avoid visiting the same element more than once,...
first. When asked a problem requiring two items and three items to be combined, young children will model the situation with physical objects, often fingers or a drawing, and then count the total. As they gain experience, they will learn or discover the strategy of "counting-on": asked to find two plus three, children count three past two, saying "three, four, five" (usually ticking off fingers), and arriving at five. This strategy seems almost universal; children can easily pick it up from peers or teachers. Most discover it independently. With additional experience, children learn to add more quickly by exploiting the commutativity of addition by counting up from the larger number, in this case starting with three and counting "four, five." Eventually children begin to recall certain addition facts ("number bond
Number bond
In mathematics education at primary school level, a number bond is a simple addition sum which has become so familiar that a child can recognise it and complete it almost instantly, with recall as automatic as that of an entry from a multiplication table in multiplication.For example,5 + 2 = 7\;A...
s"), either through experience or rote memorization. Once some facts are committed to memory, children begin to derive unknown facts from known ones. For example, a child who is asked to add six and seven may know that 6+6=12 and then reason that 6+7 will be one more, or 13. Such derived facts can be found very quickly and most elementary school children eventually rely on a mixture of memorized and derived facts to add fluently.
Decimal system
The prerequisite to addition in the decimalDecimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
system is the fluent recall or derivation of the 100 single-digit "addition facts". One could memorize all the facts by rote
Rote learning
Rote learning is a learning technique which focuses on memorization. The major practice involved in rote learning is learning by repetition by which students commit information to memory in a highly structured way. The idea is that one will be able to quickly recall the meaning of the material the...
, but pattern-based strategies are more enlightening and, for most people, more efficient:
- One or two more: Adding 1 or 2 is a basic task, and it can be accomplished through counting on or, ultimately, intuitionIntuition (knowledge)Intuition is the ability to acquire knowledge without inference or the use of reason. "The word 'intuition' comes from the Latin word 'intueri', which is often roughly translated as meaning 'to look inside'’ or 'to contemplate'." Intuition provides us with beliefs that we cannot necessarily justify...
. - Zero: Since zero is the additive identity, adding zero is trivial. Nonetheless, some children are introduced to addition as a process that always increases the addends; word problemsWord problem (mathematics education)In mathematics education, the term word problem is often used to refer to any math exercise where significant background information on the problem is presented as text rather than in mathematical notation...
may help rationalize the "exception" of zero. - Doubles: Adding a number to itself is related to counting by two and to multiplicationMultiplicationMultiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
. Doubles facts form a backbone for many related facts, and fortunately, children find them relatively easy to grasp. - Near-doubles: Sums such as 6+7=13 can be quickly derived from the doubles fact 6+6=12 by adding one more, or from 7+7=14 but subtracting one.
- Five and ten: Sums of the form 5+x and 10+x are usually memorized early and can be used for deriving other facts. For example, 6+7=13 can be derived from 5+7=12 by adding one more.
- Making ten: An advanced strategy uses 10 as an intermediate for sums involving 8 or 9; for example, 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14.
As children grow older, they will commit more facts to memory, and learn to derive other facts rapidly and fluently. Many children never commit all the facts to memory, but can still find any basic fact quickly.
The standard algorithm for adding multidigit numbers is to align the addends vertically and add the columns, starting from the ones column on the right. If a column exceeds ten, the extra digit is "carried" into the next column. An alternate strategy starts adding from the most significant digit on the left; this route makes carrying a little clumsier, but it is faster at getting a rough estimate of the sum. There are many other alternative methods
Reform mathematics
Reform mathematics is an approach to mathematics education, particularly in North America. It is based on principles explained in 1989 by the National Council of Teachers of Mathematics . The NCTM document, Curriculum and Evaluation Standards for School Mathematics, attempted to set forth a vision...
.
- Fraction: Addition
- Scientific notation: Operations
Computers
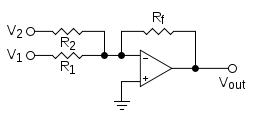
Analog computer
An analog computer is a form of computer that uses the continuously-changeable aspects of physical phenomena such as electrical, mechanical, or hydraulic quantities to model the problem being solved...
s work directly with physical quantities, so their addition mechanisms depend on the form of the addends. A mechanical adder might represent two addends as the positions of sliding blocks, in which case they can be added with an averaging
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
lever
Lever
In physics, a lever is a rigid object that is used with an appropriate fulcrum or pivot point to either multiply the mechanical force that can be applied to another object or resistance force , or multiply the distance and speed at which the opposite end of the rigid object travels.This leverage...
. If the addends are the rotation speeds of two shafts
Axle
An axle is a central shaft for a rotating wheel or gear. On wheeled vehicles, the axle may be fixed to the wheels, rotating with them, or fixed to its surroundings, with the wheels rotating around the axle. In the former case, bearings or bushings are provided at the mounting points where the axle...
, they can be added with a differential
Differential (mechanics)
A differential is a device, usually, but not necessarily, employing gears, capable of transmitting torque and rotation through three shafts, almost always used in one of two ways: in one way, it receives one input and provides two outputs—this is found in most automobiles—and in the other way, it...
. A hydraulic adder can add the pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
s in two chambers by exploiting Newton's second law
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
to balance forces on an assembly of piston
Piston
A piston is a component of reciprocating engines, reciprocating pumps, gas compressors and pneumatic cylinders, among other similar mechanisms. It is the moving component that is contained by a cylinder and is made gas-tight by piston rings. In an engine, its purpose is to transfer force from...
s. The most common situation for a general-purpose analog computer is to add two voltage
Voltage
Voltage, otherwise known as electrical potential difference or electric tension is the difference in electric potential between two points — or the difference in electric potential energy per unit charge between two points...
s (referenced to ground
Ground (electricity)
In electrical engineering, ground or earth may be the reference point in an electrical circuit from which other voltages are measured, or a common return path for electric current, or a direct physical connection to the Earth....
); this can be accomplished roughly with a resistor
Resistor
A linear resistor is a linear, passive two-terminal electrical component that implements electrical resistance as a circuit element.The current through a resistor is in direct proportion to the voltage across the resistor's terminals. Thus, the ratio of the voltage applied across a resistor's...
network
Electronic circuit
An electronic circuit is composed of individual electronic components, such as resistors, transistors, capacitors, inductors and diodes, connected by conductive wires or traces through which electric current can flow...
, but a better design exploits an operational amplifier
Operational amplifier
An operational amplifier is a DC-coupled high-gain electronic voltage amplifier with a differential input and, usually, a single-ended output...
.
Addition is also fundamental to the operation of digital computers
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
, where the efficiency of addition, in particular the carry mechanism, is an important limitation to overall performance.

Adding machine
An adding machine was a class of mechanical calculator, usually specialized for bookkeeping calculations.In the United States, the earliest adding machines were usually built to read in dollars and cents. Adding machines were ubiquitous office equipment until they were phased out in favor of...
s, mechanical calculators whose primary function was addition, were the earliest automatic, digital computers. Wilhelm Schickard
Wilhelm Schickard
Wilhelm Schickard was a German polymath who designed a calculating machine in 1623, twenty years before the Pascaline of Blaise Pascal. Unfortunately a fire destroyed the machine as it was being built in 1624 and Schickard decided to abandon his project...
's 1623 Calculating Clock could add and subtract, but it was severely limited by an awkward carry mechanism. Burnt during its construction in 1624 and unknown to the world for more than three centuries, it was rediscovered in 1957 and therefore had no impact on the development of mechanical calculators. Blaise Pascal
Blaise Pascal
Blaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...
invented the mechanical calculator in 1642 with an ingenious gravity-assisted carry mechanism. Pascal's calculator
Pascal's calculator
Blaise Pascal invented the mechanical calculator in 1642. He conceived it while trying to help his father who had been assigned the task of reorganizing the tax revenues of the French province of Haute-Normandie ; first called Arithmetic Machine, Pascal's Calculator and later Pascaline, it could...
was limited by its carry mechanism in a different sense: its wheels turned only one way, so it could add but not subtract, except by the method of complements
Method of complements
In mathematics and computing, the method of complements is a technique used to subtract one number from another using only addition of positive numbers. This method was commonly used in mechanical calculators and is still used in modern computers...
. By 1674 Gottfried Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
made the first mechanical multiplier; it was still powered, if not motivated, by addition.

Adder (electronics)
In electronics, an adder or summer is a digital circuit that performs addition of numbers.In many computers and other kinds of processors, adders are used not only in the arithmetic logic unit, but also in other parts of the processor, where they are used to calculate addresses, table indices, and...
execute integer addition in electronic digital computers, usually using binary arithmetic. The simplest architecture is the ripple carry adder, which follows the standard multi-digit algorithm taught to children. One slight improvement is the carry skip
Carry bypass adder
A carry-bypass adder is an adder implementatin that improves on the delay of a ripple-carry adder.The two addends are split in blocks of n bits. The output carry of each block is dependent on the input carry only if, for each of the n bits in the block, at least one addend has a 1 bit...
design, again following human intuition; one does not perform all the carries in computing 999 + 1, but one bypasses the group of 9s and skips to the answer.
Since they compute digits one at a time, the above methods are too slow for most modern purposes.
In modern digital computers, integer addition is typically the fastest arithmetic instruction, yet it has the largest impact on performance, since it underlies all the floating-point
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
operations as well as such basic tasks as address
Memory address
A digital computer's memory, more specifically main memory, consists of many memory locations, each having a memory address, a number, analogous to a street address, at which computer programs store and retrieve, machine code or data. Most application programs do not directly read and write to...
generation during memory access and fetching instructions during branching
Control flow
In computer science, control flow refers to the order in which the individual statements, instructions, or function calls of an imperative or a declarative program are executed or evaluated....
. To increase speed, modern designs calculate digits in parallel
Parallel algorithm
In computer science, a parallel algorithm or concurrent algorithm, as opposed to a traditional sequential algorithm, is an algorithm which can be executed a piece at a time on many different processing devices, and then put back together again at the end to get the correct result.Some algorithms...
; these schemes go by such names as carry select, carry lookahead, and the Ling
Ling adder
In electronics, an adder is a combinatorial or sequential logic element which computes the n-bit sum of two numbers. The family of Ling adders is a particularly fast adder and is designed using H. Ling's equations and generally implemented in BiCMOS. Samuel Naffziger of Hewlett Packard presented...
pseudocarry. Almost all modern implementations are, in fact, hybrids of these last three designs.
Unlike addition on paper
Paper
Paper is a thin material mainly used for writing upon, printing upon, drawing or for packaging. It is produced by pressing together moist fibers, typically cellulose pulp derived from wood, rags or grasses, and drying them into flexible sheets....
, addition on a computer often changes the addends. On the ancient abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
and adding board, both addends are destroyed, leaving only the sum. The influence of the abacus on mathematical thinking was strong enough that early Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
texts often claimed that in the process of adding "a number to a number", both numbers vanish. In modern times, the ADD instruction of a microprocessor
Microprocessor
A microprocessor incorporates the functions of a computer's central processing unit on a single integrated circuit, or at most a few integrated circuits. It is a multipurpose, programmable device that accepts digital data as input, processes it according to instructions stored in its memory, and...
replaces the augend with the sum but preserves the addend. In a high-level programming language
High-level programming language
A high-level programming language is a programming language with strong abstraction from the details of the computer. In comparison to low-level programming languages, it may use natural language elements, be easier to use, or be from the specification of the program, making the process of...
, evaluating a + b does not change either a or b; to change the value of a one uses the addition assignment operator a += b.
Addition of natural and real numbers
To prove the usual properties of addition, one must first define addition for the context in question. Addition is first defined on the natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s. In set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, addition is then extended to progressively larger sets that include the natural numbers: the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, and the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. (In mathematics education
Mathematics education
In contemporary education, mathematics education is the practice of teaching and learning mathematics, along with the associated scholarly research....
, positive fractions are added before negative numbers are even considered; this is also the historical route.)
Natural numbers
There are two popular ways to define the sum of two natural numbers a and b. If one defines natural numbers to be the cardinalitiesCardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
of finite sets, (the cardinality of a set is the number of elements in the set), then it is appropriate to define their sum as follows:
- Let N(S) be the cardinality of a set S. Take two disjoint sets A and B, with N(A) = a and N(B) = b. Then a + b is defined as
 .
.
Here, A U B is the union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of A and B. An alternate version of this definition allows A and B to possibly overlap and then takes their disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
, a mechanism that allows common elements to be separated out and therefore counted twice.
The other popular definition is recursive:
- Let n+ be the successor of n, that is the number following n in the natural numbers, so 0+=1, 1+=2. Define a + 0 = a. Define the general sum recursively by a + (b+) = (a + b)+. Hence 1+1=1+0+=(1+0)+=1+=2.
Again, there are minor variations upon this definition in the literature. Taken literally, the above definition is an application of the Recursion Theorem
Recursion theorem
Recursion theorem can refer to:* The recursion theorem in set theory* Kleene's recursion theorem, also called the fixed point theorem, in computability theory...
on the poset N2. On the other hand, some sources prefer to use a restricted Recursion Theorem that applies only to the set of natural numbers. One then considers a to be temporarily "fixed", applies recursion on b to define a function "a + ", and pastes these unary operations for all a together to form the full binary operation.
This recursive formulation of addition was developed by Dedekind as early as 1854, and he would expand upon it in the following decades. He proved the associative and commutative properties, among others, through mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
; for examples of such inductive proofs, see Addition of natural numbers.
Integers
The simplest conception of an integer is that it consists of an absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
(which is a natural number) and a sign
Sign (mathematics)
In mathematics, the word sign refers to the property of being positive or negative. Every nonzero real number is either positive or negative, and therefore has a sign. Zero itself is signless, although in some contexts it makes sense to consider a signed zero...
(generally either positive or negative). The integer zero is a special third case, being neither positive nor negative. The corresponding definition of addition must proceed by cases:
- For an integer n, let |n| be its absolute value. Let a and b be integers. If either a or b is zero, treat it as an identity. If a and b are both positive, define a + b = |a| + |b|. If a and b are both negative, define a + b = −(|a|+|b|). If a and b have different signs, define a + b to be the difference between |a| and |b|, with the sign of the term whose absolute value is larger.
Although this definition can be useful for concrete problems, it is far too complicated to produce elegant general proofs; there are too many cases to consider.
A much more convenient conception of the integers is the Grothendieck group
Grothendieck group
In mathematics, the Grothendieck group construction in abstract algebra constructs an abelian group from a commutative monoid in the best possible way...
construction. The essential observation is that every integer can be expressed (not uniquely) as the difference of two natural numbers, so we may as well define an integer as the difference of two natural numbers. Addition is then defined to be compatible with subtraction:
- Given two integers a − b and c − d, where a, b, c, and d are natural numbers, define (a − b) + (c − d) = (a + c) − (b + d).
Rational numbers (Fractions)
Addition of rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s can be computed using the least common denominator, but a conceptually simpler definition involves only integer addition and multiplication:
- Define
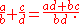
The commutativity and associativity of rational addition is an easy consequence of the laws of integer arithmetic. For a more rigorous and general discussion, see field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
.
Real numbers
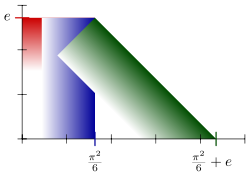
A common construction of the set of real numbers is the Dedekind completion of the set of rational numbers. A real number is defined to be a Dedekind cut
Dedekind cut
In mathematics, a Dedekind cut, named after Richard Dedekind, is a partition of the rationals into two non-empty parts A and B, such that all elements of A are less than all elements of B, and A contains no greatest element....
of rationals: a non-empty set of rationals that is closed downward and has no greatest element
Greatest element
In mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set is an element of S which is greater than or equal to any other element of S. The term least element is defined dually...
. The sum of real numbers a and b is defined element by element:
- Define
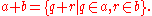
This definition was first published, in a slightly modified form, by Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
in 1872.
The commutativity and associativity of real addition are immediate; defining the real number 0 to be the set of negative rationals, it is easily seen to be the additive identity. Probably the trickiest part of this construction pertaining to addition is the definition of additive inverses.
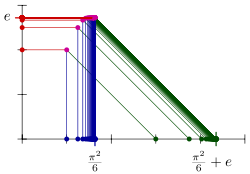
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
of rationals, lim an. Addition is defined term by term:
- Define
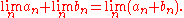
This definition was first published by Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
, also in 1872, although his formalism was slightly different.
One must prove that this operation is well-defined, dealing with co-Cauchy sequences. Once that task is done, all the properties of real addition follow immediately from the properties of rational numbers. Furthermore, the other arithmetic operations, including multiplication, have straightforward, analogous definitions.
Generalizations
- There are many things that can be added: numbers, vectors, matrices, spaces, shapes, sets, functions, equations, strings, chains... —Alexander Bogomolny
There are many binary operations that can be viewed as generalizations of the addition operation on the real numbers. The field of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
is centrally concerned with such generalized operations, and they also appear in set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
and category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
.
Addition in abstract algebra
In linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
is an algebraic structure that allows for adding any two vectors
Coordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
and for scaling vectors. A familiar vector space is the set of all ordered pairs of real numbers; the ordered pair (a,b) is interpreted as a vector from the origin in the Euclidean plane to the point (a,b) in the plane. The sum of two vectors is obtained by adding their individual coordinates: + (c,d) = (a+c,b+d).
This addition operation is central to classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, in which vectors are interpreted as force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
s.
In modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
, the set of integers modulo 12 has twelve elements; it inherits an addition operation from the integers that is central to musical set theory. The set of integers modulo 2 has just two elements; the addition operation it inherits is known in Boolean logic
Boolean logic
Boolean algebra is a logical calculus of truth values, developed by George Boole in the 1840s. It resembles the algebra of real numbers, but with the numeric operations of multiplication xy, addition x + y, and negation −x replaced by the respective logical operations of...
as the "exclusive or" function. In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the sum of two angle measures
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
is often taken to be their sum as real numbers modulo 2π. This amounts to an addition operation on the circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, which in turn generalizes to addition operations on many-dimensional tori
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
.
The general theory of abstract algebra allows an "addition" operation to be any associative and commutative operation on a set. Basic algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s with such an addition operation include commutative monoids and abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s.
Addition in set theory and category theory
A far-reaching generalization of addition of natural numbers is the addition of ordinal numberOrdinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
s and cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s in set theory. These give two different generalizations of addition of natural numbers to the transfinite.
Unlike most addition operations, addition of ordinal numbers is not commutative.
Addition of cardinal numbers, however, is a commutative operation closely related to the disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
operation.
In category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, disjoint union is seen as a particular case of the coproduct
Coproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
operation, and general coproducts are perhaps the most abstract of all the generalizations of addition. Some coproducts, such as Direct sum
Direct sum
In mathematics, one can often define a direct sum of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets , together with a suitably defined structure. More abstractly, the direct sum is often, but not always, the coproduct in the category in question...
and Wedge sum
Wedge sum
In topology, the wedge sum is a "one-point union" of a family of topological spaces. Specifically, if X and Y are pointed spaces the wedge sum of X and Y is the quotient of the disjoint union of X and Y by the identification x0 ∼ y0:X\vee Y = \;/ \sim,\,where ∼ is the...
, are named to evoke their connection with addition.
Arithmetic
SubtractionSubtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
can be thought of as a kind of addition—that is, the addition of an additive inverse
Additive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
. Subtraction is itself a sort of inverse to addition, in that adding x and subtracting x are inverse function
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
s.
Given a set with an addition operation, one cannot always define a corresponding subtraction operation on that set; the set of natural numbers is a simple example. On the other hand, a subtraction operation uniquely determines an addition operation, an additive inverse operation, and an additive identity; for this reason, an additive group can be described as a set that is closed under subtraction.
Multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
can be thought of as repeated addition. If a single term x appears in a sum n times, then the sum is the product of n and x. If n is not a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
, the product may still make sense; for example, multiplication by −1 yields the additive inverse
Additive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
of a number.

Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
:
- ea + b = ea eb.
This identity allows multiplication to be carried out by consulting a table
Mathematical table
Before calculators were cheap and plentiful, people would use mathematical tables —lists of numbers showing the results of calculation with varying arguments— to simplify and drastically speed up computation...
of logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
s and computing addition by hand; it also enables multiplication on a slide rule
Slide rule
The slide rule, also known colloquially as a slipstick, is a mechanical analog computer. The slide rule is used primarily for multiplication and division, and also for functions such as roots, logarithms and trigonometry, but is not normally used for addition or subtraction.Slide rules come in a...
. The formula is still a good first-order approximation in the broad context of Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s, where it relates multiplication of infinitesimal group elements with addition of vectors in the associated Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
.
There are even more generalizations of multiplication than addition. In general, multiplication operations always distribute
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
over addition; this requirement is formalized in the definition of a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
. In some contexts, such as the integers, distributivity over addition and the existence of a multiplicative identity is enough to uniquely determine the multiplication operation. The distributive property also provides information about addition; by expanding the product (1 + 1)(a + b) in both ways, one concludes that addition is forced to be commutative. For this reason, ring addition is commutative in general.
Division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
is an arithmetic operation remotely related to addition. Since a/b = a(b−1), division is right distributive over addition: (a + b) / c = a / c + b / c. However, division is not left distributive over addition; 1/ (2 + 2) is not the same as 1/2 + 1/2.
Ordering
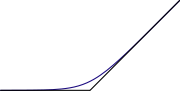
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
. However, it presents a perpetual difficulty in numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, essentially since "max" is not invertible. If b is much greater than a, then a straightforward calculation of (a + b) − b can accumulate an unacceptable round-off error
Round-off error
A round-off error, also called rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. Numerical analysis specifically tries to estimate this error when using approximation equations and/or algorithms, especially when using finitely many...
, perhaps even returning zero. See also Loss of significance
Loss of significance
Loss of significance is an undesirable effect in calculations using floating-point arithmetic. It occurs when an operation on two numbers increases relative error substantially more than it increases absolute error, for example in subtracting two large and nearly equal numbers. The effect is that...
.
The approximation becomes exact in a kind of infinite limit; if either a or b is an infinite cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
, their cardinal sum is exactly equal to the greater of the two. Accordingly, there is no subtraction operation for infinite cardinals.
Maximization is commutative and associative, like addition. Furthermore, since addition preserves the ordering of real numbers, addition distributes over "max" in the same way that multiplication distributes over addition:
- a + max (b, c) = max (a + b, a + c).
For these reasons, in tropical geometry
Tropical geometry
Tropical geometry is a relatively new area in mathematics, which might loosely be described as a piece-wise linear or skeletonized version of algebraic geometry. Its leading ideas had appeared in different guises in previous works of George M...
one replaces multiplication with addition and addition with maximization. In this context, addition is called "tropical multiplication", maximization is called "tropical addition", and the tropical "additive identity" is negative infinity
Extended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
. Some authors prefer to replace addition with minimization; then the additive identity is positive infinity.
Tying these observations together, tropical addition is approximately related to regular addition through the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
:
- log (a + b) ≈ max (log a, log b),
which becomes more accurate as the base of the logarithm increases. The approximation can be made exact by extracting a constant h, named by analogy with Planck's constant from quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, and taking the "classical limit
Classical limit
The classical limit or correspondence limit is the ability of a physical theory to approximate or "recover" classical mechanics when considered over special values of its parameters. The classical limit is used with physical theories that predict non-classical behavior...
" as h tends to zero:
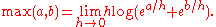
In this sense, the maximum operation is a dequantized version of addition.
Other ways to add
Incrementation, also known as the successorPrimitive recursive function
The primitive recursive functions are defined using primitive recursion and composition as central operations and are a strict subset of the total µ-recursive functions...
operation, is the addition of 1 to a number.
Summation
Summation
Summation is the operation of adding a sequence of numbers; the result is their sum or total. If numbers are added sequentially from left to right, any intermediate result is a partial sum, prefix sum, or running total of the summation. The numbers to be summed may be integers, rational numbers,...
describes the addition of arbitrarily many numbers, usually more than just two. It includes the idea of the sum of a single number, which is itself, and the empty sum
Empty sum
In mathematics, an empty sum, or nullary sum, is a summation involving no terms at all. The value of any empty sum of numbers is conventionally taken to be zero...
, which is zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
. An infinite summation is a delicate procedure known as a series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
.
Counting
Counting
Counting is the action of finding the number of elements of a finite set of objects. The traditional way of counting consists of continually increasing a counter by a unit for every element of the set, in some order, while marking those elements to avoid visiting the same element more than once,...
a finite set is equivalent to summing 1 over the set.
Integration
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
is a kind of "summation" over a continuum, or more precisely and generally, over a differentiable
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
. Integration over a zero-dimensional manifold reduces to summation.
Linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
s combine multiplication and summation; they are sums in which each term has a multiplier, usually a real or complex number. Linear combinations are especially useful in contexts where straightforward addition would violate some normalization rule, such as mixing of strategies
Strategy (game theory)
In game theory, a player's strategy in a game is a complete plan of action for whatever situation might arise; this fully determines the player's behaviour...
in game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
or superposition
Quantum superposition
Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...
of states in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
Convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
is used to add two independent random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s defined by distribution functions
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
. Its usual definition combines integration, subtraction, and multiplication. In general, convolution is useful as a kind of domain-side addition; by contrast, vector addition is a kind of range-side addition.
In literature
- In chapter 9 of Lewis CarrollLewis CarrollCharles Lutwidge Dodgson , better known by the pseudonym Lewis Carroll , was an English author, mathematician, logician, Anglican deacon and photographer. His most famous writings are Alice's Adventures in Wonderland and its sequel Through the Looking-Glass, as well as the poems "The Hunting of the...
's Through the Looking-GlassThrough the Looking-GlassThrough the Looking-Glass, and What Alice Found There is a work of literature by Lewis Carroll . It is the sequel to Alice's Adventures in Wonderland...
, the White Queen asks Alice, "And you do Addition? ... What's one and one and one and one and one and one and one and one and one and one?" Alice admits that she lost count, and the Red Queen declares, "She can't do Addition". - In George OrwellGeorge OrwellEric Arthur Blair , better known by his pen name George Orwell, was an English author and journalist...
's Nineteen Eighty-FourNineteen Eighty-FourNineteen Eighty-Four by George Orwell is a dystopian novel about Oceania, a society ruled by the oligarchical dictatorship of the Party...
, the value of 2 + 2 is questioned; the State contends that if it declares 2 + 2 = 5, then it is so. See Two plus two make five for the history of this idea.

