
Total order
Encyclopedia
In set theory
, a total order, linear order, simple order, or (non-strict) ordering is a binary relation
(here denoted by infix
≤) on some set X. The relation is transitive
, antisymmetric
, and total
. A set paired with a total order is called a totally ordered set, a linearly ordered set, a simply ordered set, or a chain.
If X is totally ordered under ≤, then the following statements hold for all a, b and c in X:
Contrast with a partial order, which has a weaker form of the third condition (it only requires reflexivity
, not totality).
A relation having the property of "totality" means that any pair of elements in the set of the relation are mutually comparable under the relation. Totality implies reflexivity, that is, a ≤ a, thus a total order is also a partial order. An extension of a given partial order to a total order is called a linear extension
of that partial order.
(hence irreflexive) relation <, called a strict total order, which can equivalently be defined in two ways:
Properties:
We can work the other way and start by choosing < as a transitive trichotomous binary relation; then a total order ≤ can equivalently be defined in two ways:
Two more associated orders are the complements ≥ and >, completing the quadruple
{<, >, ≤, ≥}.
We can define or explain the way a set is totally ordered by any of these four relations; the notation implies whether we are talking about the non-strict or the strict total order.
of some partially ordered set
. The latter definition has a crucial role in Zorn's lemma
.
For example, consider the set of all subsets of the integer
s partially ordered by inclusion
. Then the set { In : n is a natural number
}, where In is the set of natural numbers below n, is a chain in this ordering, as it is totally ordered under inclusion: If n≤k, then In is a subset of Ik.
, namely one in which we have
We then write a ≤ b if and only if
 . Hence a totally ordered set is a distributive lattice
. Hence a totally ordered set is a distributive lattice
.
argument will verify that any non-empty finite totally-ordered set (and hence any non-empty subset thereof) has a least element. Thus every finite total order is in fact a well order. Either by direct proof or by observing that every well order is order isomorphic to an ordinal
one may show that every finite total order is order isomorphic to an initial segment of the natural numbers ordered by <. In other words a total order on a set with k elements induces a bijection with the first k natural numbers. Hence it is common to index finite total orders or well orders with order type
ω by natural numbers in a fashion which respects the ordering (either starting with zero or with one).
of the category
of partially ordered set
s, with the morphism
s being maps which respect the orders, i.e. maps f such that if a ≤ b then f(a) ≤ f(b).
A bijective
map
between two totally ordered sets that respects the two orders is an isomorphism
in this category.
s (a, b) = {x : a < x and x < b}, (−∞, b) = {x : x < b}, (a, ∞) = {x : a < x} and (−∞, ∞) = X. We can use these open intervals to define a topology
on any ordered set, the order topology
.
When more than one order is being used on a set one talks about the order topology induced by a particular order. For instance if N is the natural numbers, < is less than and > greater than we might refer to the order topology on N induced by < and the order topology on N induced by > (in this case they happen to be identical but will not in general).
The order topology induced by a total order may be shown to be hereditarily normal
.
, has a least upper bound. For example, the set of real number
s R is complete but the set of rational number
s Q is not.
There are a number of results relating properties of the order topology to the completeness of X:
A totally ordered set (with its order topology) which is a complete lattice
is compact
. Examples are the closed intervals of real numbers, e.g. the unit interval
[0,1], and the affinely extended real number system (extended real number line). There are order-preserving homeomorphism
s between these examples.
 and
and  , there is a natural order
, there is a natural order  on the set
on the set  , which is called the sum of the two orders or sometimes just
, which is called the sum of the two orders or sometimes just  :
:
Intutitively, this means that the elements of the second set are added on top of the elements of the first set.
More generally, if is a totally ordered index set, and for each
is a totally ordered index set, and for each  the structure
the structure  is a linear order, where the sets
is a linear order, where the sets 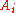 are pairwise disjoint, then the natural total order on
are pairwise disjoint, then the natural total order on 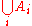 is defined by
is defined by
of two totally ordered sets are:
All three can similarly be defined for the Cartesian product of more than two sets.
Applied to the vector space
Rn, each of these make it an ordered vector space
.
See also examples of partially ordered sets.
A real function of n real variables defined on a subset of Rn defines a strict weak order and a corresponding total preorder on that subset.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a total order, linear order, simple order, or (non-strict) ordering is a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
(here denoted by infix
Infix notation
Infix notation is the common arithmetic and logical formula notation, in which operators are written infix-style between the operands they act on . It is not as simple to parse by computers as prefix notation or postfix notation Infix notation is the common arithmetic and logical formula notation,...
≤) on some set X. The relation is transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
, antisymmetric
Antisymmetric relation
In mathematics, a binary relation R on a set X is antisymmetric if, for all a and b in Xor, equivalently,In mathematical notation, this is:\forall a, b \in X,\ R \and R \; \Rightarrow \; a = bor, equivalently,...
, and total
Total relation
In mathematics, a binary relation R over a set X is total if for all a and b in X, a is related to b or b is related to a .In mathematical notation, this is\forall a, b \in X,\ a R b \or b R a....
. A set paired with a total order is called a totally ordered set, a linearly ordered set, a simply ordered set, or a chain.
If X is totally ordered under ≤, then the following statements hold for all a, b and c in X:
- If a ≤ b and b ≤ a then a = b (antisymmetryAntisymmetric relationIn mathematics, a binary relation R on a set X is antisymmetric if, for all a and b in Xor, equivalently,In mathematical notation, this is:\forall a, b \in X,\ R \and R \; \Rightarrow \; a = bor, equivalently,...
); - If a ≤ b and b ≤ c then a ≤ c (transitivityTransitive relationIn mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
); - a ≤ b orLogical disjunctionIn logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
b ≤ a (totalityTotal relationIn mathematics, a binary relation R over a set X is total if for all a and b in X, a is related to b or b is related to a .In mathematical notation, this is\forall a, b \in X,\ a R b \or b R a....
).
Contrast with a partial order, which has a weaker form of the third condition (it only requires reflexivity
Reflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
, not totality).
A relation having the property of "totality" means that any pair of elements in the set of the relation are mutually comparable under the relation. Totality implies reflexivity, that is, a ≤ a, thus a total order is also a partial order. An extension of a given partial order to a total order is called a linear extension
Linear extension
In order theory, a branch of mathematics, a linear extension of a partial order is a linear order that is compatible with the partial order.-Definitions:...
of that partial order.
Strict total order
For each (non-strict) total order ≤ there is an associated asymmetricAsymmetric relation
Asymmetric often means, simply: not symmetric. In this sense an asymmetric relation is a binary relation which is not a symmetric relation.That is,\lnot....
(hence irreflexive) relation <, called a strict total order, which can equivalently be defined in two ways:
- a < b if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
a ≤ b and a ≠ b - a < b if and only if not b ≤ a (i.e., < is the inverse of the complement of ≤)
Properties:
- The relation is transitive: a < b and b < c implies a < c.
- The relation is trichotomous: exactly one of a < b, b < a and a = b is true.
- The relation is a strict weak order, where the associated equivalence is equality.
We can work the other way and start by choosing < as a transitive trichotomous binary relation; then a total order ≤ can equivalently be defined in two ways:
- a ≤ b if and only if a < b or a = b
- a ≤ b if and only if not b < a
Two more associated orders are the complements ≥ and >, completing the quadruple
Quadruple
Quadruple may refer to:* Tuple, a mathematical structure* Quadruple, a term for winning four association trophies* Quad , a figure skating jump* Home run in baseball* Quadruple-precision floating-point format in computing...
{<, >, ≤, ≥}.
We can define or explain the way a set is totally ordered by any of these four relations; the notation implies whether we are talking about the non-strict or the strict total order.
Examples
- The letters of the alphabet ordered by the standard dictionary order, e.g., A < B < C etc.
- Any subset of a totally ordered set, with the restriction of the order on the whole set.
- Any set of cardinal numberCardinal numberIn mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s or ordinal numberOrdinal numberIn set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
s (more strongly, these are well-orderWell-orderIn mathematics, a well-order relation on a set S is a strict total order on S with the property that every non-empty subset of S has a least element in this ordering. Equivalently, a well-ordering is a well-founded strict total order...
s).
- If X is any set and f an injective functionInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
from X to a totally ordered set then f induces a total ordering on X by setting x1 < x2 if and only if f(x1) < f(x2).
- The lexicographical orderLexicographical orderIn mathematics, the lexicographic or lexicographical order, , is a generalization of the way the alphabetical order of words is based on the alphabetical order of letters.-Definition:Given two partially ordered sets A and B, the lexicographical order on...
on the Cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of a set of totally ordered sets indexed by an ordinal, is itself a total order. For example, any set of words ordered alphabetically is a totally ordered set, viewed as a subset of a Cartesian product of a countable number of copies of a set formed by adding the space symbol to the alphabet (and defining a space to be less than any letter).
- The set of real numbers ordered by the usual less than (<) or greater than (>) relations is totally ordered, hence also the subsets of natural numbers, integers, and rational numbers. Each of these can be shown to be the unique (to within isomorphism) smallest example of a totally ordered set with a certain property, (a total order A is the smallest with a certain property if whenever B has the property, there is an order isomorphism from A to a subset of B):
- The natural numbers comprise the smallest totally ordered set with no upper boundUpper boundIn mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
. - The integers comprise the smallest totally ordered set with neither an upper nor a lower bound.
- The rational numbers comprise the smallest totally ordered set with no upper or lower bound, which is denseDense orderIn mathematics, a partial order ≤ on a set X is said to be dense if, for all x and y in X for which x In mathematics, a partial order ≤ on a set X is said to be dense if, for all x and y in X for which x...
in the sense that for every a and b such that a < b there is a c such that a < c < b. - The real numbers comprise the smallest unbounded connectedConnectednessIn mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...
totally ordered set. (See below for the definition of the topology.)
- The natural numbers comprise the smallest totally ordered set with no upper bound
Chains
While chain is sometimes merely a synonym for totally ordered set, it can also refer to a totally ordered subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of some partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
. The latter definition has a crucial role in Zorn's lemma
Zorn's lemma
Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
.
For example, consider the set of all subsets of the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s partially ordered by inclusion
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
. Then the set { In : n is a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
}, where In is the set of natural numbers below n, is a chain in this ordering, as it is totally ordered under inclusion: If n≤k, then In is a subset of Ik.
Lattice theory
One may define a totally ordered set as a particular kind of latticeLattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
, namely one in which we have
-
 for all a, b.
for all a, b.
We then write a ≤ b if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
 . Hence a totally ordered set is a distributive lattice
. Hence a totally ordered set is a distributive latticeDistributive lattice
In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
.
Finite total orders
A simple countingCounting
Counting is the action of finding the number of elements of a finite set of objects. The traditional way of counting consists of continually increasing a counter by a unit for every element of the set, in some order, while marking those elements to avoid visiting the same element more than once,...
argument will verify that any non-empty finite totally-ordered set (and hence any non-empty subset thereof) has a least element. Thus every finite total order is in fact a well order. Either by direct proof or by observing that every well order is order isomorphic to an ordinal
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
one may show that every finite total order is order isomorphic to an initial segment of the natural numbers ordered by <. In other words a total order on a set with k elements induces a bijection with the first k natural numbers. Hence it is common to index finite total orders or well orders with order type
Order type
In mathematics, especially in set theory, two ordered sets X,Y are said to have the same order type just when they are order isomorphic, that is, when there exists a bijection f: X → Y such that both f and its inverse are monotone...
ω by natural numbers in a fashion which respects the ordering (either starting with zero or with one).
Category theory
Totally ordered sets form a full subcategorySubcategory
In mathematics, a subcategory of a category C is a category S whose objects are objects in C and whose morphisms are morphisms in C with the same identities and composition of morphisms. Intuitively, a subcategory of C is a category obtained from C by "removing" some of its objects and...
of the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
s, with the morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s being maps which respect the orders, i.e. maps f such that if a ≤ b then f(a) ≤ f(b).
A bijective
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
map
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
between two totally ordered sets that respects the two orders is an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
in this category.
Order topology
For any totally ordered set X we can define the open intervalInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
s (a, b) = {x : a < x and x < b}, (−∞, b) = {x : x < b}, (a, ∞) = {x : a < x} and (−∞, ∞) = X. We can use these open intervals to define a topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
on any ordered set, the order topology
Order topology
In mathematics, an order topology is a certain topology that can be defined on any totally ordered set. It is a natural generalization of the topology of the real numbers to arbitrary totally ordered sets...
.
When more than one order is being used on a set one talks about the order topology induced by a particular order. For instance if N is the natural numbers, < is less than and > greater than we might refer to the order topology on N induced by < and the order topology on N induced by > (in this case they happen to be identical but will not in general).
The order topology induced by a total order may be shown to be hereditarily normal
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
.
Completeness
A totally ordered set is said to be complete if every nonempty subset that has an upper boundUpper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
, has a least upper bound. For example, the set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s R is complete but the set of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s Q is not.
There are a number of results relating properties of the order topology to the completeness of X:
- If the order topology on X is connected, X is complete.
- X is connected under the order topology if and only if it is complete and there is no gap in X (a gap is two points a and b in X with a < b such that no c satisfies a < c < b.)
- X is complete if and only if every bounded set that is closed in the order topology is compact.
A totally ordered set (with its order topology) which is a complete lattice
Complete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
. Examples are the closed intervals of real numbers, e.g. the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
[0,1], and the affinely extended real number system (extended real number line). There are order-preserving homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
s between these examples.
Sums of orders
For any two disjoint total orders and
and  , there is a natural order
, there is a natural order  on the set
on the set  , which is called the sum of the two orders or sometimes just
, which is called the sum of the two orders or sometimes just  :
:
- For
 ,
,  holds if and only if one of the following holds:
holds if and only if one of the following holds:
-
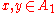 and
and 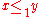
-
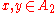 and
and 
-
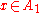 and
and 
-
Intutitively, this means that the elements of the second set are added on top of the elements of the first set.
More generally, if
 is a totally ordered index set, and for each
is a totally ordered index set, and for each  the structure
the structure  is a linear order, where the sets
is a linear order, where the sets 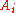 are pairwise disjoint, then the natural total order on
are pairwise disjoint, then the natural total order on 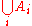 is defined by
is defined by
- For
 ,
,  holds if:
holds if:
- Either there is some
 with
with 
- or there are some
 in
in  with
with  ,
, 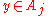
- Either there is some
Orders on the Cartesian product of totally ordered sets
In order of increasing strength, i.e., decreasing sets of pairs, three of the possible orders on the Cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of two totally ordered sets are:
- Lexicographical orderLexicographical orderIn mathematics, the lexicographic or lexicographical order, , is a generalization of the way the alphabetical order of words is based on the alphabetical order of letters.-Definition:Given two partially ordered sets A and B, the lexicographical order on...
: (a,b) ≤ (c,d) if and only if a < c or (a = c and b ≤ d). This is a total order. - (a,b) ≤ (c,d) if and only if a ≤ c and b ≤ d (the product orderProduct orderIn mathematics, given two ordered sets A and B, one can induce a partial ordering on the Cartesian product A × B. Giventwo pairs and in A × B, one sets ≤...
). This is a partial order. - (a,b) ≤ (c,d) if and only if (a < c and b < d) or (a = c and b = d) (the reflexive closure of the direct product of the corresponding strict total orders). This is also a partial order.
All three can similarly be defined for the Cartesian product of more than two sets.
Applied to the vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
Rn, each of these make it an ordered vector space
Ordered vector space
In mathematics an ordered vector space or partially ordered vector space is a vector space equipped with a partial order which is compatible with the vector space operations.- Definition:...
.
See also examples of partially ordered sets.
A real function of n real variables defined on a subset of Rn defines a strict weak order and a corresponding total preorder on that subset.

