
Analytic geometry
Encyclopedia

Analytic variety
In mathematics, specifically geometry, an analytic variety is defined locally as the set of common zeros of finitely many analytic functions. It is analogous to the included concept of complex algebraic variety, and every complex manifold is an analytic variety. Since analytic varieties may have...
. This article focuses on the classical and elementary meaning.
In classical mathematics, analytic geometry, also known as coordinate geometry, or Cartesian geometry, is the study of geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
using a coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
and the principles of algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
and analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
. This contrasts with the synthetic
Synthetic geometry
Synthetic or axiomatic geometry is the branch of geometry which makes use of axioms, theorems and logical arguments to draw conclusions, as opposed to analytic and algebraic geometries which use analysis and algebra to perform geometric computations and solve problems.-Logical synthesis:The process...
approach of Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, which treats certain geometric notions as primitive
Primitive notion
In mathematics, logic, and formal systems, a primitive notion is an undefined concept. In particular, a primitive notion is not defined in terms of previously defined concepts, but is only motivated informally, usually by an appeal to intuition and everyday experience. In an axiomatic theory or...
, and uses deductive reasoning
Deductive reasoning
Deductive reasoning, also called deductive logic, is reasoning which constructs or evaluates deductive arguments. Deductive arguments are attempts to show that a conclusion necessarily follows from a set of premises or hypothesis...
based on axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s and theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
s to derive truth. Analytic geometry is widely used in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, and is the foundation of most modern fields of geometry, including algebraic
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, differential, discrete
Discrete geometry
Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles,...
, and computational
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
geometry.
Usually the Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
is applied to manipulate equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
s for plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
s, straight line
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
s, and square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
s, often in two and sometimes in three dimensions of measurement. Geometrically, one studies the Euclidean plane (2 dimensions) and Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
(3 dimensions). As taught in school books, analytic geometry can be explained more simply: it is concerned with defining and representing geometrical shapes in a numerical way and extracting numerical information from shapes' numerical definitions and representations. The numerical output, however, might also be a vector or a shape. That the algebra of the real numbers can be employed to yield results about the linear continuum of geometry relies on the Cantor–Dedekind axiom.
History
The GreekAncient Greece
Ancient Greece is a civilization belonging to a period of Greek history that lasted from the Archaic period of the 8th to 6th centuries BC to the end of antiquity. Immediately following this period was the beginning of the Early Middle Ages and the Byzantine era. Included in Ancient Greece is the...
mathematician Menaechmus
Menaechmus
Menaechmus was an ancient Greek mathematician and geometer born in Alopeconnesus in the Thracian Chersonese, who was known for his friendship with the renowned philosopher Plato and for his apparent discovery of conic sections and his solution to the then-long-standing problem of doubling the cube...
solved problems and proved theorems by using a method that had a strong resemblance to the use of coordinates and it has sometimes been maintained that he had introduced analytic geometry. Apollonius of Perga
Apollonius of Perga
Apollonius of Perga [Pergaeus] was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Isaac Newton, and René Descartes...
, in On Determinate Section, dealt with problems in a manner that may be called an analytic geometry of one dimension; with the question of finding points on a line that were in a ratio to the others. Apollonius in the Conics further developed a method that is so similar to analytic geometry that his work is sometimes thought to have anticipated the work of Descartes — by some 1800 years. His application of reference lines, a diameter and a tangent is essentially no different than our modern use of a coordinate frame, where the distances measured along the diameter from the point of tangency are the abscissas, and the segments parallel to the tangent and intercepted between the axis and the curve are the ordinates. He further developed relations between the abscissas and the corresponding ordinates that are equivalent to rhetorical equations of curves. However, although Apollonius came close to developing analytic geometry, he did not manage to do so since he did not take into account negative magnitudes and in every case the coordinate system was superimposed upon a given curve a posteriori instead of a priori. That is, equations were determined by curves, but curves were not determined by equations. Coordinates, variables, and equations were subsidiary notions applied to a specific geometric situation.
The eleventh century Persian mathematician Omar Khayyám
Omar Khayyám
Omar Khayyám was aPersian polymath: philosopher, mathematician, astronomer and poet. He also wrote treatises on mechanics, geography, mineralogy, music, climatology and theology....
saw a strong relationship between geometry and algebra, and was moving in the right direction when he helped to close the gap between numerical and geometric algebra with his geometric solution of the general cubic equations, but the decisive step came later with Descartes.
Analytic geometry has traditionally been attributed to René Descartes
René Descartes
René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
Descartes made significant progress with the methods in an essay entitled Geometry
La Géométrie
La Géométrie was published in 1637 as an appendix to Discours de la méthode , written by René Descartes. In the Discourse, he presents his method for obtaining clarity on any subject...
, one of the three accompanying essays published in 1637 together with his Discourse on the Method of Rightly Conducting the Reason in the Search for Truth in the Sciences, commonly referred to as Discourse on Method
Discourse on Method
The Discourse on the Method is a philosophical and autobiographical treatise published by René Descartes in 1637. Its full name is Discourse on the Method of Rightly Conducting One's Reason and of Seeking Truth in the Sciences .The Discourse on Method is best known...
. This work, written in his native French
French language
French is a Romance language spoken as a first language in France, the Romandy region in Switzerland, Wallonia and Brussels in Belgium, Monaco, the regions of Quebec and Acadia in Canada, and by various communities elsewhere. Second-language speakers of French are distributed throughout many parts...
tongue, and its philosophical principles, provided the foundation for Infinitesimal calculus
Infinitesimal calculus
Infinitesimal calculus is the part of mathematics concerned with finding slope of curves, areas under curves, minima and maxima, and other geometric and analytic problems. It was independently developed by Gottfried Leibniz and Isaac Newton starting in the 1660s...
in Europe.
Abraham de Moivre
Abraham de Moivre
Abraham de Moivre was a French mathematician famous for de Moivre's formula, which links complex numbers and trigonometry, and for his work on the normal distribution and probability theory. He was a friend of Isaac Newton, Edmund Halley, and James Stirling...
also pioneered the development of analytic geometry.
Basic principles
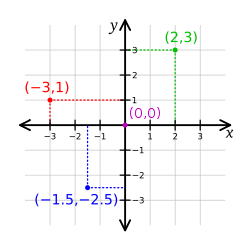
Coordinates
In analytic geometry, the plane is given a coordinate system, by which every pointPoint (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
has a pair of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
coordinates. The most common coordinate system to use is the Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
, where each point has an x-coordinate representing its horizontal position, and a y-coordinate representing its vertical position. These are typically written as an ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
(x, y). This system can also be used for three-dimensional geometry, where every point in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
is represented by an ordered triple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
of coordinates (x, y, z).
Other coordinate systems are possible. On the plane the most common alternative is polar coordinates, where every point is represented by its radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
r from the origin and its angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
θ. In three dimensions, common alternative coordinate systems include cylindrical coordinates and spherical coordinates.
Equations of curves
In analytic geometry, any equationEquation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
involving the coordinates specifies a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of the plane, namely the solution set for the equation. For example, the equation y = x corresponds to the set of all the points on the plane whose x-coordinate and y-coordinate are equal. These points form a line
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
, and y = x is said to be the equation for this line. In general, linear equations involving x and y specify lines, quadratic equation
Quadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
s specify conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
s, and more complicated equations describe more complicated figures.
Usually, a single equation corresponds to a curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
on the plane. This is not always the case: the trivial equation x = x specifies the entire plane, and the equation x2 + y2 = 0 specifies only the single point (0, 0). In three dimensions, a single equation usually gives a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
, and a curve must be specified as the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of two surfaces (see below), or as a system of parametric equation
Parametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
s. The equation x2 + y2 = r2 is the equation for any circle with a radius of r.
Distance and angle
In analytic geometry, geometric notions such as distanceDistance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
and angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
measure are defined using formula
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
s. These definitions are designed to be consistent with the underlying Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
. For example, using Cartesian coordinates on the plane, the distance between two points (x1, y1) and (x2, y2) is defined by the formula
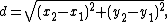
which can be viewed as a version of the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
. Similarly, the angle that a line makes with the horizontal can be defined by the formula
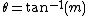
where m is the slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
of the line.
Section of a Line
In Analytical Geometry a section of a line can be given by the formula where (c,d)&(e,f) are the endpoints of the line & m:n is the ratio of divisionS(a,b)=(nc+me/m+n , nd+mf/m+n)
Transformations
Transformations are applied to parent functions to turn it into a new function with similar characteristics. For example, the parent function y=1/x has a horizontal and a vertical asymptote, and occupies the first and third quadrant, and all of its transformed forms have one horizontal and vertical asymptote,and occupies either the 1st and 3rd or 2nd and 4th quadrant. In general, if y = f(x), then it can be transformed into y = af(b(x − k)) + h. In the new transformed function, a is the factor that vertically stretches the function if it is greater than 1 or vertically compresses the function if it is less than 1, and for negative a values, the function is reflected in the x-axis. The b value compresses the graph of the function horizontally if greater than 1 and stretches the function horizontally if less than 1, and like a, reflects the function in the y-axis when it is negative. The k and h values introduce translations, h, vertical, and k horizontal. Positive h and k values mean the function is translated to the positive end of its axis and negative meaning translation towards the negative end.Themes
Important themes of analytical geometry are- vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
- definition of the planePlane (mathematics)In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
- distanceDistanceDistance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
problems - the dot productDot productIn mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
, to get the angle of two vectors - the cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
, to get a perpendicular vector of two known vectors (and also their spatial volume) - intersectionIntersection (set theory)In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
problems
Many of these problems involve linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
.
Example
Here an example of a problem from the United States of America Mathematical Talent SearchUnited States of America Mathematical Talent Search
The United States of America Mathematical Talent Search is a mathematics competition open to all United States students in or below high school.-History of contest:...
that can be solved via analytic geometry:
Problem: In a convex pentagon
 , the sides have lengths
, the sides have lengths 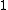 ,
, 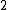 ,
, 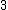 ,
, 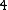 , and
, and 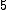 , though not necessarily in
, though not necessarily inthat order. Let
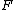 ,
, 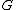 ,
,  , and
, and 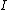 be the midpoints of the sides
be the midpoints of the sides 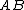 ,
, 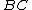 ,
, 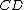 , and
, and 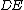 , respectively.
, respectively.Let
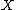 be the midpoint of segment
be the midpoint of segment 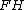 , and
, and 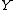 be the midpoint of segment
be the midpoint of segment 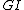 . The length of
. The length ofsegment
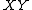 is an integer. Find all possible values for the length of side
is an integer. Find all possible values for the length of side 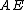 .
.Solution: Without loss of generality
Without loss of generality
Without loss of generality is a frequently used expression in mathematics...
, let
 ,
,  ,
,  ,
, 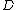 , and
, and 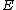 be located at
be located at 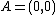 ,
, 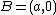 ,
, 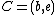 ,
, 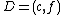 , and
, and 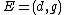 .
.Using the midpoint
Midpoint
The midpoint is the middle point of a line segment. It is equidistant from both endpoints.-Formulas:...
formula, the points
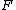 ,
, 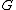 ,
, 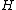 ,
,  ,
,  , and
, and 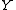 are located at
are located at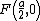 ,
,  ,
, 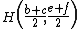 ,
, 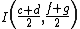 ,
, 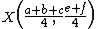 , and
, and 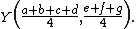
Using the distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
formula,
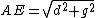
and
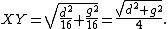
Since
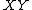 has to be an integer
has to be an integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
,
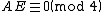
(see modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
) so
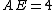 .
.Modern analytic geometry
An analytic varietyAnalytic variety
In mathematics, specifically geometry, an analytic variety is defined locally as the set of common zeros of finitely many analytic functions. It is analogous to the included concept of complex algebraic variety, and every complex manifold is an analytic variety. Since analytic varieties may have...
is defined locally as the set of common solutions of several equations involving analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s. It is analogous to the included concept of real or complex algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
. Any complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
is an analytic variety. Since analytic varieties may have singular points
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
, not all analytic varieties are manifolds.
Analytic geometry is essentially equivalent to real and complex Algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, as has been shown by Jean-Pierre Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
in his paper GAGA
Gaga
- Entertainment :* Lady Gaga , American recording artist* Gaga , a dancing technique* Rara, a type of Caribbean music called Gaga in the Dominican Republic* GNZ-004 Gaga, a mobile weapon in Mobile Suit Gundam 00- Sports :...
, the name of which is French for Algebraic geometry and analytic geometry. Nevertheless, the two fields remain distinct, as the methods of proof are quite different and algebraic geometry includes also geometry in finite characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
.
External links
- Coordinate Geometry topics with interactive animations

