Group theory
Encyclopedia
In mathematics
and abstract algebra
, group theory studies the algebraic structure
s known as groups
.
The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings
, fields
, and vector space
s can all be seen as groups endowed with additional operation
s and axiom
s. Groups recur throughout mathematics, and the methods of group theory have strongly influenced many parts of algebra. Linear algebraic group
s and Lie group
s are two branches of group theory that have experienced tremendous advances and have become subject areas in their own right.
Various physical systems, such as crystal
s and the hydrogen atom
, can be modelled by symmetry group
s. Thus group theory and the closely related representation theory
have many applications in physics
and chemistry
.
One of the most important mathematical achievements of the 20th century was the collaborative effort, taking up more than 10,000 journal pages and mostly published between 1960 and 1980, that culminated in a complete classification of finite simple groups
.
, the theory of algebraic equations, and geometry
. The number-theoretic strand was begun by Leonhard Euler
, and developed by Gauss
's work on modular arithmetic
and additive and multiplicative groups related to quadratic field
s. Early results about permutation group
s were obtained by Lagrange
, Ruffini
, and Abel
in their quest for general solutions of polynomial equations of high degree. Évariste Galois
coined the term "group" and established a connection, now known as Galois theory
, between the nascent theory of groups and field theory
. In geometry, groups first became important in projective geometry
and, later, non-Euclidean geometry
. Felix Klein
's Erlangen program
proclaimed group theory to be the organizing principle of geometry.
Galois
, in the 1830s, was the first to employ groups to determine the solvability of polynomial equations. Arthur Cayley
and Augustin Louis Cauchy
pushed these investigations further by creating the theory of permutation group
. The second historical source for groups stems from geometrical
situations. In an attempt to come to grips with possible geometries (such as euclidean
, hyperbolic
or projective geometry
) using group theory, Felix Klein
initiated the Erlangen programme. Sophus Lie
, in 1884, started using groups (now called Lie group
s) attached to analytic problems. Thirdly, groups were (first implicitly and later explicitly) used in algebraic number theory
.
The different scope of these early sources resulted in different notions of groups. The theory of groups was unified starting around 1880. Since then, the impact of group theory has been ever growing, giving rise to the birth of abstract algebra
in the early 20th century, representation theory
, and many more influential spin-off domains. The classification of finite simple groups
is a vast body of work from the mid 20th century, classifying all the finite simple group
s.
s and special examples of matrix group
s to abstract groups that may be specified through a presentation
by generators and relations.
s. Given any set X and a collection G of bijection
s of X into itself (known as permutations) that is closed under compositions and inverses, G is a group acting
on X. If X consists of n elements and G consists of all permutations, G is the symmetric group
Sn; in general, any permutation group G is a subgroup
of the symmetric group of X. An early construction due to Cayley
exhibited any group as a permutation group, acting on itself (X = G) by means of the left regular representation
.
In many cases, the structure of a permutation group can be studied using the properties of its action on the corresponding set. For example, in this way one proves that for n ≥ 5, the alternating group An is simple
, i.e. does not admit any proper normal subgroup
s. This fact plays a key role in the impossibility of solving a general algebraic equation of degree n ≥ 5 in radicals
.
of given order n over a field
K that is closed under the products and inverses. Such a group acts on the n-dimensional vector space Kn by linear transformation
s. This action makes matrix groups conceptually similar to permutation groups, and the geometry of the action may be usefully exploited to establish properties of the group G.
. The concept of a transformation group is closely related with the concept of a symmetry group
: transformation groups frequently consist of all transformations that preserve a certain structure.
The theory of transformation groups forms a bridge connecting group theory with differential geometry. A long line of research, originating with Lie
and Klein
, considers group actions on manifold
s by homeomorphism
s or diffeomorphism
s. The groups themselves may be discrete
or continuous.
by generators and relations,
A significant source of abstract groups is given by the construction of a factor group, or quotient group
, G/H, of a group G by a normal subgroup
H. Class groups of algebraic number field
s were among the earliest examples of factor groups, of much interest in number theory
. If a group G is a permutation group on a set X, the factor group G/H is no longer acting on X; but the idea of an abstract group permits one not to worry about this discrepancy.
The change of perspective from concrete to abstract groups makes it natural to consider properties of groups that are independent of a particular realization, or in modern language, invariant under isomorphism
, as well as the classes of group with a given such property: finite group
s, periodic group
s, simple group
s, solvable group
s, and so on. Rather than exploring properties of an individual group, one seeks to establish results that apply to a whole class of groups. The new paradigm was of paramount importance for the development of mathematics: it foreshadowed the creation of abstract algebra
in the works of Hilbert
, Emil Artin
, Emmy Noether
, and mathematicians of their school.
, differentiable manifold
, or algebraic variety
. If the group operations m (multiplication) and i (inversion),
are compatible with this structure, i.e. are continuous, smooth or regular
(in the sense of algebraic geometry) maps then G becomes a topological group
, a Lie group
, or an algebraic group
.
The presence of extra structure relates these types of groups with other mathematical disciplines and means that more tools are available in their study. Topological groups form a natural domain for abstract harmonic analysis, whereas Lie group
s (frequently realized as transformation groups) are the mainstays of differential geometry and unitary representation theory
. Certain classification questions that cannot be solved in general can be approached and resolved for special subclasses of groups. Thus, compact connected Lie groups have been completely classified. There is a fruitful relation between infinite abstract groups and topological groups: whenever a group Γ can be realized as a lattice
in a topological group G, the geometry and analysis pertaining to G yield important results about Γ. A comparatively recent trend in the theory of finite groups exploits their connections with compact topological groups (profinite groups): for example, a single p-adic analytic group
G has a family of quotients which are finite p-groups
of various orders, and properties of G translate into the properties of its finite quotients.
generated by F surjects onto the group G. The kernel of this map is called subgroup of relations, generated by some subset D. The presentation is usually denoted by 〈F | D 〉. For example, the group Z = 〈a | 〉 can be generated by one element a (equal to +1 or −1) and no relations, because n·1 never equals 0 unless n is zero. A string consisting of generator symbols and their inverses is called a word.
Combinatorial group theory
studies groups from the perspective of generators and relations. It is particularly useful where finiteness assumptions are satisfied, for example finitely generated groups, or finitely presented groups (i.e. in addition the relations are finite). The area makes use of the connection of graphs
via their fundamental group
s. For example, one can show that every subgroup of a free group is free.
There are several natural questions arising from giving a group by its presentation. The word problem
asks whether two words are effectively the same group element. By relating the problem to Turing machine
s, one can show that there is in general no algorithm
solving this task. An equally difficult problem is, whether two groups given by different presentations are actually isomorphic. For example Z can also be presented by
and it is not obvious (but true) that this presentation is isomorphic to the standard one above.
 Geometric group theory
Geometric group theory
attacks these problems from a geometric viewpoint, either by viewing groups as geometric objects, or by finding suitable geometric objects a group acts on. The first idea is made precise by means of the Cayley graph
, whose vertices correspond to group elements and edges correspond to right multiplication in the group. Given two elements, one constructs the word metric given by the length of the minimal path between the elements. A theorem of Milnor
and Svarc then says that given a group G acting in a reasonable manner on a metric space
X, for example a compact manifold, then G is quasi-isometric
(i.e. looks similar from the far) to the space X.
on a set X means that every element defines a bijective map on a set in a way compatible with the group structure. When X has more structure, it is useful to restrict this notion further: a representation of G on a vector space
V is a group homomorphism
:
where GL
(V) consists of the invertible linear transformations of V. In other words, to every group element g is assigned an automorphism
ρ(g) such that ρ(g) ∘ ρ(h) = ρ(gh) for any h in G.
This definition can be understood in two directions, both of which give rise to whole new domains of mathematics. On the one hand, it may yield new information about the group G: often, the group operation in G is abstractly given, but via ρ, it corresponds to the multiplication of matrices
, which is very explicit. On the other hand, given a well-understood group acting on a complicated object, this simplifies the study of the object in question.
For example, if G is finite, it is known
that V above decomposes into irreducible parts. These parts in turn are much more easily manageable than the whole V (via Schur's lemma
).
Given a group G, representation theory
then asks what representations of G exist. There are several settings, and the employed methods and obtained results are rather different in every case: representation theory of finite groups
and representations of Lie group
s are two main subdomains of the theory. The totality of representations is governed by the group's characters
. For example, Fourier polynomial
s can be interpreted as the characters of U(1)
, the group of complex numbers of absolute value
1, acting on the L2
-space of periodic functions.
is a mapping of the object onto itself which preserves the structure. This occurs in many cases, for example
The axioms of a group formalize the essential aspects of symmetry
. Symmetries form a group: they are closed
because if you take a symmetry of an object, and then apply another symmetry, the result will still be a symmetry. The identity keeping the object fixed is always a symmetry of an object. Existence of inverses is guaranteed by undoing the symmetry and the associativity comes from the fact that symmetries are functions on a space, and composition of functions are associative.
Frucht's theorem
says that every group is the symmetry group of some graph
. So every abstract group is actually the symmetries of some explicit object.
The saying of "preserving the structure" of an object can be made precise by working in a category
. Maps preserving the structure are then the morphisms, and the symmetry group is the automorphism group of the object in question.
are special cases of groups. Rings
, for example, can be viewed as abelian group
s (corresponding to addition) together with a second operation (corresponding to multiplication). Therefore group theoretic arguments underlie large parts of the theory of those entities.
Galois theory
uses groups to describe the symmetries of the roots of a polynomial (or more precisely the automorphisms of the algebras generated by these roots). The fundamental theorem of Galois theory
provides a link between algebraic field extensions and group theory. It gives an effective criterion for the solvability of polynomial equations in terms of the solvability of the corresponding Galois group
. For example, S5, the symmetric group
in 5 elements, is not solvable which implies that the general quintic equation
cannot be solved by radicals in the way equations of lower degree can. The theory, being one of the historical roots of group theory, is still fruitfully applied to yield new results in areas such as class field theory
.
Algebraic topology
is another domain which prominently associates
groups to the objects the theory is interested in. There, groups are used to describe certain invariants of topological space
s. They are called "invariants" because they are defined in such a way that they do not change if the space is subjected to some deformation
. For example, the fundamental group
"counts" how many paths in the space are essentially different. The Poincaré conjecture
, proved in 2002/2003 by Grigori Perelman
is a prominent application of this idea. The influence is not unidirectional, though. For example, algebraic topology makes use of Eilenberg–MacLane spaces which are spaces with prescribed homotopy groups. Similarly algebraic K-theory
stakes in a crucial way on classifying space
s of groups. Finally, the name of the torsion subgroup
of an infinite group shows the legacy of topology in group theory.

 Algebraic geometry
Algebraic geometry
and cryptography
likewise uses group theory in many ways. Abelian varieties have been introduced above. The presence of the group operation yields additional information which makes these varieties particularly accessible. They also often serve as a test for new conjectures. The one-dimensional case, namely elliptic curve
s is studied in particular detail. They are both theoretically and practically intriguing. Very large groups of prime order constructed in Elliptic-Curve Cryptography
serve for public key cryptography. Cryptographical methods of this kind benefit from the flexibility of the geometric objects, hence their group structures, together with the complicated structure of these groups, which make the discrete logarithm
very hard to calculate. One of the earliest encryption protocols, Caesar's cipher
, may also be interpreted as a (very easy) group operation. In another direction, toric varieties are algebraic varieties
acted on by a torus
. Toroidal embeddings have recently led to advances in algebraic geometry
, in particular resolution of singularities
.
Algebraic number theory
is a special case of group theory, thereby following the rules of the latter. For example, Euler's product formula
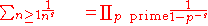
captures the fact
that any integer decomposes in a unique way into primes
. The failure of this statement for more general rings gives rise to class groups and regular primes, which feature in Kummer's
treatment of Fermat's Last Theorem
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, group theory studies the algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s known as groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
.
The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, and vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s can all be seen as groups endowed with additional operation
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
s and axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s. Groups recur throughout mathematics, and the methods of group theory have strongly influenced many parts of algebra. Linear algebraic group
Linear algebraic group
In mathematics, a linear algebraic group is a subgroup of the group of invertible n×n matrices that is defined by polynomial equations...
s and Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s are two branches of group theory that have experienced tremendous advances and have become subject areas in their own right.
Various physical systems, such as crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
s and the hydrogen atom
Hydrogen atom
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively-charged proton and a single negatively-charged electron bound to the nucleus by the Coulomb force...
, can be modelled by symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
s. Thus group theory and the closely related representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
have many applications in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and chemistry
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
.
One of the most important mathematical achievements of the 20th century was the collaborative effort, taking up more than 10,000 journal pages and mostly published between 1960 and 1980, that culminated in a complete classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
.
History
Group theory has three main historical sources: number theoryNumber theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the theory of algebraic equations, and geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
. The number-theoretic strand was begun by Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, and developed by Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
's work on modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
and additive and multiplicative groups related to quadratic field
Quadratic field
In algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q. It is easy to show that the map d ↦ Q is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields...
s. Early results about permutation group
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
s were obtained by Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
, Ruffini
Paolo Ruffini
Paolo Ruffini was an Italian mathematician and philosopher.By 1788 he had earned university degrees in philosophy, medicine/surgery, and mathematics...
, and Abel
Niels Henrik Abel
Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
in their quest for general solutions of polynomial equations of high degree. Évariste Galois
Évariste Galois
Évariste Galois was a French mathematician born in Bourg-la-Reine. While still in his teens, he was able to determine a necessary and sufficient condition for a polynomial to be solvable by radicals, thereby solving a long-standing problem...
coined the term "group" and established a connection, now known as Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
, between the nascent theory of groups and field theory
Field theory (mathematics)
Field theory is a branch of mathematics which studies the properties of fields. A field is a mathematical entity for which addition, subtraction, multiplication and division are well-defined....
. In geometry, groups first became important in projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
and, later, non-Euclidean geometry
Non-Euclidean geometry
Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
. Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
's Erlangen program
Erlangen program
An influential research program and manifesto was published in 1872 by Felix Klein, under the title Vergleichende Betrachtungen über neuere geometrische Forschungen...
proclaimed group theory to be the organizing principle of geometry.
Galois
Évariste Galois
Évariste Galois was a French mathematician born in Bourg-la-Reine. While still in his teens, he was able to determine a necessary and sufficient condition for a polynomial to be solvable by radicals, thereby solving a long-standing problem...
, in the 1830s, was the first to employ groups to determine the solvability of polynomial equations. Arthur Cayley
Arthur Cayley
Arthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....
and Augustin Louis Cauchy
Augustin Louis Cauchy
Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
pushed these investigations further by creating the theory of permutation group
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
. The second historical source for groups stems from geometrical
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
situations. In an attempt to come to grips with possible geometries (such as euclidean
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, hyperbolic
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
or projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
) using group theory, Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
initiated the Erlangen programme. Sophus Lie
Sophus Lie
Marius Sophus Lie was a Norwegian mathematician. He largely created the theory of continuous symmetry, and applied it to the study of geometry and differential equations.- Biography :...
, in 1884, started using groups (now called Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s) attached to analytic problems. Thirdly, groups were (first implicitly and later explicitly) used in algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
.
The different scope of these early sources resulted in different notions of groups. The theory of groups was unified starting around 1880. Since then, the impact of group theory has been ever growing, giving rise to the birth of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
in the early 20th century, representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, and many more influential spin-off domains. The classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
is a vast body of work from the mid 20th century, classifying all the finite simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
s.
Main classes of groups
The range of groups being considered has gradually expanded from finite permutation groupPermutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
s and special examples of matrix group
Matrix group
In mathematics, a matrix group is a group G consisting of invertible matrices over some field K, usually fixed in advance, with operations of matrix multiplication and inversion. More generally, one can consider n × n matrices over a commutative ring R...
s to abstract groups that may be specified through a presentation
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
by generators and relations.
Permutation groups
The first class of groups to undergo a systematic study was permutation groupPermutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
s. Given any set X and a collection G of bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
s of X into itself (known as permutations) that is closed under compositions and inverses, G is a group acting
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on X. If X consists of n elements and G consists of all permutations, G is the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn; in general, any permutation group G is a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of the symmetric group of X. An early construction due to Cayley
Arthur Cayley
Arthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....
exhibited any group as a permutation group, acting on itself (X = G) by means of the left regular representation
Regular representation
In mathematics, and in particular the theory of group representations, the regular representation of a group G is the linear representation afforded by the group action of G on itself by translation....
.
In many cases, the structure of a permutation group can be studied using the properties of its action on the corresponding set. For example, in this way one proves that for n ≥ 5, the alternating group An is simple
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
, i.e. does not admit any proper normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
s. This fact plays a key role in the impossibility of solving a general algebraic equation of degree n ≥ 5 in radicals
Abel–Ruffini theorem
In algebra, the Abel–Ruffini theorem states that there is no general algebraic solution—that is, solution in radicals— to polynomial equations of degree five or higher.- Interpretation :...
.
Matrix groups
The next important class of groups is given by matrix groups, or linear groups. Here G is a set consisting of invertible matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
of given order n over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K that is closed under the products and inverses. Such a group acts on the n-dimensional vector space Kn by linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s. This action makes matrix groups conceptually similar to permutation groups, and the geometry of the action may be usefully exploited to establish properties of the group G.
Transformation groups
Permutation groups and matrix groups are special cases of transformation groups: groups that act on a certain space X preserving its inherent structure. In the case of permutation groups, X is a set; for matrix groups, X is a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. The concept of a transformation group is closely related with the concept of a symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
: transformation groups frequently consist of all transformations that preserve a certain structure.
The theory of transformation groups forms a bridge connecting group theory with differential geometry. A long line of research, originating with Lie
Sophus Lie
Marius Sophus Lie was a Norwegian mathematician. He largely created the theory of continuous symmetry, and applied it to the study of geometry and differential equations.- Biography :...
and Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
, considers group actions on manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s by homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
s or diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s. The groups themselves may be discrete
Discrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
or continuous.
Abstract groups
Most groups considered in the first stage of the development of group theory were "concrete", having been realized through numbers, permutations, or matrices. It was not until the late nineteenth century that the idea of an abstract group as a set with operations satisfying a certain system of axioms began to take hold. A typical way of specifying an abstract group is through a presentationPresentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
by generators and relations,
A significant source of abstract groups is given by the construction of a factor group, or quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
, G/H, of a group G by a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
H. Class groups of algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
s were among the earliest examples of factor groups, of much interest in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
. If a group G is a permutation group on a set X, the factor group G/H is no longer acting on X; but the idea of an abstract group permits one not to worry about this discrepancy.
The change of perspective from concrete to abstract groups makes it natural to consider properties of groups that are independent of a particular realization, or in modern language, invariant under isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
, as well as the classes of group with a given such property: finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s, periodic group
Periodic group
In group theory, a periodic group or a torsion group is a group in which each element has finite order. All finite groups are periodic. The concept of a periodic group should not be confused with that of a cyclic group, although all finite cyclic groups are periodic.The exponent of a periodic group...
s, simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
s, solvable group
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
s, and so on. Rather than exploring properties of an individual group, one seeks to establish results that apply to a whole class of groups. The new paradigm was of paramount importance for the development of mathematics: it foreshadowed the creation of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
in the works of Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
, Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
, Emmy Noether
Emmy Noether
Amalie Emmy Noether was an influential German mathematician known for her groundbreaking contributions to abstract algebra and theoretical physics. Described by David Hilbert, Albert Einstein and others as the most important woman in the history of mathematics, she revolutionized the theories of...
, and mathematicians of their school.
Topological and algebraic groups
An important elaboration of the concept of a group occurs if G is endowed with additional structure, notably, of a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
, or algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
. If the group operations m (multiplication) and i (inversion),
are compatible with this structure, i.e. are continuous, smooth or regular
Regular map (algebraic geometry)
In algebraic geometry, a regular map between affine varieties is a mapping which is given by polynomials. For example, if X and Y are subvarieties of An resp...
(in the sense of algebraic geometry) maps then G becomes a topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
, a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, or an algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
.
The presence of extra structure relates these types of groups with other mathematical disciplines and means that more tools are available in their study. Topological groups form a natural domain for abstract harmonic analysis, whereas Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s (frequently realized as transformation groups) are the mainstays of differential geometry and unitary representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
. Certain classification questions that cannot be solved in general can be approached and resolved for special subclasses of groups. Thus, compact connected Lie groups have been completely classified. There is a fruitful relation between infinite abstract groups and topological groups: whenever a group Γ can be realized as a lattice
Lattice (discrete subgroup)
In Lie theory and related areas of mathematics, a lattice in a locally compact topological group is a discrete subgroup with the property that the quotient space has finite invariant measure...
in a topological group G, the geometry and analysis pertaining to G yield important results about Γ. A comparatively recent trend in the theory of finite groups exploits their connections with compact topological groups (profinite groups): for example, a single p-adic analytic group
Powerful p-group
In mathematics, in the field of group theory, especially in the study of p-groups and pro-p-groups, the concept of powerful p-groups plays an important role. They were introduced in , where a number of applications are given, including results on Schur multipliers...
G has a family of quotients which are finite p-groups
P-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
of various orders, and properties of G translate into the properties of its finite quotients.
Combinatorial and geometric group theory
Groups can be described in different ways. Finite groups can be described by writing down the group table consisting of all possible multiplications . A more important way of defining a group is by generators and relations, also called the presentation of a group. Given any set F of generators {gi}i ∈ I, the free groupFree group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
generated by F surjects onto the group G. The kernel of this map is called subgroup of relations, generated by some subset D. The presentation is usually denoted by 〈F | D 〉. For example, the group Z = 〈a | 〉 can be generated by one element a (equal to +1 or −1) and no relations, because n·1 never equals 0 unless n is zero. A string consisting of generator symbols and their inverses is called a word.
Combinatorial group theory
Combinatorial group theory
In mathematics, combinatorial group theory is the theory of free groups, and the concept of a presentation of a group by generators and relations...
studies groups from the perspective of generators and relations. It is particularly useful where finiteness assumptions are satisfied, for example finitely generated groups, or finitely presented groups (i.e. in addition the relations are finite). The area makes use of the connection of graphs
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
via their fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
s. For example, one can show that every subgroup of a free group is free.
There are several natural questions arising from giving a group by its presentation. The word problem
Word problem for groups
In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
asks whether two words are effectively the same group element. By relating the problem to Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
s, one can show that there is in general no algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
solving this task. An equally difficult problem is, whether two groups given by different presentations are actually isomorphic. For example Z can also be presented by
- 〈x, y | xyxyx = 1⟩
and it is not obvious (but true) that this presentation is isomorphic to the standard one above.

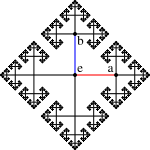
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
attacks these problems from a geometric viewpoint, either by viewing groups as geometric objects, or by finding suitable geometric objects a group acts on. The first idea is made precise by means of the Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
, whose vertices correspond to group elements and edges correspond to right multiplication in the group. Given two elements, one constructs the word metric given by the length of the minimal path between the elements. A theorem of Milnor
John Milnor
John Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...
and Svarc then says that given a group G acting in a reasonable manner on a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
X, for example a compact manifold, then G is quasi-isometric
Quasi-isometry
In mathematics, a quasi-isometry is a means to compare the large-scale structure of metric spaces. The concept is especially important in Gromov's geometric group theory.-Definition:...
(i.e. looks similar from the far) to the space X.
Representation of groups
Saying that a group G actsGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on a set X means that every element defines a bijective map on a set in a way compatible with the group structure. When X has more structure, it is useful to restrict this notion further: a representation of G on a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V is a group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
:
- ρ : G → GL(V),
where GL
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
(V) consists of the invertible linear transformations of V. In other words, to every group element g is assigned an automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
ρ(g) such that ρ(g) ∘ ρ(h) = ρ(gh) for any h in G.
This definition can be understood in two directions, both of which give rise to whole new domains of mathematics. On the one hand, it may yield new information about the group G: often, the group operation in G is abstractly given, but via ρ, it corresponds to the multiplication of matrices
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
, which is very explicit. On the other hand, given a well-understood group acting on a complicated object, this simplifies the study of the object in question.
For example, if G is finite, it is known
Maschke's theorem
In mathematics, Maschke's theorem, named after Heinrich Maschke, is a theorem in group representation theory that concerns the decomposition of representations of a finite group into irreducible pieces...
that V above decomposes into irreducible parts. These parts in turn are much more easily manageable than the whole V (via Schur's lemma
Schur's lemma
In mathematics, Schur's lemma is an elementary but extremely useful statement in representation theory of groups and algebras. In the group case it says that if M and N are two finite-dimensional irreducible representations...
).
Given a group G, representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
then asks what representations of G exist. There are several settings, and the employed methods and obtained results are rather different in every case: representation theory of finite groups
Representation theory of finite groups
In mathematics, representation theory is a technique for analyzing abstract groups in terms of groups of linear transformations. See the article on group representations for an introduction...
and representations of Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s are two main subdomains of the theory. The totality of representations is governed by the group's characters
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
. For example, Fourier polynomial
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
s can be interpreted as the characters of U(1)
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
, the group of complex numbers of absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
1, acting on the L2
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
-space of periodic functions.
Connection of groups and symmetry
Given a structured object X of any sort, a symmetrySymmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
is a mapping of the object onto itself which preserves the structure. This occurs in many cases, for example
- If X is a set with no additional structure, a symmetry is a bijectiveBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
map from the set to itself, giving rise to permutation groupPermutation groupIn mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
s. - If the object X is a set of points in the plane with its metricMetric (mathematics)In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
structure or any other metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, a symmetry is a bijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
of the set to itself which preserves the distance between each pair of points (an isometryIsometryIn mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
). The corresponding group is called isometry groupIsometry groupIn mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...
of X. - If instead angleAngleIn geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s are preserved, one speaks of conformal mapConformal mapIn mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
s. Conformal maps give rise to Kleinian groupKleinian groupIn mathematics, a Kleinian group is a discrete subgroup of PSL. The group PSL of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic...
s, for example. - Symmetries are not restricted to geometrical objects, but include algebraic objects as well. For instance, the equation
-
- has the two solutions
 , and
, and  . In this case, the group that exchanges the two roots is the Galois groupGalois groupIn mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
. In this case, the group that exchanges the two roots is the Galois groupGalois groupIn mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
belonging to the equation. Every polynomial equation in one variable has a Galois group, that is a certain permutation group on its roots.
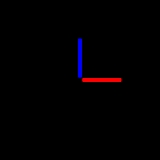
The axioms of a group formalize the essential aspects of symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
. Symmetries form a group: they are closed
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
because if you take a symmetry of an object, and then apply another symmetry, the result will still be a symmetry. The identity keeping the object fixed is always a symmetry of an object. Existence of inverses is guaranteed by undoing the symmetry and the associativity comes from the fact that symmetries are functions on a space, and composition of functions are associative.
Frucht's theorem
Frucht's theorem
Frucht's theorem is a theorem in algebraic graph theory conjectured by Dénes Kőnig in 1936 and proved by Robert Frucht in 1939. It states that every finite group is the group of symmetries of a finite undirected graph...
says that every group is the symmetry group of some graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
. So every abstract group is actually the symmetries of some explicit object.
The saying of "preserving the structure" of an object can be made precise by working in a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
. Maps preserving the structure are then the morphisms, and the symmetry group is the automorphism group of the object in question.
Applications of group theory
Applications of group theory abound. Almost all structures in abstract algebraAbstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
are special cases of groups. Rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, for example, can be viewed as abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s (corresponding to addition) together with a second operation (corresponding to multiplication). Therefore group theoretic arguments underlie large parts of the theory of those entities.
Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
uses groups to describe the symmetries of the roots of a polynomial (or more precisely the automorphisms of the algebras generated by these roots). The fundamental theorem of Galois theory
Fundamental theorem of Galois theory
In mathematics, the fundamental theorem of Galois theory is a result that describes the structure of certain types of field extensions.In its most basic form, the theorem asserts that given a field extension E /F which is finite and Galois, there is a one-to-one correspondence between its...
provides a link between algebraic field extensions and group theory. It gives an effective criterion for the solvability of polynomial equations in terms of the solvability of the corresponding Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
. For example, S5, the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
in 5 elements, is not solvable which implies that the general quintic equation
Quintic equation
In mathematics, a quintic function is a function of the formg=ax^5+bx^4+cx^3+dx^2+ex+f,\,where a, b, c, d, e and f are members of a field, typically the rational numbers, the real numbers or the complex numbers, and a is nonzero...
cannot be solved by radicals in the way equations of lower degree can. The theory, being one of the historical roots of group theory, is still fruitfully applied to yield new results in areas such as class field theory
Class field theory
In mathematics, class field theory is a major branch of algebraic number theory that studies abelian extensions of number fields.Most of the central results in this area were proved in the period between 1900 and 1950...
.
Algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
is another domain which prominently associates
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
groups to the objects the theory is interested in. There, groups are used to describe certain invariants of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s. They are called "invariants" because they are defined in such a way that they do not change if the space is subjected to some deformation
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
. For example, the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
"counts" how many paths in the space are essentially different. The Poincaré conjecture
Poincaré conjecture
In mathematics, the Poincaré conjecture is a theorem about the characterization of the three-dimensional sphere , which is the hypersphere that bounds the unit ball in four-dimensional space...
, proved in 2002/2003 by Grigori Perelman
Grigori Perelman
Grigori Yakovlevich Perelman is a Russian mathematician who has made landmark contributions to Riemannian geometry and geometric topology.In 1992, Perelman proved the soul conjecture. In 2002, he proved Thurston's geometrization conjecture...
is a prominent application of this idea. The influence is not unidirectional, though. For example, algebraic topology makes use of Eilenberg–MacLane spaces which are spaces with prescribed homotopy groups. Similarly algebraic K-theory
Algebraic K-theory
In mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
stakes in a crucial way on classifying space
Classifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
s of groups. Finally, the name of the torsion subgroup
Torsion subgroup
In the theory of abelian groups, the torsion subgroup AT of an abelian group A is the subgroup of A consisting of all elements that have finite order...
of an infinite group shows the legacy of topology in group theory.


Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
and cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
likewise uses group theory in many ways. Abelian varieties have been introduced above. The presence of the group operation yields additional information which makes these varieties particularly accessible. They also often serve as a test for new conjectures. The one-dimensional case, namely elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s is studied in particular detail. They are both theoretically and practically intriguing. Very large groups of prime order constructed in Elliptic-Curve Cryptography
Elliptic curve cryptography
Elliptic curve cryptography is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields. The use of elliptic curves in cryptography was suggested independently by Neal Koblitz and Victor S...
serve for public key cryptography. Cryptographical methods of this kind benefit from the flexibility of the geometric objects, hence their group structures, together with the complicated structure of these groups, which make the discrete logarithm
Discrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
very hard to calculate. One of the earliest encryption protocols, Caesar's cipher
Caesar cipher
In cryptography, a Caesar cipher, also known as a Caesar's cipher, the shift cipher, Caesar's code or Caesar shift, is one of the simplest and most widely known encryption techniques. It is a type of substitution cipher in which each letter in the plaintext is replaced by a letter some fixed number...
, may also be interpreted as a (very easy) group operation. In another direction, toric varieties are algebraic varieties
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
acted on by a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
. Toroidal embeddings have recently led to advances in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, in particular resolution of singularities
Resolution of singularities
In algebraic geometry, the problem of resolution of singularities asks whether every algebraic variety V has a resolution, a non-singular variety W with a proper birational map W→V...
.
Algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
is a special case of group theory, thereby following the rules of the latter. For example, Euler's product formula
Euler product
In number theory, an Euler product is an expansion of a Dirichlet series into an infinite product indexed by prime numbers. The name arose from the case of the Riemann zeta-function, where such a product representation was proved by Leonhard Euler.-Definition:...
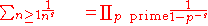
captures the fact
Fundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
that any integer decomposes in a unique way into primes
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. The failure of this statement for more general rings gives rise to class groups and regular primes, which feature in Kummer's
Ernst Kummer
Ernst Eduard Kummer was a German mathematician. Skilled in applied mathematics, Kummer trained German army officers in ballistics; afterwards, he taught for 10 years in a gymnasium, the German equivalent of high school, where he inspired the mathematical career of Leopold Kronecker.-Life:Kummer...
treatment of Fermat's Last Theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
.
- The concept of the Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
(named after mathematician Sophus LieSophus LieMarius Sophus Lie was a Norwegian mathematician. He largely created the theory of continuous symmetry, and applied it to the study of geometry and differential equations.- Biography :...
) is important in the study of differential equations and manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s; they describe the symmetries of continuous geometric and analytical structures. Analysis on these and other groups is called harmonic analysisHarmonic analysisHarmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
. Haar measureHaar measureIn mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
s, that is integrals invariant under the translation in a Lie group, are used for pattern recognitionPattern recognitionIn machine learning, pattern recognition is the assignment of some sort of output value to a given input value , according to some specific algorithm. An example of pattern recognition is classification, which attempts to assign each input value to one of a given set of classes...
and other image processingImage processingIn electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
techniques.
- In combinatoricsCombinatoricsCombinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, the notion of permutationPermutationIn mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
group and the concept of group action are often used to simplify the counting of a set of objects; see in particular Burnside's lemmaBurnside's lemmaBurnside's lemma, sometimes also called Burnside's counting theorem, the Cauchy-Frobenius lemma or the orbit-counting theorem, is a result in group theory which is often useful in taking account of symmetry when counting mathematical objects. Its various eponyms include William Burnside, George...
.

- The presence of the 12-periodicityPeriodic groupIn group theory, a periodic group or a torsion group is a group in which each element has finite order. All finite groups are periodic. The concept of a periodic group should not be confused with that of a cyclic group, although all finite cyclic groups are periodic.The exponent of a periodic group...
in the circle of fifthsCircle of fifthsIn music theory, the circle of fifths shows the relationships among the 12 tones of the chromatic scale, their corresponding key signatures, and the associated major and minor keys...
yields applications of elementary group theory in musical set theory.
- In physicsPhysicsPhysics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, groups are important because they describe the symmetries which the laws of physics seem to obey. According to Noether's theoremNoether's theoremNoether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
, every symmetry of a physical system corresponds to a conservation lawConservation lawIn physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
of the system. Physicists are very interested in group representations, especially of Lie groups, since these representations often point the way to the "possible" physical theories. Examples of the use of groups in physics include the Standard ModelStandard ModelThe Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
, gauge theoryGauge theoryIn physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
, the Lorentz groupLorentz groupIn physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
, and the Poincaré groupPoincaré groupIn physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
.
- In chemistryChemistryChemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
and materials scienceMaterials scienceMaterials science is an interdisciplinary field applying the properties of matter to various areas of science and engineering. This scientific field investigates the relationship between the structure of materials at atomic or molecular scales and their macroscopic properties. It incorporates...
, groups are used to classify crystal structureCrystal structureIn mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
s, regular polyhedra, and the symmetries of moleculesMolecular symmetryMolecular symmetry in chemistry describes the symmetry present in molecules and the classification of molecules according to their symmetry. Molecular symmetry is a fundamental concept in chemistry, as it can predict or explain many of a molecule's chemical properties, such as its dipole moment...
. The assigned point groups can then be used to determine physical properties (such as polarity and chiralityChirality (chemistry)A chiral molecule is a type of molecule that lacks an internal plane of symmetry and thus has a non-superimposable mirror image. The feature that is most often the cause of chirality in molecules is the presence of an asymmetric carbon atom....
), spectroscopic properties (particularly useful for Raman spectroscopyRaman spectroscopyRaman spectroscopy is a spectroscopic technique used to study vibrational, rotational, and other low-frequency modes in a system.It relies on inelastic scattering, or Raman scattering, of monochromatic light, usually from a laser in the visible, near infrared, or near ultraviolet range...
and infrared spectroscopyInfrared spectroscopyInfrared spectroscopy is the spectroscopy that deals with the infrared region of the electromagnetic spectrum, that is light with a longer wavelength and lower frequency than visible light. It covers a range of techniques, mostly based on absorption spectroscopy. As with all spectroscopic...
), and to construct molecular orbitalMolecular orbitalIn chemistry, a molecular orbital is a mathematical function describing the wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The term "orbital" was first...
s.
See also
- Group (mathematics)Group (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
- Glossary of group theoryGlossary of group theoryA group is a set G closed under a binary operation • satisfying the following 3 axioms:* Associativity: For all a, b and c in G, • c = a • ....
- List of group theory topics
External links
- History of the abstract group concept
- Higher dimensional group theory This presents a view of group theory as level one of a theory which extends in all dimensions, and has applications in homotopy theory and to higher dimensional nonabelian methods for local-to-global problems.
- Plus teacher and student package: Group Theory This package brings together all the articles on group theory from Plus, the online mathematics magazine produced by the Millennium Mathematics Project at the University of Cambridge, exploring applications and recent breakthroughs, and giving explicit definitions and examples of groups.
- US Naval Academy group theory guide A general introduction to group theory with exercises written by Tony Gaglione.