
Division (mathematics)
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in elementary arithmetic
Elementary arithmetic
Elementary arithmetic is the simplified portion of arithmetic which is considered necessary and appropriate during primary education. It includes the operations of addition, subtraction, multiplication, and division. It is taught in elementary school....
, division (÷) is an arithmetic operation.
Specifically, if c times b equals a, written:

where b is not zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
, then a divided by b equals c, written:
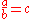
For instance,
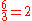
since
 .
.In the above expression, a is called the dividend, b the divisor and c the quotient
Quotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
.
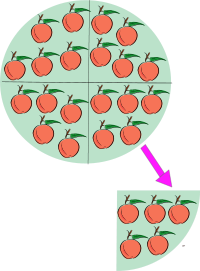
Conceptually, division describes two distinct but related settings. Partitioning involves taking a set of size a and forming b groups that are equal in size. The size of each group formed, c, is the quotient of a and b. Quotative division involves taking a set of size a and forming groups of size b. The number of groups of this size that can be formed, c, is the quotient of a and b.
Teaching division usually leads to the concept of fraction
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
s being introduced to students. Unlike addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
, and multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
, the set of all integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s is not closed
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
under division. Dividing two integers may result in a remainder
Remainder
In arithmetic, the remainder is the amount "left over" after the division of two integers which cannot be expressed with an integer quotient....
. To complete the division of the remainder, the number system
Number system
In mathematics, a 'number system' is a set of numbers, , together with one or more operations, such as addition or multiplication....
is extended to include fractions or rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s as they are more generally called.
Notation
Division is often shown in algebra and science by placing the dividend over the divisor with a horizontal line, also called a vinculum or fraction barFraction
In common usage a fraction is any part of a unit.Fraction may also mean:*Fraction , one of more equal parts of something, eg...
, between them. For example, a divided by b is written
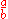
This can be read out loud as "a divided by b", "a by b" or "a over b". A way to express division all on one line is to write the dividend, or numerator then a slash
Slash (punctuation)
The slash is a sign used as a punctuation mark and for various other purposes. It is now often called a forward slash , and many other alternative names.-History:...
, then the divisor, or denominator like this:
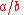
This is the usual way to specify division in most computer programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s since it can easily be typed as a simple sequence of ASCII
ASCII
The American Standard Code for Information Interchange is a character-encoding scheme based on the ordering of the English alphabet. ASCII codes represent text in computers, communications equipment, and other devices that use text...
characters.
A typographical variation, which is halfway between these two forms, uses a solidus
Solidus (punctuation)
The solidus is a punctuation mark used to indicate fractions including fractional currency. It may also be called a shilling mark, an in-line fraction bar, or a fraction slash....
(fraction slash) but elevates the dividend, and lowers the divisor:
Any of these forms can be used to display a fraction
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
. A fraction is a division expression where both dividend and divisor are integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s (although typically called the numerator and denominator), and there is no implication that the division needs to be evaluated further. A second way to show division is to use the obelus
Obelus
An obelus is a symbol consisting of a short horizontal line with a dot above and below. It is mainly used to represent the mathematical operation of division. It is therefore commonly referred to as the division sign.- History :The word "obelus" comes from the Greek word for a sharpened stick,...
(or division sign), common in arithmetic, in this manner:

This form is infrequent except in elementary arithmetic. The obelus is also used alone to represent the division operation itself, as for instance as a label on a key of a calculator
Calculator
An electronic calculator is a small, portable, usually inexpensive electronic device used to perform the basic operations of arithmetic. Modern calculators are more portable than most computers, though most PDAs are comparable in size to handheld calculators.The first solid-state electronic...
.
In some non-English
English language
English is a West Germanic language that arose in the Anglo-Saxon kingdoms of England and spread into what was to become south-east Scotland under the influence of the Anglian medieval kingdom of Northumbria...
-speaking cultures, "a divided by b" is written a : b. However, in English usage the colon
Colon (punctuation)
The colon is a punctuation mark consisting of two equally sized dots centered on the same vertical line.-Usage:A colon informs the reader that what follows the mark proves, explains, or lists elements of what preceded the mark....
is restricted to expressing the related concept of ratio
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
s (then "a is to b").
In elementary mathematics the notation
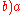 or
or 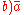 is used to denote a divided by b. This notation was first introduced by Michael Stifel
is used to denote a divided by b. This notation was first introduced by Michael StifelMichael Stifel
Michael Stifel or Styfel was a German monk and mathematician. He was an Augustinian who became an early supporter of Martin Luther. Stifel was later appointed professor of mathematics at Jena University...
in Arithmetica integra, published in 1544.
Computing division
Division is often introduced through the notion of "sharing out" a set of objects, for example a pile of sweets, into a number of equal portions. Distributing the objects several at a time in each round of sharing to each portion leads to the idea of "chunkingChunking (division)
In mathematics education at primary school level, chunking is an elementary approach for solving simple division questions, by repeated subtraction....
", i.e. division by repeated subtraction.
More systematic and more efficient (but also more formalised and more rule-based, and more removed from an overall holistic picture of what division is achieving), a person who knows the multiplication tables can divide two integers using pencil and paper and the method of short division
Short division
In arithmetic, short division is a procedure which breaks down a division problem into a series of easy steps. As in all division problems, one number, called the dividend, is divided by another, called the divisor, producing a result called the quotient. Short division is an abbreviated form of...
, if the divisor is simple, or long division
Long division
In arithmetic, long division is a standard procedure suitable for dividing simple or complex multidigit numbers. It breaks down a division problem into a series of easier steps. As in all division problems, one number, called the dividend, is divided by another, called the divisor, producing a...
for larger integer divisors. If the dividend has a fractional
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
part (expressed as a decimal fraction), we can continue the algorithm past the ones place as far as desired. If the divisor has a fractional part, we can restate the problem by moving the decimal to the right in both numbers until the divisor has no fraction.
Modern computers compute division by methods that are faster than long division: see Division (digital)
Division (digital)
Several algorithms exist to perform division in digital designs. These algorithms fall into two main categories: slow division and fast division. Slow division algorithms produce one digit of the final quotient per iteration. Examples of slow division include restoring, non-performing restoring,...
.
A person can calculate division with an abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
by repeatedly placing the dividend on the abacus, and then subtracting the divisor the offset of each digit in the result, counting the number of divisions possible at each offset.
A person can use logarithm tables to divide two numbers, by subtracting the two numbers' logarithms, then looking up the antilogarithm of the result.
A person can calculate division with a slide rule
Slide rule
The slide rule, also known colloquially as a slipstick, is a mechanical analog computer. The slide rule is used primarily for multiplication and division, and also for functions such as roots, logarithms and trigonometry, but is not normally used for addition or subtraction.Slide rules come in a...
by aligning the divisor on the C scale with the dividend on the D scale. The quotient can be found on the D scale where it is aligned with the left index on the C scale. The user is responsible, however, for mentally keeping track of the decimal point.
In modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
, some numbers have a multiplicative inverse with respect to the modulus. We can calculate division by multiplication in such a case. This approach is useful in computers that do not have a fast division instruction.
Division algorithm
The division algorithmDivision algorithm
In mathematics, and more particularly in arithmetic, the usual process of division of integers producing a quotient and a remainder can be specified precisely by a theorem stating that these exist uniquely with given properties. An integer division algorithm is any effective method for producing...
is a mathematical theorem that precisely expresses the outcome of the usual process of division of integers. In particular, the theorem asserts that integers called the quotient q and remainder r always exist and that they are uniquely determined by the dividend a and divisor d, with d ≠ 0. Formally, the theorem is stated as follows: There exist unique
Uniqueness quantification
In mathematics and logic, the phrase "there is one and only one" is used to indicate that exactly one object with a certain property exists. In mathematical logic, this sort of quantification is known as uniqueness quantification or unique existential quantification.Uniqueness quantification is...
integers q and r such that a = qd + r and 0 ≤ r < | d |, where | d | denotes the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of d.
Division of integers
Division of integers is not closedClosure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
. Apart from division by zero being undefined, the quotient will not be an integer unless the dividend is an integer multiple of the divisor; for example 26 cannot be divided by 10 to give an integer. In such a case there are four possible approaches.
- Say that 26 cannot be divided by 10; division becomes a partial functionPartial functionIn mathematics, a partial function from X to Y is a function ƒ: X' → Y, where X' is a subset of X. It generalizes the concept of a function by not forcing f to map every element of X to an element of Y . If X' = X, then ƒ is called a total function and is equivalent to a function...
. - Give the answer as a decimal fraction or a mixed number, so
 or
or  This is the approach usually taken in mathematics.
This is the approach usually taken in mathematics. - Give the answer as an integer quotientQuotientIn mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
and a remainderRemainderIn arithmetic, the remainder is the amount "left over" after the division of two integers which cannot be expressed with an integer quotient....
, so
- Give the integer quotient as the answer, so
 This is sometimes called integer division.
This is sometimes called integer division.
One has to be careful when performing division of integers in a computer program
Computer program
A computer program is a sequence of instructions written to perform a specified task with a computer. A computer requires programs to function, typically executing the program's instructions in a central processor. The program has an executable form that the computer can use directly to execute...
. Some programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s, such as C
C (programming language)
C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
, will treat division of integers as in case 4 above, so the answer will be an integer. Other languages, such as MATLAB
MATLAB
MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
, will first convert the integers to real numbers, and then give a real number as the answer, as in case 2 above.
Names and symbols used for integer division include div, /, \, and %. Definitions vary regarding integer division when the quotient is negative: rounding may be toward zero or toward −∞
Extended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
.
Divisibility rule
Divisibility rule
A divisibility rule is a shorthand way of discovering whether a given number is divisible by a fixed divisor without performing the division, usually by examining its digits...
s can sometimes be used to quickly determine whether one integer divides exactly into another.
Division of rational numbers
The result of dividing two rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s is another rational number when the divisor is not 0. We may define division of two rational numbers p/q and r/s by
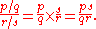
All four quantities are integers, and only p may be 0. This definition ensures that division is the inverse operation of multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
.
Division of real numbers
Division of two real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s results in another real number when the divisor is not 0. It is defined such a/b = c if and only if a = cb and b ≠ 0.
Division by zero
Division of any number by zero (where the divisor is zero) is not defined. This is because zero multiplied by any finite number will always result in a productMultiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
of zero. Entry of such an expression into most calculator
Calculator
An electronic calculator is a small, portable, usually inexpensive electronic device used to perform the basic operations of arithmetic. Modern calculators are more portable than most computers, though most PDAs are comparable in size to handheld calculators.The first solid-state electronic...
s will result in an error message being issued.
Division of complex numbers
Dividing two complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s results in another complex number when the divisor is not 0, defined thus:

All four quantities are real numbers. r and s may not both be 0.
Division for complex numbers expressed in polar form is simpler than the definition above:

Again all four quantities are real numbers. r may not be 0.
Division of polynomials
One can define the division operation for polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s. Then, as in the case of integers, one has a remainder. See polynomial long division
Polynomial long division
In algebra, polynomial long division is an algorithm for dividing a polynomial by another polynomial of the same or lower degree, a generalised version of the familiar arithmetic technique called long division...
or synthetic division
Synthetic division
Synthetic division is a method of performing polynomial long division, with less writing and fewer calculations. It is mostly taught for division by binomials of the formx - a,\ but the method generalizes to division by any monic polynomial...
.
Division of matrices
One can define a division operation for matrices. The usual way to do this is to define , where denotes the inverse of B, but it is far more common to write out explicitly to avoid confusion.Left and right division
Because matrix multiplicationMatrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
is not commutative, one can also define a left division or so-called backslash-division as . For this to be well defined, need not exist, however does need to exist. To avoid confusion, division as defined by is sometimes called right division or slash-division in this context.
Note that with left and right division defined this way, is in general not the same as and nor is the same as , but and .
Matrix division and pseudoinverse
To avoid problems when and/or do not exist, division can also be defined as multiplication with the pseudoinverse, i.e., and , where and denote the pseudoinverse of A and B.Division in abstract algebra
In abstract algebraAbstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
s such as matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
algebras and quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
algebras, fractions such as
 are typically defined as
are typically defined as 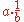 or
or 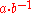 where
where  is presumed to be an invertible element (i.e. there exists a multiplicative inverse
is presumed to be an invertible element (i.e. there exists a multiplicative inverseMultiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
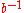 such that
such that 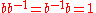 where
where 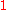 is the multiplicative identity). In an integral domain where such elements may not exist, division can still be performed on equations of the form
is the multiplicative identity). In an integral domain where such elements may not exist, division can still be performed on equations of the form  or
or  by left or right cancellation, respectively. More generally "division" in the sense of "cancellation" can be done in any ring
by left or right cancellation, respectively. More generally "division" in the sense of "cancellation" can be done in any ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
with the aforementioned cancellation properties. If such a ring is finite, then by an application of the pigeonhole principle, every nonzero element of the ring is invertible, so division by any nonzero element is possible in such a ring. To learn about when algebras (in the technical sense) have a division operation, refer to the page on division algebra
Division algebra
In the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field, in which division is possible.- Definitions :...
s. In particular Bott periodicity can be used to show that any real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
normed division algebra
Normed division algebra
In mathematics, a normed division algebra A is a division algebra over the real or complex numbers which is also a normed vector space, with norm || · || satisfying the following property:\|xy\| = \|x\| \|y\| for all x and y in A....
must be isomorphic to either the real numbers R, the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s C, the quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s H, or the octonion
Octonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s O.
Division and calculus
The derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the quotient of two functions is given by the quotient rule:
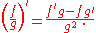
There is no general method to integrate
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
the quotient of two functions.
See also
- 400AD Sunzi division algorithm
- Galley divisionGalley divisionIn arithmetic, the galley method, also known as the batello or the scratch method, was the most widely used method of division in use prior to 1600. The names galea and batello refer to a boat which the outline of the work was thought to resemble.An earlier version of this method was used as early...
- Division by twoDivision by twoIn mathematics, division by two or halving has also been called mediation or dimidiation. The treatment of this as a different operation from multiplication and division by other numbers goes back to the ancient Egyptians, whose multiplication algorithm used division by two as one of its...
- FieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
- GroupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
- Inverse elementInverse elementIn abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
- Order of operationsOrder of operationsIn mathematics and computer programming, the order of operations is a rule used to clarify unambiguously which procedures should be performed first in a given mathematical expression....
- QuasigroupQuasigroupIn mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...
(left division) - Repeating decimalRepeating decimalIn arithmetic, a decimal representation of a real number is called a repeating decimal if at some point it becomes periodic, that is, if there is some finite sequence of digits that is repeated indefinitely...

