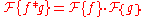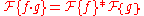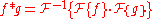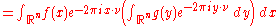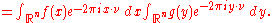Convolution theorem
Encyclopedia
In mathematics
, the convolution theorem states that under suitable
conditions the Fourier transform
of a convolution
is the pointwise product
of Fourier transforms. In other words, convolution in one domain (e.g., time domain
) equals point-wise multiplication in the other domain (e.g., frequency domain
). Versions of the convolution theorem are true for various Fourier-related transforms.
Let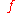
and 
be two function
s with convolution
. (Note that the asterisk
denotes convolution in this context, and not multiplication. The tensor product
symbol
is sometimes used instead.)
Let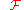
denote the Fourier transform operator, so 
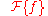and 
are the Fourier transforms of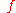 
and 
, respectively.
Then
where
denotes point-wise multiplication. It also works the other way around:
By applying the inverse Fourier transform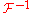
, we can write:
Note that the relationships above are only valid for the form of the Fourier transform shown in the Proof section below. The transform may be normalised in other ways, in which case constant scaling factors (typically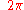
or 
) will appear in the relationships above.
This theorem also holds for the Laplace transform, the two-sided Laplace transform
and, when suitably modified, for the Mellin transform
and Hartley transform
(see Mellin inversion theorem
). It can be extended to the Fourier transform of abstract harmonic analysis defined over locally compact abelian groups.
This formulation is especially useful for implementing a numerical convolution on a computer
: The standard convolution algorithm has quadratic
computational complexity
. With the help of the convolution theorem and the fast Fourier transform
, the complexity of the convolution can be reduced to O(n log n). This can be exploited to construct fast multiplication algorithm
s.
Let f, g belong to L1(Rn). Let
be the Fourier transform of 
and 
be the Fourier transform of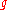 
:
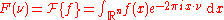
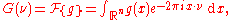
where the dot between x and ν indicates the inner product of Rn.
Let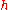
be the convolution
of
and 
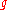
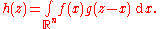
Now notice that
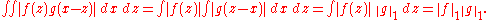
Hence by Fubini's theorem
we have that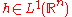
so its Fourier transform 
is defined by the integral formula
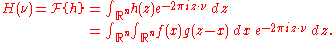
Observe that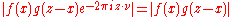
and hence by the argument above we may apply Fubini's theorem again:
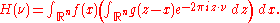
Substitute
; then 
, so:
These two integrals are the definitions of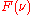
and 
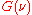, so: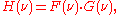
QED
.
The proof is trivial in linear algebra
where convolution is represented by an infinite-dimensional Toeplitz matrix, h, which are known to have the Fourier eigenbasis, F. This means that h can be represented by a diagonal one
, H = (F h F-1),
or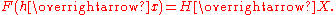
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the convolution theorem states that under suitable
conditions the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of a convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
is the pointwise product
Pointwise product
The pointwise product of two functions is another function, obtained by multiplying the image of the two functions at each value in the domain...
of Fourier transforms. In other words, convolution in one domain (e.g., time domain
Time domain
Time domain is a term used to describe the analysis of mathematical functions, physical signals or time series of economic or environmental data, with respect to time. In the time domain, the signal or function's value is known for all real numbers, for the case of continuous time, or at various...
) equals point-wise multiplication in the other domain (e.g., frequency domain
Frequency domain
In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
). Versions of the convolution theorem are true for various Fourier-related transforms.
Let
and be two functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s with convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
. (Note that the asteriskAsterisk
An asterisk is a typographical symbol or glyph. It is so called because it resembles a conventional image of a star. Computer scientists and mathematicians often pronounce it as star...
denotes convolution in this context, and not multiplication. The tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
symbol
is sometimes used instead.)Let
denote the Fourier transform operator, so 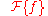and are the Fourier transforms of 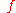and , respectively.Then
where
denotes point-wise multiplication. It also works the other way around:
By applying the inverse Fourier transform
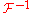, we can write:
Note that the relationships above are only valid for the form of the Fourier transform shown in the Proof section below. The transform may be normalised in other ways, in which case constant scaling factors (typically
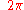or ) will appear in the relationships above.This theorem also holds for the Laplace transform, the two-sided Laplace transform
Two-sided Laplace transform
In mathematics, the two-sided Laplace transform or bilateral Laplace transform is an integral transform closely related to the Fourier transform, the Mellin transform, and the ordinary or one-sided Laplace transform...
and, when suitably modified, for the Mellin transform
Mellin transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...
and Hartley transform
Hartley transform
In mathematics, the Hartley transform is an integral transform closely related to the Fourier transform, but which transforms real-valued functions to real-valued functions. It was proposed as an alternative to the Fourier transform by R. V. L. Hartley in 1942, and is one of many known...
(see Mellin inversion theorem
Mellin inversion theorem
In mathematics, the Mellin inversion formula tells us conditions underwhich the inverse Mellin transform, or equivalently the inverse two-sided Laplace transform, are defined and recover the transformed function....
). It can be extended to the Fourier transform of abstract harmonic analysis defined over locally compact abelian groups.
This formulation is especially useful for implementing a numerical convolution on a computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
: The standard convolution algorithm has quadratic
Quadratic function
A quadratic function, in mathematics, is a polynomial function of the formf=ax^2+bx+c,\quad a \ne 0.The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y-axis....
computational complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
. With the help of the convolution theorem and the fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
, the complexity of the convolution can be reduced to O(n log n). This can be exploited to construct fast multiplication algorithm
Multiplication algorithm
A multiplication algorithm is an algorithm to multiply two numbers. Depending on the size of the numbers, different algorithms are in use...
s.
Proof
The proof here is shown for a particular normalisation of the Fourier transform. As mentioned above, if the transform is normalised differently, then constant scaling factors will appear in the derivation.Let f, g belong to L1(Rn). Let
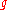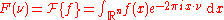
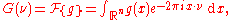
be the Fourier transform of and be the Fourier transform of :where the dot between x and ν indicates the inner product of Rn.
Let
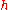be the convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of
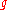
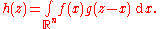
and Now notice that
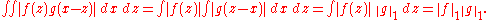
Hence by Fubini's theorem
Fubini's theorem
In mathematical analysis Fubini's theorem, named after Guido Fubini, is a result which gives conditions under which it is possible to compute a double integral using iterated integrals. As a consequence it allows the order of integration to be changed in iterated integrals.-Theorem...
we have that
so its Fourier transform is defined by the integral formula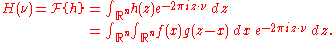Observe that
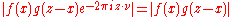and hence by the argument above we may apply Fubini's theorem again: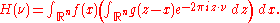Substitute
; then , so:
These two integrals are the definitions of
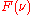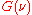and , so: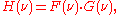QED
Q.E.D.
Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...
.
The proof is trivial in linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
where convolution is represented by an infinite-dimensional Toeplitz matrix, h, which are known to have the Fourier eigenbasis, F. This means that h can be represented by a diagonal one
Eigendecomposition of a matrix
In the mathematical discipline of linear algebra, eigendecomposition or sometimes spectral decomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors...
, H = (F h F-1),
or
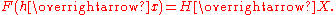
Additional resources
- For visual representation of the use of the convolution theorem in signal processingSignal processingSignal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, see Johns Hopkins UniversityJohns Hopkins UniversityThe Johns Hopkins University, commonly referred to as Johns Hopkins, JHU, or simply Hopkins, is a private research university based in Baltimore, Maryland, United States...
's Java-aided simulation: http://www.jhu.edu/signals/convolve/index.html