
Vector (mathematics and physics)
Encyclopedia
In mathematics and physics, a vector is an element of a vector space
. If n is a non negative integer
and K is either the field
of the real number
s or the field of the complex number
, then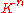 is naturally endowed with a structure of vector space, where
is naturally endowed with a structure of vector space, where 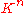 is the set of the ordered sequences of n elements of K. It follows that, in many cases, vector simply refers to a sequence of fixed length of real or complex numbers.
is the set of the ordered sequences of n elements of K. It follows that, in many cases, vector simply refers to a sequence of fixed length of real or complex numbers.
The various uses of vector which follow are special instances of this general definition.
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. If n is a non negative integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
and K is either the field
Field
-Places:* Field, British Columbia, Canada* Field, Minneapolis, Minnesota, United States* Field, Ontario, Canada* Field Island, Nunavut, Canada* Mount Field - Expanses of open ground :* Field...
of the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s or the field of the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
, then
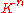 is naturally endowed with a structure of vector space, where
is naturally endowed with a structure of vector space, where 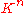 is the set of the ordered sequences of n elements of K. It follows that, in many cases, vector simply refers to a sequence of fixed length of real or complex numbers.
is the set of the ordered sequences of n elements of K. It follows that, in many cases, vector simply refers to a sequence of fixed length of real or complex numbers.The various uses of vector which follow are special instances of this general definition.
Vectors
- Euclidean vector, a geometric entity endowed with both length and direction; an element of a Euclidean vector space. In physics, euclidean vectors are used to represent physical quantities which have both magnitude and direction, such as force, in contrast to scalarScalar (mathematics)In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
quantities, which have no direction.- Vector product, or cross product, an operation on two vectors in a three-dimensional Euclidean space, producing a third three-dimensional Euclidean vector
- Vector projection, also known as the vector resolute, a mapping of one vector onto another
- The vector part of a quaternion, a term used in 19th century mathematical literature on quaternions
- Burgers vectorBurgers vectorThe Burgers vector, named after Dutch physicist Jan Burgers, is a vector, often denoted b, that represents the magnitude and direction of the lattice distortion of dislocation in a crystal lattice....
, a vector that represents the magnitude and direction of the lattice distortion of dislocation in a crystal lattice - Displacement vector, a vector that specifies the change in position of a point relative to a previous position
- Gradient vector, one vector in a vector field
- Laplace–Runge–Lenz vector, a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another
- Normal vector, or surface normal, a vector which is perpendicular to a surface
- Null vectorNull vectorNull vector can refer to:* Null vector * A causal structure in Minkowski space...
, or zero vector, a vector whose components are all zero - Position (vector), a vector which represents the position of an object in space in relation to an arbitrary reference point
- Poynting vectorPoynting vectorIn physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
, in physics, a vector representing the energy flux of an electromagnetic field - Wave vectorWave vectorIn physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
, a vector representation of a wave
- Tangent vectorTangent vectorA tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
, an element of the tangent spaceTangent spaceIn mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
of a curveCurveIn mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
, a surfaceSurfaceIn mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
or, more generally, a differential manifold at a given point. - GyrovectorGyrovector spaceA gyrovector space is a mathematical concept for studying hyperbolic geometry in analogy to the way vector spaces are used in Euclidean geometry. This vector-based approach has been developed by Abraham Albert Ungar from the late 1980s onwards...
, a hyperbolic geometry version of a vector - Axial vector, or pseudovector, a quantity that transforms like a vector under a proper rotation
- Basis vector, one of a set of vectors (a "basis") that, in linear combination, can represent every vector in a given vector space
- Coordinate vectorCoordinate vectorIn linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
, in linear algebra, an explicit representation of an element of any abstract vector space - Darboux vectorDarboux vectorIn differential geometry, especially the theory of space curves, the Darboux vector is the areal velocity vector of the Frenet frame of a space curve. It is named after Gaston Darboux who discovered it...
, the areal velocity vector of the Frenet frame of a space curve - Four-vectorFour-vectorIn the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...
, in the theory of relativity, a vector in a four-dimensional real vector space called Minkowski space - Interval vectorInterval vectorIn musical set theory, an interval vector is an array that expresses the intervallic content of a pitch-class set...
, in musical set theory, an array that expresses the intervallic content of a pitch-class set - P-vector, the tensor obtained by taking linear combinations of the wedge product of p tangent vectors
- Probability vectorProbability vectorStochastic vector redirects here. For the concept of a random vector, see Multivariate random variable.In mathematics and statistics, a probability vector or stochastic vector is a vector with non-negative entries that add up to one....
, in statistics, a vector with non-negative entries that add up to one - Row vector or column vector, a one-dimensional matrix often representing the solution of a system of linear equations
- Spin vector, or Spinor, is an element of a complex vector space introduced to expand the notion of spatial vector
- TupleTupleIn mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
, an ordered list of numbers, sometimes used to represent a vector - Unit vector, a vector in a normed vector space whose length is 1
Vector fields
- Vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
, a construction in vector calculus which associates a vector to every point in a subset of Euclidean space- Conservative vector field, a vector field which is the gradient of a scalar potential field
- Hamiltonian vector fieldHamiltonian vector fieldIn mathematics and physics, a Hamiltonian vector field on a symplectic manifold is a vector field, defined for any energy function or Hamiltonian. Named after the physicist and mathematician Sir William Rowan Hamilton, a Hamiltonian vector field is a geometric manifestation of Hamilton's equations...
, a vector field defined for any energy function or Hamiltonian - Killing vector fieldKilling vector fieldIn mathematics, a Killing vector field , named after Wilhelm Killing, is a vector field on a Riemannian manifold that preserves the metric. Killing fields are the infinitesimal generators of isometries; that is, flows generated by Killing fields are continuous isometries of the manifold...
, a vector field on a Riemannian manifold - Solenoidal vector field, a vector field with zero divergence
- Vector potentialVector potentialIn vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
, a vector field whose curl is a given vector field
- Vector flowVector flowIn mathematics, the vector flow refers to a set of closely related concepts of the flow determined by a vector field. These appear in a number of different contexts, including differential topology, Riemannian geometry and Lie group theory...
, a set of closely related concepts of the flow determined by a vector field
Vector spaces
- Vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, a mathematical structure made up of vectors, objects which may be added with another vector or multiplied by a scalar value- Euclidean vector space, an n-dimensional space with notions of distance and angle that obey the Euclidean relationships
- Dual vector space, a vector space consisting of all linear functionals on another, given vector space
- Graded vector spaceGraded vector spaceIn mathematics, a graded vector space is a type of vector space that includes the extra structure of gradation, which is a decomposition of the vector space into a direct sum of vector subspaces.-N-graded vector spaces:...
, a type of vector space that includes the extra structure of gradation - Normed vector spaceNormed vector spaceIn mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
, a vector space on which a norm is defined - Ordered vector spaceOrdered vector spaceIn mathematics an ordered vector space or partially ordered vector space is a vector space equipped with a partial order which is compatible with the vector space operations.- Definition:...
, a vector space equipped with a partial order - Super vector spaceSuper vector spaceIn mathematics, a super vector space is another name for a Z2-graded vector space, that is, a vector space over a field K with a given decompositionV=V_0\oplus V_1....
, name for a Z2-graded vector space - Symplectic vector spaceSymplectic vector spaceIn mathematics, a symplectic vector space is a vector space V equipped with a bilinear form ω : V × V → R that is...
, a vector space V equipped with a non-degenerate, skew-symmetric, bilinear form - Topological vector spaceTopological vector spaceIn mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
, a blend of topological structure with the algebraic concept of a vector space
Manipulation of vectors, fields, and spaces
- Vector bundleVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
, a topological construction which makes precise the idea of a family of vector spaces parameterized by another space - Vector calculus, a branch of mathematics concerned with differentiation and integration of vector fields
- Vector Analysis, a free, online book on vector calculus first published in 1901 by Edwin Bidwell Wilson
- Vector decompositionVector decompositionVector decomposition refers to decomposing a vector of Rn into several vectors, each linearly independent .-Vector decomposition in two dimensions:...
, refers to decomposing a vector of Rn to several vectors, each linearly independent - Vector differential, or del, is a vector differential operator represented by the nabla symbol:

- Vector LaplacianVector LaplacianIn mathematics and physics, the vector Laplace operator, denoted by \scriptstyle \nabla^2, named after Pierre-Simon Laplace, is a differential operator defined over a vector field. The vector Laplacian is similar to the scalar Laplacian...
, the vector Laplace operator, denoted by is a differential operator defined over a vector field
is a differential operator defined over a vector field - Vector notationVector notationThis page is an overview of the common notations used when working with vectors, which may be spatial or more abstract members of vector spaces....
, common notations used when working with vectors - Vector operator, a type of differential operator used in vector calculus
- Vector product, or cross product, an operation on two vectors in a three-dimensional Euclidean space, producing a third three-dimensional Euclidean vector
- Vector projection, also known as the vector resolute, a mapping of one vector onto another
- Vector-valued functionVector-valued functionA vector-valued function also referred to as a vector function is a mathematical function of one or more variables whose range is a set of multidimensional vectors or infinite-dimensional vectors. The input of a vector-valued function could be a scalar or a vector...
, a mathematical function that maps real numbers to vectors - Vectorization (mathematics)Vectorization (mathematics)In mathematics, especially in linear algebra and matrix theory, the vectorization of a matrix is a linear transformation which converts the matrix into a column vector...
, a linear transformation which converts a matrix into a column vector
Other uses in mathematics and physics
- Vector autoregressionVector autoregressionVector autoregression is a statistical model used to capture the linear interdependencies among multiple time series. VAR models generalize the univariate autoregression models. All the variables in a VAR are treated symmetrically; each variable has an equation explaining its evolution based on...
, an econometric model used to capture the evolution and the interdependencies between multiple time series - Vector bosonVector bosonIn particle physics, a vector boson is a boson with the spin quantum number equal to 1.The vector bosons considered to be elementary particles in the Standard Model are the gauge bosons or, the force carriers of fundamental interactions: the photon of electromagnetism, the W and Z bosons of the...
, a boson with the spin quantum number equal to 1 - Vector measureVector measureIn mathematics, a vector measure is a function defined on a family of sets and taking vector values satisfying certain properties. It is a generalization of the concept of measure, which takes nonnegative real values only.-Definitions and first consequences:...
, a function defined on a family of sets and taking vector values satisfying certain properties - Vector mesonVector mesonIn high energy physics, a vector meson is a meson with total spin 1 and odd parity . Compare to a pseudovector meson, which has a total spin 1 and even parity....
, a meson with total spin 1 and odd parity - Vector quantizationVector quantizationVector quantization is a classical quantization technique from signal processing which allows the modeling of probability density functions by the distribution of prototype vectors. It was originally used for data compression. It works by dividing a large set of points into groups having...
, a quantization technique used in signal processing - Vector solitonVector solitonIn physical optics or wave optics, a vector soliton is a solitary wave with multiple components coupled together that maintains its shape during propagation. Ordinary solitons maintain their shape but have effectively only one polarization component, while vector solitons have two distinct...
, a solitary wave with multiple components coupled together that maintains its shape during propagation - Vector synthesisVector synthesisVector Synthesis is a type of audio synthesis introduced by Sequential Circuits in the Prophet VS synthesizer during 1986. The concept was subsequently used by Yamaha in the SY22/TG33 and similar instruments and by Korg in the Wavestation....
, a type of audio synthesis - Witt vectorWitt vectorIn mathematics, a Witt vector is an infinite sequence of elements of a commutative ring. Ernst Witt showed how to put a ring structure on the set of Witt vectors, in such a way that the ring of Witt vectors over the finite field of order p is the ring of p-adic integers.-Motivation:Any p-adic...
, an infinite sequence of elements of a commutative ring
External Links
- Vectors in physics Includes an embedded interactive program on vectors.

