
Lp space
Encyclopedia
In mathematics
, the Lp spaces are function space
s defined using a natural generalization of the p-norm for finite-dimensional vector space
s. They are sometimes called Lebesgue spaces, named after Henri Lebesgue
, although according to they were first introduced by .
Lp spaces form an important class of Banach space
s in functional analysis
, and of topological vector space
s.
Lebesgue spaces have applications in physics, statistics, finance, engineering, and other disciplines.
 The length of a vector x = (x1, x2, …, xn) in the n-dimensional real
The length of a vector x = (x1, x2, …, xn) in the n-dimensional real
vector space
Rn is usually given by the Euclidean norm .
.
The Euclidean distance between two points x and y is the length of the straight line between the two points.
of the straight line between the two points.
In many situations, the Euclidean distance is insufficient for capturing the actual distances in a given space.
For example, taxi drivers in Manhattan should measure distance not in terms of the length of the straight line to their destination, but in terms of the Manhattan distance, which takes into account that streets are either orthogonal or parallel to each other.
The class of p-norms generalizes these two examples and has an abundance of applications in many parts of mathematics
, physics
, and computer science
.
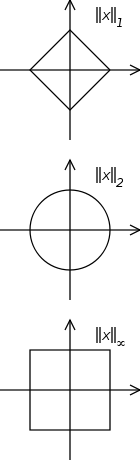
p ≥ 1, the p-norm or Lp-norm of x is defined by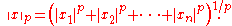
The Euclidean norm from above falls into this class and is the 2-norm, and the 1-norm is the norm that corresponds to the Manhattan distance.
The L∞-norm or maximum norm
(or uniform norm)
is the limit of the Lp-norms for .
.
It turns out that this limit is equivalent to the following definition: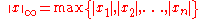 .
.
For all p ≥ 1, the p-norms and maximum norm as defined above indeed satisfy the properties of a "length function" (or norm
), which are that:
Abstractly speaking, this means that Rn together with the p-norm is a Banach space
. This Banach space is the Lp-space over Rn.
Formally, this means that the Euclidean norm of any vector is bounded by its 1-norm: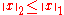 .
.
This fact generalizes to p-norms in that the p-norm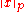 of any given vector x does not grow with p:
of any given vector x does not grow with p: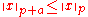 for any vector x and real numbers p ≥ 1 and a ≥ 0.
for any vector x and real numbers p ≥ 1 and a ≥ 0.
For the opposite direction, the following relation between the 1-norm and the 2-norm is known: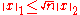 .
.
This inequality depends on the dimension n of the underlying vector space and follows directly from the Cauchy–Schwarz inequality
.

defines an absolutely homogeneous function
for 0 < p < 1; however, the resulting function does not define an F-norm, because it is not subadditive.
In Rn for n > 1, the formula for 0 < p < 1
defines a subadditive function, which does define an F-norm. This F-norm is not homogeneous.
However, the function

defines a metric
. The metric space (Rn, dp) is denoted by ℓnp.
Although the p-unit ball Bnp around the origin in this metric is "concave", the topology defined on Rn by the metric dp is the usual vector space topology of Rn, hence ℓnp is a locally convex topological vector space. Beyond this qualitative statement, a quantitative way to measure the lack of convexity of ℓnp is to denote by Cp(n) the smallest constant C such that the multiple C Bnp of the p-unit ball contains the convex hull of Bnp, equal to Bn1. The fact that Cp(n) = n1/p – 1 tends to infinity with n (for fixed p < 1) reflects the fact that the infinite-dimensional sequence space ℓp defined below, is no longer locally convex.
The mathematical definition of the l0 norm was established by Banach's Theory of Linear Operations. The space
of sequences has a complete metric topology provided by the F–norm
 , which is discussed by Stefan Rolewicz in Metric Linear Spaces. The l0-normed space is studied in functional analysis, probability theory, and harmonic analysis.
, which is discussed by Stefan Rolewicz in Metric Linear Spaces. The l0-normed space is studied in functional analysis, probability theory, and harmonic analysis.
Another function was called the l0 "norm" by David Donoho, whose quotation marks warn that this function is not a proper norm. Some later authors abuse terminology by omitting the quotation marks, alas. Donoho suggested the terminology p-"norm" locally, by taking the limit of the lp norm, on bounded sets, as p approaches zero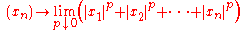
which is the number of non-zero entries of the vector x. Defining 00=0, Donoho's zero "norm" of x is equal to . This is not a norm
. This is not a norm
, because it is not continuous with respect to scalar-vector multiplication (as the scalar approaches zero); it is not a proper norm (B-norm, with "B" for Banach) because it is not homogeneous. Despite these defects as a mathematical norm, Donoho's non-zero counting "norm" (with quotation marks) has uses in scientific computing, information theory
, and statistics
---notably in compressed sensing
in signal processing
and computational harmonic analysis
.

The p-norm can be extended to vectors that have an infinite number of components, which yields the space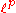 . This contains as special cases:
. This contains as special cases:
The space of sequences has a natural vector space structure by applying addition and scalar multiplication coordinate by coordinate.
Explicitly, for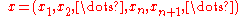 an infinite sequence
an infinite sequence
of real (or complex
) numbers, define the vector sum to be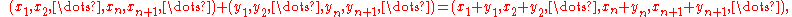
while the scalar action is given by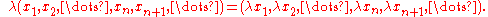
Define the p-norm

Here, a complication arises, namely that the series
on the right is not always convergent, so for example, the sequence made up of only ones, (1, 1, 1, ...), will have an infinite p-norm (length) for every finite p ≥ 1. The space ℓp is then defined as the set of all infinite sequences of real (or complex) numbers such that the p-norm is finite.
One can check that as p increases, the set ℓp grows larger. For example, the sequence
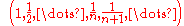
is not in ℓ1, but it is in ℓp for p > 1, as the series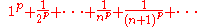
diverges for p = 1 (the harmonic series
), but is convergent for p > 1.
One also defines the ∞-norm as
and the corresponding space ℓ∞ of all bounded sequences. It turns out that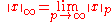
if the right-hand side is finite, or the left-hand side is infinite.
Thus, we will consider ℓp spaces for 1 ≤ p ≤ ∞.
The p-norm thus defined on ℓp is indeed a norm, and ℓp together with this norm is a Banach space
. The fully general Lp space is obtained — as seen below — by considering vectors, not only with finitely or countably-infinitely many components, but with "arbitrarily many components"; in other words, functions
. An integral
instead of a sum is used to define the p-norm.
s from S to C (or R) whose absolute value
raised to the p-th power has finite integral, or equivalently, that
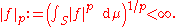
The set of such functions forms a vector space, with the following natural operations:

for every scalar λ.
That the sum of two pth power integrable functions is again pth power integrable follows from the inequality |f + g|p ≤ 2p (|f|p + |g|p). In fact, more is true. Minkowski's inequality
says the triangle inequality
holds for || . ||p. Thus the set of pth power integrable functions, together with the function || . ||p, is a seminormed vector space, which is denoted by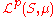 .
.
This can be made into a normed vector space in a standard way; one simply takes the quotient space
with respect to the kernel
of || · ||p. Since for any measurable function f, we have that ||f||p = 0 if and only if f = 0 almost everywhere
, the kernel of || . ||p does not depend upon p,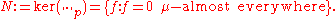
In the quotient space, two functions f and g are identified if f = g almost everywhere. The resulting normed vector space is, by definition,

For p = ∞, the space L∞(S, μ) is defined as follows. We start with the set of all measurable functions from S to C (or R) which are essentially bounded, i.e. bounded up to a set of measure zero. Again two such functions are identified if they are equal almost everywhere. Denote this set by L∞(S, μ). For f in L∞(S, μ), its essential supremum serves as an appropriate norm:
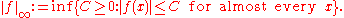
As before, we have

if f ∈ L∞(S, μ) ∩ Lq(S, μ) for some q < ∞.
For 1 ≤ p ≤ ∞, Lp(S, μ) is a Banach space
. The fact that Lp is complete is often referred to as Riesz-Fischer theorem. Completeness can be checked using the convergence theorems for Lebesgue integrals.
When the underlying measure space S is understood, Lp(S, μ) is often abbreviated Lp(μ), or just Lp. The above definitions generalize to Bochner space
s.
of this class. In the complex case, the inner product on L2 is defined by
The additional inner product structure allows for a richer theory, with applications to, for instance, Fourier series
and quantum mechanics
. Functions in L2 are sometimes called quadratically integrable functions, square-integrable functions or square-summable functions, but sometimes these terms are reserved for functions that are square-integrable in some other sense, such as in the sense of a Riemann integral
.
If we use complex-valued functions, the space L∞ is a commutative C*-algebra with pointwise multiplication and conjugation. For many measure spaces, including all sigma-finite ones, it is in fact a commutative von Neumann algebra
. An element of L∞ defines a bounded operator
on any Lp space by multiplication
.
The ℓp spaces (1 ≤ p ≤ ∞) are a special case of Lp spaces, when S is the set N of positive integer
s, and the measure μ is the counting measure
on N. More generally, if one considers any set S with the counting measure, the resulting L p space is denoted ℓp(S). For example, the space ℓp(Z) is the space of all sequences indexed by the integers, and when defining the p-norm on such a space, one sums over all the integers. The space ℓp(n), where n is the set with n elements, is Rn with its p-norm as defined above. As any Hilbert space, every space L2 is linearly isometric to a suitable ℓ2(I), where the cardinality of the set I is the cardinality of an arbitrary Hilbertian basis for this particular L2.
(the space of all continuous linear functionals) of Lp(μ) for 1 < p < ∞ has a natural isomorphism with Lq(μ), where q is such that 1/p + 1/q = 1, which associates g ∈ Lq(μ) with the functional κp(g) ∈ Lp(μ)∗ defined by
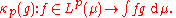
The fact that κp(g) is well defined and continuous follows from Hölder's inequality
. The mapping κp is a linear mapping from Lq(μ) into Lp(μ)∗, which is an isometry
by the extremal case of Hölder's inequality. It is also possible to show (for example with the Radon–Nikodym theorem
, see) that any G ∈ Lp(μ)∗ can be expressed this way: i.e., that κp is onto. Since κp is onto and isometric, it is an isomorphism
of Banach space
s. With this (isometric) isomorphism in mind, it is usual to say simply that Lq "is" the dual of Lp.
When 1 < p < ∞, the space Lp(μ) is reflexive
. Let κp be the above map and let κq be the corresponding linear isometry from Lp(μ) onto Lq(μ)∗. The map
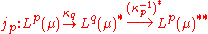
from Lp(μ) to Lp(μ)∗∗, obtained by composing κq with the transpose (or adjoint) of the inverse of κp, coincides with the canonical embedding J of Lp(μ) into its bidual. Moreover, the map jp is onto, as composition of two onto isometries, and this proves reflexivity.
If the measure μ on S is sigma-finite, then the dual of L1(μ) is isometrically isomorphic to L∞(μ) (more precisely, the map κ1 corresponding to p = 1 is an isometry from L∞(μ) onto L1(μ)∗).
The dual of L∞ is subtler. Elements of (L∞(μ))∗ can be identified with bounded signed finitely additive measures on S that are absolutely continuous with respect to μ. See ba space
for more details. If we assume the axiom of choice, this space is much bigger than L1(μ) except in some trivial cases. However, there are relatively consistent extensions of Zermelo-Fraenkel set theory in which the dual of ℓ∞ is ℓ1. This is a result of Shelah, discussed in Eric Schechter's book Handbook of Analysis and its Foundations.
In particular, if the domain S has finite measure, the bound (a consequence of Jensen's inequality
)
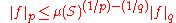
means the space Lq is continuously embedded in Lp. That is to say, the identity operator is a bounded linear map from Lq to Lp. The constant appearing in the above inequality is optimal, in the sense that the operator norm
of the identity I : Lq(S, μ) → Lp(S, μ) is precisely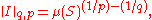
the case of equality being achieved exactly when f = 1 a.e.[μ].
Let (S, Σ, μ) be a measure space. An integrable simple function f on S is one of the form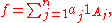
where aj is scalar and Aj ∈ Σ has finite measure, for j = 1,...,n. By construction of the integral
, the vector space of integrable simple functions is dense in Lp(S, Σ, μ).
More can be said when S is a metrizable
topological space
and Σ its Borel σ–algebra
, i.e., the smallest σ–algebra of subsets of S containing the open set
s.
Suppose that V ⊂ S is an open set with μ(V) < ∞. It can be proved that for every Borel set A ∈ Σ contained in V, and for every ε > 0, there exist a closed set F and an open set U such that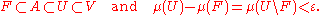
It follows that there exists φ continuous on S such that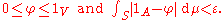
If S can be covered by an increasing sequence (Vn) of open sets that have finite measure, then the space of p–integrable continuous functions is dense in Lp(S, Σ, μ). More precisely, one can use bounded continuous functions that vanish outside one of the open sets Vn.
This applies in particular when S = Rd and when μ is the Lebesgue measure. The space of continuous and compactly supported functions is dense in Lp(Rd). Similarly, the space of integrable step functions is dense in Lp(Rd); this space is the linear span of indicator functions of bounded intervals when d = 1, of bounded rectangles when d = 2 and more generally of products of bounded intervals.
Several properties of general functions in Lp(Rd) are first proved for continuous and compactly supported functions (sometimes for step functions), then extended by density to all functions. For example, it is proved this way that translations are continuous on Lp(Rd), in the following sense: for every f ∈ Lp(Rd),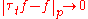
when t ∈ Rd tends to 0, where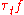 is the translated function defined by
is the translated function defined by 
for the real line (resp. for periodic functions, cf. Fourier series
) maps Lp(R) to Lq(R) (resp. Lp(T) to ℓq), where 1 ≤ p ≤ 2 and 1/p + 1/q = 1. This is a consequence of the Riesz-Thorin interpolation theorem
, and is made precise with the Hausdorff–Young inequality
.
By contrast, if p > 2, the Fourier transform does not map into Lq.
s are central to many applications, from quantum mechanics
to stochastic calculus
. The spaces L2 and ℓ2 are both Hilbert spaces. In fact, by choosing a Hilbert basis, one sees that all Hilbert spaces are isometric to ℓ2(E), where E is a set with an appropriate cardinality.
, measures of central tendency
and statistical dispersion
, such as the mean
, median
, and standard deviation
, are defined in terms of Lp metrics, and measures of central tendency can be characterized as solutions to variational problems.
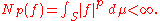
As before, we may introduce the p-norm || f ||p = Np(f)1/p,
but || · ||p does not satisfy the triangle inequality in this case, and defines only a quasi-norm.
The inequality (a + b)p ≤ ap + bp, valid for a ≥ 0 and b ≥ 0 implies that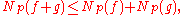
and so the function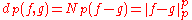
is a metric on Lp(μ). The resulting metric space is complete
; the verification is similar to the familiar case when p ≥ 1.
In this setting Lp satisfies a reverse Minkowski inequality, that is for u and v in Lp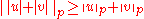 .
.
This result may be used to prove Clarkson's inequalities, which are in turn used to establish the uniform convexity
of the spaces Lp
for 1 < p < ∞ .
The space Lp for 0 < p < 1 is an F-space
: it admits a complete translation-invariant metric with respect to which the vector space operations are continuous. It is also locally bounded, much like the case p ≥ 1. It is the prototypical example of an F-space
that, for most reasonable measure spaces, is not locally convex: in ℓp or
Lp([0, 1]), every open convex set containing the 0 function is unbounded for the p-quasi-norm; therefore, the 0 vector does not possess a fundamental system of convex neighborhoods. Specifically, this is true if the measure space S contains an infinite family of disjoint measurable sets of finite positive measure.
The only nonempty convex open set in Lp([0, 1]) is the entire space . As a particular consequence, there are no nonzero linear functionals on Lp([0, 1]): the dual space is the zero space. In the case of the counting measure
on the natural numbers (producing the sequence space Lp(μ) = ℓp), the bounded linear functionals on ℓp are exactly those that are bounded on ℓ1, namely those given by sequences in ℓ∞. Although ℓp does contain non-trivial convex open sets, it fails to have enough of them to give a base for the topology.
The situation of having no linear functionals is highly undesirable for the purposes of doing analysis. In the case of the Lebesgue measure on Rn, rather than work with Lp for 0 < p < 1, it is common to work with the Hardy space
Hp whenever possible, as this has quite a few linear functionals: enough to distinguish points from one another. However, the Hahn–Banach theorem
still fails in Hp for p < 1 .
. When μ is a probability measure (i.e., μ(S) = 1), this mode of convergence is named convergence in probability.
The description is easier when μ is finite.
If μ is a finite measure on (S, Σ), the 0 function admits for the convergence in measure the following fundamental system of neighborhoods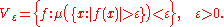
The topology can be defined by any metric d of the form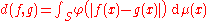
where φ is bounded continuous concave and non-decreasing on [0, ∞), with φ(0) = 0 and φ(t) > 0 when t > 0 (for example, φ(t) = min(t, 1)). Such a metric is called Lévy
-metric for L0. Under this metric the space L0 is complete (it is again an F-space). The space L0 is in general not locally bounded, and not locally convex.
For the infinite Lebesgue measure λ on Rn, the definition of the fundamental system of neighborhoods could be modified as follows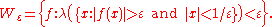
The resulting space L0(Rn, λ) coincides as topological vector space with L0(Rn, g(x) dλ(x)), for any positive λ–integrable density g.
with real or complex values on S. The distribution function
of f is defined for t > 0 by
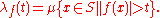
If f is in Lp(S, μ) for some p with 1 ≤ p < ∞, then by Markov's inequality
,
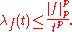
A function f is said to be in the space weak Lp(S, μ), or Lp,w(S, μ), if there is a constant C > 0 such that, for all t > 0,
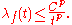
The best constant C for this inequality is the Lp,w-norm of f, and is denoted by
The weak Lp coincide with the Lorentz space
s Lp,∞, so this notation is also used to denote them.
The Lp,w-norm is not a true norm, since the triangle inequality
fails to hold. Nevertheless, for f in Lp(S, μ),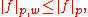
and in particular Lp(S, μ) ⊂ Lp,w(S, μ). Under the convention that two functions are equal if they are equal μ almost everywhere, then the spaces Lp,w are complete .
For any 0 < r < p the expression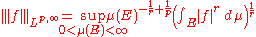
is comparable to the Lp,w-norm. Further in the case p > 1, this expression defines a norm if r = 1. Hence for p > 1 the weak Lp spaces are Banach space
s .
A major result that uses the Lp,w-spaces is the Marcinkiewicz interpolation theorem, which has broad applications to harmonic analysis
and the study of singular integrals.
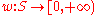 be a measurable function. The w-weighted Lp space is defined as Lp(S, w dμ), where w dμ means the measure ν defined by
be a measurable function. The w-weighted Lp space is defined as Lp(S, w dμ), where w dμ means the measure ν defined by
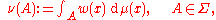
or, in terms of the Radon–Nikodym derivative
,
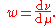
The norm
for Lp(S, w dμ) is explicitly
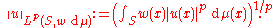
As Lp-spaces, the weighted spaces have nothing special, since Lp(S, w dμ) is equal to Lp(S, dν). But they are the natural framework for several results in harmonic analysis ; they appear for example in the Muckenhoupt theorem: for 1 < p < ∞, the classical Hilbert transform
is defined on Lp(T, λ) where T denotes the unit circle and λ the Lebesgue measure; the (nonlinear) Hardy–Littlewood maximal operator is bounded on Lp(Rn, λ). Muckenhoupt's theorem describes weights w such that the Hilbert transform remains bounded on Lp(T, w dλ) and the maximal operator on Lp(Rn, w dλ).
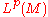 on a manifold, called the intrinsic Lp spaces of the manifold, using densities
on a manifold, called the intrinsic Lp spaces of the manifold, using densities
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Lp spaces are function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
s defined using a natural generalization of the p-norm for finite-dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s. They are sometimes called Lebesgue spaces, named after Henri Lebesgue
Henri Lebesgue
Henri Léon Lebesgue was a French mathematician most famous for his theory of integration, which was a generalization of the seventeenth century concept of integration—summing the area between an axis and the curve of a function defined for that axis...
, although according to they were first introduced by .
Lp spaces form an important class of Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, and of topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s.
Lebesgue spaces have applications in physics, statistics, finance, engineering, and other disciplines.
The p-norm in finite dimensions

Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
Rn is usually given by the Euclidean norm
 .
.The Euclidean distance between two points x and y is the length
 of the straight line between the two points.
of the straight line between the two points.In many situations, the Euclidean distance is insufficient for capturing the actual distances in a given space.
For example, taxi drivers in Manhattan should measure distance not in terms of the length of the straight line to their destination, but in terms of the Manhattan distance, which takes into account that streets are either orthogonal or parallel to each other.
The class of p-norms generalizes these two examples and has an abundance of applications in many parts of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
.
Definition
For a real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
p ≥ 1, the p-norm or Lp-norm of x is defined by
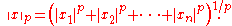
The Euclidean norm from above falls into this class and is the 2-norm, and the 1-norm is the norm that corresponds to the Manhattan distance.
The L∞-norm or maximum norm
Chebyshev distance
In mathematics, Chebyshev distance , Maximum metric, or L∞ metric is a metric defined on a vector space where the distance between two vectors is the greatest of their differences along any coordinate dimension...
(or uniform norm)
is the limit of the Lp-norms for
 .
.It turns out that this limit is equivalent to the following definition:
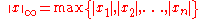 .
.For all p ≥ 1, the p-norms and maximum norm as defined above indeed satisfy the properties of a "length function" (or norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
), which are that:
- only the zero vector has zero length,
- the length of the vector is positive homogeneous with respect to multiplication by a scalar, and
- the length of the sum of two vectors is no larger than the sum of lengths of the vectors (triangle inequalityTriangle inequalityIn mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
).
Abstractly speaking, this means that Rn together with the p-norm is a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
. This Banach space is the Lp-space over Rn.
Relations between p-norms
It is intuitively clear that straight-line distances in Manhattan are generally shorter than taxi distances.Formally, this means that the Euclidean norm of any vector is bounded by its 1-norm:
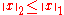 .
.This fact generalizes to p-norms in that the p-norm
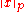 of any given vector x does not grow with p:
of any given vector x does not grow with p: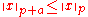 for any vector x and real numbers p ≥ 1 and a ≥ 0.
for any vector x and real numbers p ≥ 1 and a ≥ 0.For the opposite direction, the following relation between the 1-norm and the 2-norm is known:
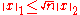 .
.This inequality depends on the dimension n of the underlying vector space and follows directly from the Cauchy–Schwarz inequality
Cauchy–Schwarz inequality
In mathematics, the Cauchy–Schwarz inequality , is a useful inequality encountered in many different settings, such as linear algebra, analysis, probability theory, and other areas...
.
When 0 < p < 1
In Rn for n > 1, the formula
defines an absolutely homogeneous function
Homogeneous function
In mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
for 0 < p < 1; however, the resulting function does not define an F-norm, because it is not subadditive.
In Rn for n > 1, the formula for 0 < p < 1

defines a subadditive function, which does define an F-norm. This F-norm is not homogeneous.
However, the function

defines a metric
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
. The metric space (Rn, dp) is denoted by ℓnp.
Although the p-unit ball Bnp around the origin in this metric is "concave", the topology defined on Rn by the metric dp is the usual vector space topology of Rn, hence ℓnp is a locally convex topological vector space. Beyond this qualitative statement, a quantitative way to measure the lack of convexity of ℓnp is to denote by Cp(n) the smallest constant C such that the multiple C Bnp of the p-unit ball contains the convex hull of Bnp, equal to Bn1. The fact that Cp(n) = n1/p – 1 tends to infinity with n (for fixed p < 1) reflects the fact that the infinite-dimensional sequence space ℓp defined below, is no longer locally convex.
When p = 0
There is one l0 norm and another function called the l0 "norm" (with scare quotation marks).The mathematical definition of the l0 norm was established by Banach's Theory of Linear Operations. The space
F-space
In functional analysis, an F-space is a vector space V over the real or complex numbers together with a metric d : V × V → R so that...
of sequences has a complete metric topology provided by the F–norm
F-space
In functional analysis, an F-space is a vector space V over the real or complex numbers together with a metric d : V × V → R so that...
 , which is discussed by Stefan Rolewicz in Metric Linear Spaces. The l0-normed space is studied in functional analysis, probability theory, and harmonic analysis.
, which is discussed by Stefan Rolewicz in Metric Linear Spaces. The l0-normed space is studied in functional analysis, probability theory, and harmonic analysis.Another function was called the l0 "norm" by David Donoho, whose quotation marks warn that this function is not a proper norm. Some later authors abuse terminology by omitting the quotation marks, alas. Donoho suggested the terminology p-"norm" locally, by taking the limit of the lp norm, on bounded sets, as p approaches zero
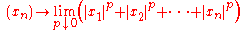
which is the number of non-zero entries of the vector x. Defining 00=0, Donoho's zero "norm" of x is equal to
 . This is not a norm
. This is not a normNorm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
, because it is not continuous with respect to scalar-vector multiplication (as the scalar approaches zero); it is not a proper norm (B-norm, with "B" for Banach) because it is not homogeneous. Despite these defects as a mathematical norm, Donoho's non-zero counting "norm" (with quotation marks) has uses in scientific computing, information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
---notably in compressed sensing
Compressed sensing
Compressed sensing, also known as compressive sensing, compressive sampling and sparse sampling, is a technique for finding sparse solutions to underdetermined linear systems...
in signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
and computational harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
.

The p-norm in countably infinite dimensions
The p-norm can be extended to vectors that have an infinite number of components, which yields the space
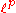 . This contains as special cases:
. This contains as special cases:
-
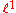 , the space of sequences whose series is absolutely convergentAbsolute convergenceIn mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
, the space of sequences whose series is absolutely convergentAbsolute convergenceIn mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
, -
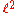 , the space of square-summable sequences, which is a Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, the space of square-summable sequences, which is a Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, and -
 , the space of bounded sequences.
, the space of bounded sequences.
The space of sequences has a natural vector space structure by applying addition and scalar multiplication coordinate by coordinate.
Explicitly, for
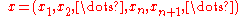 an infinite sequence
an infinite sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of real (or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
) numbers, define the vector sum to be
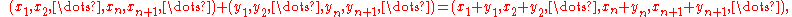
while the scalar action is given by
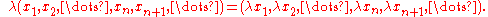
Define the p-norm

Here, a complication arises, namely that the series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
on the right is not always convergent, so for example, the sequence made up of only ones, (1, 1, 1, ...), will have an infinite p-norm (length) for every finite p ≥ 1. The space ℓp is then defined as the set of all infinite sequences of real (or complex) numbers such that the p-norm is finite.
One can check that as p increases, the set ℓp grows larger. For example, the sequence
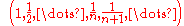
is not in ℓ1, but it is in ℓp for p > 1, as the series
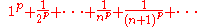
diverges for p = 1 (the harmonic series
Harmonic series (mathematics)
In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
), but is convergent for p > 1.
One also defines the ∞-norm as

and the corresponding space ℓ∞ of all bounded sequences. It turns out that
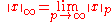
if the right-hand side is finite, or the left-hand side is infinite.
Thus, we will consider ℓp spaces for 1 ≤ p ≤ ∞.
The p-norm thus defined on ℓp is indeed a norm, and ℓp together with this norm is a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
. The fully general Lp space is obtained — as seen below — by considering vectors, not only with finitely or countably-infinitely many components, but with "arbitrarily many components"; in other words, functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
. An integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
instead of a sum is used to define the p-norm.
Lp spaces
Let 1 ≤ p < ∞ and (S, Σ, μ) be a measure space. Consider the set of all measurable functionMeasurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
s from S to C (or R) whose absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
raised to the p-th power has finite integral, or equivalently, that
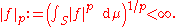
The set of such functions forms a vector space, with the following natural operations:

for every scalar λ.
That the sum of two pth power integrable functions is again pth power integrable follows from the inequality |f + g|p ≤ 2p (|f|p + |g|p). In fact, more is true. Minkowski's inequality
Minkowski inequality
In mathematical analysis, the Minkowski inequality establishes that the Lp spaces are normed vector spaces. Let S be a measure space, let 1 ≤ p ≤ ∞ and let f and g be elements of Lp...
says the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
holds for || . ||p. Thus the set of pth power integrable functions, together with the function || . ||p, is a seminormed vector space, which is denoted by
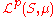 .
.This can be made into a normed vector space in a standard way; one simply takes the quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
with respect to the kernel
Kernel (mathematics)
In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
of || · ||p. Since for any measurable function f, we have that ||f||p = 0 if and only if f = 0 almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
, the kernel of || . ||p does not depend upon p,
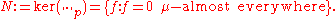
In the quotient space, two functions f and g are identified if f = g almost everywhere. The resulting normed vector space is, by definition,

For p = ∞, the space L∞(S, μ) is defined as follows. We start with the set of all measurable functions from S to C (or R) which are essentially bounded, i.e. bounded up to a set of measure zero. Again two such functions are identified if they are equal almost everywhere. Denote this set by L∞(S, μ). For f in L∞(S, μ), its essential supremum serves as an appropriate norm:
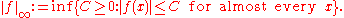
As before, we have

if f ∈ L∞(S, μ) ∩ Lq(S, μ) for some q < ∞.
For 1 ≤ p ≤ ∞, Lp(S, μ) is a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
. The fact that Lp is complete is often referred to as Riesz-Fischer theorem. Completeness can be checked using the convergence theorems for Lebesgue integrals.
When the underlying measure space S is understood, Lp(S, μ) is often abbreviated Lp(μ), or just Lp. The above definitions generalize to Bochner space
Bochner space
In mathematics, Bochner spaces are a generalization of the concept of Lp spaces to functions whose values lie in a Banach space which is not necessarily the space R or C of real or complex numbers....
s.
Special cases
When p = 2; like the ℓ2 space, the space L2 is the only Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
of this class. In the complex case, the inner product on L2 is defined by

The additional inner product structure allows for a richer theory, with applications to, for instance, Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
and quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. Functions in L2 are sometimes called quadratically integrable functions, square-integrable functions or square-summable functions, but sometimes these terms are reserved for functions that are square-integrable in some other sense, such as in the sense of a Riemann integral
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
.
If we use complex-valued functions, the space L∞ is a commutative C*-algebra with pointwise multiplication and conjugation. For many measure spaces, including all sigma-finite ones, it is in fact a commutative von Neumann algebra
Von Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
. An element of L∞ defines a bounded operator
Bounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
on any Lp space by multiplication
Multiplication operator
In operator theory, a multiplication operator is a linear operator T defined on some vector space of functions and whose value at a function φ is given by multiplication by a fixed function f...
.
The ℓp spaces (1 ≤ p ≤ ∞) are a special case of Lp spaces, when S is the set N of positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, and the measure μ is the counting measure
Counting measure
In mathematics, the counting measure is an intuitive way to put a measure on any set: the "size" of a subset is taken to be the number of elements in the subset, if the subset is finite, and ∞ if the subset is infinite....
on N. More generally, if one considers any set S with the counting measure, the resulting L p space is denoted ℓp(S). For example, the space ℓp(Z) is the space of all sequences indexed by the integers, and when defining the p-norm on such a space, one sums over all the integers. The space ℓp(n), where n is the set with n elements, is Rn with its p-norm as defined above. As any Hilbert space, every space L2 is linearly isometric to a suitable ℓ2(I), where the cardinality of the set I is the cardinality of an arbitrary Hilbertian basis for this particular L2.
Dual spaces
The dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
(the space of all continuous linear functionals) of Lp(μ) for 1 < p < ∞ has a natural isomorphism with Lq(μ), where q is such that 1/p + 1/q = 1, which associates g ∈ Lq(μ) with the functional κp(g) ∈ Lp(μ)∗ defined by
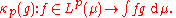
The fact that κp(g) is well defined and continuous follows from Hölder's inequality
Hölder's inequality
In mathematical analysis Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of Lp spaces....
. The mapping κp is a linear mapping from Lq(μ) into Lp(μ)∗, which is an isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
by the extremal case of Hölder's inequality. It is also possible to show (for example with the Radon–Nikodym theorem
Radon–Nikodym theorem
In mathematics, the Radon–Nikodym theorem is a result in measure theory that states that, given a measurable space , if a σ-finite measure ν on is absolutely continuous with respect to a σ-finite measure μ on , then there is a measurable function f on X and taking values in [0,∞), such that\nu =...
, see) that any G ∈ Lp(μ)∗ can be expressed this way: i.e., that κp is onto. Since κp is onto and isometric, it is an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
of Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s. With this (isometric) isomorphism in mind, it is usual to say simply that Lq "is" the dual of Lp.
When 1 < p < ∞, the space Lp(μ) is reflexive
Reflexive space
In functional analysis, a Banach space is called reflexive if it coincides with the dual of its dual space in the topological and algebraic senses. Reflexive Banach spaces are often characterized by their geometric properties.- Normed spaces :Suppose X is a normed vector space over R or C...
. Let κp be the above map and let κq be the corresponding linear isometry from Lp(μ) onto Lq(μ)∗. The map
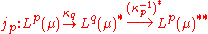
from Lp(μ) to Lp(μ)∗∗, obtained by composing κq with the transpose (or adjoint) of the inverse of κp, coincides with the canonical embedding J of Lp(μ) into its bidual. Moreover, the map jp is onto, as composition of two onto isometries, and this proves reflexivity.
If the measure μ on S is sigma-finite, then the dual of L1(μ) is isometrically isomorphic to L∞(μ) (more precisely, the map κ1 corresponding to p = 1 is an isometry from L∞(μ) onto L1(μ)∗).
The dual of L∞ is subtler. Elements of (L∞(μ))∗ can be identified with bounded signed finitely additive measures on S that are absolutely continuous with respect to μ. See ba space
Ba space
In mathematics, the ba space ba of an algebra of sets \Sigma is the Banach space consisting of all bounded and finitely additive measures on \Sigma. The norm is defined as the variation, that is \|\nu\|=|\nu|....
for more details. If we assume the axiom of choice, this space is much bigger than L1(μ) except in some trivial cases. However, there are relatively consistent extensions of Zermelo-Fraenkel set theory in which the dual of ℓ∞ is ℓ1. This is a result of Shelah, discussed in Eric Schechter's book Handbook of Analysis and its Foundations.
Embeddings
Colloquially, if 1 ≤ p < q ≤ ∞, Lp(S, μ) contains functions that are more locally singular, while elements of Lq(S, μ) can be more spread out. Consider the Lebesgue measure on the half line (0, ∞). A continuous function in L1 might blow up near 0 but must decay sufficiently fast toward infinity. On the other hand, continuous functions in L∞ need not decay at all but no blow-up is allowed. The precise technical result is the following:- Let 1 ≤ p < q ≤ ∞. Lq(S, μ) is contained in Lp(S, μ) iff S does not contain sets of arbitrarily large measure, and
- Let 1 ≤ p < q ≤ ∞. Lp(S, μ) is contained in Lq(S, μ) iff S does not contain sets of arbitrarily small non-zero measure.
In particular, if the domain S has finite measure, the bound (a consequence of Jensen's inequality
Jensen's inequality
In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906. Given its generality, the inequality appears in many forms depending on the context,...
)
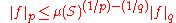
means the space Lq is continuously embedded in Lp. That is to say, the identity operator is a bounded linear map from Lq to Lp. The constant appearing in the above inequality is optimal, in the sense that the operator norm
Operator norm
In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
of the identity I : Lq(S, μ) → Lp(S, μ) is precisely
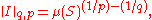
the case of equality being achieved exactly when f = 1 a.e.[μ].
Dense subspaces
It is assumed that 1 ≤ p < ∞ throughout this section.Let (S, Σ, μ) be a measure space. An integrable simple function f on S is one of the form
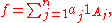
where aj is scalar and Aj ∈ Σ has finite measure, for j = 1,...,n. By construction of the integral
Lebesgue integration
In mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
, the vector space of integrable simple functions is dense in Lp(S, Σ, μ).
More can be said when S is a metrizable
Metrization theorem
In topology and related areas of mathematics, a metrizable space is a topological space that is homeomorphic to a metric space. That is, a topological space is said to be metrizable if there is a metricd\colon X \times X \to [0,\infty)...
topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
and Σ its Borel σ–algebra
Borel algebra
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
, i.e., the smallest σ–algebra of subsets of S containing the open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s.
Suppose that V ⊂ S is an open set with μ(V) < ∞. It can be proved that for every Borel set A ∈ Σ contained in V, and for every ε > 0, there exist a closed set F and an open set U such that
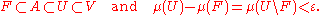
It follows that there exists φ continuous on S such that
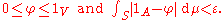
If S can be covered by an increasing sequence (Vn) of open sets that have finite measure, then the space of p–integrable continuous functions is dense in Lp(S, Σ, μ). More precisely, one can use bounded continuous functions that vanish outside one of the open sets Vn.
This applies in particular when S = Rd and when μ is the Lebesgue measure. The space of continuous and compactly supported functions is dense in Lp(Rd). Similarly, the space of integrable step functions is dense in Lp(Rd); this space is the linear span of indicator functions of bounded intervals when d = 1, of bounded rectangles when d = 2 and more generally of products of bounded intervals.
Several properties of general functions in Lp(Rd) are first proved for continuous and compactly supported functions (sometimes for step functions), then extended by density to all functions. For example, it is proved this way that translations are continuous on Lp(Rd), in the following sense: for every f ∈ Lp(Rd),
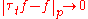
when t ∈ Rd tends to 0, where
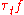 is the translated function defined by
is the translated function defined by 
Hausdorff–Young inequality
The Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
for the real line (resp. for periodic functions, cf. Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
) maps Lp(R) to Lq(R) (resp. Lp(T) to ℓq), where 1 ≤ p ≤ 2 and 1/p + 1/q = 1. This is a consequence of the Riesz-Thorin interpolation theorem
Riesz-Thorin theorem
In mathematics, the Riesz–Thorin theorem, often referred to as the Riesz–Thorin interpolation theorem or the Riesz–Thorin convexity theorem is a result about interpolation of operators. It is named after Marcel Riesz and his student G. Olof Thorin.This theorem bounds the norms of linear maps...
, and is made precise with the Hausdorff–Young inequality
Hausdorff–Young inequality
In mathematics, the Hausdorff−Young inequality bounds the Lq-norm of the Fourier coefficients of a periodic function for q ≥ 2. proved the inequality for some special values of q, and proved it in general...
.
By contrast, if p > 2, the Fourier transform does not map into Lq.
Hilbert spaces
Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s are central to many applications, from quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
to stochastic calculus
Stochastic calculus
Stochastic calculus is a branch of mathematics that operates on stochastic processes. It allows a consistent theory of integration to be defined for integrals of stochastic processes with respect to stochastic processes...
. The spaces L2 and ℓ2 are both Hilbert spaces. In fact, by choosing a Hilbert basis, one sees that all Hilbert spaces are isometric to ℓ2(E), where E is a set with an appropriate cardinality.
Statistics
In statisticsStatistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, measures of central tendency
Central tendency
In statistics, the term central tendency relates to the way in which quantitative data is clustered around some value. A measure of central tendency is a way of specifying - central value...
and statistical dispersion
Statistical dispersion
In statistics, statistical dispersion is variability or spread in a variable or a probability distribution...
, such as the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
, median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
, and standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
, are defined in terms of Lp metrics, and measures of central tendency can be characterized as solutions to variational problems.
Lp for 0 < p < 1
Let (S, Σ, μ) be a measure space. If 0 < p < 1, then Lp(μ) can be defined as above: it is the vector space of those measurable functions f such that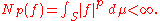
As before, we may introduce the p-norm || f ||p = Np(f)1/p,
but || · ||p does not satisfy the triangle inequality in this case, and defines only a quasi-norm.
The inequality (a + b)p ≤ ap + bp, valid for a ≥ 0 and b ≥ 0 implies that
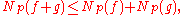
and so the function
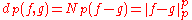
is a metric on Lp(μ). The resulting metric space is complete
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
; the verification is similar to the familiar case when p ≥ 1.
In this setting Lp satisfies a reverse Minkowski inequality, that is for u and v in Lp
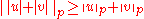 .
.This result may be used to prove Clarkson's inequalities, which are in turn used to establish the uniform convexity
Uniformly convex space
In mathematics, uniformly convex spaces are common examples of reflexive Banach spaces. The concept of uniform convexity was first introduced by James A...
of the spaces Lp
for 1 < p < ∞ .
The space Lp for 0 < p < 1 is an F-space
F-space
In functional analysis, an F-space is a vector space V over the real or complex numbers together with a metric d : V × V → R so that...
: it admits a complete translation-invariant metric with respect to which the vector space operations are continuous. It is also locally bounded, much like the case p ≥ 1. It is the prototypical example of an F-space
F-space
In functional analysis, an F-space is a vector space V over the real or complex numbers together with a metric d : V × V → R so that...
that, for most reasonable measure spaces, is not locally convex: in ℓp or
Lp([0, 1]), every open convex set containing the 0 function is unbounded for the p-quasi-norm; therefore, the 0 vector does not possess a fundamental system of convex neighborhoods. Specifically, this is true if the measure space S contains an infinite family of disjoint measurable sets of finite positive measure.
The only nonempty convex open set in Lp([0, 1]) is the entire space . As a particular consequence, there are no nonzero linear functionals on Lp([0, 1]): the dual space is the zero space. In the case of the counting measure
Counting measure
In mathematics, the counting measure is an intuitive way to put a measure on any set: the "size" of a subset is taken to be the number of elements in the subset, if the subset is finite, and ∞ if the subset is infinite....
on the natural numbers (producing the sequence space Lp(μ) = ℓp), the bounded linear functionals on ℓp are exactly those that are bounded on ℓ1, namely those given by sequences in ℓ∞. Although ℓp does contain non-trivial convex open sets, it fails to have enough of them to give a base for the topology.
The situation of having no linear functionals is highly undesirable for the purposes of doing analysis. In the case of the Lebesgue measure on Rn, rather than work with Lp for 0 < p < 1, it is common to work with the Hardy space
Hardy space
In complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
Hp whenever possible, as this has quite a few linear functionals: enough to distinguish points from one another. However, the Hahn–Banach theorem
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
still fails in Hp for p < 1 .
L0, the space of measurable functions
The vector space of (equivalence classes of) measurable functions on (S, Σ, μ) is denoted L0(S, Σ, μ) . By definition, it contains all the Lp, and is equipped with the topology of convergence in measureConvergence in measure
Convergence in measure can refer to two distinct mathematical concepts which both generalizethe concept of convergence in probability.-Definitions:...
. When μ is a probability measure (i.e., μ(S) = 1), this mode of convergence is named convergence in probability.
The description is easier when μ is finite.
If μ is a finite measure on (S, Σ), the 0 function admits for the convergence in measure the following fundamental system of neighborhoods
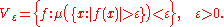
The topology can be defined by any metric d of the form
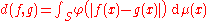
where φ is bounded continuous concave and non-decreasing on [0, ∞), with φ(0) = 0 and φ(t) > 0 when t > 0 (for example, φ(t) = min(t, 1)). Such a metric is called Lévy
Paul Pierre Lévy
Paul Pierre Lévy was a Jewish French mathematician who was active especially in probability theory, introducing martingales and Lévy flights...
-metric for L0. Under this metric the space L0 is complete (it is again an F-space). The space L0 is in general not locally bounded, and not locally convex.
For the infinite Lebesgue measure λ on Rn, the definition of the fundamental system of neighborhoods could be modified as follows
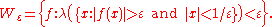
The resulting space L0(Rn, λ) coincides as topological vector space with L0(Rn, g(x) dλ(x)), for any positive λ–integrable density g.
Weak Lp
Let (S, Σ, μ) be a measure space, and f a measurable functionMeasurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
with real or complex values on S. The distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of f is defined for t > 0 by
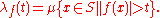
If f is in Lp(S, μ) for some p with 1 ≤ p < ∞, then by Markov's inequality
Markov's inequality
In probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
,
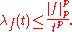
A function f is said to be in the space weak Lp(S, μ), or Lp,w(S, μ), if there is a constant C > 0 such that, for all t > 0,
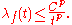
The best constant C for this inequality is the Lp,w-norm of f, and is denoted by

The weak Lp coincide with the Lorentz space
Lorentz space
In mathematical analysis, Lorentz spaces, introduced by George Lorentz in the 1950s, are generalisations of the more familiar Lp spaces.The Lorentz spaces are denoted by Lp,q. Like the Lp spaces, they are characterized by a norm that encodes information about the "size" of a function, just as the...
s Lp,∞, so this notation is also used to denote them.
The Lp,w-norm is not a true norm, since the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
fails to hold. Nevertheless, for f in Lp(S, μ),
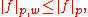
and in particular Lp(S, μ) ⊂ Lp,w(S, μ). Under the convention that two functions are equal if they are equal μ almost everywhere, then the spaces Lp,w are complete .
For any 0 < r < p the expression
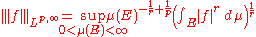
is comparable to the Lp,w-norm. Further in the case p > 1, this expression defines a norm if r = 1. Hence for p > 1 the weak Lp spaces are Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s .
A major result that uses the Lp,w-spaces is the Marcinkiewicz interpolation theorem, which has broad applications to harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
and the study of singular integrals.
Weighted Lp spaces
As before, consider a measure space (S, Σ, μ). Let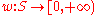 be a measurable function. The w-weighted Lp space is defined as Lp(S, w dμ), where w dμ means the measure ν defined by
be a measurable function. The w-weighted Lp space is defined as Lp(S, w dμ), where w dμ means the measure ν defined by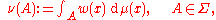
or, in terms of the Radon–Nikodym derivative
Radon–Nikodym theorem
In mathematics, the Radon–Nikodym theorem is a result in measure theory that states that, given a measurable space , if a σ-finite measure ν on is absolutely continuous with respect to a σ-finite measure μ on , then there is a measurable function f on X and taking values in [0,∞), such that\nu =...
,
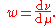
The norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
for Lp(S, w dμ) is explicitly
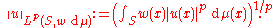
As Lp-spaces, the weighted spaces have nothing special, since Lp(S, w dμ) is equal to Lp(S, dν). But they are the natural framework for several results in harmonic analysis ; they appear for example in the Muckenhoupt theorem: for 1 < p < ∞, the classical Hilbert transform
Hilbert transform
In mathematics and in signal processing, the Hilbert transform is a linear operator which takes a function, u, and produces a function, H, with the same domain. The Hilbert transform is named after David Hilbert, who first introduced the operator in order to solve a special case of the...
is defined on Lp(T, λ) where T denotes the unit circle and λ the Lebesgue measure; the (nonlinear) Hardy–Littlewood maximal operator is bounded on Lp(Rn, λ). Muckenhoupt's theorem describes weights w such that the Hilbert transform remains bounded on Lp(T, w dλ) and the maximal operator on Lp(Rn, w dλ).
Lp spaces on manifolds
One may also define spaces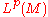 on a manifold, called the intrinsic Lp spaces of the manifold, using densities
on a manifold, called the intrinsic Lp spaces of the manifold, using densitiesDensity on a manifold
In mathematics, and specifically differential geometry, a density is a spatially varying quantity on a differentiable manifold which can be integrated in an intrinsic manner. Abstractly, a density is a section of a certain trivial line bundle, called the density bundle...
.
See also
- Birnbaum–Orlicz spaceBirnbaum–Orlicz spaceIn the mathematical analysis, and especially in real and harmonic analysis, a Birnbaum–Orlicz space is a type of function space which generalizes the Lp spaces. Like the Lp spaces, they are Banach spaces...
- Hardy spaceHardy spaceIn complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
- Hölder mean
- Hölder space
- Root mean squareRoot mean squareIn mathematics, the root mean square , also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity. It is especially useful when variates are positive and negative, e.g., sinusoids...
- Locally integrable functionLocally integrable functionIn mathematics, a locally integrable function is a function which is integrable on any compact set of its domain of definition. Their importance lies on the fact that we do not care about their behavior at infinity.- Formal definition :...
( )
) -
 spaces over a locally compact group
spaces over a locally compact group 

