.gif)
Parallel (geometry)
Encyclopedia
Parallelism is a term in geometry
and in everyday life that refers to a property in Euclidean space
of two or more line
s or planes
, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid
's parallel postulate
. Two lines in a plane that do not intersect or touch at a point are called parallel lines. Likewise, a line and a plane, or two planes, in three-dimensional Euclidean space that do not share a point are said to be parallel.
In a non-Euclidean space
, parallel lines are those that intersect only in the limit at infinity.
. For example, 
indicates that line AB is parallel to line CD.
In the Unicode
character set, the 'parallel' and 'not parallel' signs have codepoints U+2225 (∥) and U+2226 (∦) respectively.
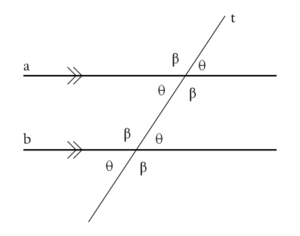Given straight lines l and m, the following descriptions of line m equivalently define it as parallel to line l in Euclidean space
:
In other words, parallel lines must be located in the same plane, and parallel planes must be located in the same three-dimensional space. A parallel combination of a line and a plane may be located in the same three-dimensional space. Lines parallel to each other have the same gradient. Compare to perpendicular
.
Another definition of parallel line that's often used is that two lines are parallel if they do not intersect, though this definition applies only in the 2-dimensional plane. Another easy way is to remember that a parallel line is a line that has an equal distance with the opposite line.
the distance between the two lines can be found by solving the linear system of:
and the system of:
to get the coordinates of the points. The solution to the linear systems are:
Putting into the distance formula gives us:
...
which of course, is:
Also if 2 lines are
the distance between the two lines can be formulated by the following formula:
it is more common to talk about geodesic
s than (straight) lines. A geodesic is the path that a particle follows if no force is applied to it. In non-Euclidean geometry (spherical
or hyperbolic
) the three Euclidean definitions are not equivalent: only the second one is useful in other non-Euclidean geometries. In general, equidistant
lines are not geodesics so the equidistant definition cannot be used. In the Euclidean plane, when two geodesics (straight lines) are intersected with the same angles by a transversal geodesic (see image), every (non-parallel) geodesic intersects them with the same angles. In both the hyperbolic and spherical plane, this is not the case. For example, geodesics sharing a common perpendicular only do so at one point (hyperbolic space) or at two (antipodal) points (spherical space).
In general geometry it is useful to distinguish the three definitions above as three different types of lines, respectively equidistant lines, parallel geodesics and geodesics sharing a common perpendicular.
While in Euclidean geometry two geodesics can either intersect or be parallel, in general and in hyperbolic space in particular there are three possibilities. Two geodesics can be either:
In the literature ultra parallel geodesics are often called parallel. Geodesics intersecting at infinity are then called limit geodesics.
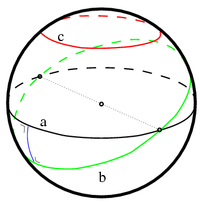In the spherical plane
, all geodesics are great circles. Great circles divide the sphere in two equal hemispheres
and all great circles intersect each other. By the above definitions, there are no parallel geodesics to a given geodesic, all geodesics intersect. Equidistant lines on the sphere are called parallels of latitude in analog to latitude
lines on a globe. Parallel lines in Euclidean space are straight lines; equidistant lines are not geodesics and therefore are not directly analogous to straight lines in the Euclidean space. An object traveling along such a line has to accelerate away from the geodesic to which it is equidistant to avoid intersecting with it. When embedded in Euclidean space a dimension
higher, parallels of latitude can be generated by the intersection of the sphere with a plane parallel to a plane through the center.
, there are two lines through a given point that intersect a given line in the limit to infinity. While in Euclidean geometry a geodesic intersects its parallels in both directions in the limit to infinity, in hyperbolic geometry both directions have their own line of parallelism. When visualized on a plane a geodesic is said to have a left-handed parallel and a right-handed parallel through a given point. The angle the parallel lines make with the perpendicular from that point to the given line is called the angle of parallelism
. The angle of parallelism depends on the distance of the point to the line with respect to the curvature
of the space. The angle is also present in the Euclidean case, there it is always 90° so the left and right-handed parallels coincide
. The parallel lines divide the set of geodesics through the point in two sets: intersecting geodesics that intersect the given line in the hyperbolic plane, and ultra parallel geodesics that do not intersect even in the limit to infinity (in either direction). In the Euclidean limit the latter set is empty.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and in everyday life that refers to a property in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
of two or more line
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
s or planes
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
's parallel postulate
Parallel postulate
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
. Two lines in a plane that do not intersect or touch at a point are called parallel lines. Likewise, a line and a plane, or two planes, in three-dimensional Euclidean space that do not share a point are said to be parallel.
In a non-Euclidean space
Non-Euclidean geometry
Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
, parallel lines are those that intersect only in the limit at infinity.
Symbol
The parallel symbol is . For example, indicates that line AB is parallel to line CD.In the Unicode
Unicode
Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems...
character set, the 'parallel' and 'not parallel' signs have codepoints U+2225 (∥) and U+2226 (∦) respectively.
Euclidean parallelism
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
:
- Every point on line m is located at exactly the same minimum distance from line l (equidistant lines).
- Line m is on the same plane as line l but does not intersect l (even assuming that lines extend to infinityInfinityInfinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
in either direction). - Lines m and l are both intersected by a third straight line (a transversalTransversal (geometry)In geometry, a transversal is a line that passes through two or more other lines in the same plane at different points. When the lines are parallel, as is often the case, a transversal produces several congruent and several supplementary angles...
) in the same plane, and the corresponding angles of intersection with the transversal are equal. (This is equivalent to EuclidEuclidEuclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
's parallel postulateParallel postulateIn geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
.)
In other words, parallel lines must be located in the same plane, and parallel planes must be located in the same three-dimensional space. A parallel combination of a line and a plane may be located in the same three-dimensional space. Lines parallel to each other have the same gradient. Compare to perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
.
Construction
The three definitions above lead to three different methods of construction of parallel lines.Another definition of parallel line that's often used is that two lines are parallel if they do not intersect, though this definition applies only in the 2-dimensional plane. Another easy way is to remember that a parallel line is a line that has an equal distance with the opposite line.
Distance between two parallel lines
Because a parallel line is a line that has an equal distance with the opposite line, there is a unique distance between the two parallel lines. Given the equations of two non-vertical parallel lines:
the distance between the two lines can be found by solving the linear system of:
and the system of:
to get the coordinates of the points. The solution to the linear systems are:
Putting into the distance formula gives us:
...
which of course, is:
Also if 2 lines are
the distance between the two lines can be formulated by the following formula:
Extension to non-Euclidean geometry
In non-Euclidean geometryNon-Euclidean geometry
Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
it is more common to talk about geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s than (straight) lines. A geodesic is the path that a particle follows if no force is applied to it. In non-Euclidean geometry (spherical
Elliptic geometry
Elliptic geometry is a non-Euclidean geometry, in which, given a line L and a point p outside L, there exists no line parallel to L passing through p. Elliptic geometry, like hyperbolic geometry, violates Euclid's parallel postulate, which can be interpreted as asserting that there is exactly one...
or hyperbolic
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
) the three Euclidean definitions are not equivalent: only the second one is useful in other non-Euclidean geometries. In general, equidistant
Equidistant
A point is said to be equidistant from a set of objects if the distances between that point and each object in the set are equal.In two-dimensional Euclidian geometry the locus of points equidistant from two given points is their perpendicular bisector...
lines are not geodesics so the equidistant definition cannot be used. In the Euclidean plane, when two geodesics (straight lines) are intersected with the same angles by a transversal geodesic (see image), every (non-parallel) geodesic intersects them with the same angles. In both the hyperbolic and spherical plane, this is not the case. For example, geodesics sharing a common perpendicular only do so at one point (hyperbolic space) or at two (antipodal) points (spherical space).
In general geometry it is useful to distinguish the three definitions above as three different types of lines, respectively equidistant lines, parallel geodesics and geodesics sharing a common perpendicular.
While in Euclidean geometry two geodesics can either intersect or be parallel, in general and in hyperbolic space in particular there are three possibilities. Two geodesics can be either:
- intersecting: they intersect in a common point in the plane
- parallel: they do not intersect in the plane, but do in the limit to infinity
- ultra parallel: they do not even intersect in the limit to infinity
In the literature ultra parallel geodesics are often called parallel. Geodesics intersecting at infinity are then called limit geodesics.
Spherical
Spherical geometry
Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....
, all geodesics are great circles. Great circles divide the sphere in two equal hemispheres
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
and all great circles intersect each other. By the above definitions, there are no parallel geodesics to a given geodesic, all geodesics intersect. Equidistant lines on the sphere are called parallels of latitude in analog to latitude
Latitude
In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
lines on a globe. Parallel lines in Euclidean space are straight lines; equidistant lines are not geodesics and therefore are not directly analogous to straight lines in the Euclidean space. An object traveling along such a line has to accelerate away from the geodesic to which it is equidistant to avoid intersecting with it. When embedded in Euclidean space a dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
higher, parallels of latitude can be generated by the intersection of the sphere with a plane parallel to a plane through the center.
Hyperbolic
In the hyperbolic planeHyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
, there are two lines through a given point that intersect a given line in the limit to infinity. While in Euclidean geometry a geodesic intersects its parallels in both directions in the limit to infinity, in hyperbolic geometry both directions have their own line of parallelism. When visualized on a plane a geodesic is said to have a left-handed parallel and a right-handed parallel through a given point. The angle the parallel lines make with the perpendicular from that point to the given line is called the angle of parallelism
Angle of parallelism
In hyperbolic geometry, the angle of parallelism φ, also known as Π, is the angle at one vertex of a right hyperbolic triangle that has two asymptotic parallel sides. The angle depends on the segment length a between the right angle and the vertex of the angle of parallelism φ...
. The angle of parallelism depends on the distance of the point to the line with respect to the curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of the space. The angle is also present in the Euclidean case, there it is always 90° so the left and right-handed parallels coincide
Coincident
Coincident is a geometric term that pertains to the relationship between two vectors. Vectors consist of a "magnitude" and a "direction". Vectors can be said to be coincident when their direction is the same though the magnitude may be different; that is to say, they lie one on top of the other...
. The parallel lines divide the set of geodesics through the point in two sets: intersecting geodesics that intersect the given line in the hyperbolic plane, and ultra parallel geodesics that do not intersect even in the limit to infinity (in either direction). In the Euclidean limit the latter set is empty.