Riesz space
Encyclopedia
In mathematics
a Riesz space, lattice-ordered vector space or vector lattice is an ordered vector space
where the order structure is a lattice
.
Riesz spaces are named after Frigyes Riesz
who first defined them in his 1928 paper Sur la décomposition des opérations fonctionelles linéaires.
Riesz spaces are important in measure theory, in that important results are special cases of results for Riesz Spaces. E.g. the Radon-Nikodym theorem follows as a special case of the Freudenthal spectral theorem.
and 
. Then it can be shown that, 
and an absolute value can be defined by 
.
Bands and
A band B in a Riesz space E is defined to be an ideal with the extra property, that for any element f in E for which its absolute value |f| is the supremum of an arbitrary subset of positive elements in B, that f is actually in B. 
-Ideals are defined similarly, with the words 'arbitrary subset' replaced with 'countable subset'. Clearly every band is a 
-ideal, but the converse is not true in general.
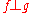, when 
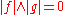. For any subset A of E, its disjoint complement 
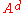is defined as the set of all elements in E, that are disjoint to all elements in A. Disjoint complements are always bands, but the converse is not true in general.
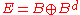, meaning every element f in E, can be written uniquely as a sum of two elements, 
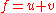, with 
and 
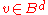. There then also exists a positive linear idempotent, or projection, 
, such that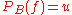 
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
a Riesz space, lattice-ordered vector space or vector lattice is an ordered vector space
Ordered vector space
In mathematics an ordered vector space or partially ordered vector space is a vector space equipped with a partial order which is compatible with the vector space operations.- Definition:...
where the order structure is a lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
.
Riesz spaces are named after Frigyes Riesz
Frigyes Riesz
Frigyes Riesz was a mathematician who was born in Győr, Hungary and died in Budapest, Hungary. He was rector and professor at University of Szeged...
who first defined them in his 1928 paper Sur la décomposition des opérations fonctionelles linéaires.
Riesz spaces are important in measure theory, in that important results are special cases of results for Riesz Spaces. E.g. the Radon-Nikodym theorem follows as a special case of the Freudenthal spectral theorem.
Definition
A Riesz space E is defined to be a vector space endowed with a compatible ordered lattice structure. Specifically, every finite subset of E has a supremum and infimum.Basic properties
Every element f in E has unique positive and negative parts, written and . Then it can be shown that, and an absolute value can be defined by .Subspaces
Being vector spaces, it is also interesting to consider subspaces of Riesz spaces. The extra structure provided by these spaces provide for distinct kinds of Riesz subspaces.Ideals
A vector subspace I of a Riesz space E is called an ideal if it is solid, meaning if for any element f in I and any g in E, |g| ≤ |f| implies that g is actually in I. Bands and 
-Ideals
A band B in a Riesz space E is defined to be an ideal with the extra property, that for any element f in E for which its absolute value |f| is the supremum of an arbitrary subset of positive elements in B, that f is actually in B. -Ideals are defined similarly, with the words 'arbitrary subset' replaced with 'countable subset'. Clearly every band is a -ideal, but the converse is not true in general.Disjoint complements
Two elements f,g in a Riesz space E, are said to be disjoint, written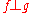, when 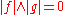. For any subset A of E, its disjoint complement 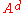is defined as the set of all elements in E, that are disjoint to all elements in A. Disjoint complements are always bands, but the converse is not true in general.Projection bands
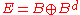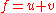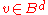A band B in a Riesz space, is called a projection band, if, meaning every element f in E, can be written uniquely as a sum of two elements, , with and . There then also exists a positive linear idempotent, or projection, , such that 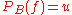.Examples
- The space of continuous real valued function on a set X with compact support with the pointwisePointwiseIn mathematics, the qualifier pointwise is used to indicate that a certain property is defined by considering each value f of some function f. An important class of pointwise concepts are the pointwise operations — operations defined on functions by applying the operations to function values...
partial order defined by f ≤ g when f(x) ≤ g(x) for all x in X, is a Riesz space.
Properties
- Riesz spaces are lattice ordered groups
- Every Riesz space is a distributive latticeDistributive latticeIn mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...