
Simplex
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a simplex (plural simplexes or simplices) is a generalization of the notion of a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
or tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
to arbitrary dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
. Specifically, an n-simplex is an n-dimensional polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
which is the convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of its n + 1 vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron, and a 4-simplex is a pentachoron
Pentachoron
In geometry, the 5-cell is a four-dimensional object bounded by 5 tetrahedral cells. It is also known as the pentachoron, pentatope, or hyperpyramid...
. A single point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
may be considered a 0-simplex, and a line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
may be considered a 1-simplex. A simplex may be defined as the smallest convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
containing the given vertices.
A regular simplex is a simplex that is also a regular polytope
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
. A regular n-simplex may be constructed from a regular (n − 1)-simplex by connecting a new vertex to all original vertices by the common edge length.
In topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, it is common to “glue together” simplices to form a simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
. The associated combinatorial structure is called an abstract simplicial complex
Abstract simplicial complex
In mathematics, an abstract simplicial complex is a purely combinatorial description of the geometric notion of a simplicial complex, consisting of a family of finite sets closed under the operation of taking subsets...
, in which context the word “simplex” simply means any finite set of vertices.
Elements
The convex hull of any nonempty subset of the n+1 points that define an n-simplex is called a face of the simplex. Faces are simplices themselves. In particular, the convex hull of a subset of size m+1 (of the n+1 defining points) is an m-simplex, called an m-face of the n-simplex. The 0-faces (i.e., the defining points themselves as sets of size 1) are called the vertices (singular: vertex), the 1-faces are called the edges, the (n − 1)-faces are called the facets, and the sole n-face is the whole n-simplex itself. In general, the number of m-faces is equal to the binomial coefficientBinomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
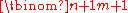 . Consequently, the number of m-faces of an n-simplex may be found in column (m + 1) of row (n + 1) of Pascal's triangle
. Consequently, the number of m-faces of an n-simplex may be found in column (m + 1) of row (n + 1) of Pascal's trianglePascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
. A simplex A is a coface of a simplex B if B is a face of A. Face and facet can have different meanings when describing types of simplices in a simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
. See Simplicial complex#Definitions
The regular simplex family is the first of three regular polytope
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
families, labeled by Coxeter as αn, the other two being the cross-polytope
Cross-polytope
In geometry, a cross-polytope, orthoplex, hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of . The cross-polytope is the convex hull of its vertices...
family, labeled as βn, and the hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
s, labeled as γn. A fourth family, the infinite tessellation of hypercubes, he labeled as δn.
The number of 1-faces (edges) of the n-simplex is the (n-1)th triangle number, the number of 2-faces (faces) of the n-simplex is the (n-2)th tetrahedron number, the number of 3-faces (cells) of the n-simplex is the (n-3)th pentachoron number, and so on.
| Δn | Name | Schläfli symbol Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
0- faces (vertices) |
1- faces (edges) |
2- faces (faces) |
3- faces (cells) |
4- faces |
5- faces |
6- faces |
7- faces |
8- faces |
9- faces |
10- faces |
Sum =2n+1-1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Δ0 | 0-simplex (point Vertex (geometry) In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:... ) |
1 | 1 | |||||||||||
| Δ1 | 1-simplex (line segment Edge (geometry) In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects.... ) |
{} |
2 | 1 | 3 | |||||||||
| Δ2 | 2-simplex (triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... ) |
{3} |
3 | 3 | 1 | 7 | ||||||||
| Δ3 | 3-simplex (tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... ) |
{3,3} |
4 | 6 | 4 | 1 | 15 | |||||||
| Δ4 | 4-simplex (pentachoron Pentachoron In geometry, the 5-cell is a four-dimensional object bounded by 5 tetrahedral cells. It is also known as the pentachoron, pentatope, or hyperpyramid... ) |
{3,3,3} |
5 | 10 | 10 | 5 | 1 | 31 | ||||||
| Δ5 | 5-simplex (hexateron Hexateron In five dimensional geometry, a 5-simplex is a self-dual regular 5-polytope. It has 6 vertices, 15 edges, 20 triangle faces, 15 tetrahedral cells, and 6 pentachoron facets. It has a dihedral angle of cos−1, or approximately 78.46°.- Alternate names :... ) |
{3,3,3,3} |
6 | 15 | 20 | 15 | 6 | 1 | 63 | |||||
| Δ6 | 6-simplex (heptapeton Heptapeton In geometry, a 6-simplex is a self-dual regular 6-polytope. It has 7 vertices, 21 edges, 35 triangle faces, 35 tetrahedral cells, 21 5-cell 4-faces, and 7 5-simplex 5-faces. Its dihedral angle is cos−1, or approximately 80.41°.- Alternate names :... ) |
{3,3,3,3,3} |
7 | 21 | 35 | 35 | 21 | 7 | 1 | 127 | ||||
| Δ7 | 7-simplex (octaexon Octaexon In 7-dimensional geometry, a 7-simplex is a self-dual regular 7-polytope. It has 8 vertices, 28 edges, 56 triangle faces, 70 tetrahedral cells, 56 5-cell 5-faces, 28 5-simplex 6-faces, and 8 6-simplex 7-faces. Its dihedral angle is cos−1, or approximately 81.79°.- Alternate names :It can also be... ) |
{3,3,3,3,3,3} |
8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | 255 | |||
| Δ8 | 8-simplex (enneazetton Enneazetton In geometry, an 8-simplex is a self-dual regular 8-polytope. It has 9 vertices, 36 edges, 84 triangle faces, 126 tetrahedral cells, 126 5-cell 4-faces, 84 5-simplex 5-faces, 36 6-simplex 6-faces, and 9 7-simplex 7-faces. Its dihedral angle is cos−1, or approximately 82.82°.It can also be called an... ) |
{3,3,3,3,3,3,3} |
9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 | 511 | ||
| Δ9 | 9-simplex (decayotton Decayotton In geometry, a 9-simplex is a self-dual regular 9-polytope. It has 10 vertices, 45 edges, 120 triangle faces, 210 tetrahedral cells, 252 5-cell 4-faces, 210 5-simplex 5-faces, 120 6-simplex 6-faces, 45 7-simplex 7-faces, and 10 8-simplex 8-faces... ) |
{3,3,3,3,3,3,3,3} |
10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 | 1023 | |
| Δ10 | 10-simplex 10-simplex In geometry, a 10-simplex is a self-dual regular 10-polytope. It has 11 vertices, 55 edges, 165 triangle faces, 330 tetrahedral cells, 462 5-cell 4-faces, 462 5-simplex 5-faces, 330 6-simplex 6-faces, 165 7-simplex 7-faces, 55 8-simplex 8-faces, and 11 9-simplex 9-faces... (hendecaxennon) |
{3,3,3,3,3,3,3,3,3} |
11 | 55 | 165 | 330 | 462 | 462 | 330 | 165 | 55 | 11 | 1 | 2047 |
 |
In some conventions, the empty set is defined to be a (−1)-simplex. The definition of the simplex above still makes sense if n = −1. This convention is more common in applications to algebraic topology (such as simplicial homology
Simplicial homology
In mathematics, in the area of algebraic topology, simplicial homology is a theory with a finitary definition, and is probably the most tangible variant of homology theory....
) than to the study of polytopes.
Symmetric graphs of regular simplices
These Petrie polygonPetrie polygon
In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon such that every consecutive sides belong to one of the facets...
(skew orthogonal projections) show all the vertices of the regular simplex on a circle, and all vertex pairs connected by edges.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
The standard simplex
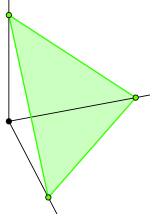
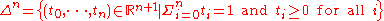
The simplex Δn lies in the affine hyperplane obtained by removing the restriction ti ≥ 0 in the above definition. The standard simplex is clearly regular.
The n+1 vertices of the standard n-simplex are the points {ei} ⊂ Rn+1, where
- e0 = (1, 0, 0, ..., 0),
- e1 = (0, 1, 0, ..., 0),

- en = (0, 0, 0, ..., 1).
There is a canonical map from the standard n-simplex to an arbitrary n-simplex with vertices (v0, …, vn) given by
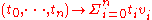
The coefficients ti are called the barycentric coordinates
Barycentric coordinates (mathematics)
In geometry, the barycentric coordinate system is a coordinate system in which the location of a point is specified as the center of mass, or barycenter, of masses placed at the vertices of a simplex . Barycentric coordinates are a form of homogeneous coordinates...
of a point in the n-simplex. Such a general simplex is often called an affine n-simplex, to emphasize that the canonical map is an affine transformation
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
. It is also sometimes called an oriented affine n-simplex to emphasize that the canonical map may be orientation preserving
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
or reversing.
More generally, there is a canonical map from the standard
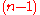 -simplex (with n vertices) onto any polytope
-simplex (with n vertices) onto any polytopePolytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
with n vertices, given by the same equation (modifying indexing):
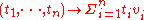
These are known as generalized barycentric coordinates, and express every polytope as the image of a simplex:
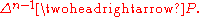
Increasing coordinates
An alternative coordinate system is given by taking the indefinite sum: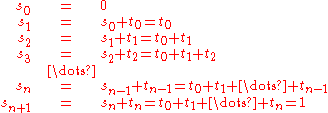
This yields the alternative presentation by order, namely as nondecreasing n-tuples between 0 and 1:
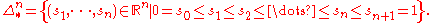
Geometrically, this is an n-dimensional subset of
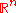 (maximal dimension, codimension 0) rather than of
(maximal dimension, codimension 0) rather than of  (codimension 1). The hyperfaces, which on the standard simplex correspond to one coordinate vanishing,
(codimension 1). The hyperfaces, which on the standard simplex correspond to one coordinate vanishing,  here correspond to successive coordinates being equal,
here correspond to successive coordinates being equal,  while the interior corresponds to the inequalities becoming strict (increasing sequences).
while the interior corresponds to the inequalities becoming strict (increasing sequences).A key distinction between these presentations is the behavior under permuting coordinates – the standard simplex is stabilized by permuting coordinates, while permuting elements of the "ordered simplex" do not leave it invariant, as permuting an ordered sequence generally makes it unordered. Indeed, the ordered simplex is a (closed) fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
for the action of the symmetric group on the n-cube, meaning that the orbit of the ordered simplex under the n! elements of the symmetric group divides the n-cube into
 mostly disjoint simplices (disjoint except for boundaries), showing that this simplex has volume
mostly disjoint simplices (disjoint except for boundaries), showing that this simplex has volume 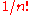 Alternatively, the volume can be computed by an iterated integral, whose successive integrands are
Alternatively, the volume can be computed by an iterated integral, whose successive integrands are 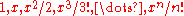
A further property of this presentation is that it uses the order but not addition, and thus can be defined in any dimension over any ordered set, and for example can be used to define an infinite-dimensional simplex without issues of convergence of sums.
Projection onto the standard simplex
Especially in numerical applications of probability theoryProbability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
a projection
Projection
Projection, projector, or projective may refer to:* The display of an image by devices such as:** Movie projector** Video projector** Overhead projector** Slide projector** Camera obscura** Projection screen...
onto the standard simplex is of interest. Given
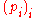 with possibly negative entries, the closest point
with possibly negative entries, the closest point 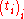 on the simplex has coordinates
on the simplex has coordinates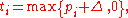
where
 is chosen such that
is chosen such that 
Corner of cube
Finally, a simple variant is to replace "summing to 1" with "summing to at most 1"; this raises the dimension by 1, so to simplify notation, the indexing changes: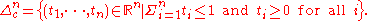
This yields an n-simplex as a corner of the n-cube, and is a standard orthogonal simplex. This is the simplex used in the simplex method, which is based at the origin, and locally models a vertex on a polytope with n faces.
Cartesian coordinates for regular n-dimensional simplex in Rn
The coordinates of the vertices of a regular n-dimensional simplex can be obtained from these two properties,- For a regular simplex, the distances of its vertices to its center are equal.
- The angle subtended by any two vertices of an n-dimensional simplex through its center is

These can be used as follows. Let vectors (v0, v1, ..., vn) represent the vertices of an n-simplex center the origin, all unit vectors so a distance 1 from the origin, satisfying the first property. The second property means the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
between any pair of the vectors is -. This can be used to calculate positions for them.
For example in three dimensions the vectors (v0, v1, v2, v3) are the vertices of a 3-simplex or tetrahedron. Write these as
Choose the first vector v0 to have all but the first component zero, so by the first property it must be (1, 0, 0) and the vectors become
By the second property the dot product of v0 with all other vectors is -, so each of their x components must equal this, and the vectors become
Next choose v1 to have all but the first two elements zero. The second element is the only unknown. It can be calculated from the first property using the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
(choose any of the two square roots), and so the second vector can be completed:
The second property can be used to calculate the remaining y components, by taking the dot product of v1 with each and solving to give
From which the z components can be calculated, using the Pythagorean theorem again to satisfy the first property, the two possible square roots giving the two results
This process can be carried out in any dimension, using n + 1 vectors, applying the first and second properties alternately to determine all the values.
Geometric properties
The oriented volumeVolume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of an n-simplex in n-dimensional space with vertices (v0, ..., vn) is
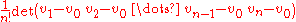
where each column of the n × n determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
is the difference between the vectors representing two vertices. Without the 1/n! it is the formula for the volume of an n-parallelepiped
Parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
. One way to understand the 1/n! factor is as follows. If the coordinates of a point in a unit n-box are sorted, together with 0 and 1, and successive differences are taken, then since the results add to one, the result is a point in an n simplex spanned by the origin and the closest n vertices of the box. The taking of differences was a unimodular (volume-preserving) transformation, but sorting compressed the space by a factor of n!.
The volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
under a standard n-simplex (i.e. between the origin and the simplex in Rn+1) is
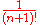
The volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of a regular n-simplex with unit side length is

as can be seen by multiplying the previous formula by xn+1, to get the volume under the n-simplex as a function of its vertex distance x from the origin, differentiating with respect to x, at
 (where the n-simplex side length is 1), and normalizing by the length
(where the n-simplex side length is 1), and normalizing by the length  of the increment,
of the increment,  , along the normal vector.
, along the normal vector.The dihedral angle
Dihedral angle
In geometry, a dihedral or torsion angle is the angle between two planes.The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection...
of a regular n-dimensional simplex is cos−1(1/n).
Simplexes with an "orthogonal corner"
Orthogonal corner means here, that there is a vertex at which all adjacent hyperfaces are pairwise orthogonal. Such simplexes are generalizations of right angle triangles and for them there exists a n-dimensional version of the Pythagorean theoremPythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
:
The sum of the squared (n-1)-dimensional volumes of the hyperfaces adjacent to the orthogonal corner equals the squared (n-1)-dimensional volume of the hyperface opposite of the orthogonal corner.
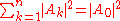
where
 are hyperfaces being pairwise orthogonal to each other but not orthogonal to
are hyperfaces being pairwise orthogonal to each other but not orthogonal to 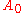 , which is the hyperface opposite of the orthogonal corner.
, which is the hyperface opposite of the orthogonal corner.For a 2-simplex the theorem is the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
for triangles with a right angle and for a 3-simplex it is de Gua's theorem for a tetrahedron
with a cube corner.
Relation to the (n+1)-hypercube
The Hasse diagramHasse diagram
In order theory, a branch of mathematics, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction...
of the face lattice of an n-simplex is isomorphic to the graph of the (n+1)-hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
's edges, with the hypercube's vertices mapping to each of the n-simplex's elements, including the entire simplex and the null polytope as the extreme points of the lattice (mapped to two opposite vertices on the hypercube). This fact may be used to efficiently enumerate the simplex's face lattice, since more general face lattice enumeration algorithms are more computationally expensive.
The n-simplex is also the vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
of the (n+1)-hypercube. It is also the facet of the (n+1)-orthoplex.
Topology
TopologicallyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, an n-simplex is equivalent to an n-ball
Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
. Every n-simplex is an n-dimensional manifold with boundary.
Probability
In probability theory, the points of the standard n-simplex in -space are the space of possible parameters (probabilities) of the categorical distribution
-space are the space of possible parameters (probabilities) of the categorical distributionCategorical distribution
In probability theory and statistics, a categorical distribution is a probability distribution that describes the result of a random event that can take on one of K possible outcomes, with the probability of each outcome separately specified...
on n+1 possible outcomes.
Algebraic topology
In algebraic topologyAlgebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, simplices are used as building blocks to construct an interesting class of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s called simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
es. These spaces are built from simplices glued together in a combinatorial
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
fashion. Simplicial complexes are used to define a certain kind of homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
called simplicial homology
Simplicial homology
In mathematics, in the area of algebraic topology, simplicial homology is a theory with a finitary definition, and is probably the most tangible variant of homology theory....
.
A finite set of k-simplexes embedded in an open subset of Rn is called an affine k-chain. The simplexes in a chain need not be unique; they may occur with multiplicity
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
. Rather than using standard set notation to denote an affine chain, it is instead the standard practice to use plus signs to separate each member in the set. If some of the simplexes have the opposite orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
, these are prefixed by a minus sign. If some of the simplexes occur in the set more than once, these are prefixed with an integer count. Thus, an affine chain takes the symbolic form of a sum with integer coefficients.
Note that each face of an n-simplex is an affine n-1-simplex, and thus the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of an n-simplex is an affine n-1-chain. Thus, if we denote one positively-oriented affine simplex as
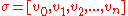
with the
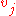 denoting the vertices, then the boundary
denoting the vertices, then the boundary  of σ is the chain
of σ is the chain .
.More generally, a simplex (and a chain) can be embedded into a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
by means of smooth, differentiable map
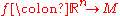 . In this case, both the summation convention for denoting the set, and the boundary operation commute with the embedding. That is,
. In this case, both the summation convention for denoting the set, and the boundary operation commute with the embedding. That is,
where the
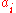 are the integers denoting orientation and multiplicity. For the boundary operator
are the integers denoting orientation and multiplicity. For the boundary operator  , one has:
, one has: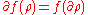
where ρ is a chain. The boundary operation commutes with the mapping because, in the end, the chain is defined as a set and little more, and the set operation always commutes with the map operation
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
(by definition of a map).
A continuous map
 to a topological space
to a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X is frequently referred to as a singular n-simplex.
Applications
Simplices are used in plotting quantities that sum to 1, such as proportions of subpopulations, as in a ternary plotTernary plot
A ternary plot, ternary graph, triangle plot, simplex plot, or de Finetti diagram is a barycentric plot on three variables which sum to a constant. It graphically depicts the ratios of the three variables as positions in an equilateral triangle...
.
In industrial statistics, simplices arise in problem formulation and in algorithmic solution. In the design of bread, the producer must combine yeast, flour, water, sugar, etc. In such mixture
Mixture
In chemistry, a mixture is a material system made up by two or more different substances which are mixed together but are not combined chemically...
s, only the relative proportions of ingredients matters: For an optimal bread mixture, if the flour is doubled then the yeast should be doubled. Such mixture problem are often formulated with normalized constraints, so that the nonnegative components sum to one, in which case the feasible region forms a simplex. The quality of the bread mixtures can be estimated using response surface methodology
Response surface methodology
In statistics, response surface methodology explores the relationships between several explanatory variables and one or more response variables. The method was introduced by G. E. P. Box and K. B. Wilson in 1951. The main idea of RSM is to use a sequence of designed experiments to obtain an...
, and then a local maximum can be computed using a nonlinear programming
Nonlinear programming
In mathematics, nonlinear programming is the process of solving a system of equalities and inequalities, collectively termed constraints, over a set of unknown real variables, along with an objective function to be maximized or minimized, where some of the constraints or the objective function are...
method, such as sequential quadratic programming
Sequential quadratic programming
Sequential quadratic programming is an iterative method for nonlinear optimization. SQP methods are used on problems for which the objective function and the constraints are twice continuously differentiable....
.
In operations research
Operations research
Operations research is an interdisciplinary mathematical science that focuses on the effective use of technology by organizations...
, linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
problems can be solved by the simplex algorithm
Simplex algorithm
In mathematical optimization, Dantzig's simplex algorithm is a popular algorithm for linear programming. The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century....
of George Dantzig
George Dantzig
George Bernard Dantzig was an American mathematical scientist who made important contributions to operations research, computer science, economics, and statistics....
.
In geometric design
Geometric design
Geometric design , also known as geometric modelling, is a branch of computational geometry. It deals with the construction and representation of free-form curves, surfaces, or volumes. Core problems are curve and surface modelling and representation...
and computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, many methods first perform simplicial triangulations of the domain and then fit interpolating
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
polynomials
Polynomial and rational function modeling
In statistical modeling , polynomial functions and rational functions are sometimes used as an empirical technique for curve fitting.-Polynomial function models:A polynomial function is one that has the form...
to each simplex.
See also
- Causal dynamical triangulation
- Distance geometryDistance geometryDistance geometry is the characterization and study of sets of points based only on given values of the distances between member pairs. Therefore distance geometry has immediate relevance where distance values are determined or considered, such as in surveying, cartography and...
- Delaunay triangulationDelaunay triangulationIn mathematics and computational geometry, a Delaunay triangulation for a set P of points in a plane is a triangulation DT such that no point in P is inside the circumcircle of any triangle in DT. Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the...
- Hill tetrahedronHill tetrahedronIn geometry, the Hill tetrahedra are a family of space-filling tetrahedra. They were discovered in 1896 by M.J.M. Hill, a professor of mathematics at the University College London, who showed that they are scissor-congruent to a cube.- Construction :...
- Other regular n-polytopePolytopeIn elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
s- HypercubeHypercubeIn geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
- Cross-polytopeCross-polytopeIn geometry, a cross-polytope, orthoplex, hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of . The cross-polytope is the convex hull of its vertices...
- TesseractTesseractIn geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...
- Hypercube
- PolytopePolytopeIn elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
- Metcalfe's LawMetcalfe's lawMetcalfe's law states that the value of a telecommunications network is proportional to the square of the number of connected usersof the system...
- List of regular polytopes
- Schläfli orthoschemeSchläfli orthoschemeIn geometry, Schläfli orthoscheme is a type of simplex. They are defined by a sequence of edges , , \dots, \, that are mutually orthogonal. These were introduced by Ludwig Schläfli, who called them orthoschemes and studied their volume in the Euclidean, Lobachevsky and the spherical geometry. ...
- Simplex algorithmSimplex algorithmIn mathematical optimization, Dantzig's simplex algorithm is a popular algorithm for linear programming. The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century....
- a method for solving optimisation problems with inequalities. - Simplicial complexSimplicial complexIn mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
- Simplicial homologySimplicial homologyIn mathematics, in the area of algebraic topology, simplicial homology is a theory with a finitary definition, and is probably the most tangible variant of homology theory....
- Simplicial setSimplicial setIn mathematics, a simplicial set is a construction in categorical homotopy theory which is a purely algebraic model of the notion of a "well-behaved" topological space...
- Ternary plotTernary plotA ternary plot, ternary graph, triangle plot, simplex plot, or de Finetti diagram is a barycentric plot on three variables which sum to a constant. It graphically depicts the ratios of the three variables as positions in an equilateral triangle...
- 3-sphere3-sphereIn mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...







