
Lebesgue integration
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Lebesgue integration, named after French
France
The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Henri Lebesgue
Henri Lebesgue
Henri Léon Lebesgue was a French mathematician most famous for his theory of integration, which was a generalization of the seventeenth century concept of integration—summing the area between an axis and the curve of a function defined for that axis...
(1875-1941), refers to both the general theory of integration
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
with respect to a general measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
, and to the specific case of integration of a function defined on a subset of the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
or a higher dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
with respect to the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
. This article focuses on the more general concept.
Lebesgue integration plays an important role in real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
, the axiomatic theory of probability
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, and many other fields in the mathematical sciences.
The integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of a non-negative function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
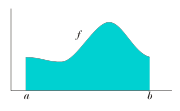
can be regarded in the simplest case as the area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
between the graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of that function and the x-axis. The Lebesgue integral is a construction that extends the integral to a larger class of functions defined over spaces more general than the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
.
For non-negative functions with a smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
enough graph (such as continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
functions on closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
bounded
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
s), the area under the curve is defined as the integral and computed using techniques of approximation of the region by polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
s (see Simpson's rule
Simpson's rule
In numerical analysis, Simpson's rule is a method for numerical integration, the numerical approximation of definite integrals. Specifically, it is the following approximation:...
). For more irregular functions (such as the limiting
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
processes of mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
and probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
), better approximation techniques are required in order to define a suitable integral.
Introduction
The integral of a function f between limits a and b can be interpreted as the area under the graph of f. This is easy to understand for familiar functions such as polynomials, but what does it mean for more exotic functions? In general, what is the class of functions for which "area under the curve" makes sense? The answer to this question has great theoretical and practical importance.As part of a general movement toward rigour in mathematics in the nineteenth century, attempts were made to put the integral calculus on a firm foundation. The Riemann integral
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
, proposed by Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
(1826–1866), is a broadly successful attempt to provide such a foundation. Riemann's definition starts with the construction of a sequence of easily-calculated areas which converge to the integral of a given function. This definition is successful in the sense that it gives the expected answer for many already-solved problems,
and gives useful results for many other problems.
However, Riemann integration does not interact well with taking limits of sequences of functions, making such limiting processes difficult to analyze. This is of prime importance, for instance, in the study of Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
, Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
s and other topics. The Lebesgue integral is better able to describe how and when it is possible to take limits under the integral sign. The Lebesgue definition considers a different class of easily-calculated areas than the Riemann definition, which is the main reason the Lebesgue integral is better behaved.
The Lebesgue definition also makes it possible to calculate integrals for a broader class of functions.
For example, the Dirichlet function, which is 0 where its argument is irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
and 1 otherwise, has a Lebesgue integral, but it does not have a Riemann integral.
Construction of the Lebesgue integral
The discussion that follows parallels the most common expository approach to the Lebesgue integral. In this approach, the theory of integration has two distinct parts:- A theory of measurable sets and measures on these sets.
- A theory of measurable functions and integrals on these functions.
Measure theory
Measure theory was initially created to provide a useful abstraction of the notion of length of subsets of the real line and, more generally, area and volume of subsets of Euclidean spaces. In particular, it provided a systematic answer to the question of which subsets of R have a length. As was shown by later developments in set theorySet theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
(see non-measurable set
Non-measurable set
In mathematics, a non-measurable set is a set whose structure is so complicated that it cannot be assigned any meaningful measure. Such sets are constructed to shed light on the notions of length, area and volume in formal set theory....
), it is actually impossible to assign a length to all subsets of R in a way which preserves some natural additivity and translation invariance properties. This suggests that picking out a suitable class of measurable subsets is an essential prerequisite.
The Riemann integral uses the notion of length explicitly. Indeed, the element of calculation for the Riemann integral is the rectangle [a, b] × [c, d], whose area is calculated to be (b − a)(d − c). The quantity b − a is the length of the base of the rectangle and d − c is the height of the rectangle. Riemann could only use planar rectangles to approximate the area under the curve because there was no adequate theory for measuring more general sets.
In the development of the theory in most modern textbooks (after 1950), the approach to measure and integration is axiomatic. This means that a measure is any function μ defined on a certain class X of subsets of a set E, which satisfies a certain list of properties. These properties can be shown to hold in many different cases.
Integration
We start with a measure space (E, X, μ) where E is a set, X is a σ-algebraSigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
of subsets of E and μ is a (non-negative
Signed measure
In mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
) measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on E, defined on the sets of X.
For example, E can be Euclidean n-space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn or some Lebesgue measurable
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
subset of it, X will be the σ-algebra of all Lebesgue measurable subsets of E, and μ will be the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
. In the mathematical theory of probability, we confine our study to a probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
measure μ, which satisfies
 .
.In Lebesgue's theory, integrals are defined for a class of functions called measurable function
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
s. A function ƒ is measurable if the pre-image of every closed interval is in X:

It can be shown that this is equivalent to requiring that the pre-image of any Borel
Borel algebra
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
subset of R be in X. We will make this assumption henceforth. The set of measurable functions is closed under algebraic operations, but more importantly the class is closed under various kinds of pointwise sequential limits
Limit superior and limit inferior
In mathematics, the limit inferior and limit superior of a sequence can be thought of as limiting bounds on the sequence...
:
are measurable if the original sequence (ƒk)k, where k ∈ N, consists of measurable functions.
We build up an integral
for measurable real-valued functions ƒ defined on E in stages:
Indicator functions: To assign a value to the integral of the indicator function
 of a measurable set S consistent with the given measure μ, the only reasonable choice is to set:
of a measurable set S consistent with the given measure μ, the only reasonable choice is to set:
Notice that the result may be equal to +∞, unless μ is a finite measure.
Simple functions: A finite linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of indicator functions

where the coefficients ak are real numbers and the sets Sk are measurable, is called a measurable simple function
Simple function
In the mathematical field of real analysis, a simple function is a real-valued function over a subset of the real line which attains only a finite number of values...
. We extend the integral by linearity to non-negative measurable simple functions. When the coefficients ak are non-negative, we set

The convention 0 × ∞ = 0 must be used, and the result may be infinite. Even if a simple function can be written in many ways as a linear combination of indicator functions, the integral will always be the same; this can be shown using the additivity property of measures.
Some care is needed when defining the integral of a real-valued simple function, in order to avoid the undefined expression ∞ − ∞: one assumes that the representation

is such that μ(Sk) < ∞ whenever ak ≠ 0. Then the above formula for the integral of ƒ makes sense, and the result does not depend upon the particular representation of ƒ satisfying the assumptions.
If B is a measurable subset of E and s a measurable simple function one defines

Non-negative functions: Let ƒ be a non-negative measurable function on E which we allow to attain the value +∞, in other words, ƒ takes non-negative values in the extended real number line
Extended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
. We define

We need to show this integral coincides with the preceding one, defined on the set of simple functions. When E is a segment [a, b], there is also the question of whether this corresponds in any way to a Riemann notion of integration. It is possible to prove that the answer to both questions is yes.
We have defined the integral of ƒ for any non-negative extended real-valued measurable function on E. For some functions, this integral ∫E ƒ dμ will be infinite.
Signed functions: To handle signed functions, we need a few more definitions. If ƒ is a measurable function of the set E to the reals (including ± ∞), then we can write

where


Note that both ƒ+ and ƒ− are non-negative measurable functions. Also note that

We say that the Lebesgue integral of the measurable function
 exists, or is defined if at least one of
exists, or is defined if at least one of  and
and  is finite:
is finite:
In this case we define

If

we say that ƒ is Lebesgue integrable.
It turns out that this definition gives the desirable properties of the integral.
Complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
valued functions can be similarly integrated, by considering the real part and the imaginary part separately.
Intuitive interpretation
To get some intuition about the different approaches to integration, let us imagine that it is desired to find a mountain's volume (above sea level).The Riemann-Darboux approach: Divide the base of the mountain into a grid of 1 meter squares. Measure the altitude of the mountain at the center of each square. The volume on a single grid square is approximately 1x1x(altitude), so the total volume is the sum of the altitudes.
The Lebesgue approach: Draw a contour map of the mountain, where each contour is 1 meter of altitude apart. The volume of earth contained in a single contour is approximately that contour's area times its height. So the total volume is the sum of these volumes.
Folland summarizes the difference between the Riemann and Lebesgue approaches thus: "to compute the Riemann integral of f, one partitions the domain [a, b] into subintervals", while in the Lebesgue integral, "one is in effect partitioning the range of f".
See also Properties of simple functions.
Example
Consider the indicator function of the rational numbers, 1Q. This function is nowhere continuousNowhere continuous
In mathematics, a nowhere continuous function, also called an everywhere discontinuous function, is a function that is not continuous at any point of its domain...
.
-
 is not Riemann-integrable on [0,1]: No matter how the set [0,1] is partitioned into subintervals, each partition will contain at least one rational and at least one irrational number, since rationals and irrationals are both dense in the reals. Thus the upper Darboux sums will all be one, and the lower Darboux sums will all be zero.
is not Riemann-integrable on [0,1]: No matter how the set [0,1] is partitioned into subintervals, each partition will contain at least one rational and at least one irrational number, since rationals and irrationals are both dense in the reals. Thus the upper Darboux sums will all be one, and the lower Darboux sums will all be zero.
-
 is Lebesgue-integrable on [0,1] using the Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
is Lebesgue-integrable on [0,1] using the Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
: Indeed it is the indicator function of the rationals so by definition
- since
 is countable.
is countable.
Domain of integration
A technical issue in Lebesgue integration is that the domain of integration is defined as a set (a subset of a measure space), with no notion of orientation. In elementary calculus, one defines integration with respect to an orientation: Generalizing this to higher dimensions yields integration of differential form
Generalizing this to higher dimensions yields integration of differential formDifferential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s. By contrast, Lebesgue integration provides an alternative generalization, integrating over subsets with respect to a measure; this can be notated as
 to indicate integration over a subset A. For details on the relation between these generalizations, see Differential form: Relation with measures.
to indicate integration over a subset A. For details on the relation between these generalizations, see Differential form: Relation with measures.Limitations of the Riemann integral
Here we discuss the limitations of the Riemann integral and the greater scope offered by the Lebesgue integral. We presume a working understanding of the Riemann integralRiemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
.
With the advent of Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
, many analytical problems involving integrals came up whose satisfactory solution required interchanging limit processes and integral signs. However, the conditions under which the integrals
-
 and
and 
are equal proved quite elusive in the Riemann framework. There are some other technical difficulties with the Riemann integral.
These are linked with the limit-taking difficulty discussed above.
Failure of monotone convergence. As shown above, the indicator function 1Q on the rationals is not Riemann integrable. In particular, the Monotone convergence theorem fails. To see why, let {ak} be an enumeration of all the rational numbers in [0,1] (they are countable so this can be done.) Then let

The function gk is zero everywhere except on a finite set of points, hence its Riemann integral is zero. The sequence gk is also clearly non-negative and monotonically increasing to 1Q, which is not Riemann integrable.
Unsuitability for unbounded intervals. The Riemann integral can only integrate functions on a bounded interval. It can however be extended to unbounded intervals by taking limits, so long as this doesn't yield an answer such as
 .
.Integrating on structures other than Euclidean space. The Riemann integral is inextricably linked to the order structure of the line.
Basic theorems of the Lebesgue integral
The Lebesgue integral does not distinguish between functions which differ only on a set of μ-measure zero. To make this precise, functions f and g are said to be equal almost everywhereAlmost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
(a.e.) if

- If f, g are non-negative measurable functions (possibly assuming the value +∞) such that f = g almost everywhere, then

To wit, the integral respects the equivalence relation of almost-everywhere equality.
- If f, g are functions such that f = g almost everywhere, then f is Lebesgue integrable if and only if g is Lebesgue integrable and the integrals of f and g are the same.
The Lebesgue integral has the following properties:
Linearity
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
: If f and g are Lebesgue integrable functions and a and b are real numbers, then af + bg is Lebesgue integrable and

Monotonicity: If f ≤ g, then

Monotone convergence theorem: Suppose {fk}k ∈ N is a sequence of non-negative measurable functions such that

Then

Note: The value of any of the integrals is allowed to be infinite.
Fatou's lemma
Fatou's lemma
In mathematics, Fatou's lemma establishes an inequality relating the integral of the limit inferior of a sequence of functions to the limit inferior of integrals of these functions...
: If {fk}k ∈ N is a sequence of non-negative measurable functions, then

Again, the value of any of the integrals may be infinite.
Dominated convergence theorem
Dominated convergence theorem
In measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which two limit processes commute, namely Lebesgue integration and almost everywhere convergence of a sequence of functions...
: If {fk}k ∈ N is a sequence of complex measurable functions with pointwise limit f, and if there is a Lebesgue integrable function g (i.e., g belongs to the space L1
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
) such that |fk| ≤ g for all k, then f is Lebesgue integrable and

Proof techniques
To illustrate some of the proof techniques used in Lebesgue integration theory, we sketch a proof of the above mentioned Lebesgue monotone convergence theorem. Let {fk}k ∈ N be a non-decreasing sequence of non-negative measurable functions and put
By the monotonicity property of the integral, it is immediate that:
and the limit on the right exists, since the sequence is monotonic.
We now prove the inequality in the other direction. It follows from the definition of integral that there is a non-decreasing sequence (gn) of non-negative simple functions such that gn ≤ f and

Therefore, it suffices to prove that for each n ∈ N,

We will show that if g is a simple function and

almost everywhere, then

By breaking up the function g into its constant value parts, this reduces to the case in which g is the indicator function of a set. The result we have to prove is then
- Suppose A is a measurable set and {fk}k ∈ N is a nondecreasing sequence of non-negative measurable functions on E such that
- for almost all x ∈ A. Then
To prove this result, fix ε > 0 and define the sequence of measurable sets

By monotonicity of the integral, it follows that for any
k ∈ N,

Because almost every x will be in Bk for large enough k, we have

up to a set of measure 0. Thus by countable additivity of μ, and since Bk increases with k,

As this is true for any positive ε the result follows.
Alternative formulations
It is possible to develop the integral with respect to the Lebesgue measure without relying on the full machinery of measure theory. One such approach is provided by Daniell integralDaniell integral
In mathematics, the Daniell integral is a type of integration that generalizes the concept of more elementary versions such as the Riemann integral to which students are typically first introduced...
.
There is also an alternative approach to developing the theory of integration via methods of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
. The Riemann integral exists for any continuous function f of compact support
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
defined on Rn (or a fixed open subset). Integrals of more general functions can be built starting from these integrals.
Let Cc be the space of all real-valued compactly supported continuous functions of R. Define a norm on Cc by
Then Cc is a normed vector space (and in particular, it is a metric space.) All metric spaces have Hausdorff completions
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
, so let L1 be its completion. This space is isomorphic to the space of Lebesgue integrable functions modulo the subspace of functions with integral zero. Furthermore, the Riemann integral ∫ is a uniformly continuous functional with respect to the norm on Cc, which is dense in L1. Hence ∫ has a unique extension to all of L1. This integral is precisely the Lebesgue integral.
This approach can be generalised to build the theory of integration with respect to Radon measure
Radon measure
In mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
s on locally compact space
Locally compact space
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
s. It is the approach adopted by Bourbaki (2004); for more details see Radon measures on locally compact spaces.
See also
- Henri Lebesgue, for a non-technical description of Lebesgue integration
- null setNull setIn mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
- integrationIntegralIntegration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
- measureMeasure (mathematics)In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
- sigma-algebraSigma-algebraIn mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
- Lebesgue space
- Lebesgue-Stieltjes integrationLebesgue-Stieltjes integrationIn measure-theoretic analysis and related branches of mathematics, Lebesgue–Stieltjes integration generalizes Riemann–Stieltjes and Lebesgue integration, preserving the many advantages of the former in a more general measure-theoretic framework...
- Henstock-Kurzweil integralHenstock-Kurzweil integralIn mathematics, the Henstock–Kurzweil integral, also known as the Denjoy integral and the Perron integral, is one of a number of definitions of the integral of a function. It is a generalization of the Riemann integral which in some situations is more useful than the Lebesgue integral.This integral...








